基于遗传算法的电动汽车充电站选址定容研究

彭国财，邓玉珍，张 邻

（1.南昌航空大学经济管理学院，江西南昌；2.南昌航空大学土木建筑学院，江西南昌）

引言

根据公安部发布的最新数据显示，截至2023 年6月底，我国新能源汽车保有量达1 620 万辆; 截至2022 年末，中国累计充电桩数量达521 万台，同比增长率为99.08%，创历史新高。得益于政策扶持、技术研发和市场推广的进程加速，中国新能源车市持续维持高增长的态势，已经成为国内车市最大亮点。

尽管我国电动汽车充电站建设正处于快速发展阶段，但目前仍缺乏科学规范的充电站选址和定容原则。依赖于概括性的建设原则和实际经验来指导充电站建设，可能导致充电站的利用率下降，浪费公共资源的问题仍然存在。

在电动汽车选址规划的问题上，已有许多学者展开了研究。在文献[1]中，作者考虑到用户之间的竞争关系，提出了一种博弈选址模型。该模型考虑充电站的排队情况，以确保用户能够得到满意的充电服务。文献[2]从可行性原则的角度出发，重点考虑充电站选址方案的地理环境和社会环境建设的可行性。文献[3]在选址过程中，提出应该避免选择那些存在防洪条件较差、地震多发等自然灾害风险较高的区域。文献[4]在致力于降低配电网网络损耗的前提下，对充电站的选址建设进行了合理规划。文献[5]考虑了各充电站之间的相互影响，提出了改进型p-中心模型，能够满足城市内各类型电动汽车的充电需求。

本文以最小化电动汽车充电站投资建设成本为切入点，结合道路交通流量，考虑充电站对路网中的充电需求的最大覆盖，建立选址优化模型，在满足用户充电需求的同时，降低充电站的投资建设成本。

1 充电站建设成本模型

电动汽车充电站的建造并投入商业运行，其总成本通常包括土地使用成本、设备采购成本和运行维护成本。

1.1 土地使用成本

建造充电站需要占用土地。土地的位置、面积和市场需求将对费用产生影响。令第i 个电动汽车充电站候选址的土地总成本为 θi，充电站投资使用年限为ni，则第i 个电动汽车充电站候选址的土地使用年成本可表示为：

式中：r 为贴现率。

1.2 设备成本

电动汽车充电站的设备购买成本包括购买和安装充电桩、充电设备以及配套的变压器等设备所需的费用。第i 个电动汽车充电站候选址的设备购买年成本表示如下：

式中：wi为第i 个候选址购买的充电桩数量；k1为单个充电桩的购买成本；gi为第i 个候选址购买的变压器数量；k2为单个变压器的购买成本。

1.3 运行维护成本

充电站的运行维护成本是指为保持充电站正常运营所需的费用，其中包括工作人员工资待遇，设备折旧及维护成本。通常情况下，充电站的运行维护支出不明确，本文以充电站设备购买成本的百分比进行计算。因此，则第i 个电动汽车充电站候选址的运行维护年成本可表示为：

因此，选择在第i 个候选址建立电动汽车充电站，其年总成本ci可表示如下：

综上所述，最小化电动汽车建设成本的目标函数如下：

式中：xi为0-1 变量，当选择在第i 个候选址建立电动汽车充电站时，xi=1，否则xi=0。

2 最大需求量覆盖模型

2.1 确定电动汽车充电需求

令第i 个电动汽车充电站候选址覆盖的路口节点的集合为Di。任意路口节点j∈Di，与节点j 相连的第m 条路段的日交通流量为qjm，则路口节点j 的日交通流量qj可表示为：

若电动汽车渗透率（电动汽车占比）为 β，电动汽车的充电概率为 λ，则路口节点j 的日充电需求量sj可表示为：

2.2 充电站定容

充电桩作为电动汽车与充电站的连接中介，其配置数量决定了充电站的服务能力。若第i 个电动汽车充电站候选址配置有hi个充电桩，充电站i 的服务能力为li，不妨令服务能力li为充电桩数量hi的函数，即：

充电站的建设应满足其覆盖区域的电动汽车充电需求，表示如下：

式中：yji为节点j 的需求中被分配到充电站i 的比例；li为决策变量，表示充电站i 的服务能力。

3 约束条件

式中：M 为足够大的数。

（2） 充电站i 的充电桩配置数量应为整数，且不能超过充电站的最大配置限制。

4 算法实现与算例分析

上述问题具有多约束、非线性的特点，传统方法难以获得全局最优解，本文采取遗传算法对上述问题进行求解。设计算法如下：

Step1：初始化数据。输入路口节点车流量数据、充电站候选址相关数据等。

Step2：初始化种群。i=1，生成初始种群Ni，种群中的个体表示一个电动汽车充电站的配置方案，包括选址位置、服务能力、变压器配置等信息。

Step3：适应度评估。根据目标函数对每个个体进行评估，计算其适应度值。

Step4：选择操作。对种群适应度值排序，选择一部分优秀的个体作为父代。

Step5：交叉、变异操作。通过交叉操作，随机选择两个父代个体生成子代个体，对部分子代个体进行变异操作，增加种群的多样性。

Step6：替换操作。i:=i+1，将父代和子代进行排序，选择优秀个体形成新的种群Ni。

Step7：判断是否到达最大迭代次数，i≥？是，转入Step8；否，则转入Step3。

Step8：输出充电站最优选址配置信息。

城市某规划区域面积为25 km2，共有路口节点35 个，区域路网如图1 所示。

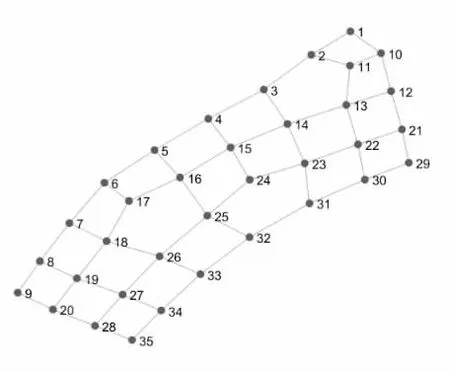
图1 区域路网示意

遗传算法参数设置如下：种群规模为50，最大迭代次数为40，个体交叉概率为0.8，变异概率为0.05。使用Matlab2021a 进行求解。根据遗传算法优化结果，若覆盖规划区域内所有路口节点的电动汽车充电需求，电动汽车充电站的最小建设年成本为276.3 万元，此时，共建设8 个充电站，共配置88 个充电桩。算法迭代如图2 所示。充电站选址及节点覆盖如图3 所示。最优方案下的年总成本如表1 所示。充电站充电桩配置数量及覆盖节点如表2 所示。

表1 最优方案下的年总成本（单位：万元）

表2 充电站充电桩配置数量及覆盖节点

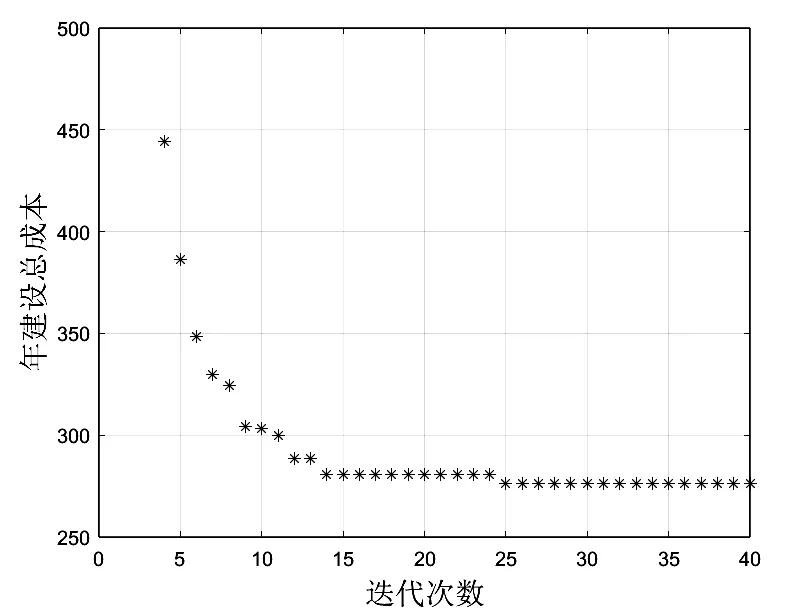
图2 算法迭代

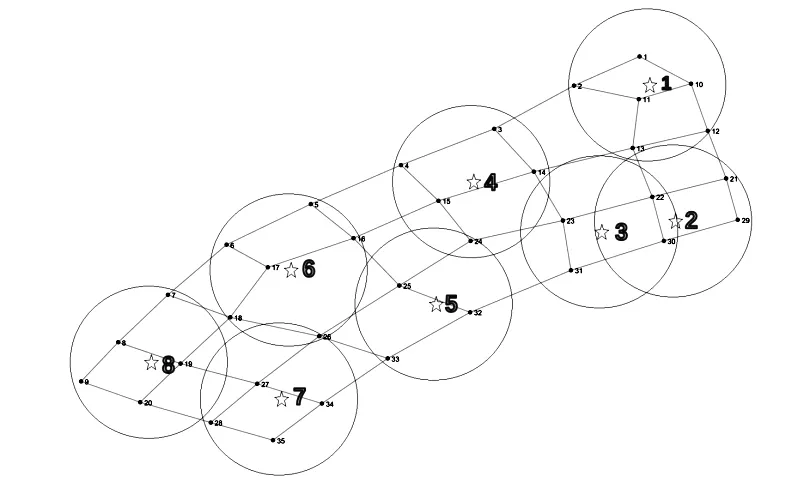
图3 充电站选址方案

5 结论

本文提出基于遗传算法的电动汽车充电站选址定容研究，以最小化建设成本和最大化需求覆盖为目标，旨在寻找最优的电动汽车充电站选址及配置方案。首先建立了充电站建设成本模型，包括土地使用成本、设备购买成本和运行维护成本。其次，通过确定充电需求量和充电站的服务能力，形成最大需求量覆盖模型。最后，采用遗传算法对该问题进行求解，并给出了算例分析结果。通过算例分析，得到了最优的充电站选址和充电桩配置方案。最小建设成本为276.3 万元，共建设8 个充电站，并配置了88 个充电桩。算法收敛曲线显示算法在40 次迭代内得到了最优解。