模体超网络的构建方法及其特性分析

董浩然，张 科,2，胡文军,2

(1.湖州师范学院信息工程学院，浙江湖州；2.浙江省现代农业资源智慧管理与应用研究重点实验室，浙江湖州)

引言

复杂网络中常常将现实世界的事物抽象成网络系统中的节点，而事物之间的联系抽象为节点之间的连边。在基于普通图的复杂网络研究中，研究者们研究了许多复杂网络模型以便于揭示网络的性质。Berge[1]在1989 年首次提出了超图一词，并且定义了无向超图。之后Estrada[2]认为凡是可以用超图表示的网络即为超网络（Hypernetwork）。超图为普通图的推广为了研究超网络的机制以及性质，研究者们构建了许多基于超图的超网络模型。近年随着人们在研究生态食物网、大肠杆菌和酿酒酵母遗传网络、以及执行信息处理的网络中都发现了一些相互连接且数量明显高于随机网络的连接模式，且不同网络系统中的这种网络基序[3]不同，因此提出了网络模体[4]的概念。在网络模型的研究中确定性模型以及演化模型[5]一直是研究的重点。本文提出了一种由一个确定性普通网络逆向构建超网络的方法，并在几个普通网络数据集上进行了实验同时对于构建的超网络进行了一些拓扑特性分析。

1 超图的部分理论

1.1 超图定义

设超图H=（V,E）其中V=（v1,v2,v3…vn），E=（e1,e2,e3…,em）为两个有限集，集合V 的一个元素为超图的一个顶点集合E 的一个元素为超图H 的一条超边。当与边关联的顶点数目大于2 时，用一个闭合曲线表示包含这些顶点的一条超边。图1 为一个有两条超边四个顶点的超图示意图。

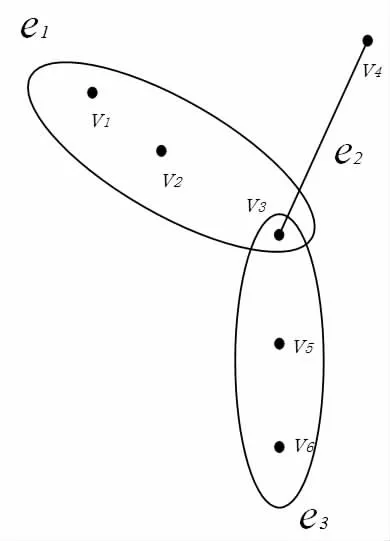
图1 一个有三条超边和6 个顶点的超图

1.2超图的阶、秩

超图H=（V,E）中若两个节点属于同一条超边则称这两个节点邻接或关联。超图H 中的节点个数称为超图的阶。超图H 中的一条超边有最多个顶点邻接则这条超边中包含的节点个数称为该超图的秩。如果超图中每条超边都含有r 个节点则称H 为r 一致超图。

1.3 关联矩阵

对于普通图其数学表达形式就是邻接矩阵，而在超图中超图与其邻接矩阵并不是一对一的关系，而一个超图可以由一个关联矩阵唯一确定，因此我们使用关联矩阵来描述超图。设超图H=（V,E）其关联矩阵B（H）定义为：

1.4节点超度

超图H 中如果节点vi∈ej那么称节点vi与超边ej关联，节点vi的超度定义为所有与vi关联的超边的数目，记为dH（vi）。超图H的度分布定义为：超图H中任取一个节点超度为dH的概率，记为p（dH）。

2 模体超网络构建

2.1 网络模体

许多领域的研究者们都在研究复杂网络。研究人员们发现不同的网络中都会出现一些连接模式相同的子结构，进而有了网络模体这一概念。而模体[6]这一词源于生物学，在生物学中也叫模序，表示蛋白质中具有特定空间构象和特定功能的结构部分。

自然界中许多复杂网络都被证明具有小世界和无标度。的特性。要超越这些全局特征，我们需要了解每一类网络特有的基本元素结构。因此模体反复出现、互连的模式可以推广到网络模型的构建以及研究上。网络中的模体代表了广泛的自然现象。复杂网络系统中的交互作用的重要性也不言而喻，超图作为高阶建模[7]的数学工具也被广泛应用。不同网络的结构的功能性的区别，常体现在局部偏好连接的不同，这时便可以用网络的模体来进行量化。值得说明的是模体的数目是随着模体的阶数呈上升的。以本文研究的无向超网络为例，图2 展示了三阶模体以及四阶模体。

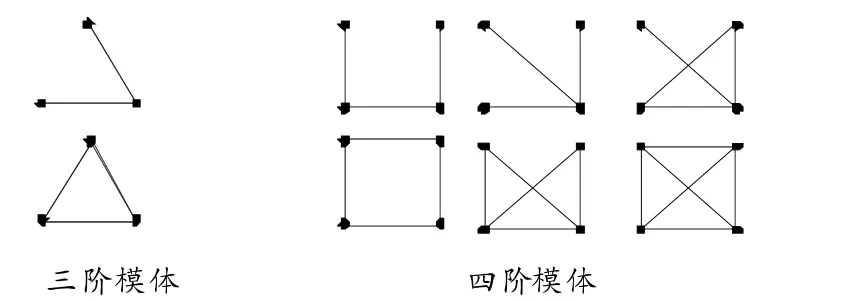
图2 三阶、四阶模体

2.2 超网络构建方法

本文提出了一种由一个确定的普通网络逆向构建的只存在三阶模体的超网络。对于构建完毕的超网络，其网络中的每一条超边都只有三个节点。这类超网络也被称为三一致。具体的构造方法是：首先找到一个连通的普通网络将网络的所有节点和边进行标记并将节点进行编号且将网络中所有的连边放在一个边集中。遍历一遍网络，统计图中所有节点的度，找到所有度大于等于2 的节点。之所以要找出所有度大于等于2 的节点其原因在于三阶模体只有“v”字形和“三角形”两种连接模式，假设一个节点的度等于2 那么意味着在网络中该节点有两个节点与之关联，即存在两个节点与之相连，这时候可以运用复杂网络中聚类系数的概念通过计算该节点的聚类系数则可以判断出与该节点关联的两个节点之间是否存在关联。聚类系数的算法表达式如下：

其中,i 为节点,ei为i 邻节点的关系数，ki为节点的度。这种算法也叫三角形计数法。通过Ci的值可以求出该节点所有三角形的个数。假设Ci等于0，即不存在三角形，由于三阶模体只有两种，那么意味着该节点与其邻居节点为v 字形。如若等于1 那么该节点的邻居节点之间有一条连边，即就是一个三角形。因此在构造超网络时第一遍要对网络中所有度大于等于2的节点去进行构造。对于度大于2 的节点，意味着有多个节点与之存在连边，此时该节点的聚类系数若不为0 意味着存在1 个或多个三角形，三角形个数可以通过聚类系数算法推出。本文提出的算法是优先考虑三角形的情况，即若该节点的邻居节点之间有关联边数m 就存在m 个三角形，将形成该三角形的三个节点以及三条边构造成一条包含三个节点的超边，并从边集中将这三条边标记。之所以要标记用过的连边是为了避免出现重边的情况。在找出所有三角形以后，那么就只剩向该节点添加v 字形，节点的v 字形的数目等于该节点的度取2 的组合数再减去三角形的个数，此时任取两个该节点的邻居节点并将这三个节点构造成一条包含这三个节点的超边。需要特别说明的是在构建超网络模型的过程中会出现一个节点的边被标记的只剩1 条边的情形这时候就跳过这个节点到它的下一个邻居节点直至遍历完所有节点为止。在这里需要用到r- 一致超图的超边数目上下界理论：

其中，n 为网络节点个数，i 为节点度大于等于2 的节点编号，ki为节点度，∂ 为网络中度等于1 且在第一次构造中没有用到的节点个数。

在第一次遍历完所有节点以后此时的超网络可能是连通的也可能是不连通的，如果此时超网络已经连通那么即构建完毕。如果不连通，是因为此时网络中还有度为1 且在第一遍构造中没有包含在超边中的节点。对于这些节点，它的邻居节点的度是大于等于2 的那么只需要从邻居节点的所有连边中任取一条边组成一条v 字形并加入一条超边包含即可。需要补充说明的是在处理这些度为1 节点的时候并不考虑邻居节点的边是否被标记的情形即都当作未标记来处理。最后再判断此时超网络是否连通，如若连通那么超网络模型构造完毕，如若不连通则继续向网络中添加超边直至该超网络连通[8]为止。这里给出超网络的连通算法：

其中，X 为超图的邻接矩阵。图3 展示了构造超网络的过程。

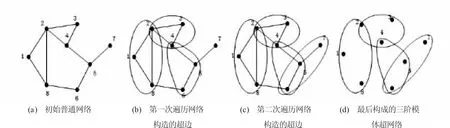
图3 超网络构造过程

2.3 实验分析

为了测试算法的普适性，本文找到了一些具有无标度特性的普通网络数据集依据本文提供的方法对其中的二个网络进行了实验。每个网络仍做十次随机实验，同时统计普通网络的度分布以及生成的超网络的超度分布进行对照。

用Zachary 数据集构建Zachary 网络，该网络有34 个节点以及78 条边。网络中最大的节点度为17，最小的节点度为1。根据我们的算法逆向构建为三阶模体超网络后统计10 次随机生成的超网络的所有超度的数值，其中超度最大值为27，超度最小值为1。从数据统计中我们可以看出，依据普通网络逆向构建的超网络比普通网络拥有更多的度值类型，这不单单是因为10 次实验中每次实验的超度会有不同数值的原因也与我们提出的算法是密切相关的，同时联系实际也符合超网络作为一个描述高阶交互系统的工具的特性。同时逆向构建的超网络也保持了原普通网络的一些特性，构建的超网络仍然具有无标度的特性。

其10 次实验生成的超网络取平均的超度分布与普通网络度分布如图4 所示。

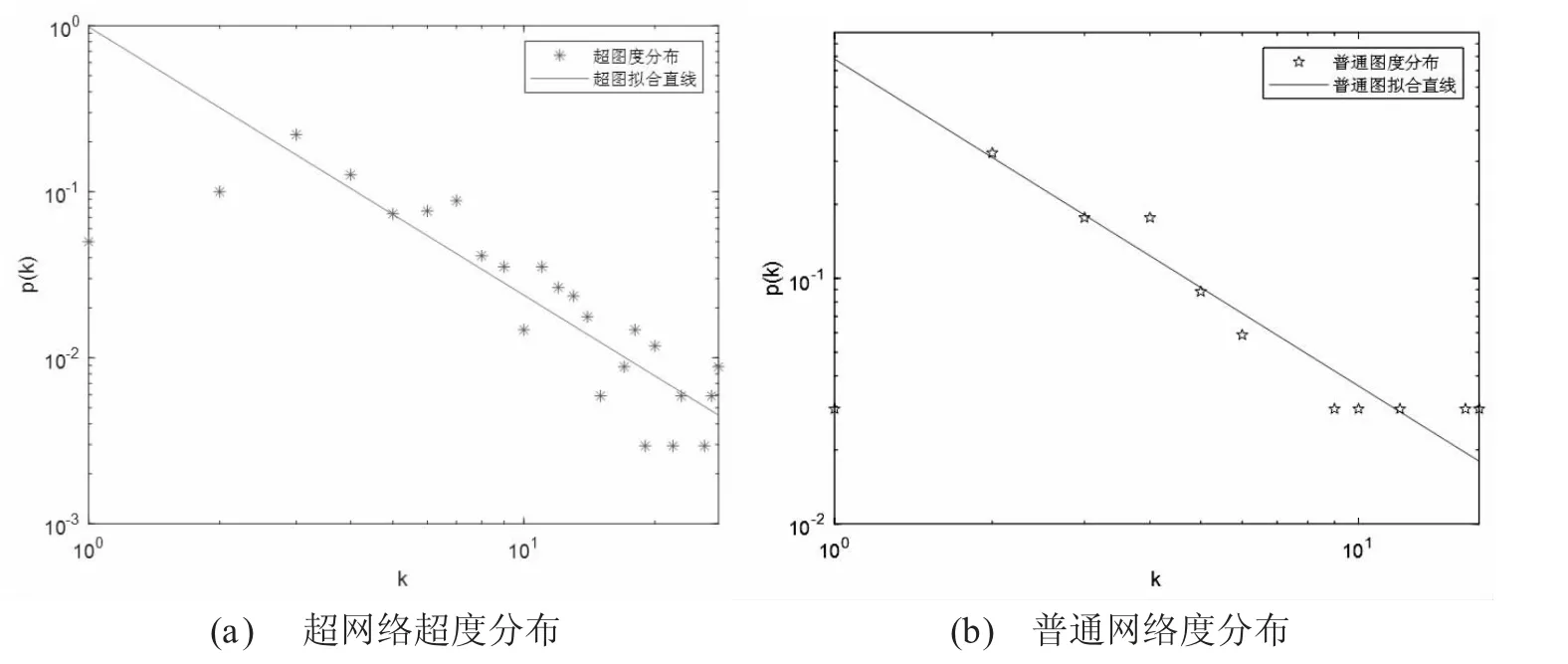
图4 度分布拟合图

结束语

对于超网络模型的研究，往往都是将超网络间接转化为普通网络去进行参照对比，本文通过抓住普通网络中普遍出现的子结构从而将普通网络转化为模体超网络去进行分析对比，进而发现了一些模体超网络的实验结果，而未来四阶模体等更高阶的模体超网络还值得研究者们继续去研究。