区域多源互补发电系统优化配置研究

周华强 常喜强 常春喜

（1.新疆新特晶体硅高科技有限公司 2.国网新疆电力有限公司 3.特变电工新疆新能源股份有限公司）

0 引言

随着煤、石油、天然气等不可再生资源的大量消耗，环境污染等问题的日益严重，以水能、太阳能、风能等可再生能源替代传统能源的形式显得更加严峻和紧迫。但以光伏与风电为代表的可再生能源在发电过程中具有间歇性、波动性和随机性，导致大规模可再生能源集中接入电力系统后，将会对主电网的电能质量和运行稳定性造成严重影响，产生弃风、弃光、甚至脱网等问题[1-2]，在一定程度上将可再生能源变为了不利于并网的“垃圾电”。在此情况下，将具有灵活启停、快速调节等优点的水电，与光伏和风电进行整合协调运行，形成互补关系，是提高可再生能源利用率的一种新的思路[3]。

然而，由于地理位置、天气条件、装机规模等因素，将太阳能、水能和风能整合到一个传统的电力系统中稳定运行并不简单，其发电规模、利用时间等均可能在每月、每天甚至每小时产生很大差异，这要求系统运营商具有很好的灵活性，从而实现新能源发电安全高效利用、系统性减少弃风弃光。而通过对不同能源互补性的分析，可有效帮助系统运营商实现这一目标。根据电力系统设计与研究背景与目标，研究者们通常通过数理统计分析，如皮尔逊相关系数[4-5]，Spearman 相关系数[6]、Kendall 相关系数[7]、图形分析[8]等方法，通过对相关性的分析体现出互补性的强弱，从数学分析的角度呈现各类可再生能源互补利用的可能性，证实多能互补综合利用性能在某种程度上的最优性。

目前世界各国均展开了一些针对多种能源互补性的研究。例如，文献[9]分析了葡萄牙风能、光伏和水能的互补性。文献[10]分析了评估巴西里约热内卢州小型水电站、风电场和光伏的互补潜力，但相关性分析精度仍有提升空间。文献[11]专注于意大利的小型水电站和光伏发电，但其繁琐的计算并不适于大规模的可再生能源系统应用。在中国，文献[12]采用核密度估计方法分别对光伏电站以及风电场的出力概率分布进行计算，并利用Copula 理论对可多能互补电站可靠性进行分析，但该方法并未体现出各类能源各自特性，同时也不适于大规模的可再生能源系统应用。文献[13]对水光互补协调运行及其容量配置进行研究，但未对风电及多能源互补性进行有效分析。

基于现有研究存在的局限性，本文对大规模水电、光伏和风电的互补性进行了研究，并建立了相关性指标，构建了衡量多种能源发电之间互补性强弱的通用表达形式，并以中国青海省黄河上游地区为目标，验证了该方法的有效性，对日后大规模可再生能源互补利用提供了新的着力点。

1 相关性研究

统计学常用相关系数包括Pearson 相关系数、Spearman 相关系数和Kendall 相关系数等[14]。相关系数是一种可以有效反映变量相互关联性的计量值，能够刻画两个变量同时所具有的某种相关程度。相关系数r取值范围通常为[-1，1]，相似度关系为[15]：

将相关性分析引入至可再生能源发电研究中，可以发现，若两类电源出力相关系数越接近1，则这两类能源具有强相关性，其出力大小与时间变化趋势相似，几乎没有互补利用的可能性。若两类电源出力相关系数越接近0，则这两类能源具有弱相关性，证明其出力大小与时间的变化趋势不相同，则证明其在时间尺度上具有一定的互补可能。因此，通过对不同能源出力相关性的研究，可以从侧面反映出能源之间互补性的强弱。

1）Pearson 相关系数法是最为常用的分析相关性的方法[16]，通常是基于数据均值、协方差和标准差计算得出的，因此很容易实现。其计算公式为：

式中，xi，yi为第i个数据的值；为数据的平均值。

2）Spearman 相关系数又称秩相关系数或顺序相关系数[17]，一般用于评估两组变量之间的单调关系。其定义为：

3）Kendall 相关系数根据2 个随机变量间序对的协同一致性来判断其相关性[18]，其定义为：

式中，C为变量x，y中一致性元素的对数；D为不一致性元素的对数；N为样本数目，N1，N2为指向不同变量中拥有相同元素的小集合个数。

由这三种相关系数特性可知，Spearman 相关系数一般用于评估两组数据间单调关系，在计算中会对数据进行重新排列分布，在能源出力相关性的研究中会无法正确反映实际的相关性，影响结果的准确性。Kendall 相关系数主要对变量取值集合中相同元素分别组合成的小集合个数进行分析，无法正确反映出不同能源出力随时间变化的相关性。因此，本文选取更加直观的Pearson 相关系数对各类能源出力相关性进行分析。

2 改进Pearson 相关系数算法

由于均值在统计学中较适用于呈对称分布的数据，且容易受到极端值的影响，导致传统的Pearson系数法只对呈正态分布或接近正态分布的数据集有效，当变量不服从正态分布时，相关系数有相当大的偏差，并且容易受到数据异常点的影响。同时，传统Pearson 相关系数容易过分地放大或缩小用户间的真实相似性，它对数据的绝对数值并不敏感，只能描述数据的变化趋势。

在此情况下，本文运用了一种融合了差异因子的加权Pearson 相关系数计算方法[19]，该方法能有效解决Pearson 相关系数对绝对数值不敏感及易受极端值影响的问题。

1）假定参与Pearson 相关系数计算的两组数据分别为P1={P11，P12，P13，…，P1n}，P2={P21，P22，P23，…，P2n}，将P1和P2的数据差异d（P1，P2）定义为：

2）利用欧几里得定理衡量两个对象之间的距离，计算P1和P2之间的数据差异度：

3）由于数据的数量n也会对数据的相似度产生影响：n越大，相似度越高。所以加入1/n作为权重，新的差异度公式为：

4）归一化处理。为了解决相似度计算中对数据绝对数值不敏感及极端值的问题，本文采用指数函数对dif（P1，P2）做归一化操作，归一化后差异度的取值范围为[0，1]，归一化操作后，dif（P1，P2）可更加精确地修正传统Pearson 相关系数计算。最终差异度为：

5）改进后融合了差异因子的Pearson 相关系数计算公式为：

3 功率建模

本节只考虑基于太阳能光伏、风能和水电的混合能源，描述了由时间序列获得的光伏、风电、水电功率，假设每个地区都是自治的，没有与邻近地区的能源交互。

3.1 光伏模型

光伏发电的输出功率与太阳光照强度呈近似线性相关关系，假定光伏元件按最大功率输出，则输出功率PPV 计算为：

式中，PPV为光伏电源的输出功率；r为标准额定条件；Gr为太阳辐照度，其值为1.0kW/m2；Tr为光伏电池表面温度，一般认为是25℃；G为实际光照辐射强度；Gr为在标准额定条件下的太阳光辐照度，通常取为1000W/m2；αT为功率相对于温度的特征系数；T为光伏电池实际的表面温度；Pr为标准额定条件下光伏电池板的额定输出功率。

3.2 风电模型

风力发电的日发电量通常是按照当天的风速情况所对应各种风力发电机的实际发电功率来计算的，输出功率PW计算为：

式中，PW为风电输出功率；v为风力机轮毂高度处的风速；vi为切入风速；vo为切出风速；vr为额定风速；Pr为额定输出功率。

3.3 水电模型

通常认为，水电功率是由河流流量降落的势能经过水轮机完成能量转换产生的，输出功率Ph见式（13）。相比于光伏与风电，水电具有启停方便、调节快速等优点，当与光伏或风电一起运行时，可有效改善光伏与风电的波动、随机性出力，获得平稳、可靠的电能：

式中，Ph为水电输出功率；g为重力加速度，其值为9.81ms-2；ηh为发电机的效率；Q为水流量，m3s-1；ρ是水的密度，其值为1000kgm-3；h为水流下落的高度，m。

4 算例分析

本文选取新疆维吾尔自治区内可再生能源进行分析[20]。研究所使用数据包括水电站的典型输出数据及光伏电站、风电场采集的实时输出数据。对于丢失的数据，光伏数据为根据式（11）的计算值与前几天和后几天的同一小时观察结果之间的平均值，如果有两个数据顺序丢失，则应用每个小时的月平均值。风速缺失数据为式（12）的计算值与同一天的前一个和后一个观察值之间的平均值，如果有两个数据顺序丢失，则应用每个小时的月平均值。水电缺失数据被月平均值代替。

4.1 相关性研究

首先，对本文提出的优化Pearson 相关系数算法进行验证。取具有较强互补性的光伏与水电出力进行验证，针对光伏出力波动较大的情况，分别选取数据波动较小的晴天、数据波动较大的阴云天、几乎无出力的雨雪天三类数据与水电数据（见图1）进行相关性研究，对比传统Pearson 相关系数算法与改进Pearson 相关系数算法，得出表1。

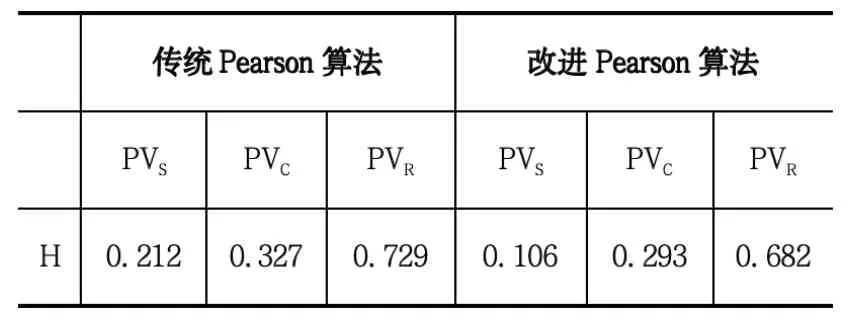
表1 改进Pearson 算法与传统算法对比

图1 水电与不同天气下光伏出力曲线

通过将H 分别与PVS、PVC、PVR三组数据进行相关系数计算，发现水电出力与光伏出力相关性较弱，具备一定互补性，这与光伏和水电出力的时间分布规律相符合。在光伏出力具有较大波动的多云、雨雪天气下，由于存在这些不正常的波动值，所以在与水电进行相关系数计算时，数据无法足够真实地展现它们的相关性。按照第3 章的方法对Pearson 相关系数算法进行优化，将两组数据进行对比，结合光伏与水电实际出力情况，证实了改进的相关性分析方法得到的相关性系数更加精确，更能反映数据间的相关性、互补性。

通过该方法对研究区域内各光伏电站（PV1、PV2）、风电场（W1、W2）、水电站（H1）进行相关性验证，相关性计算数据取2018 年6 月~2019 年6 月的Ppv、Pw、Ph数据。值得注意的是，在本研究中，假设理论上的发电厂将以任何太阳辐射、河流流量和风速值转换成能量。实际上，发电机的最大容量不仅受到额定功率的限制，还受到所用技术（如风力涡轮机的切入速度）或其他限制（包括水电站必须遵守的库容约束、流量约束等）。相关系数计算结果如表2 所示。

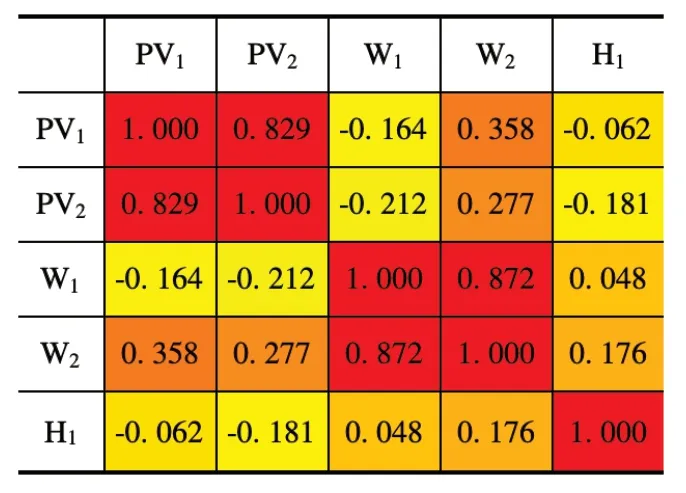
表2 基于日数据的光伏、风电、水电Pearson 相关系数

两个光伏电站之间具有强正相关性（0.829），两个风电之间也具有强正相关性（0.872），这种强相关性表面各电站处于相近或同一区域，同时根据新疆维吾尔自治区光伏、风电资源评估表明，光伏辐照与风速均随时间不断变化，因此两种能源间在空间与时间中均具有弱相关性（-0.164），即两种能源在发电过程中具备一定的互补性。

水电和光伏、风电之间存在弱相关性，这表明它们之间可能是具备较强互补性，水电可对光伏、风电进行及时的补偿。

4.2 多能互补优化配置研究

通过对100%光伏-风电-水电出力场景进行分析，计算发电量如何在其平均值附近变化，以证明可再生能源组合相对于单一能源发电的优点，进而获得最佳组合方案。

Pt指可再生能源的总组合功率，即用可再生能源组合代替单一能源的优势：

式中，Ph、Pw和Ppv分别是水力、风力和光伏发电能力，α和β是权重，α是水力发电对总功率的贡献，（1-α）β是光伏贡献，和（1-α）（1-β）是风电百分比。因此，当α=1 时，仅使用水电；当α=0和β=1，所有的电力都来自光伏；当α=0 和β=0 时，只有风电发电。假设每个电站对其电源最终功率的贡献相等。

根据式（14）计算总出力，其中，pt的标准差（sd）是要最小化的目标函数，取决于约束[0，1]。使用Matlab 代码从0 到1 变化，步骤为0.01。结果如图2 所示。

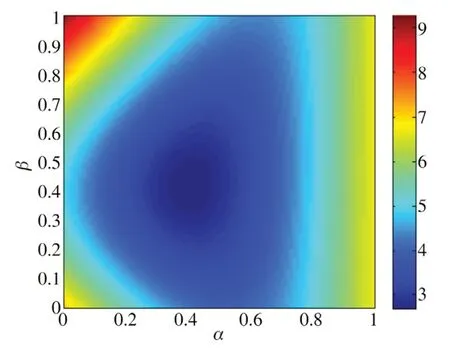
图2 按权重α 和β 得出的可再生能源总出力标准差

由图可以看出，当α=0.41，β=0.43 时，最小标准差为2.675，Ph=41%，Pw=34%，Ppv=25%。在纯光伏发电情景下（α=0 和β=1），最大标准差为9.298。当单一能源发电（α=0 和β=0――纯风电；α=0 和β=1――纯光伏；α=1――纯水电）时，出力标准差均大于多能互补发电时的标准差，从最坏情况到最佳情况的降幅为71.2%。结果表明，与单能模式相比，互补模式可以获得更稳定可靠的功率输出。

在该互补模式下，对研究区域可再生能源年出力情况进行分析，由于不同水电、光伏、风电机组装机容量与额定功率均不相同，各类能源的实际输出功率存在较大差别，为了便于对比分析功率互补性问题，对各个能源出力进行归一化处理。光伏、水电、风电及互补年出力曲线如图3 所示。可见，可再生能源会受季节与气候的影响导致出力在一年中具有较强的波动性，而通过互补方式对可再生能源加以利用，可以获得较为稳定的出力曲线。

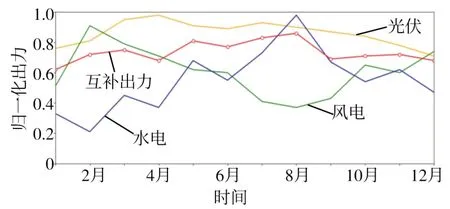
图3 互补运行方式下年出力曲线

如图4 所示，在日补模式下，当光伏发电量逐渐增加时，水电和风电的发电量可以减少，相当于将光伏发电量转化为水发电量存入水库。太阳能转换为水能后，通过水能的调节和存储功能，可以更有效地控制电力，从而能够在时间尺度上灵活分布。

图4 水电-光伏-风电日互补运行方式

利用这一组合比例来利用新疆维吾尔自治区的可再生能源，可以减少风能和光伏发电的弃电。对比互补能源模式和单一能源模式的弃电量，日弃电量如图5 所示。当光伏发电有较高的输出功率时，基本上在9：00~16：00 之间发生弃电，而互补模式的弃电量降低了28.7%。

图5 互补前后日弃电量

5 结束语

本文证实，将新疆维吾尔自治区内的水电、光伏和风能资源结合起来联合利用，可以有效增加对能源的利用率，同单一能源相比，互补运行方式可获得更稳定的功率（输出功率标准差降低71.2%），也可降低弃电量（日弃电量降低28.7%）。这种运行方式将可再生能源更高效地接入电网，减少弃风弃光，削弱对不可再生能源的依赖资源，同时降低发电成本，获取更大经济效益。

通过改进Pearson 相关系数算法对数据相关性进行计算，结合光伏与风电实际出力情况，证实了改进算法可以有效处理因天气波动产生的异常数据，获得更加精确，更能反映数据间的相关性、互补性的结果。

在工程实际中，最稳定的可再生能源组合高度依赖水力发电，而光伏发电与风力发电由于其间歇性、波动性，在互补运行的过程中仍会造成不利影响。因此，在现有能源组合的基础上，适当加入其他能源，如电池储能、空气储能、生物质能等，进一步改善光伏与风电的间歇性与波动性，获得更加高效、稳定的混合能源。

在下一步的工作中，进一步细化分析风电、光伏、水电小时互补性的评估，更好地了解在每一天的不同时期，各能源间应如何进行更好的互补利用，从而满足用电高峰期与低谷期的各类用电需求。