基于人工神经网络的碱矿渣混凝土强度预测

王雪芳,刘豪杰,马世龙,沈妍燃,吴文达*,许利惟,张晓平

(1.福州大学a先进制造学院,福建 泉州 362251;b.土木工程学院,福建 福州 350108;2.福建工程学院土木工程学院,福建 福州 350118;3.北方工业大学电气与控制工程学院,北京 100144)

目前,人们日益关注全球气候变化及其对社会产生的不利影响,这给最大温室气体生产来源之一的建筑业带来了巨大压力[1],同时也不符合我国的“双碳”发展目标,急需寻找一种高效水泥替代品。碱激发材料具有力学性能优异、耐高温、抗酸碱腐蚀性好、节能环保等优点,受到人们广泛关注[2-4]。与普通硅酸盐水泥相比,其制备过程不需要高温煅烧,碳排放量仅为普通硅酸盐水泥的26%～45%,是公认的绿色胶凝材料[5]。为了获得所需要的碱激发矿渣混凝土强度,通常要通过大量的试验去验证,这势必会带来各种资源上的消耗。因此,需要一个有效的强度预测模型来缩减大量不必要的试验,提高工作效率。

碱激发矿渣混凝土的内部组分对应关系复杂,不仅会受到水胶比、砂率等因素的影响,还受到碱激发剂的影响,这更加深了其复杂性。传统的预测模型虽然能一定程度地反映其复杂特性,但会受到变量复杂程度及人为因素的影响,具有一定的局限性,可重复性差[6],使得碱激发矿渣混凝土难以采用传统的以回归方法建立的预测模型进行精准预测。

人工神经网络正是模拟这种高度非线性关系问题的一种有效工具,人工神经网络模型在预测混凝土强度方面具有良好的精度与准确性[7-9],对于其他性能的预测也有较好的效果[10-11]。它可以很好地建立起混凝土与各影响因素之间的非线性映射关系[12],为碱激发矿渣混凝土强度的预测提供了有力的支持。

因此本文通过人工网络模型对碱矿渣混凝土的强度进行预测,并且针对传统BP网络模型对输入样本预处理方面的不足的缺点,引入了基于数理统计的主成分分析法(principal components analysis,PCA),对原始样本的影响因素进行降维处理,将多个输入变量转化为少数几个主成分,使这些主成分能够反映原始变量的大部分信息,从而提高运算效率,减少训练次数,以期能够达到更好的预测效果。

1 BP神经网络

1.1 BP人工神经网络模型简介

BP神经网络是基于BP算法和训练基础上形成的多层前馈网络,其应用范围较广泛,常常使用在多层网络计算中,最早提出该模型是在上个世纪80年代后期,并且在计算机领域发挥了重要作用和价值。其算法可以分为2个过程[13]:一是正向传播过程,从输入端开始,经过每一层结构完成计算,最终输出计算结果;二是反向传播过程,通过验证输出层的数据,若是数据与期望数据不符合,则会逐层重新计算,降低期望值与输出值之间的差距,以便根据此差值调节权值。权值和阈值不断调整的过程,也就是网络的学习训练过程,此过程会进行到所设定的误差值或者学习次数为止。

1.2 改进后BP算法与传统BP算法性能对比

BP算法是根据输出维度上的误差预测输出前导层的误差,通过误差对比计算能够预测出前一层的误差范围,经过不断循环计算,从而获得每一个维度上的误差。虽然这种误差估计本身的精度会随着误差本身的反向传递不断降低,但它的多层网络训练还是能够能逼近任意非线性函数。随着算法的演进与优化,常规BP算法的不足逐渐突出,主要体现在以下几个方面[13]:其一算法速度逐步下降,不论从理论研究上还是实践研究中,该算法训练路径都沿着误差曲面逐步逼进,随着神经元网络结构的复杂,使得误差曲面非常复杂且分布着许多局部极值点[14],在训练过程中一旦陷入了这些节点上,就会导致算法不能有序跟进,容易产生新误差问题。其二训练权值会逐步增大,使得节点输入变大,导致了其激活函数的导函数在该点的取值变小,使得训练路程增加,速度降低,网络逐渐停止收敛。针对以上缺陷,很多学者在不同方面对传统的BP算法进行改进,主要包括动量BP算法、学习率可变BP算法、弹性BP算法、拟牛顿算法、LM算法等。

利用BP神经网络强大的非线性逼进的特性对正弦函数y=sin(x)进行逼进,x值的选取是在[-3,3]以步幅为0.15取样,取x及其对应的y值作为网络的训练样本逼进正弦函数图像;取在[-3,3]以步幅为0.3取样的x作为检验样本,输入层神经元的个数为1,隐含层神经元个数为5,输出层神经元个数为1,即网络结构为1-5-1;隐含层的激活函数采用logsig函数,输出层采用purelin线性函数;训练算法分别采用传统BP算法、动量BP算法、学习率可变的BP算法、弹性BP算法、拟牛顿BP算法以及LM算法;以固定最大迭代次数2 000次,或最小均方误差0.000 1为训练结束的标准。

通过分析训练误差曲线对比得出:采用弹性BP算法、拟牛顿BP算法和LM算法的网络收敛性更好,利用这3种算法对正弦函数进行拟合,其具体的网络性能和预测结果比较如表1。

表1 3种改进算法的比较

综合分析以上3种算法,很明显,LM算法收敛速度最快,网络的训练误差最小,而且预测精度也最高。所以,本文后面对碱激发矿渣混凝土性能预测的BP网络模型的训练算法均采用LM算法。

2 强度预测模型的建立与分析

2.1 原始样本

参考了已有研究成果[15]中的相关实验数据,梳理后作为原始数据样本使用,并总结了5种常见的影响因素,分别为水胶比、碱当量、凝胶材料用量、碱种类、砂率,如表2所示。

表2 样本影响因素

2.2 选择网络激活函数

常见的网络激活函数模型主要有logsig、tansig、purelin模型。3类模型中logsig、tansig模型均表示微函数面模型,输入值取值范围在正负无穷之间,输出取值范围在0与±1之间;模型purelin属于线性函数模型,不论是输入层还是输出层,其取值是比较广泛的。对于激活函数模型选择,综合对比计算效果后进行确定。通过分析不同维度上激活函数对应误差,本文确定了组合类函数logsig-purelin,输入层到隐含层为logsig函数,隐含层到输出层为purelin函数,该组合函数能够有效稳定网络收敛效率。

2.3 根据统计理论构建BP网络模型

2.3.1 传统BP网络模型

输入数据和输出数据只做归一化处理,不做任何其他统计处理,本文把此种BP网络模型称之为传统BP网络模型(简称为T-BP网络模型)。T-BP网络模型训练步骤少,相关学习数据较少,整体上看网络收敛速度相对较合理,但是在实际训练过程中,发现网络存在不稳定问题,训练样本增加后,会存在冗余信息,训练时间会加长,从而使得网络收敛速度较慢,而且大量的冗余信息还会降低网络的预测精度。为了解决这些缺点,把数理统计理论中的主成分分析方法应用到神经网络中。

2.3.2 基于统计理论的BP网络模型

主成分分析法是常用的统计方法,就是利用降维思想[16],将多指标转化为少数几个可以最大反映原来多指标信息的综合指标。将PCA方法与BP网络相结合有以下优点:第一,输入层的神经元数量有相应的减少,网络结构变得简单;第二,能够对样本集中优化训练,在保障信息完整的基础上,降低了矢量维数,提高计算效率,使网络收敛速度加快,精度提高。本文把此种网络模型称之为基于统计理论的BP网络模型(简称为PCA-BP网络模型)。

2.4 PCA-BP与T-BP网络模型的性能对比

运用MATLAB7.0中神经网络工具箱(Neural Network Toolbox)编写相应的程序,建立T-BP网络预测模型和PCA-BP网络预测模型对碱矿渣混凝土的28 d抗压强度进行预测,以文献[15]中的数据作为训练样本,从本课题组长期以来进行的碱矿渣混凝土的试验研究数据中选取24组作为预测样本,从而比较这2种网络模型的性能。

2.4.1 样本数据的主成分分析

为了使样本不受量纲的影响,将样本数据进行标准化处理,将相关样本数据导入到公式(1)中:

(1)

式中:μi=E(xi),σii=Var(xi)。

利用MATLAB7.0中的相关函数对标准化处理后的数据进行主成分分析,经计算样本数据从原来的五维降为三维,同时为了避免输入或输出向量中数值大的分量绝对误差大,数值小的分量绝对误差小,对主成分分析后的输入、输出向量进行归一化处理,函数形式如式(2)、式(3)所示:

(2)

式中:xmin、xmax分别为样本数据组中网络输入向量的最小值、最大值。

(3)

式中:ymin、ymax分别为样本数据组中网络输出向量的最小值与最大值。

2.4.2 网络拓扑结构设计

1)输入层设计。T-BP网络模型的输入层神经元个数为5个;PCA-BP网络模型的输入层神经元主成分分析经主成分分析后个数为3个。

2)隐含层设计。隐含层节点数量的确认需要通过经验公式进行计算,计算式如下:

(4)

式中:n为隐含层上的节点数量;ni为输入层上的节点数量;n0为输出层上的节点数量,其中参数a一般为常数,取值范围在1～10之间。经过计算得出,隐含层上节点数量应该在4～13个之间,节点数量应该界定在4～20个之间。通过程序的搜索结果可知,T-BP网络模型和PCA-BP网络模型的最佳隐含层节点数均为12。

3)输出层设计。输出层参数即为碱矿渣混凝土28 d抗压强度,以此判断在该层上神经元个数为1个。

4)激活函数。其中输入层到隐含层采用了logsig函数,隐含层到输出层则选择了purelin函数。

5)训练算法。2种网络模型皆采用改进BP算法,即LM算法。

6)训练模式各种参数设计。训练模式中最大训练步数设计:net.trainP aram.epochs=2 000;性能误差参数设计:net.trainP aram.goal=0.001;确认失败的最大次数设计:net.trainP aram.max_fail=5;间隔显示步数设计:net.trainP aram.show=20;最大训练时间设计:net.trainP aram.time=inf。

2.4.3 预测结果

T-BP与PCA-BP网络模型抗压强度的实测值(f实际)、预测值(f预测)及相对误差(δ)结果如表3、表4所示。

表3 T-BP网络模型对碱激发矿渣混凝土28 d抗压强度的预测结果

表4 PCA-BP网络模型对碱激发矿渣混凝土28 d抗压强度的预测结果

T-BP网络模型和PCA-BP网络模型性能对比如表5所示。

表5 T-BP和PCA-BP网络模型性能比

T-BP网络模型与PCA-BP网络模型的实测值与预测值的拟合情况如图1、图2所示。可以看出,PCA-BP网络模型较T-BP网络模型表现出了突出的优越性。由于经过主成分分析,去除了原始试验数据中大量的冗余信息,使网络的计算效率提高,收敛速度加快,从而训练次数从195次减少到75次;另一方面,降低了原始数据中大量冗余信息所引起的网络误差振荡幅度,使网络的预测精度大幅度提高。T-BP网络模型的最大相对误差是PCA-BP网络模型的3.2倍,平均相对误差是PCA-BP网络模型的2.3倍,误差的振荡幅度比PCA-BP网络模型大得多。另一方面,T-BP网络模型的预测值与实测值的相关系数只有0.682 5,而PCA-BP网络模型为0.954 3,较T-BP网络模型大为改善,准确度更高,可以用于碱矿渣混凝土强度的预测。

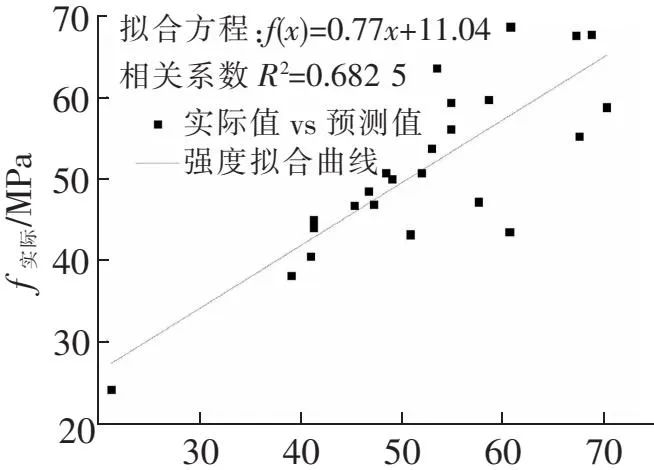
f预测/MPa

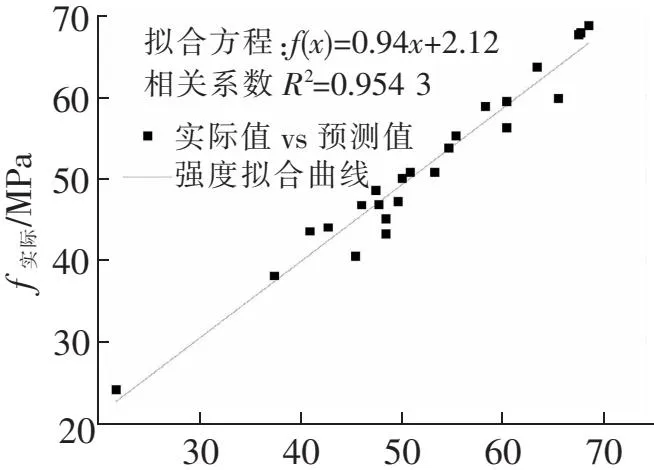
f预测/MPa

3 结论

1)本文使用T-BP网络模型和PCA-BP网络模型对碱矿渣混凝土的抗压强度进行预测,证明PCA-BP网络模型较T-BP网络模型训练时间短、收敛速度快、误差振幅小、预测精度高(R2=0.954 3),具有显著的优越性。

2)将上述的PCA-BP网络模型与全计算法相结合,以MATLAB为平台构建一种适用于碱矿渣混凝土强度预测的智能方法。此方法与计算机紧密结合,可以有效地预测碱矿渣混凝土的强度,能够在很大程度上减轻对人工和资源的消耗。