面向智能移动终端关键制造过程质量建模及优化分析*

任炎芳，刘志培，靳晓洋，张杨志

（1.广东虹勤通讯技术有限公司，广东东莞 523808；2.广东省智能机器人研究院，广东东莞 523808）

0 引言

随着智能移动终端产业集群规模不断扩大，产品质量是行业可持续发展关键，分析与掌握智能移动终端关键工艺机理与优化模型是提升产品质量首要任务。

国内外围绕智能移动终端产品质量建模与分析的研究主要通过实验设计、数学建模及数据挖掘等方式。文献[1]通过田口实验法对影响锡膏印刷质量的因素进行分析，归纳出最佳印锡组合。文献[2]通过控制变量实验、神经网络和响应曲面法优化锡膏印刷工艺。文献[3]建立了SMT 产线质量控制的决策支持模型的数据仓库，并依据SLIQ 算法提高了决策分析的准确性和可预测性。文献[4]利用样本累计误差值修正网络权值解决质量-工艺模型陷入局部最优等问题。文献[5]构造了焊点质量预测模型，获得焊点质量的主要影响因素。文献[6]基于有限元分析探究刮刀速度、角度对印锡工艺影响较大。文献[7-9]运用运筹学管理工具识别印锡关键参数，结合关联度与数值分析，确定了最佳参数组合。文献[10-11]基于BP 神经网络构建SPI 质量预测系统，以焊点形态实际值和理想值为模型输入，以工艺参数调整量为输出。上述国内外研究通过数据统计、神经网络等算法一定程度上探索了影响智能移动终端产品质量影响关键因素，但关联因素不够全面，分析机理依赖专家经验，缺少质量与工艺关联定量建模分析。

针对研究现状，本文通过质量与工艺关联优化模型，基于k-means、Apriori、粒子群等相关算法深入分析，对质量改善与工艺优化提供指导。

1 智能移动终端关键工艺机理

智能移动终端产线主要包括镭雕上料、印锡、SPI（锡膏检测）、贴片、回流焊接、AOI 以及后端的测试、组装和包装等工序，工艺路线长且参数复杂，其中SMT（表面贴装技术）产线段影响产品加工质量较为深远，其产线工艺机理如图1所示。

图1 智能移动终端产线流程

（1）镭雕及上料：PCB 主板上线，镭雕机与MES 系统集成，根据生产任务获取产品信息，自动生成二维码，通过镭雕机刻录到PCB主板上。

（2）印锡：通过刮刀将一定数量的锡膏通过专用钢网转移到印刷线路板上准确位置，包括印锡膏、锡膏填充和脱模3 个阶段，刮刀速度和压力、脱模速度和距离等工艺参数对产品质量影响程度高[12]，其工艺参数样例如表1所示（1 kgf=9.8 N）。

表1 印锡工艺参数样例

（3）SPI：通过激光、机器视觉等技术检验印锡工序品质，包括锡膏体面积、高度、偏移、漏印、凹陷等。上述指标控制阈值的设定影响着整体质量检测与判别的效果。在实际生产中各项控制线的设定是根据人工经验，且在引入新产品时控制线阈值需再次调整，难以适应当前多品种柔性化定制化生产需求。检测数据样例如表2所示。

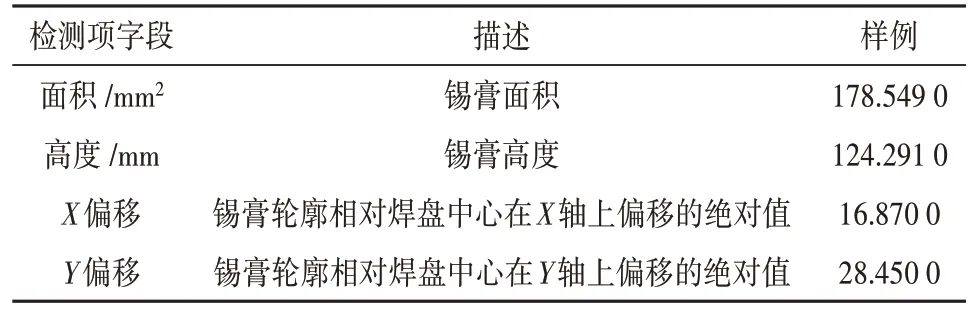
表2 SPI检测数据样例

（4）贴片：即表面贴装，通过定位、X-Y运动、吸料等操作将电子元器件放置在PCB主板上。

（5）回流焊接：在回流焊机内通入大量惰性循环气体，通过加热融化锡膏，使得表面贴装元器件和PCB 主板可靠的结合在一起并冷却凝固。

（6）AOI 检测：通过机器视觉技术获取PCB 主板图像，上传系统与标准参数进行对比，检测主板缺陷并将结果展示出来。

2 关键工艺质量缺陷识别与建模分析

2.1 识别过程建模

印锡是SMT 产线制程首道工序，数据统计表明，印锡环节产生的缺陷占整体缺陷总数的60%～70%[13]。印锡质量检测主要通过SPI 环节完成，利用3D 视觉技术检测焊盘上锡膏的体积、面积、高度以及拉尖等项目，并通过对这几项质量指标的控制来保证印刷质量，但SPI检测存在误报率较高、缺陷类别需要经过人工视检进行确定等问题。常用的SPC 分析以及在线监控方式难以实现有效改进，本文基于数据挖掘和K-means算法，为SPI检测提供新的缺陷类别智能判断模式，提高产品质量，如图2所示。

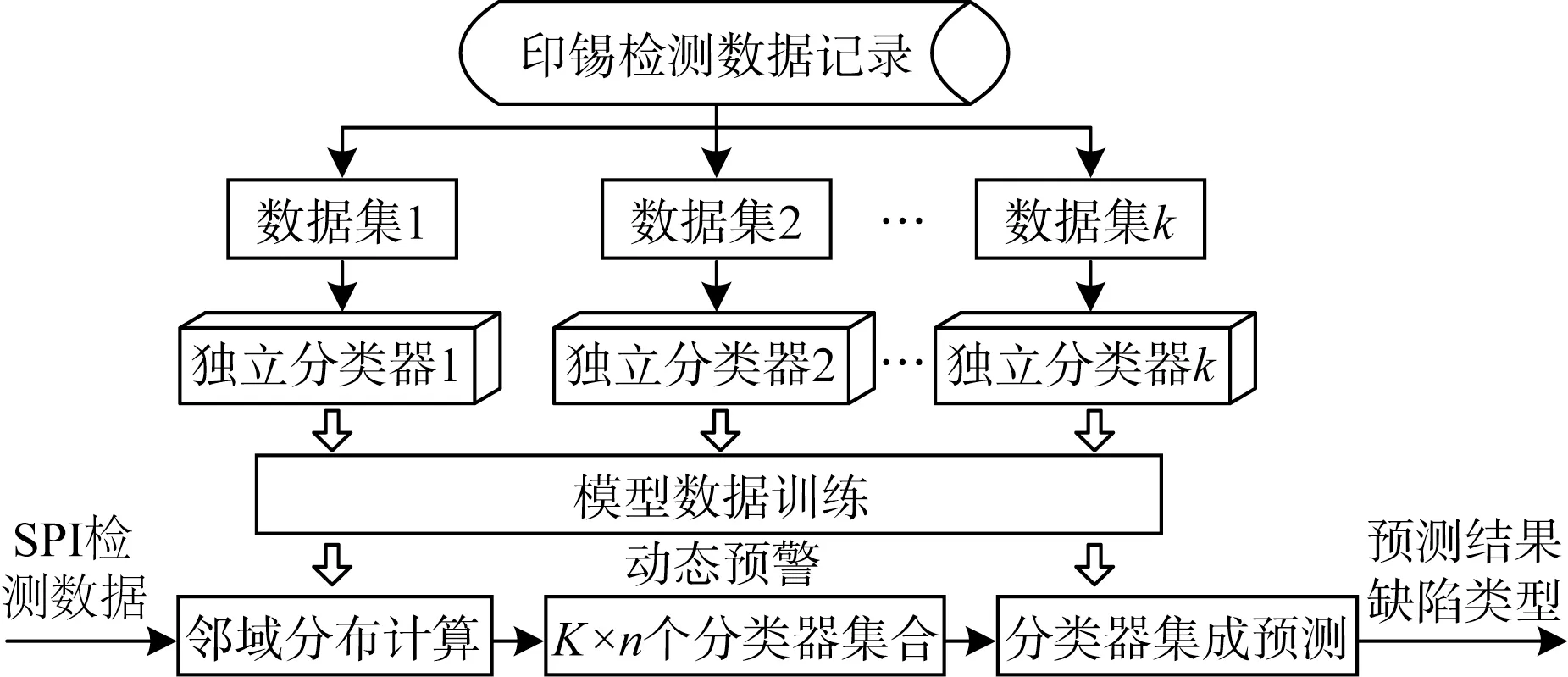
图2 缺陷类别判定模型流程

（1）印锡检测数据聚类分析与处理

聚类分析将大量数据进行集中分类，使得每个类别数据之间最大程度相似。本文基于k-means 算法实现印锡检测数据样本聚类分析，在欧氏空间内，对于给定的n个d维数据点的数据集X={x1,x2,…,xn} 以及要生成的聚类数目K，k-means 聚类给出该数据对象的K个划分，即C={ck,k=1,2,…,K} 。该算法选取欧式距离为相似度判断标准，计算每个类别中各个数据点到聚类中心点的距离累计最小，从而得到聚类结果。

（2）独立分类器训练：在检测数据聚类基础上基于数据挖掘技术找出同一类别组内存在的缺陷模式。首先在原始训练数据集上找出待测数据x的领域φx=n，考察φx=n在K个聚类组上的分布数量，进而在相应聚类组上随机选择对应分布数量的分类器，得到动态选择的分类器集合并进行集成训练，规则如下：

即当n个独立分类器的输出全部为0，则判断结果为无缺陷，当存在1个输出为1时，如果与该输出同类别的其他独立分类器有超过3个输出为0，则判定该检测数据无缺陷，而同组其他分类器数量不足，则发出警报请求人工确认。

2.2 关键工艺质量缺陷识别模型优化分析

由于k-means 算法初始聚类中心是随机生成的，当选择点落在孤立点、噪声点或边界上将影响聚类结果的稳定性与准确性，为此本文根据检测数据样本空间分布紧密度信息，提出利用最小方差（紧密度最高）优化初始聚类中心的k-means 算法，方差是数据集内各数据与其平均数之差的平方和的期望，衡量一个样本波动大小的量，是离散趋势最重要和最常用的指标。改进的kmeans 算法通过计算数据集所有样本方差，以及所有样本间的距离均值R，启发式地选择位于样本分布密集区域，且相距较远的样本为k-means 初始聚类中心。启发式选择过程为：首先选择方差最小的样本作为第1 个类簇初始中心，以R为半径画圆，在圆之外的样本中，寻找方差最小的样本作为第2 个类簇初始中心，以R为半径画圆；重复在剩余样本中选择下一个类簇的初始聚类中心，直到第K个类簇初始中心被选择到[14]，改进的kmeans方式核心算法如下：

所有样本的集合为W，待聚类的数据集为：X={xi｜xi∈R,i=1,2,…,n}，K个初始聚类中心分别为C1，C2，…，Ck，用W1，W2，…，Wk表示K个类簇所包含的样本集合。

样本点距离公式为：

任意样本点到所有样本点之间的平均距离公式为：

样本xi的方差值公式为：

所有样本点的平均距离公式为：

聚类误差平方和公式为：

根据SMT 产线上印锡SPI 检测历史数据中随机抽取100组数据，如表3所示。

表3 SMT产线印锡检测样本数据

根据改进的k-means 算法的印锡质量缺陷识别模型，通过聚类分析判定样本内异常点，其异常判定求解流程如图3所示。

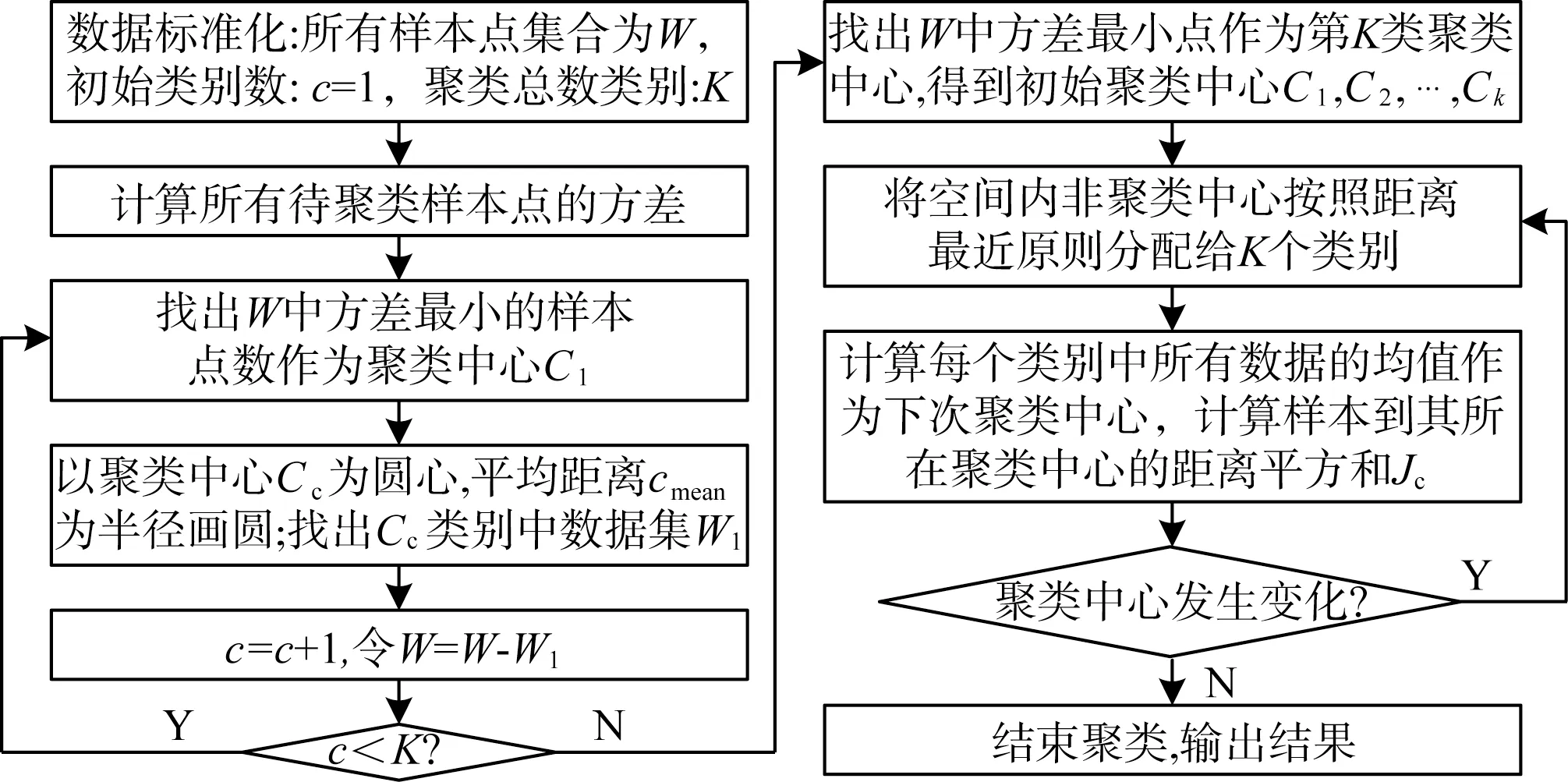
图3 基于改进k-means的聚类分析流程

（1）确定初始聚类中心：计算数据集内每一个样本的方差，寻找最小方差作为第一个类簇初始聚类中心；

（2）令c=1，w=w-w1，若c＜K，则令c=c+1，在剩余样本中继续寻找方差最小样本，得到初始聚类中心C1，C2，…，Cn；

（3）建立目标函数，计算数据集内每个样本到初始聚类中心距离和聚类误差平方和；

（4）将特征点相对距离与阈值进行对比，超过阈值，则标记为异常点；

（5）聚类中心不发生变化时计算终止。

将表3 内基础数据代入至模型内进行分析，识别异常样本点，如图4 所示，其中蓝色代表正常值，红色代表检测出的异常点。

图4 基于改进k-means算法的离散点距离异常检测

3 产品质量与关键工艺关联分析

在关键工艺质量缺陷识别基础上，通过关联产品与关键工艺关系，挖掘产生质量异常条件下核心影响要素。

3.1 关联分析规则模型

Apriori 是一种关联规则挖掘算法，主要研究对象是事务数据库，目的是发现大量数据中项集之间有意义关联关系或规则。其数学定义如下：设I={I1,I2,…,Im} 是m个项的集合，事务T是I的子集，事务集D是不同事务的集合，关联规则是形如X⇒Y的蕴含式，其中X和Y均是I的子集，且两者之间无交集。关联规则有2个基本概念：支持度和可信度[15]。

（1）支持度描述了2个项X和Y同时在事务集D中出现的概率，记作support(X→Y)，计算公式为：

其中，最小支持度为关联规则重要性最低的阈值，由专家或用户定义，若support(X)≥min sup，则称X为频繁项集。

（2）置信度描述了在X 出现的情况下，同时出现Y的概率，即条件概率P(Y｜X)，记为confidence(X→Y)：

其中，最小置信度为关联规则可靠性最低的阈值，也是由专家或用户定义。在实际产品质量与工艺参数关联规则处理中，以最小支持度和最小可信度为目标，建立基于Apriori 的影响印锡质量因素关联分析模型，寻找频繁集，将每个候选项集与数据库中的所有交易依次进行匹配，若该候选项集是交易的子集，将其支持度计数加1，从所有候选项集中找出满足support(X) ＜min sup的项集。基于频繁项结果搜索的基础上挖掘出有价值的关联规则，其建模流程如图5所示。

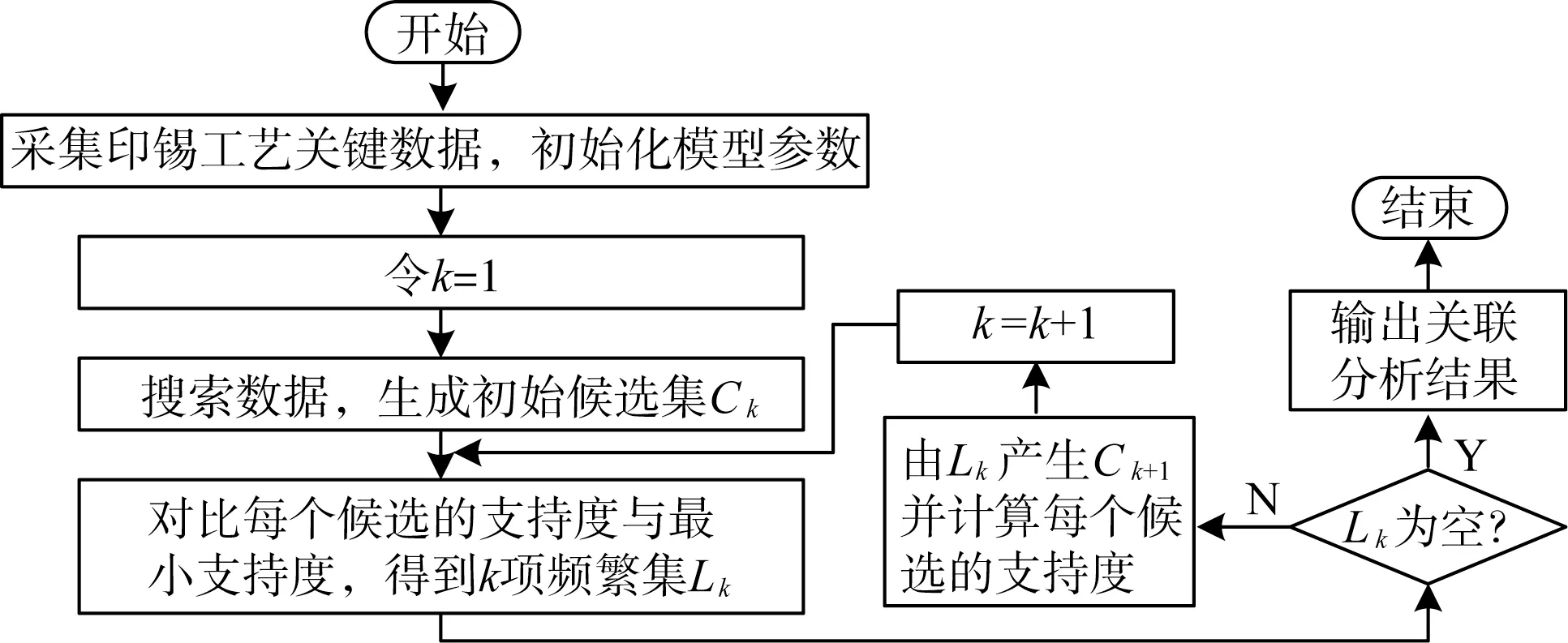
图5 基于Apriori的印锡质量关联分析建模流程

3.2 产品质量与关键工艺参数关联分析

为验证产品质量与工艺参数关联关系，获取18 092条SPI数据进行分析。

基于Apriori 建立缺陷质量关联模型，通过相关系数及工艺机理编译印锡质量影响因素特征层次及特征值，以离散编码方式匹配影响因素特征值区间[16]，例如刮刀速度离散编码对应特征值区间x1～x10，例如第一类要素刮刀速度15 mm/s 对应层级为7，记为。通过专家定义设置最小支持度设为0.5，最小置信度为0.6，对表4检测数据进行关联分析，如表5所示。

表4 印锡关键参数记录

表5 印锡质量与工艺关联分析

以第1 个样本为例，支持度和置信度较低，解码结果为锡膏高度低、体积小，导致该现象原因是锡膏颗粒不够饱满，刮刀平均速度和压力较大，在实际生产过程中，容易出现锡膏分布不均匀，影响元器件电路性能。

4 基于粒子群算法的关键工艺参数优化

在印锡质量与关键工艺关联模型基础上，通过构建质量-工艺优化模型反向优化印锡工艺参数，依据质量缺陷数据聚类分析，以印锡质量指标稳定性（例如高度H波动最下）构建目标函数。根据印锡质量缺陷建模可知，质量指标均值和方差可反映质量波动情况，依此构建锡膏高度指标与工艺参数优化模型。

式中：λ为权重系数，λ∈[0,1]；h1(X)为锡膏实际高度值；为高度均值；(X)为锡膏高度方差；X=[x1,x2,…,xn]T为印锡工艺参数特征组合，包括刮刀速度和压力、脱模距离和速度等。

采用粒子群优化算法对上述目标函数进行求解，步骤为：（1）根据生产现场工艺要求，确定工艺参数区间，例如刮刀速度x1∈[20,40 ]；（2）目标函数权重系数λ初始值为0，设置初始种群和维度，粒子群模型迭代5 000次；（3）将工艺参数（粒子群）代入模型，即计算每个粒子个体对应的锡膏高度差与方差；（4）依据高度差与方差值计算minH(x)，确定最优个体及群体，更新粒子速度和位置；（5）判断迭代次数是否达到5 000次，若达到，记录并保存群体最优适应度，更新λ=λ+1，否则返回（2）；（6）判断λ是否等于1，若λ=1则优化结束，否则返回（3）。

通过上述步骤，权重系数λ取值每更新一次，产生对应的目标函数值，将表3 原始数据代入模型，结果如表6所示。

表6 不同目标函数对应最优解

通过粒子群算法得到最优解，当λ=0.1 时，获得最佳工艺参数组合，即{刮刀速度，刮刀压力，脱模速度，脱模距离，清洗速度}=[x1,x2,x3,x4,x5]T=[25,8,0.7,2,25]T。

5 结束语

本文在智能移动终端产线关键工艺机理研究基础上，构建PCB 主板锡膏高度质量指标与印锡工艺刮刀速度和压力、脱模速度和距离等关键参数关联模型。本文根据检测数据样本空间分布紧密度信息，提出利用最小方差优化初始聚类中心的k-means算法完成海量SPI检测数据的聚类分析与异常数据识别，为产品质量与关键工艺关联提供基础。通过Apriori 关联模型定性分析产生异常质量情况的重要影响因素，以锡膏高度差与方差最小化为目标函数，构建质量-工艺优化模型反向优化刮刀速度和压力、脱模速度和距离等印锡关键工艺参数，基于粒子群算法优化求解模型，在最优质量指标下输出最佳工艺参数动态组合。