Lasso-Cox回归构建直肠癌预后模型并验证

李德关,汪圣毅,刘 虎,张 震,李永翔

直肠癌预后与患者的总生存期[1]和无进展生存期[2]有关。对关键因素进行干预可改善预后,提高疗效[3]。然而,用统计模型筛选预后影响因素的过程中,当纳入的变量过多时,数据的维度增加,样本量相对不足,不利于影响因素的有效筛选,此外,当变量之间高度相关时,可导致维度灾难的发生,会削弱模型的准确性、稳定性[4]。最小绝对收缩和选择运算(least absolute shrinkage and selection operator,Lasso)可有效筛选变量,已被广泛应用于线性模型的数据分析[5]。目前,基于Lasso方法的Cox回归被广泛运用于肿瘤预后标签的筛选和风险模型的构建[6],较传统方法有明显优势。但在直肠癌的预后影响因素研究中多用于基因标签的筛选,而临床和病理变量指标筛选后构建预后模型的研究较少。现有研究仅局限于根据特定的临床病理特征进行分层分析的直肠癌样本,仍缺乏临床自然样本的模型研究。本文收集临床和病理指标数据,用Lasso-Cox回归方法分析直肠癌的预后影响因素,构建预后影响因素的预测模型,绘制列线图,并进行综合评价,旨在对直肠癌的预后研究提供基础。

1 材料与方法

1.1 研究对象收集安徽医科大学第一附属医院2015年1月至2021年5月的599例直肠癌数据,纳入标准:①诊断具有病理依据;②临床资料完整。排除标准:①数据存在缺失值、异常值;②研究变量中的分类及其亚类不明确或者没有被评估;③分类变量的亚类评估不正确或者记录错误。收集的变量包括:①人口学特征:性别、年龄、身体质量指数;②临床特征:糖尿病、术前营养评分(nutrition risk screening, NRS2002)、ASA分级、血红蛋白、白蛋白、癌胚抗原、糖类抗原199(carbohydrate antigen199, CA199)、肿瘤至肛缘距离、新辅助化疗、手术时间、出血量、是否开放手术、造口、术中输血、引流量、术后化疗、放疗、复发、转移、生存时间;③病理特征:肿瘤直径、组织学分级、远切缘距离、血管侵犯、神经侵犯、癌结节、术后(T、N、M、TNM)分期。

1.2 变量定义及分组癌结节是指术后病理检查的肿瘤结节,衡量癌细胞浸润和转移的情况,有癌结节=1,无癌结节=0;性别:女=0,男=1;糖尿病:无=0,有=1;新辅助治疗:无=1,化疗=2,放疗=3;开放手术:否=0,是=1;有无造口:无=0,有=1;术中输血:无=0,有=1;组织学分型:高分化腺癌=1,中分化腺癌=2,低分化腺癌=3,粘液腺癌、印戒细胞癌、其他及未评估=4;血管侵犯、神经侵犯、癌结节、术后化疗、放疗、复发、转移均编码为:无=0,有=1;根据美国癌症联合委员会第8版进行术后T、N、M、TNM分期;Tis+T1=1,T2=2,T3=3,T4a+T4b=4,N0=1,N1=2,N2=3,M0=1,M1=2,TNM Ⅰ、Ⅱ、Ⅲ、Ⅳ期分别为1、2、3、4。见表1的第二列。

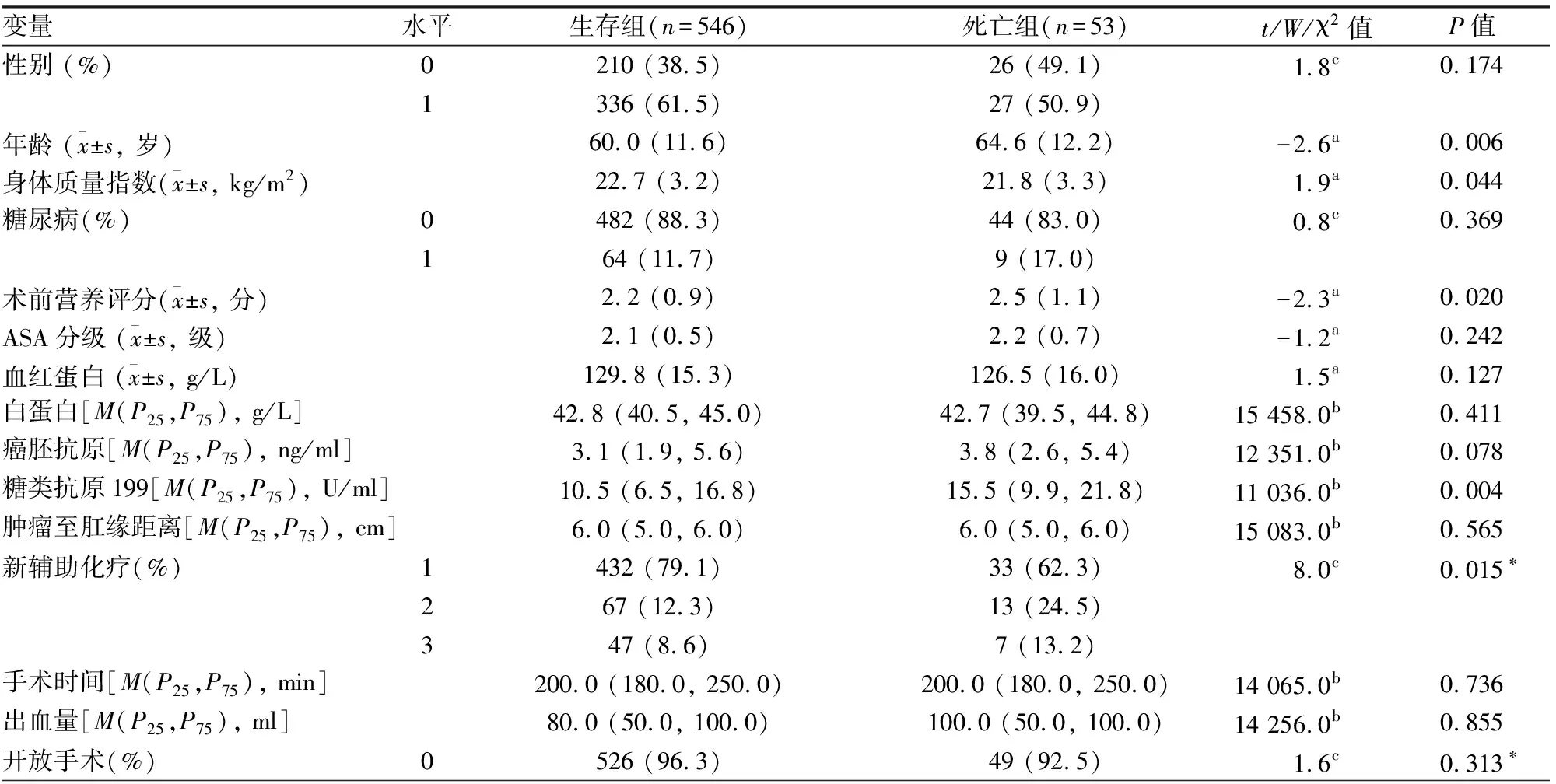
表1 随访的生存组和死亡组的特征比较

1.3 Lasso回归分析采用Lasso回归进行L1范数约束,控制lambda(λ)参数调整模型的复杂度,以便进行变量的筛选。重新将因子变量的不同分类编码为整数,哑变量化展平,转为矩阵形式,与连续变量合并为数据框,转为矩阵,glmnet包进行Lasso回归筛选变量。

1.4 Cox回归分析利用Lasso回归筛选系数不为0的变量作为自变量,用rms包的cph函数进行Cox回归分析,建立患者术后生存影响因素的Cox回归模型。

1.5 列线图的建立与评估定义time.inc为1年、3年,nomogram函数绘制Cox回归的列线图;利用已建立的Cox回归模型:h(t,X)=h0(t)exp(β1X1+β2X2+…+βnXn),计算模型中的线性预测值(linear prediction,lp):lp=(β1X1+β2X2+…+βnXn),用lp计算1年、3年生存的假阳性(false positive, FP)、真阳性(true positive, TP)值;绘制受试者工作特征曲线(receiver operating characteristic curve, ROC),梯形法则计算ROC曲线下的面积(area under the ROC curve,AUC);在polspline包中使用hare函数对模型预测1年和3年生存概率的一致性进行检验,绘制校准曲线,自助抽样次数B设置为200次;使用决策曲线分析(decision curve analysis, DCA)评估模型的净获益情况。

2 结果

2.1 直肠癌根治术患者生存组和死亡组的一般特征比较599例的患者年龄22～90岁,中位年龄61岁;其中,男性363例,女性236例;平均随访时间为48.5月; 546例患者生存, 53例患者死亡;生存组和死亡组的临床特征比较,发现:死亡组患者的年龄较大、BMI较低、术前营养评分和CA199较高,两组间差异具有统计学意义(均P<0.05);生存组与死亡组之间的术前新辅助治疗、术中输血、血管侵犯、神经侵犯、癌结节、术后的T、N、TNM分期、放疗、术后是否复发转移差异有统计学意义(均P<0.05),死亡组的中位生存时间较短(P<0.001)。见表1。

2.2 Lasso回归结果Glmnet函数的family参数设定为Cox,经过压缩算法,多数变量的回归系数被压缩为0。见图1。用10折交叉验证法,绘制均方误差(mean square error,MSE),随着lambda(λ)参数自然对数变化的情况,当λ最小值为0.016,即其对数值为-4.105时,MSE为最低(左侧虚线),右侧虚线为1个标准误差内的λ值。见图2。系数不为0的8个变量分别为:是否术中输血、术后淋巴结分期、术后化疗、复发、转移、神经侵犯、年龄、BMI。

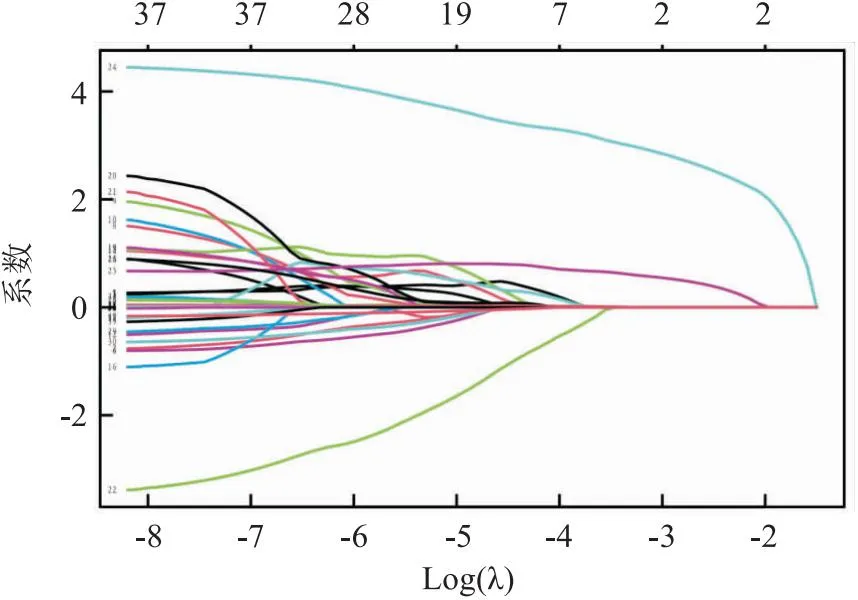
图1 变量系数随lasso回归参数的变化

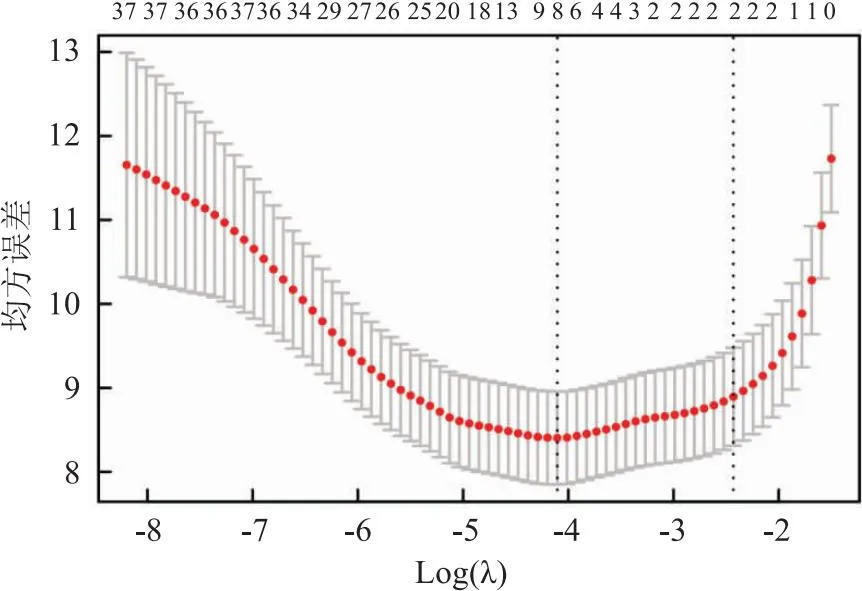
图2 均方误差随Lambda对数值的变化

2.3 Cox回归结果Cox回归模型的似然比检验值为214.6,P<0.01。年龄、BMI、术中输血、术后化疗、复发、转移是影响直肠癌预后情况的独立因素。见表2。

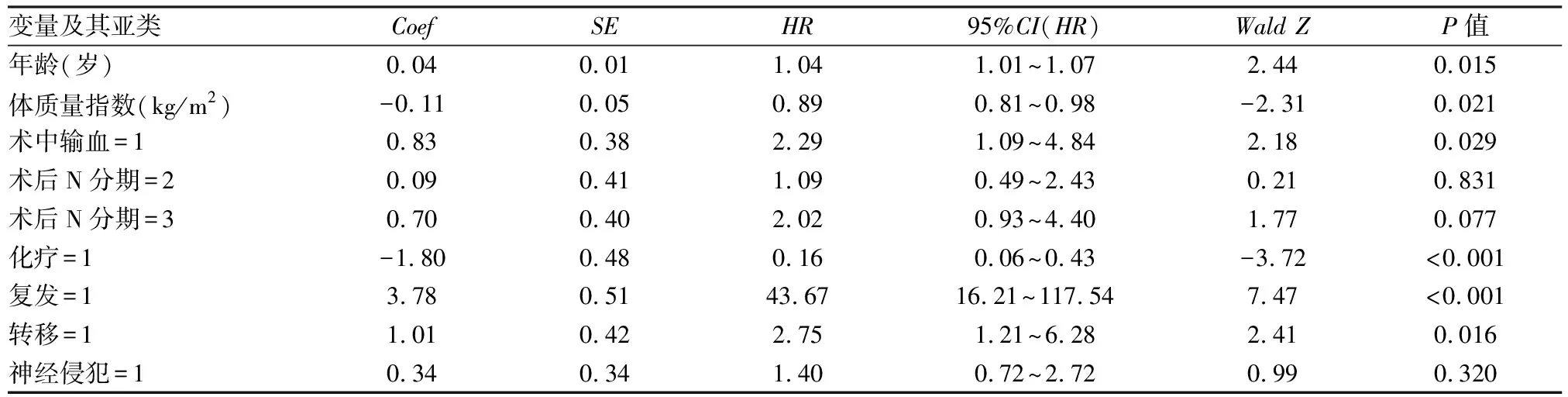
表2 cox回归结果

2.4 列线图对Cox回归模型中的自变量进行得分计和后,用列线图展示了对直肠癌患者术后1年、3年生存率的影响。结果显示,与无神经侵犯的患者比较,有神经侵犯的患者评分增加6分。有转移的患者评分较无转移患者增加17分。有复发患者的评分较无复发患者增加65分。化疗患者较未化疗患者评分减少32分。术后N分期为3的患者较分期为1的患者增加12分。体质量指数每增加4 kg/m2,模型评分减少8分。年龄每增加10岁,评分增加6分。见图3。

图3 预测直肠癌手术后1年、3年生存率的列线图

2.5 模型评价通过重采样方法估计预测值与观测值的一致性概率,得出模型的C指数为0.950,se=0.011,模型区分度良好。模型判断是否死亡的AUC为0.95(95%CI: 0.91～0.99),P<0.01。见图4。预测直肠癌手术后1年和3年生存率的校准曲线显示,模型预测概率和实际概率较为接近,一致性较好。见图5、图6。DCA绘图显示,DCA曲线远离了平行于X轴的决策线斜率为负数的虚线,表明净获益率显著高于两种设定条件。见图7。

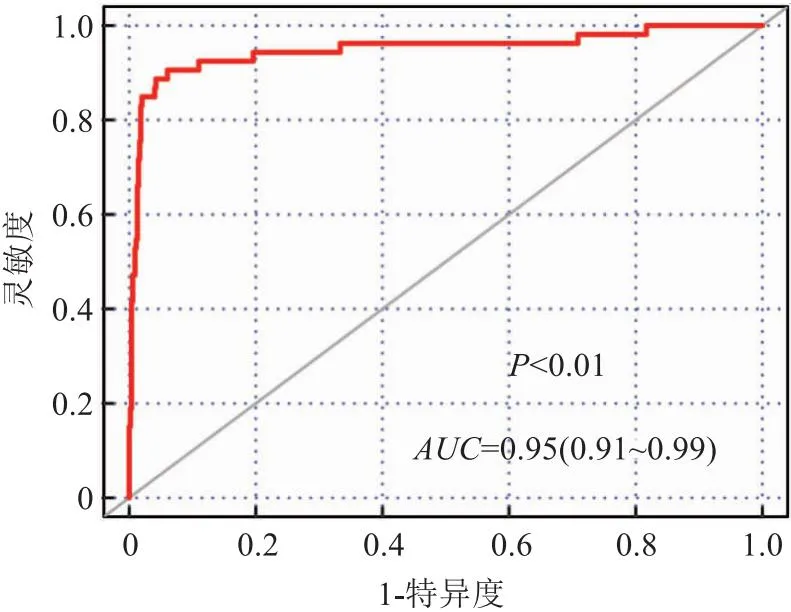
图4 模型预测术后死亡的ROC曲线

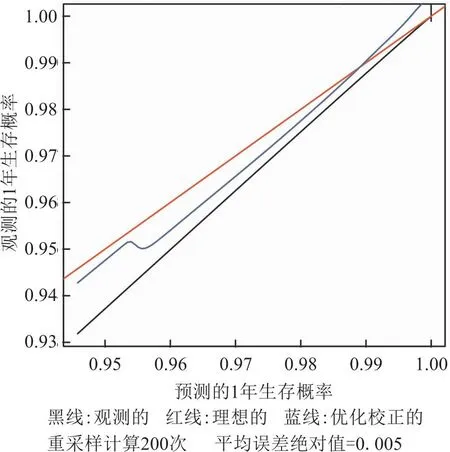
图5 模型预测术后1年生存率的校准曲线

图6 模型预测术后3年生存率的校准曲线

图7 临床决策曲线

3 讨论

直肠癌手术后的生存时间和生存概率受多种因素的影响,既往研究[7]报告与多种表观遗传学基因标签有关,与临床、病理因素的关系尚不明确,并且既往研究结果大多基于传统的Cox回归方法,无法避免维度灾难,结果发生偏差的可能性较大。采用Lasso-Cox回归建立高维度数据的预后影响因素模型较传统单一的Cox回归方法更加准确可靠。

利用临床、病理数据构建的Lasso-Cox回归的直肠癌预后模型较少,本研究利用临床、病理资料,基于Lasso-Cox回归方法建立预后模型,绘制列线图。模型判断直肠癌手术后是否发生死亡的AUC值为0.95,预测准确性高,校准曲线的一致性较好,DCA曲线显示临床获益明显。

本研究发现多个因素与术后死亡存在关联,Lasso回归筛选出8个变量:术中输血、术后淋巴结分期、术后化疗、复发、转移、神经侵犯、年龄、体质指数;建立Cox模型后发现:术中输血、年龄、复发、转移为危险因素,术后化疗、BMI为保护因素。对于医院的直肠癌人群,用Lasso-Cox方法进行预后分析的研究较少。对T3N0M0直肠癌患者的研究[8]发现,年龄、单核细胞百分比、淋巴结清扫数目、神经侵犯是直肠癌预后的独立影响因素,与本研究发现的预后因素存在差异,可能与纳入人群不同有关。研究发现[9]化疗可以通过改变细胞的多种内部机制改变肿瘤相关特征。对新辅助治疗后行全直肠系膜切除术的患者的Cox回归研究[10]发现,与偏瘦人群比较,正常体重、超重患者的无病生存期的HR小于1。此外,Ⅱ、Ⅲ、Ⅳ期的直肠癌患者中,BMI高的亚组预后较好[11],与本研究发现相一致。本研究发现术中输血、复发、转移是影响直肠癌根治术后生存概率的独立危险因素,与既往研究结果一致[12-14]。本研究发现,年龄每增加1岁,死亡风险增加3.57%,然而有研究[15]发现年龄对预后的作用也存在非线性关系。因此,用混合效应模型、样条回归等方法是进一步研究的方向。

采用多种方法进行模型综合评价,可以显著提高模型的可靠性。本研究联合使用ROC曲线、校准曲线、DCA方法,对构建的模型进行评价。区分度优于以往的报告[8]、一致性相当、DCA曲线显示模型获益较好。本研究利用电子病历中术前、术中、术后的相关指标,建立Lasso-Cox回归模型和列线图来预测直肠癌的预后,指标采集方便,可行性高,为直肠癌患者术后的生存预测研究提供了新的思路。然而该研究也存在一定局限性,样本量有限,仅用再抽样方法进行校准曲线分析,未来需要进一步增加样本量,建立训练集、验证集、测试集,优化模型。