巧用“电场线法”破解静电场问题

毛广文

(河南省开封高级中学)

电场线定性描述电场分布,应用电场线解决问题可以达到简捷、形象、生动的效果.电场线特性可以用“强弱看疏密,方向沿切线,电势顺线低,不交、不切、不闭合”进行表述.将电场线巧妙地与电荷电性、电荷运动、电场力做功与电势能变化、复杂电场分析等知识相结合,利用“电荷在一根电场线上运动的过程”来分析电场中的问题,能启迪思路,化繁为简.下面通过几个实例,利用“电场线法”巧解电学题,以飨读者.

1 常规问题中的“电场线法”

学生常会遇到电荷在电场中运动的相关问题.借助辅助信息,对电荷受力情况和运动情况进行分析,进而实现对相关电场特点的判断,是“电场线法”的常规应用,此时要注意利用电场线“强弱看疏密,方向沿切线,电势顺线低”的特点.

例1如图1所示的直线是真空中某电场的一条电场线,A、B是这条直线上的两点,一带正电的粒子以速度vA向右经过A点向B点运动,经过一段时间后,粒子以速度vB经过B点,且vB与vA方向相反,不计粒子重力,下面说法正确的是( ).

图1

A.此电场一定是负电荷形成的电场

B.A点的电势一定低于B点的电势

C.粒子在A点的速度一定小于在B点的速度

D.粒子在A点的电势能一定小于在B点的电势能

由于只有一条电场线,故无法确定电场是由何种电荷形成的,选项A 错误.由速度反向可知,粒子受到的电场力方向向左,所以从A点到B点,电场力做负功,电势能增加,选项D 正确.由运动的对称性可知选项C 错误.由于粒子带正电,说明电场强度方向向左,根据“电势顺线低”判定B点的电势高,选项B正确.答案为B、D.

例2一带电粒子仅在电场力作用下从A点开始以初速度－v0做直线运动,其v-t图像如图2所示.粒子在t0时刻运动到B点,3t0时刻运动到C点,以下判断正确的是( ).

图2

A.A、B、C三点的电势关系为φB＞φA＞φC

B.A、B、C三点的电场强度大小关系为EC＞EB＞EA

C.粒子从A点经B点运动到C点,电势能先增大后减小

D.粒子从A点经B点运动到C点,电场力先做正功后做负功

根据运动图像分析可知,粒子沿直线先向负方向运动到B点,速度减为零后再向正方向运动到达C点.由于粒子电性未知,无法确定电场强度的方向,因此无法比较电势的高低,故选项A 错误.由v-t图像的斜率表示加速度可知,粒子的加速度先增大后减小,且在B点时加速度最大,根据牛顿第二定律得qE＝ma,可知B点的电场强度最大,故选项B错误.由图像可知,粒子从A点经B点运动到C点过程中,速度先减小后增大,所以动能先减小后增大,根据能量守恒定律可知,电势能应该先增大后减小,故选项C正确.根据动能定理可知电场力先做负功,后做正功,故选项D 错误.答案为C.

2 复杂电场中的“电场线法”

电场作为看不见、摸不着的特殊物质,学生学习起来比较困难,对于复杂电场相关问题的分析更是感觉无从下手.借助“电场线法”对电荷在复杂电场中的运动情况进行分析将会使解答思路变得简捷明快.

具体做法如下:画出一根电场线由M点指向N点的,根据“电势顺线低”的特性,可以判断出M点电势高于N点电势,依据题意将正(负)电荷置于其上,根据题目中对电荷移动情况的表述,将电荷在高低电势之间移动并对电荷移动过程中的受力情况进行分析,从而确定电荷在运动过程中的做功情况和能量转化情况.

例3如图3所示,在真空中的A、B两点分别放着等量异种电荷＋q、－q,在通过A、B两点的竖直平面内相对于AB对称取一个矩形路径abcd,现将一个电子沿abcd移动一周,则下列说法正确的是( ).

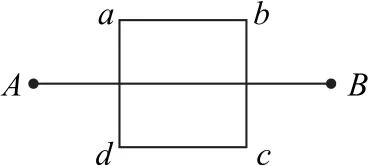
图3

A.由a到b,电势降低,电子的电势能减小

B.由c到d,电势升高,电子的电势能增大

C.由b到c,电场力对电子先做正功,后做负功,总功为零

D.由d到a,电子的电势能先减小后增大,电势能总变化量为零

如图4所示,根据等量异种电荷电场电势分布关系可知φ1 ＞φ2 ＞φ3＞φ4＞φ5,电子沿abcd移动一周的路径中的电势变化情况复杂,而借助“电场线法”进行分析,则简捷明快.

图4

画出一根由M点指向N点的电场线,根据“电势顺线低”的特性,可以判断出M点电势高于N点电势,电子在M、N之间受力方向指向M点.电子在abcd上的运动情况可以转化为在MN间移动,则可以借此对电子运动过程中的做功及电势能变化情况进行分析.

当电子由a到b运动时,电势降低,等效于电子从M到N,由于电子所受电场力指向M点,故电场力做负功,电势能增加,选项A 错误.当电子由c到d运动时,电势升高,等效于电子从N到M.由于电子所受电场力指向M点,故电场力做正功,电势能减小,选项B错误.当电子由b到c运动时,由图可知,其路径上电势先降低再升高,等效于电子先从M点移到N点,再从N点移到M点.由于电子所受电场力指向M点,故电场力先做负功再做正功,总功为零.电势能先增大再减小,选项C错误.当电子由d到a运动时,由图可知,其路径上电势先升高再降低,等效于电子先从N点移到M点,再从M点移到N点,由于电子所受电场力指向M点,故电场力先做正功后做负功,总功为零.电势能先减小再增大,电势能总变化量为零,选项D 正确.答案为D.

例4位于A、B处 的两个带有不等量负电的点电荷在平面内电势分布如图5所示,图中实线表示等势线,则( ).

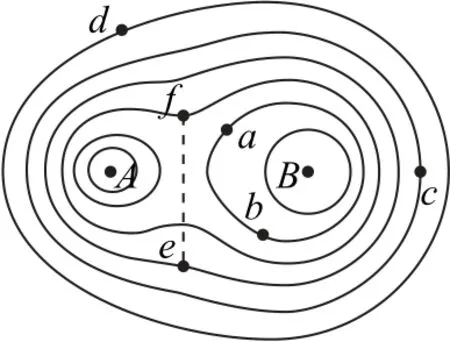
图5

A.a点和b点的电场强度相同

B.正电荷从c点移到d点,电场力做正功

C.负电荷从a点移到c点,电场力做正功

D.正电荷从e点沿图中虚线移到f点,电势能先减小后增大

对于此电场的电势分布情况进行分析可知φd＞φc＞φe＞φf＞φa＝φb.将电荷在各点间的移动过程转化为电荷在电场线MN上移动的情况进行分析.根据“电势顺线低”可知φM＞φN,如图6所示.

图6

a点附近等势线比b点的稀疏,故a点的场强比b点的小,选项A 错误.c点电势低于d点,正电荷从c点移到d点,即正电荷向高电势处移动,等效于正电荷由N点向M点移动,由于正电荷受力指向N点,故电场力做负功,选项B 错误.a点电势低于c点,负电荷从a点移到c点,即把负电荷移向高电势,等效于负电荷由N点向M点移动,由于负电荷受力指向M点,所以电场力做正功,选项C 正确.从e到f,电势先变低后变高,故沿此方向移动正电荷,等效于正电荷先由M移动到N,再由N移动到M,由于正电荷受力指向N点,电场力先做正功,后做负功,电势能先减小后增大,选项D 正确.答案为C、D.

3 “有迹可循”中的“电场线法”

带电粒子在电场中运动轨迹问题我们可以称之为“有迹可循”题型.结合其运动情况,对电场相关问题进行综合分析是近年来经常考查的题型.

根据牛顿运动定律可知,力是改变物体运动状态的原因,因此结合物体的运动轨迹,我们可以对物体进行受力分析,从中找出相关受力情况,从而进一步得出各方面的信息.要做到“有迹可循”,首先要画出与轨迹相交的电场线,然后结合“电场线法”相关知识进行分析.

“有迹可循”相关问题的分析方法,总结如下:1)根据题目信息,确定电场线与轨迹的交点(若题目中给出的是等势线,则可以根据电场线与等势线垂直的特点画出电场线);2)以交点作为研究对象,通过轨迹的弯曲方向判断受力方向,需要注意电场力方向需要满足两个特点:一是电场力方向与电场线的切线方向平行,二是电场力指向轨迹弯曲内侧;3)如果已知电场力的方向,则可根据带电粒子的电性判断电场的方向,或者根据电场的方向判断带电粒子的电性;4)根据“场强看疏密,电势顺线低”来判断电场强度的大小和电势的高低;5)结合轨迹,根据速度方向与静电力的方向,确定静电力做功的正负,从而确定电势能、电势和电势差的变化等;6)根据动能定理或能量守恒定律判断动能的变化情况.

例5如图7所示,虚线a、b、c是电场中的三个等势面,相邻等势面间的电势差相同,实线为一个带正电的质点仅在电场力作用下,通过该区域的运动轨迹,P、Q是轨迹上的两点.下列说法正确的是( ).

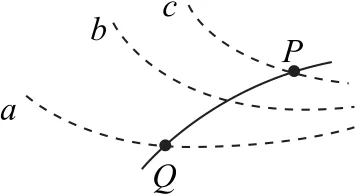
图7

A.三个等势面中,等势面a的电势最高

B.带电质点一定是从P点向Q点运动

C.带电质点通过P点时的加速度比通过Q点时小

D.带电质点通过P点时的动能比通过Q点时小

根据“电场线与等势面垂直”的特点画出一根电场线MN,并与等势面b和轨迹PQ交于S点,如图8所示,对处于S点的电荷进行分析,可得如下结论.

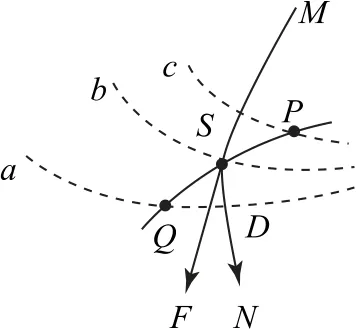
图8

因为PQ为曲线,根据其运动规律可知电荷受力方向指向曲线内侧;又因为电场力方向在电场线的切线方向上,故可确定S点的电荷受力方向如图8所示.该电荷为正电荷,受力方向与电场强度方向相同,可知电场方向由M指向N.根据“电势顺线低”可知φc＞φb＞φa,进而得出φP＞φQ.故选项A 错误.

根据“场强看疏密”可知EP＞EQ,则可知电荷在P、Q两点受力情况为FP＞FQ.结合牛顿第二定律可知其加速度情况aP＞aQ,故选项C错误.

题目中没有给出电荷的运动方向,但是可以假设若正电荷从P点移动到Q点,电势降低,借助“电场线法”,如图9所示,等效于正电荷从M点移到N点,电场力做正功,电势能减小,动能增大,即电荷在P点电势能较大,但动能较小,故选项B 错误,选项D 正确.综合以上分析可知答案为D.

图9

例6(2018年天津卷)如图10所示,实线表示某电场的电场线(方向未标出),虚线是一带负电的粒子只在电场力作用下的运动轨迹,设M点和N点的电势分别为φM、φN,粒子在M点和N点时加速度大小分别为aM、aN,速度大小分别为vM、vN,电势能分别为EpM、EpN.下列判断正确的是( ).

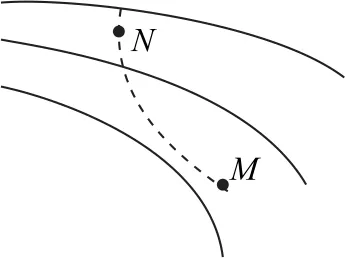
图10

A.vM＜vN,aM＜aN

B.vM＜vN,φM＜φN

C.φM＜φN,EpM＜EpN

D.aM＜aN,EpM＜EpN

带电粒子所受的电场力指向运动轨迹曲线的凹侧,又因为粒子带负电,所以电场线方向向左,根据沿着电场线方向电势逐渐降低,知M点电势高于N点电势,故选项B、C错误;又因为粒子带负电,所以粒子在M点电势能小于在N点的电势能,在M点的速度大于在N点的速度,故选项A 错误;电场线的疏密表示电场强度的大小,所以N点的电场强度大于M点的电场强度,粒子在N点的加速度大于在M点的加速度.综上所述可知选项D 正确.

4 小结

通过以上例题分析,可以看出结合电场线特点、电荷运动规律、功能关系等知识,在处理静电场综合问题时,巧妙运用“电场线法”,将会使我们的解题思路更清晰,达到事半功倍的效果.

(完)