利用“弦长公式”巧解带电粒子有界磁场问题

尹建刚

(贵州省兴义市第五中学)

带电粒子在磁场中的运动是高中物理教学中重难点内容之一,而有界磁场问题更是难点中的难点.带电粒子在磁场中的运动问题,对学生的数学能力有着较高的要求,学生普遍反映解题难度较大.本文通过几何圆半径和弦长的关系,巧妙构建“弦长公式”解题方法,思路清晰、操作简单,可有效规避传统解题方法中“定圆心”“找半径”等复杂几何关系,提高解题效率,达到事半功倍的效果.

1 “弦长公式”简介

如图1所示,设圆弧半径为R,弦AB长为l,圆心角为θ,弦切角为α,速度偏转角为φ,由几何知识有2α＝θ＝φ,则,故,得弦长AB为l＝2Rsinα,此即弦长公式.带电粒子在磁场中运动的轨道半径,则弦长表达式为.

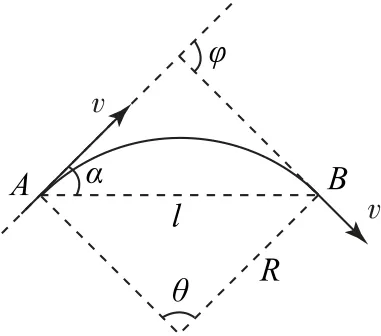
图1

2 典型例题分析

2.1 利用弦长公式直接求质量

例1如图2所示,在垂直于纸面向外且分布在x轴上方的匀强磁场中,两质量不同而电荷量相同的粒子,从O点以相同的速度沿与x轴正方向成α＝60°角射入x轴上方磁场,从a点射出磁场的粒子的质量为m1,从b点射出磁场的粒子的质量为m2.若另一与上述两质量不同而电荷量相同的粒子以相同速率与x轴正方向成α＝30°角从O点射入x轴上方磁场,从ab的中点c射出磁场(重力作用不计),则该粒子质量为( ).

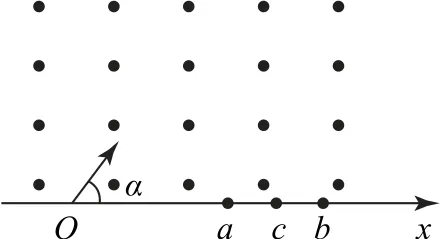
图2

根据题干条件,由弦长公式可知

由几何关系有

选项D 正确.

2.2 利用弦长公式直接求比荷

例2如图3所示,匀强磁场分布在直角三角形OPN区域内,方向垂直于纸面向外,磁感应强度大小为B.一带正电的粒子经电压U加速后从静止开始运动,沿平行于x轴方向射入磁场;一段时间后沿着垂直于x轴的方向在OP边上某点射出.坐标原点为O点,N点在y轴上,OP与x轴的夹角为30°,不计粒子重力,已知粒子离开磁场的出射点与进入磁场的入射点之间的距离为d.求:带电粒子的比荷.

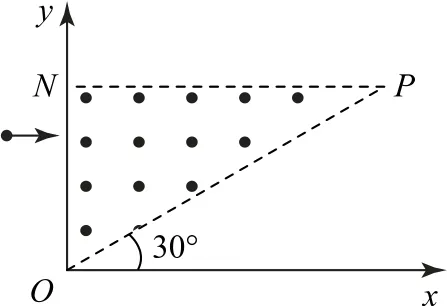
图3

如图4所示,设带电粒子的质量为m,电荷量为q,加速后的速度大小为v.由动能定理有,得

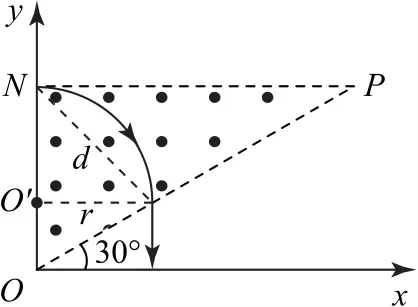
图4

由速度偏转角等于弦切角的2倍,可以推出弦切角为45°,由弦长公式有,得

2.3 利用弦长公式直接求磁感应强度

例3如图5所示,两相对放置的竖直挡板,长度、间距均为l,同一水平面上的M点和P点位于挡板边缘处,在该水平面上方分布有一匀强电场,方向竖直向下,电场强度大小为E;两挡板间有一大小可调节的匀强磁场,方向垂直纸面向外.一电荷量为q(q＞0)、质量为m的粒子以大小为v0的速度从电场中某处水平向右进入匀强电场,然后恰好从P点处进入匀强磁场,运动过程中挡板与粒子没有发生碰撞,从边缘Q和N间射出磁场.粒子射入磁场时的速度方向与PQ的夹角为60°,粒子重力大小不计.求:

图5

(1)P点到发射位置的距离;

(2)磁感应强度大小的取值范围.

(1)把进入磁场的速度分解为水平方向上的v0和竖直方向上的vy,由几何知识有.由牛顿第二定律有Eq＝ma,在竖直方向上有,vy＝at,在水平方向上有x＝v0t,联立上述各式得P点到发射位置的距离

(2)如图6所示,由题意知,当带电粒子从P点进入磁场从Q点射出磁场时,由粒子射入磁场时的速度方向与PQ的夹角为60°,知此时弦切角为60°,弦长lPQ＝l,由(1)问得入射速度,再由弦长公式直接表示为,得.

当带电粒子从P点进入磁场从N点射出磁场时,由几何关系知弦切角为15°,弦长,代入弦长公式有,其中

将之代入上面的表达式化简得

磁感应强度大小的取值范围为B1＜B＜B2,即

3 总结

综上所述,在有界磁场中,“弦长公式”为学生解决问题提供了一种很好的思路.运用“弦长公式”法,只需要知道粒子进入有界磁场的“进场点”和“出场点”,再借助圆心角、速度偏转角关系找到弦切角,最后通过简单的数学关系就可以直接求解相关的物理量,从而有效规避常规解题步骤中“画轨迹”“定圆心”“找半径”“找相关物理量”“列方程”等相对复杂的操作,大幅简化解题步骤,提高解题效率.“弦长公式”法是一种值得大力推广的好思路、好办法.

(完)