湿C 矢量及其应用*

黄逸飞 姚秀萍

1.中国气象科学研究院，北京，100081

2.中国气象局气象干部培训学院，北京，100081

1 引 言

C矢量（C）是由Xu（1992）基于准地转理论提出的、表征三维非地转运动的诊断量。准地转理论表明，气压场和风场在各自发展的同时能基本满足地转平衡，天气系统的发生、发展和消亡可归结于地转平衡的不断破坏和重建（Sutcliffe，1947）。地转平衡被破坏后，就会激发出非地转运动，非地转运动调节风场和气压场使大气运动重新恢复地转平衡。非地转运动是准地转理论的基本前提，尽管强度很弱，但它对大气运动的发展和演变至关重要（Rochette，et al，2006）。因此，诊断非地转风为构建天气系统的概念模型和识别这些系统的动力特征提供了一种行之有效的方法（Keyser，1999）。

非地转运动包括水平非地转运动和垂直运动。其中，前者可以根据观测到的风场和气压场的分布直接确定，但垂直运动由于观测手段始终无法直接获取，需要结合大气运动方程组进行计算。在准地转运动下，垂直运动的产生是为了恢复被破坏的热成风平衡。对于热成风平衡破坏的原因，准地转ω方程归结为绝对涡度平流在垂直方向上非一致性和温度平流的拉普拉斯项的共同作用（Holton，1979）。由于准地转ω方程是在地转风近似的条件下得到的，因此只需要位势场的资料即可计算垂直速度的大小。但在中性层结和不稳定层结（σ≤0）中，方程将失效（Yuan，et al，2014）。此外，准地转ω方程等号右端的两个强迫项存在互相抵消的情况，导致不易准确计算垂直速度的大小（Hoskins，et al，1978）。Hoskins 等（1978）基于地转强迫对热成风平衡的破坏作用和非地转运动对热成风平衡的重建作用，提出了一个新的物理量即Q矢量（Q），以Q的散度唯一地表示垂直运动，解决了这一问题。Q也因此被誉为计算垂直速度的先进方法（Dunn，1991）。此后，大量研究利用Q进行诊断应用的同时将其形式向更贴近实际大气运动的方向发展，逐渐完善了Q的理论分析和应用方法（张兴旺，1998，1999；Jusem，et al，1998；Yao，et al，2004；Yang，et al，2007；Riemer，et al，2014）。

不过，Q的发展在形式上始终是二维的，且丢失了非地转运动的正压部分信息，因此Q不能完整地描述三维非地转运动的分布和变化特征（Xu，1992）。Xu（1992）将Q向三维空间延伸，提出了C。其中，C的水平分量（Chor）与Q相似，相当于Q水平向右旋转90°（Chor=Q×k），二者的物理意义基本一致；C的垂直分量（C3）恢复了被Q丢失的非地转运动信息。

相较Q，C更完整地包含了三维非地转运动信息。然而，现有研究对C的关注程度远不如Q。Chu（2002）利用C诊断了弗拉姆海峡中的海洋次级环流的分布特征，而迄今为止，没有研究将C应用于气象学中。此外，相较Yao 等（2004）引入凝结潜热提出的湿Q矢量（Q*），C仍是基于地转风近似和绝热条件下得到的，既没有描述非地转强迫效应，也没有包含大气中的非绝热过程所产生的非地转运动，从而难以更真实地描述大气中的降水及其影响天气系统的发生、发展过程。本研究在Q和C的基础上，从β平面近似下的p坐标系原始方程组出发，考虑与水汽有关的非绝热效应，得到了湿C矢量（C*）。给出了C*的表达式并揭示C*的物理意义，通过一个青藏高原低涡（以下简称“高原涡”）的诊断展示了C*的应用价值。

2 C*的表达式及其物理意义

2.1 C＊的表达式

C*的表达式如下（详细推导参见附录）

2.2 C＊的物理意义

2.2.1C*水平分量的物理意义

若取f平面近似，可从式（4）中略去此时的与Yao 等（2004）在f平面近似下得到的湿Q矢量（Q*）满足=Q*×k的关系（在p坐标系下， k指向-p方向）。实际上，文中推导所用的方式与Q*基本一致，但进一步考虑了纬度的变化，理论上比Q*更精确。包含了Q*的全部信息，Q*分析方法可完全由代替。例如，根据与非地转运动的关系（附录式（A21）与式（A22）），还可以得到以C*表征的ω方程

式中，ω为p坐标系下的垂直速度，为p坐标系下的水平哈密顿算子。可见，的涡度可以唯一地表征垂直运动，其与Q*的散度等价。对于而言，上升运动发生于其指向方向的左侧，下沉运动位于其指向方向的右侧；此外，气旋式旋转对应上升气流，而其反气旋式旋转对应下沉气流。

式（4）表明，产生次级环流的强迫共有3 项，分别如下

式中，为f平面上的热成风非平衡项，为β效应项，为非绝热加热项。接下来分析上述3 项的物理意义。

表征了破坏热成风平衡的水平形变强迫（图1）。图1a 所示的水平伸缩形变在加强经向位温梯度的同时也减弱了水平拟涡度，从而破坏了热成风平衡。其中热成风非平衡的热力部分可以表示为即单位时间（δt）内伸缩形变造成的经向位温梯度加强；热成风非平衡的动力部分可以表示为即单位时间（δt）内伸缩形变造成的水平拟涡度减弱。热成风非平衡的热力部分产生净浮力Fb，导致南侧出现上升运动、北侧出现下沉运动；热成风非平衡的动力部分产生科里奥利力Fc，出现低层向南、高层向北的水平非地转运动，与热力部分产生的垂直运动一起构成次级环流。次级环流具有减弱经向位温梯度和增加水平拟涡度的作用，能够恢复被破坏的热成风平衡。因此，也能够表示这一次级环流（与次级环流的关系式参见附录）。

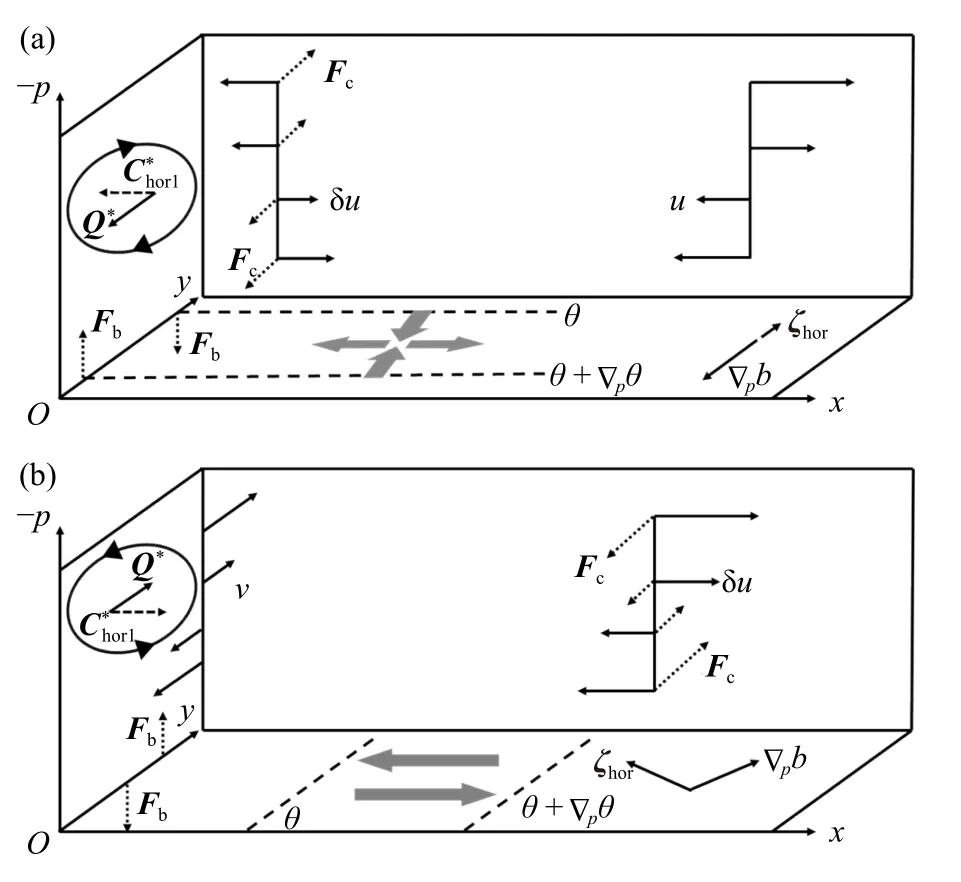
图1 水平伸缩形变 （a） 和切变形变 （b） 破坏热成风平衡产生次级环流的机理示意 （底部虚线为等位温线，灰色粗箭头分别表示伸缩形变和切变形变；形变强迫改变位温梯度和水平拟涡度 （ζhor），破坏热成风平衡；Fb 和 ∇pb 分别为位温梯度改变产生的净浮力和对应的净浮力梯度；δu 和Fc 分别为热成风非平衡改变的水平拟涡度以及对应的科里奥利力；净浮力和科里奥利力产生了次级环流，可分别用Q*和表示）Fig.1 Schematic diagram of the mechanism behind the horizontal telescoping deformation （a） and shearing deformation （b） destroying the thermal wind balance （the dashed lines at bottom are isotherms，and the gray thick arrows indicate the telescoping and shearing deformation；the deformation force changes the potential temperature gradient and the horizontal pseudovorticity （ζhor），and destroys the thermal wind balance；Fb and ∇pb are the net buoyancy and related buoyancy gradient generated by the change of the potential temperature gradient；δu and Fc are the horizontal pseudovorticity and related Coriolis force changed by the thermal wind imbalance；the secondary circulation is generated by both the net buoyancy and Coriolis force，and can be represented by Q* and respectively）

图1b 所示的水平切变形变改变了纬向位温梯度和纬向水平拟涡度，并在经向上产生位温梯度和水平拟涡度，从而破坏了热成风平衡。其中热成风非平衡的热力部分可以表示为即单位时间（δt）内切变形变产生的经向位温梯度；热成风非平衡的动力部分可以表示为即单位时间（δt）内切变形变产生的水平拟涡度。热成风非平衡的热力部分会产生净浮力Fb，导致南侧出现下沉运动、北侧出现上升运动；热成风非平衡的动力部分会产生科里奥利力Fc，出现低层向北、高层向南的水平非地转运动，与热力部分产生的垂直运动一起构成了次级环流。综上所述，具有两层含义：破坏热成风平衡的形变强迫以及恢复热成风平衡的次级环流。此外，若不考虑纬度变化和非绝热加热作用，同时以地转风代替实际风，则与Xu（1992）的Chor完全等价，因此二者的物理意义是相似的。

实际上，由形变强迫破坏热成风平衡、产生次级环流是锋生的典型机制。这一机制除了可以由Q和C予以解释外，也包含在Sawyer-Eliassen 方程中（Sawyer，1956；Eliassen，1962）。其中的Sawyer-Eliassen 方程、Hoskins 等（1978）提出的Q和Xu（1992）提出的C分别是在半地转和准地转近似的条件下讨论上述过程；而Davies-Jones（1991）引入拟涡度的概念讨论热成风平衡破坏的机制，将Q推广至原始方程组，得到了广义Q矢量。从原始方程组中得到的C*则同时包含了地转强迫和非地转强迫，理论上比C更精确。

揭示了β效应破坏热成风平衡并产生次级环流的机制。将表达式代入式（5）ω方程等号右端，并代入热成风关系可得

可见，取β平面近似为ω方程增加了一个额外的强迫项。仍以北半球中纬度地区为例，设想存在一个振幅较大的温度槽，温度槽东、西两侧的位温梯度近似纬向分布。温度槽西侧为偏北热成风，存在上升运动；温度槽东侧为偏南热成风，存在下沉运动。由此，和描述了β平面上破坏热成风平衡的大气运动强迫以及为恢复热成风平衡所产生的次级环流。

描述了水平方向上非绝热效应分布不均产生的次级环流，即非绝热效应分布不均改变了水平位温梯度和水平风的垂直切变，由此出现了次级环流。其形式较为简单，且物理意义明晰。

综上所述，描述的次级环流实际由两种强迫产生：β平面上的热成风非平衡作用和非绝热加热作用。

2.2.2C*垂直分量的物理意义在揭示所表征的大气运动强迫作用的物理

水平非地转运动来自气压梯度力与科里奥利力的不平衡，即

式中， ϕ为位势。将式（11）乘以f0后做、将式（12）乘以f0后做后再相减，可得

若运动是地转平衡的，式（13）等号右端括号内为0，因此式（13）表征了地转非平衡状态下大气通过水平旋转的非地转运动以恢复地转平衡。

将β平面近似下的地转关系（fVg=-∇pϕ×k）代入式（13）等号右端替换 ϕ，再代入式（10）并展开可得

可见，式（14）等号右端的中括号内第1 项对应，表明的是形变和旋转强迫产生的非地转垂直涡度；与类似，也是取β平面近似后出现的额外强迫，揭示了β平面上地转风在经向上的非一致性而出现的地转非平衡状态。

揭示了f平面上水平运动强迫对地转平衡的破坏，具体而言，包含水平形变强迫和水平旋转强迫。实际上，若以地转风代替水平运动，其退化为Xu（1992）的C3。因此，的物理意义与C3相似。图2 展示了上述两种强迫对地转平衡的破坏以及产生非地转运动的机理，与Xu（1992）的图4 相似。在图2a 所示的水平伸缩形变中，水平运动在收缩轴上辐合、在伸展轴上辐散，动量的平流作用破坏了地转平衡。其中，地转非平衡可以表示为δV=-(V•∇pV)•i=-α2rδt（其中r为到形变中心的径向距离），即单位时间δt内由地转风形变引起的径向向内的运动，其对应的科里奥利力Fc呈气旋式旋转。在Fc的作用下出现了气旋式旋转的非地转运动。在图2b 所示的气旋式水平旋转中，产生径向向外的惯性离心力破坏了地转平衡，地转非平衡可表示为（其中r为到旋转中心的径向距离），即单位时间δt内由水平旋转引起的惯性离心力所产生的径向向外的运动，其对应的科里奥利力Fc呈反气旋式旋转。在Fc的作用下出现了反气旋式旋转的非地转运动。

图2 水平形变 （a） 和旋转 （b） 破坏地转平衡产生非地转运动的机理示意 （粗箭头分别表示形变和旋转，细箭头和虚线箭头分别为地转非平衡产生的水平运动 （δV） 及其对应的科里奥利力 （Fc））Fig.2 Schematic diagram of the mechanism behind the horizontal deformation （a） and rotation （b） destroying the geostrophic balance （the thick arrows indicate the deformation and rotation respectively，and the thin and dashed arrows indicate the horizontal motion （ δV） and related Coriolis force （ Fc）respectively）

为β效应项，文中以一个简单的假设揭示该项的机理。仍以北半球为例，假设高空存在一个圆形的大尺度低压涡旋系统，其内部的位势梯度在各方向上都是均匀的。此时f0由涡旋中心所在的纬度值确定，涡旋中心所在纬圈上y=0。从涡旋中心出发，分别向北和向南确定两个点A和B，二者与涡旋中心的距离均为y（图3）。显然，A点的地转风强度和地转风涡度均小于B点。由于A点位于涡旋中心北侧，根据式（16），在A点有＜0，根据式（13），A点的地转非平衡可表示为其中 ζA和 ϕA分别为A点的垂直相对涡度和位势；而B点位于涡旋中心南侧，＞0，因此B点的地转非平衡可表示为其 中 ζB和 ϕB分 别 为B点的垂直相对涡度和位势。可见，β效应使低压涡旋北部出现次地转风，低压涡旋南部出现超地转风。因此，随着时间推移，在涡旋的东半部分，会因为质量堆积出现辐合，而涡旋的西半部分的情况正好相反。因此，对于北半球而言，β效应项使大尺度低压涡旋系统向西移动。

图3 β 效应破坏地转平衡的机理示意 （同心圆代表低压涡旋系统的等位势高度线，涡旋内位势梯度的大小一致；A 和B 为与涡旋中心处于同一经圈上的两个点，且二者与涡旋中心的纬距相等；A点的地转风涡度和地转风强度均小于B 点；A 和B 点的分别为负值和正值）Fig.3 Schematic diagram of the mechanism behind the βeffect destroying geostrophic balance （the concentric circles represent the isohypses of the low-pressure vortex system，and the magnitude of the potential gradient within the vortex is consistent；A and B are two points on the same longitude circle as the center of the vortex，and the latitudinal distances between them and the center of the vortex are equal；both the geostrophic vorticity and the geostrophic wind intensity at point A are smaller than those at point B； of A and B are negative and positive respectively）

综上所述，C*表征了大气运动的两种非平衡状态下激发的非地转运动。其中表征了由β平面上的热成风非平衡和非绝热加热作用产生的次级环流；表征了由β平面上的地转非平衡激发的水平非地转运动。

3 C*的应用

3.1 高原涡个例概况

文中利用C*诊断一个高原涡个例的形成、发展和移动过程以探讨C*的应用价值。2016 年6 月28 日，一个高原涡生成于青藏高原西部，随后向东移动并不断发展，最终移出高原，为中国东部地区带来一次强降水过程。马婷等（2020）从位涡的视角对该高原涡的形成、发展以及移出高原造成降水的过程进行了全面的分析。由于已有研究证实了Q*的散度与降水发生的区域和降水强度有很好的对应关系（姚秀萍等，2001），而根据前述与Q*的关系，不难推断出的旋度具有与Q*的散度同等的应用价值。因此，文中不对该高原涡造成降水的过程进行诊断，仅利用C*分析高原涡在高原上的演变过程。计算C*所用数据为第5 代大气再分析资料（ERA5）（Hersbach，et al，2020），空间分辨率为1°×1°。该高原涡的演变过程、中心位置和强度变化等要素来自高原涡数据集（林志强等，2022），该数据集是基于高原涡的客观识别方法建立的（Lin，2015；Lin，et al，2020）。

图4 给出了高原涡形成、发展过程中500 hPa高度上高原涡中心的位置和移动路径以及高原涡中心的位势高度和垂直相对涡度的变化。6 月28 日12 时（世界时，下同），高原涡在高原西部形成并东移发展，其中在29 日00 时前主要向东偏北方向移动；29 日00 时后，高原涡转向东南方向移动并在30 日00 时移出高原（图4a）。分析高原涡中心的气压场和风场发现，高原涡在形成后首先减弱，对应位势高度增大和垂直相对涡度减小；28 日16 时后，位势高度开始减小，表明低压加强，但这一时段垂直相对涡度亦减小，二者的变化趋势导致高原涡中心的地转非平衡加强。29 日00 时后，虽然高原涡中心的低压变化并不明显，但此时垂直相对涡度显著增大，表明风场加强旋转以对应已经加强的低压，减弱了地转非平衡的程度。06 时后低压强度又有所增强，但风场旋转减弱；12 时低压强度减弱但风场旋转增强。此后低压持续发展至高原涡移出高原，而垂直相对涡度的强度仍发生波动变化（图4b）。总体而言，高原涡中心的垂直相对涡度的变化滞后于位势高度。接下来利用C*对高原涡的上述演变过程进行分析。

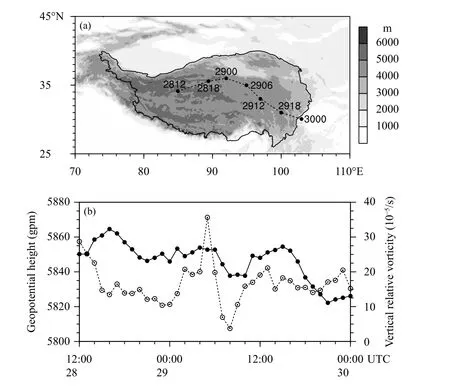
图4 2016 年6 月28 日12 时至30 日00 时500 hPa 高度上高原涡中心的位置和移动路径（a） （图中数字前两位为日、后两位为时；黑色实线为青藏高原边界，灰阶为海拔高度） 以及 （b） 其位势高度 （实线） 和垂直相对涡度 （虚线） 的演变Fig.4 （a） The track of the Qingzang plateau vortex center at 500 hPa from 12:00 UTC 28 June to 00:00 UTC 30 June 2016（the black line is the boundary of the Qingzang plateau and the altitude is shaded；the number is date （day） and time （hour）），and （b）evolution of the geopotential height of the vortex center （solid line） and vertical relative vorticity （dashed line）

3.2 C＊的分布和变化特征

图5 给出了C*在高原涡形成和发展过程的分布和变化特征。6 月28 日06 时，即高原涡形成前6 h，在未来高原涡形成的区域处存在一个大尺度的低压槽，槽区的强度较弱，表明此时次级环流并不明显。同时，槽区内基本为正值，表明该处垂直相对涡度大于地转风涡度（图5a）。12 时高原涡形成，其中心位于一个范围较大的闭合低压内。显著增强，且高原涡中心及其东侧存在明显的逆时针旋转的，指示了上升运动的存在。高原涡中心及其附近较大范围内均为正值，表明高原涡中心处于地转非平衡状态，且垂直相对涡度相对于低压更强（图5b）。的这一特征对应了图4b 中高原涡形成后强度首先减弱的趋势。28 日18 时，高原涡中心东移并发展，此时在高原涡中心北侧一致地指向偏南方，且在高原涡东侧表现出显著的逆时针旋转特征，表明上升运动处于高原涡中心东侧。此外，高原涡中心的已转变为负值并形成了一个负值中心，表明此时的地转非平衡状态需要风场加强气旋式旋转（图5c）。29 日00 时，气旋式旋转的区域位于高原涡中心及其东侧，而反气旋式旋转的区域位于高原涡中心西侧，表明此时出现了一个在高原涡东侧上升、西侧下沉的次级环流。同时，高原涡中心附近的负值中心加强，体现了图4b 中表征的地转非平衡程度加深，但负值中心与高原涡中心并未完全重合。此外，此时高原涡中心所在纬度达到最大（图5d）。此后，高原涡向东南方移动，且高原涡中心的垂直相对涡度迅速增大，地转非平衡程度减弱，因此在29 日06 时，对应高原涡中心的负值中心强度有所减弱。同时，高原涡中心的转为一致指向西的特征，且高原涡中心南侧和西北侧分别存在气旋式和反气旋式旋转的，表明上升运动和下沉运动分别发生于高原涡中心的南侧和西北侧（图5e）。上述分析表明，揭示了高原涡中心移动方向改变的原因。在29 日00 时以前，上升运动均位于高原涡中心的东侧，使高原涡在该时段内向偏东方向移动；00 时以后，上升运动发生于高原涡中心的南侧，由于高原涡所在的背景气流为西风，因此高原涡最终向东南方向移动和发展，直至移出高原。因此，之后位于高原涡中心及其附近的几乎均表现为指向西方的特征，并且气旋式和反气旋式的均位于高原涡中心的南、北两侧（图5f—h）。同时，对应于高原涡中心的负值中心也在加强，使高原涡中心的垂直相对涡度进一步增大，预示了高原涡的发展。此外，在高原涡移出高原时，负值中心强度显著减弱，表征高原涡移出高原后有向低层发展的趋势，此时涡管伸长，导致低层旋转加强，此时明显的负值中心应见于较低的高度上。同时，高原涡东北方向的低压槽内存在明显的负值中心，表明该低压槽在移出高原后将进一步发展（图5h）。

图5 2016 年6 月28 日06 时至30 日00 时500 hPa 高度上逐6 h 的 （箭矢，单位：10-10 s-3）、 （色阶，单位：10-13 s-3） 和位势高度 （等值线，单位：gpm） 的分布 （红色三角代表高原涡中心位置，灰色实线为青藏高原边界）Fig.5 Distributions of （vector，unit：10-10 s-3）， （shaded，unit：10-13 s-3） and geopotential height （contour，unit：gpm） every 6 h from 12:00 UTC 28 June to 00:00 UTC 30 June 2016 （the red triangle represents the location of the Qingzang plateau vortex center，and the gray line is the boundary of the Qingzang plateau）

综上所述，和在高原涡的演变过程中分别具有如下分布和变化特征：在高原涡中心由指向偏南方向转变为指向偏西方向，表征了上升运动的位置从高原涡中心东侧移动至高原涡中心南侧，从而揭示了高原涡移动方向的改变。由于与Q*包含的非地转运动信息相同，因此使用Q*诊断也能够得到同样的结果。而作为对Q*的补充，其负值中心与高原涡中心有较好的对应关系，且负值中心的强度变化与高原涡中心强度变化表现一致，可以表征高原涡的发展。此外，对比马婷等（2020）的位涡诊断研究可以发现，高原涡中心虽然处于高位涡区域内，但高位涡表现为一带状区域；相比之下，的负值中心能够更好地表征高原涡中心的位置，可作为追踪高原涡移动路径的指示因子。

此外，从该高原涡个例的诊断可以发现，比大3 个量级左右。这样的结果一方面说明高原涡个例的形成和发展以热成风非平衡和非绝热加热为主，地转非平衡的作用很弱，即非地转运动主要表现为次级环流，水平非地转风的旋转强度很小；另一方面，虽然的量级不大，但其负值中心能够指示高原涡中心的位置并预示高原涡的强度变化。因此，作为对Q分析方法的补充，有助于在二维等压面上确定高原涡中心的位置以及判断高原涡的演变趋势，具有较大的应用价值。

若采用Xu（1992）基于准地转近似得到的C对上述过程进行诊断，即不考虑非绝热效应和纬度变化，并以地转风替代实际风，则存在明显的局限性。图6 展示了C在上述高原涡形成和发展过程中的分布和变化特征。相较于C*，C存在3 个方面的不足。首先，Chor的强度大约只有的一半，因此由C表征的次级环流的强度只有C*的一半，这会导致计算出的垂直速度显著偏小。其次，在高原涡形成、发展和移动的过程中，高原涡中心附近的Chor几乎总是指向偏南，并非如存在显著的方向改变。这使得Chor表征的上升运动几乎始终位于高原涡中心的偏东方向，难以解释高原涡移动方向发生明显变化。最后，C3的量级明显大于，使得C3与Chor只相差约2 个量级，这使得利用C进行诊断时会高估地转平衡破坏和重建的作用。同时，C3的强度变化在29 日00 时前后显著小于，所表征的地转非平衡程度的加深不如。此外，高原涡移出高原后，其中心附近的C3负值中心仍然较强，对表征低层旋转加强的作用亦不如。

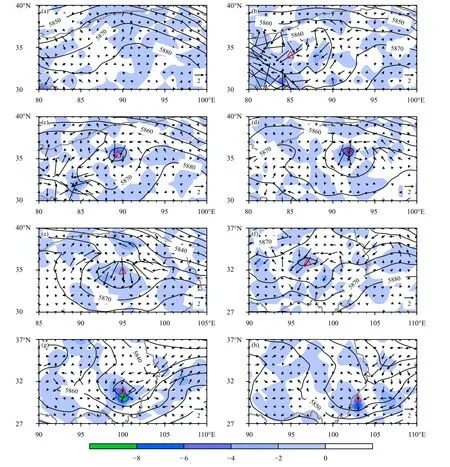
图6 同图5，但为Chor （箭矢，单位：10-10 s-3）、C3 （色阶，单位：10-12 s-3） 的分布Fig.6 Same as Fig.5 but for the distributions of Chor （vector，unit：10-10 s-3） and C3 （shaded，unit：10-12 s-3）

为了进一步探究C*和C差异的成因，将C*进一步分解为3 个部分：f平面上的热成风非平衡以及 地 转 非 平 衡 部 分（和）、β效 应 部 分（和）和非绝热加热部分（），分别利用上述3 部分对该高原涡进行诊断（图略）。结果表明，考虑非地转强迫的热成风非平衡和地转非平衡作用是造成二者差距的主要原因，也是高原涡移动方向发生变化的主导因素。非绝热加热作用虽然也影响高原涡移动的方向，但该项强度只有前者的一半，相对贡献较小。β效应的强度相较于前两者大约小1 个量级，对高原涡的演变作用可忽略不计。可见，C*能够描述更准确的非地转运动，在应用中具有显著优势。

4 结论和讨论

基于Xu（1992）提出的C，从p坐标系下的原始方程组出发，考虑β平面近似和包含水汽作用的非绝热加热效应，推导出C*，并利用C*诊断了一个高原涡。得到如下结论：

（1）C*体现了更完整的非地转运动。其中，C*的水平分量表示由 β平面上热成风平衡破坏和非绝热加热的作用产生的次级环流；C*的垂直分量恢复了被Q丢失的非地转运动信息，表示由β平面上地转平衡破坏产生的非地转运动。

（2）相较于C，C*对高原涡形成、发展和移动过程有更好的指示作用。C*的诊断结果表明，上升运动的位置从高原涡中心东侧转为高原涡中心南侧，导致高原涡移动方向由偏东转为东南。负值中心的位置与高原涡中心对应较好，并且负值中心的强度变化对高原涡的发展具有一定的指示作用。作为Q的补充，具有较显著的应用价值。

（3）和的相对大小还表明高原涡存在显著的斜压性。在高原涡的演变过程中，比大3 个量级，表明热成风平衡的破坏和恢复远大于地转平衡的破坏和恢复，因此高原涡的演变以斜压过程为主。

文中对C相关研究进行了理论发展，得到了C*表达式，发现了C*的应用价值。以实际运动代替地转风并引入β平面近似和凝结潜热作用，得到了能描述更完整的非地转运动的C*。不过，由于C*的推导过程中采取了替换平衡近似（参见附录），从而滤去了惯性重力波，因此C*的诊断对象需要具有较小罗斯贝数的动力特征（Davies-Jones，1991）。鉴于可能具有指示天气系统位置和预示天气系统发展的作用，未来的研究可尝试将作为追踪天气尺度低涡系统中心位置和预测其演变的参考因子，也许能更进一步发掘C*潜在的应用价值。

附 录

C＊的推导

取β平面近似，准静力平衡、无摩擦、考虑非绝热效应的p坐标系下的原始方程组为

式中，ua和va为水平非地转运动，ω为垂直速度，为比容，θ为位温，，L为水汽凝结潜热，为定压比热，R为比气体常数，qs为饱和比湿，β=df/dy，f0由所选择的研究区域的中心纬度给定，y为实际应用中选取的研究区域内各点相对于研究区域中心的经向位移。

分别对式（A1）、（A2）乘以f0后做得

根据位温的定义和状态方程，可将位温改写为以下形式

对于天气尺度的大气运动而言， ϕ在水平和垂直方向都是连续的，因此上式等号左端 ϕ的微分可以互换顺序。注意到地转关系，可将其改写为

重复以上步骤，式（A9）可改写为

根据替换平衡近似（Dutton，1976），式（A14）和（A15）等号左端均为0。将上述两式中含非地转风垂直切变项和垂直运动水平切变项移至等号左端并在等号两端同时乘以h得

式中，

分别对式（A1）和（A2）乘以f0后做和并相加

式中，D为散度，ζg为地转风涡度，Vh为二维水平运动。

式（A22）与水平散度方程形式相似。在大尺度运动下，对上式各项做尺度分析，有

因此，略去式（A22）中的小项并乘1/2，可得

式中，

为了描述大气运动中形变、旋转和辐合/辐散作用的强度，分别有形变拟能（σe）、涡度拟能（εe）和散度拟能（δe）（高守亭等，2015）

将上述拟能表达式代入式（A23）等号右端并略去量级较小的散度拟能项，可得

式（A18）、（A19）和（A28）即为C*三个分量的表达式。