Matlab在二元完全理想系相平衡关系计算中的应用
黄英虎,农正东,邢靓,郭效瑛,李素萍,马理,李伟
(百色学院化学与环境工程学院,广西 百色 533000)
精馏作为一种典型的分离单元操作,其设计计算在化工计算中尤为重要。在精馏塔的逐板计算中,相平衡关系的计算因涉及非线性方程(组)的求解,计算繁琐,是全过程中最难穿越的“荆棘”,导致本就复杂的计算过程愈加困难[1-2]。因此,精馏计算常需依托软件编程来完成。在众多的编程软件中,Matlab因其数值计算功能卓异、库函数浩博、语言简易、语法灵活、易于可视化等优势而脱颖而出,为化工计算提供了极大的便利[3-5]。
在所有的气液两相体系中,二元完全理想系的相平衡计算最为简单。在完全理想系的相平衡关系中,相对挥发度是关键参数。在恒压精馏过程中,因其是温度的函数,所以其值会随塔板温度的变化而变化[6]。因此,确定合适的相对挥发度对精馏计算非常重要。若有相平衡实验数据,可以拟合出相对挥发度[7];反之,则需要选取合适的平均相对挥发度[8]。本文通过几何平均法、对数平均法和算术平均法求得平均相对挥发度,并将三者用于给定组成的泡露点温度、给定温度的饱和气液相组成的计算。最后以直接计算法的结果作为基准,通过相对偏差分析对三种方法进行评价。本文以Matlab 函数或脚本实现全部计算过程。
1 计算原理
1.1 饱和蒸气压的计算
组分m的饱和蒸气压可由Antoine方程[9]计算:
式中Am、Bm和Cm为组分m 的Antoine 参数;(T)为组分m于温度T(K)下的饱和蒸气压(mmHg)。
1.2 相对挥发度
当完全理想系达到相平衡时,对组分m,有:
式中,ym、xm分别为温度T(K)下组分m于饱和气液相中的摩尔分数;p(mmHg)为体系的总压,常压时,p=760 mmHg。
1.2.1 塔顶和再沸温度及另一相组成
本节采用直接计算法计算塔顶和再沸器的操作温度及未知的另一相组成。
在温度T(K)下,将式(2)应用于轻、重两组分,建立一侧归零化的方程组:
式中,y1、x1分别为饱和气液相中轻组分的摩尔分数,轻重两组分的饱和蒸气压与温度T的关系满足式(1)。为使叙述简练,下文将轻组分的摩尔分数简称为组成。
式中,xD和xW分别为塔顶和塔底产品组成,xD为给定参数,xW可由全塔物料衡算求解;TD(K)为塔顶的操作温度;xLD为自塔顶第一块理论板下降的饱和液相组成;TW(K)为再沸器的操作温度;yW为再沸器产生的饱和气相组成。
1.2.2 塔顶和塔底的相对挥发度
塔顶和再沸器操作温度下的相对挥发度可用式(4)计算:
式中,k1(T),k2(T)分别为温度T(K)下轻组分和重组分的气液平衡常数;y(T),x(T)分别为该温度下的饱和气液相组成。
取T=TD和T=TW,则可由1.2.1提及或计算出的xD[y(TD)]、xLD[x(TD)]、yW[y(TW)]、xW[x(TW)]对应计算出α(TD)和α(TW),两者分别为塔顶和再沸器操作温度下的相对挥发度。
1.2.3 平均相对挥发度
几何平均法采用式(5)计算平均相对挥发度:
对数平均法采用式(6)计算平均相对挥发度αˉlog:
算术平均法采用式(7)计算平均相对挥发度αˉari:
三种方法因都采用了相对挥发度,所以统称为相对挥发度法。在本文案例条件下,三种相对挥发度的最终计算结果分别为2.469、2.469和2.471。
1.3 相平衡方程式
式中,x为饱和液相组成;α为某一种平均相对挥发度,可由式(5)(6)或(7)求得;ye为与x同温的饱和气相组成。
1.4 泡露点温度的计算
给定组成(本文选进料组成xF)的泡露点温度可以用直接计算法和相对挥发度法来求取。
1.4.1 直接计算法
将式(9)与式(1)联立即可求出泡点温度Tb(K)
将T=Td和y1=xF代入式(3),并联立式(1)即可求出Td(K)。
1.4.2 相对挥发度法
相对挥发度法由式(10)计算Tb(K):
相对挥发度法由式(11)列出的方程组计算Td(K):
1.5 饱和气液相组成的计算
给定温度(本文选择进料温度TF,要求Tb≤TF≤Td)下的饱和气液相组成亦可由上述两类方法计算。
1.5.1 直接计算法
进料温度下的饱和液气相组成xe、ye可分别由式(12)和(13)计算:
1.5.2 相对挥发度法
相对挥发度法由式(14)列出的方程组求xe、ye
式中,(TF)为进料温度下轻组分的饱和蒸气压(mmHg),可由式(1)计算。
2 计算示例与程序
计算案例:已知苯-甲苯精馏塔的原料流量为10 kmol/h,其中苯含量为50%(摩尔分数,下同),在1 atm下进行精馏,塔顶馏出液的流量为5 kmol/h,苯含量为95%。在操作条件下,苯-甲苯可按完全理想体系进行计算。苯(1)、甲苯(2)的饱和蒸气压可由式(1)计算,其对应的Antonie参数见表1。
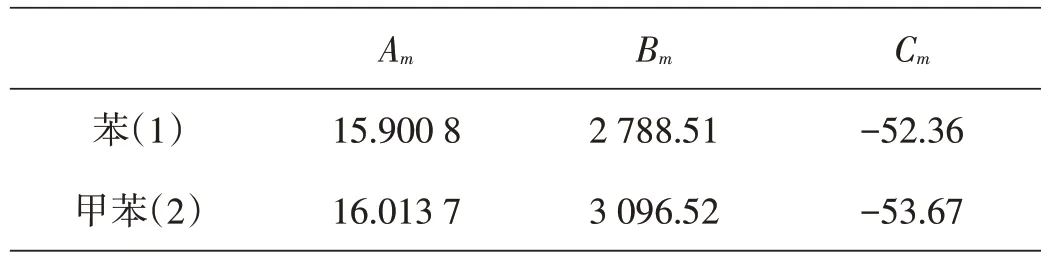
表1 苯和甲苯的Antonie参数[9]
试求:①分别以三种方法计算进料组成的泡露点温度tb和td;②在两温度间选取进料温度tF,分别以三种方法计算进料温度下的饱和气液相组成。
2.1 塔顶、再沸器的操作温度及另一相组成的计算
新建一个名为IDVLEpy的函数,该函数可用于以直接计算法计算塔顶液相组成和塔顶的操作温度,编辑代码如下:
function xt= IDVLEpy(xx)
%IDVLEpy 函数在已知压力P,塔顶气相组成xD下,返回关于饱和液相组成和塔顶操作温度的方程组
%xx 的两个元素依次为饱和液相组成xLD 和塔顶的操作温度tD(K)
global CA P xD
%以下两步以Antoine 方程计算塔顶温度下轻重两组分的饱和蒸气压列向量Ps(mmHg)
lnPs=CA(:,1)-CA(:,2)./(CA(:,3)+xx(2));
Ps=exp(lnPs);
%以下两步分别给出塔顶饱和气液相中轻重两组分的摩尔分数列向量y和x
y=[xD;1-xD];x=[xx(1);1-xx(1)];
xt=y*P-x.*Ps;%建立求解方程组,取一侧化为0后的表达式
end
新建一个名为IDVLEpx的函数,该函数可用于以直接计算法计算再沸器气相组成和再沸器的操作温度,编辑代码如下:
function yt = IDVLEpx(xx)
%IDVLEpx 函数在已知压力P,塔底再沸器液相组成xW下,返回关于饱和气相组成和再沸器的操作温度的方程组
%xx 的两个元素依次为饱和气相组成和塔底再沸器的操作温度,K
global CA P xW
%以下两步以Antoine方程计算塔底再沸器温度xx(2)(K)下轻重两组分的饱和蒸气压列向量,mmHg
lnPs=CA(:,1)-CA(:,2)./(CA(:,3)+xx(2));
Ps=exp(lnPs);
%以下两步分别给出再沸器饱和气液相中轻重两组分的摩尔分数列向量y和x
y=[xx(1);1-xx(1)];x=[xW;1-xW];
yt=y*P-x.*Ps;%建立求解方程组,取一侧化为0后的表达式
end
2.2 三种平均相对挥发度的计算
新建一个名为rvmean 的函数,可以选择几何平均法、对数平均法或算术平均法之一计算全塔轻组分对重组分的平均相对挥发度alpha,编辑代码如下:
function alpha= rvmean(xD,xW,xLD,yW,str)
% rvmean 函数以给定的方法计算全塔轻组分对重组分的平均相对挥发度alpha
%xD和xW分别为塔顶产品和塔底产品组成
%xLD 为塔顶温度下饱和液相中轻重组分的摩尔分数列向量;yW 为再沸温度下饱和气相中轻重组分的摩尔分数列向量
%str为方法判断字符串
%以下两步分别计算塔顶及再沸器操作温度下的气液平衡常数kD和kW
kD=[xD;1-xD]./xLD;kW=yW./[xW;1-xW];
%以下两步分别计算塔顶及再沸器中轻组分对重组分的相对挥发度
alpha_D=kD(1)/kD(2);alpha_W=kW(1)/kW(2);
if strcmp(str,′geo′) %几何平均值法
alpha=sqrt(alpha_D*alpha_W);
elseif strcmp(str,′log′)%对数平均值法
alpha=(alpha_D-alpha_W)/log(alpha_D/alpha_W);
elseif strcmp(str,′ari′) %算术平均值法
alpha=(alpha_D+alpha_W)/2;
end
end
2.3 泡露点温度的计算
新建一个函数命名为BPT,可为直接计算法求给定组成的泡点温度提供方程,编辑代码如下:
function fun = BPT(t)
%BPT函数返回直接计算法求泡点温度的方程
% t为待求解的给定组成的泡点温度,K
global CA P xF
%将Antoine 参数矩阵CA、总压P(mmHg),给定组成xF定义为全局变量
Ps=exp(CA(:,1)-CA(:,2).(/CA(:,3)+t));%以Antoine公式计算轻重两组分在(tK)下的饱和蒸气压列向量,mmHg
x=[xF;1-xF];%给出饱和液相中轻重两组分的摩尔分数列向量
fun=sum(x.*Ps)-P;%建立泡点温度求解方程,取一侧化为0后的表达式
end
新建一个函数命名为DPT,可为直接计算法求解给定组成的露点温度提供方程组,编辑代码如下:
function fun = DPT(xx)
%DPT 函数返回直接计算法求解露点的温度和露点液相组成的方程组
%解向量xx 的两个元素依次为露点温度下的饱和液相组成及给定组成的露点温度,K
global CA P xF
y=[xF;1-xF];%给出饱和气相中轻重两组分的摩尔分数列向量
Ps=exp(CA(:,1)-CA(:,2)./(CA(:,3)+xx(2)));%计算轻重两组分在温度xx(2)(K)下的饱和蒸气压列向量,mmHg
x=[xx(1);1-xx(1)];%给出露点温度下饱和液相中轻重两组分的摩尔分数列向量
fun=x.*Ps-y*P;%建立露点温度求解方程组,取一侧化为0后的表达式
end
编辑一个名为Tdx_rv的函数,为相对挥发度法计算露点温度提供方程组
function f= Tdx_rv(xx)
% Tdx_rv 函数返回相对挥发度法求露点温度和露点液相组成的方程组
% 解向量xx 的两个元素依次是露点液相组成xd和露点温度Td(K)
global CA P alpha xF
f(1)=xx(1)*exp(CA(1,1)-CA(1,2)/(CA(1,3)+xx(2)))-xF*P;
f(2)= alpha*xx(1)/(1+(alpha-1)*xx(1))-xF;
end
编辑一个名为BDPT_2M 的函数,可以给定的方法和参数计算泡露点温度
function [tb,td] = BDPT_2M(xF,alpha,str)
%BPT_2M函数可以用两类方法计算泡点温度,tb、td分别为待求解的给定组成的泡点及露点温度
global CA P
if strcmp(str,′dc′)
%以下两步用以求解给定组成的泡点温度
t0=95+273.15;%给出初值t0(K)
tb=fzero(@BPT,t0)-273.15;%调用fzero 函数求解tb(℃)
%以下三步用以求解给定组成的露点温度td(℃)
xx0=[xF,t0];%给出初值向量xx0
r=fsolve(@DPT,xx0);%调用fsolve 函数解DPT 函数所定义的方程组
td=r(2)-273.15;
elseif strcmp(str,′rv′)
y=@(x)alpha*x./[1+(alpha-1)*x];
f=@(T)xF*exp[CA(1,1)-CA(1,2)/(CA(1,3)+T)]-y(xF)*P;
tb=fzero(f,373)-273.15;
xx0=[xF,373];
r=fsolve(@Tdx_rv,xx0);
td=r(2)-273.15;
end
end
2.4 饱和气液相组成的计算
编辑一个名为sxy 的函数,用给定的方法和参数计算饱和气液相组成。
function [ x,y ] = sxy(TF,xF,alpha,str)
%sxy可以用直接计算法或相对挥发度法计算给定温度下的饱和液、气相组成x、y
% TF(K)为给定温度,xF为给定组成,alpha为某一种相对挥发度,str为方法字符串
global CA P
if strcmp(str,′dc′)%直接计算法
Psf=exp(CA(:,1)-CA(:,2)./(CA(:,3)+TF));%计算出给定温度下轻重两组分的饱和蒸气压列向量Psf(mmHg)
fun=@(x)Psf(1)*x+Psf(2)*(1-x)-P;
x=fzero(fun,xF);%求给定温度下的饱和液相组成x
y=x*Psf(1)/P;%求给定温度下的饱和气相组成y elseif strcmp(str,′rv′)
y=@(x)alpha*x./(1+(alpha-1)*x);
f=@(x)x*exp(CA(1,1)-CA(1,2)/(CA(1,3)+TF))-y(x)*P;
x=fzero(f,xF);
y=y(x);
end
end
2.5 主程序
新建一个名为tbtdxeye 的脚本文件,编辑代码如下:
clc,clear
global CA P xF xD xW alpha
%将Antoine 参数矩阵CA、总压P(mmHg)、进料液组成xF、塔顶产品组成xD 和塔釜产品组成xW、所选相对挥发度alpha定义为全局变量
CA=[15.9008 2788.51-52.36;16.0137 3096.52-53.67];
%定义Antoine 参数矩阵CA:第一行元素依次为苯的Antoine 参数A,B,C;第二行元素依次为甲苯的Antoine参数A,B,C
P=760;%给定气相总压(mmHg)
p=input(′请输入原料液和塔顶产品摩尔流量(kmol/h)、原料液和塔顶组成:′);%本例输入[10 5 0.5 0.95]
xF=p(3);xD=p(4);
xW=(p(1)*xF-p(2)*xD)/(p(1)- p(2));%根据物料衡算式求塔釜产品组成xW
%以下数步用以计算xLD
xt0=[xD 81+273.15];%定义初值向量xt0
xt=fsolve(@IDVLEpy,xt0);%调用fsolve 函数求解IDVLEpy定义的方程组
xLD=xt(1);xLD=[xLD;1-xLD];
%以下数步用以计算yW
yt0=[xW 110+273.15];%给出解IDVLEpx函数的初始值向量yt0
yt=fsolve(@IDVLEpx,yt0);%调用fsolve函数解IDVLEpx定义的方程组
yW=yt(1);yW=[yW;1-yW];
str={′geo′,′log′,′ari′};
a=zeros(size(str));
for i=1∶length(str)
a(i)=rvmean(xD,xW,xLD,yW,str{i});
end
tb= zeros(4,1);td=tb;
[tb(1),td(1)]= BDPT_2M(xF,a(1),′dc′);
for i=1∶length(a)
alpha=a(i);
[tb(i+1),td(i+1)]= BDPT_2M(xF,alpha,′rv′);
end
tF=input(′请输入进料温度(介于泡露点之间):(℃)′);
TF=tF+273.15;%进料温度单位换算(K)
x= zeros(4,1);y=x;
[ x(1),y(1)] = sxy(TF,xF,a(1),′dc′);
for i=1∶length(a)
alpha=a(i);
[x(i+1),y(i+1)]= sxy(TF,xF,alpha,′rv′);
end
3 结果与讨论
运行tbtdxeye脚本,命令窗口显示:
请输入原料液和塔顶产品摩尔流量(kmol/h)、原料液和塔顶组成:
输入[10 5 0.5 0.95 ]并回车,命令窗口显示:
请输入进料温度(介于泡露点之间):(℃)
输入95 并回车,计算完成后,在Workspace 中出现全部计算数据。
从Workspace 中复制相关计算结果,可得表2。从表2 可以看出,当以直接计算法为基准时,几何平均法计算的tb、td、xe和ye整体偏差最小(相对偏差依次为0.10%、0.34%、0.03%和0.03%);对数平均法的整体偏差也较小(相对偏差依次为0.10%、0.35%、0.06%和0.06%);算术平均法的偏差整体相对较大(相对偏差依次为0.09%、0.36%、0.12%和0.12%)。
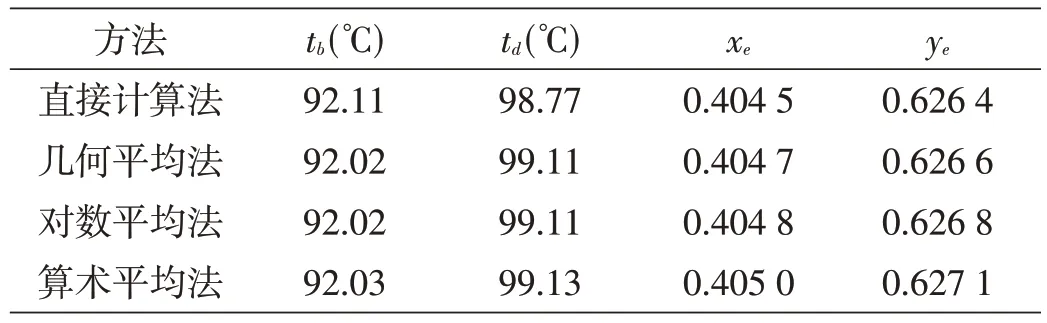
表2 四种计算方法的计算结果
由此可见,与直接计算法结果相比,几何平均法的整体计算效果相对最好,对数平均法次之,算术平均法最差;无论相对挥发度采用哪一种方法计算,三种相对挥发度法的各个计算结果的相对偏差均在0.2%以内,因此三种方法均可用于二元完全理想系相平衡关系的计算。
4 结论
本文创建了八个函数用于计算气液相平衡关系:IDVLEpy、IDVLEpx、rvmean、BPT、DPT、Tdx_rv、BDPT_2M、sxy。其中,IDVLEpy、IDVLEpx、BPT、DPT、Tdx_rv返回的均是需要求解的方程或方程组:IDVLEpy、IDVLEpx专用于以直接计算法计算塔顶和塔底再沸器的饱和液相或气相组成及其操作温度,而BPT、DPT、Tdx_rv 均为BDPT_2M 返回待求解方程组;rvmean 函数可根据给定的方法计算三种相对挥发度;BDPT_2M、sxy 可以两类方法(共四种方法)分别计算给定组成的泡露点温度、给定温度下的饱和气液相组成。以苯-甲苯体系为例,通过主程序tbtdxeye 调用相关函数可实现以四种方法计算泡露点温度及饱和气液相组成。通过相对偏差分析发现,以直接计算法为基准,三种相对挥发度法的整体精度顺序为:几何平均法>对数平均法>算术平均法。三种方法均可计算二元完全理想系相平衡关系,可进一步用于后续的精馏计算中。

