地理空间数据坐标转换研究与应用
张蒙,徐益峰
(苏州市测绘院有限责任公司,江苏 苏州 215000)
0 引 言
近年来,随着苏州市城市建设高速发展和市域一体化基础设施等互联互通,地理空间数据跨区域应用日趋频繁。然而,由于苏州市及下辖区(市)各自建立了相对独立的城市平面坐标系,各坐标系使用范围均不相同和未能够建立有效联系,导致了地理空间数据的坐标基准不一致,对其应用、共享和交换带来不便。2020年8月1日,苏州全市统一的苏州2000坐标系[1](CGCS2000椭球)正式启用(过渡期两年),解决了多套坐标系并存共用的问题。在此背景下,苏州市存量地理空间数据亟须完成向苏州2000坐标系的转换。
目前,诸如Coord等商用坐标转换软件定制化程度低;ArcGIS等应用平台虽然提供了相应的转换功能,但需要以明文的方式暴露转换参数,不利于参数保密[2-4];基于语义转换的FME虽然能够实现对地理空间数据的转换,但脱离了数据原生环境,亦存在转换参数保密等问题[5,6]。另一方面,除了对坐标的空间位置进行转换,还需考虑属性信息中的坐标值,如dwg实体的xdata、gdb要素类的属性字段。
因此,本文首先根据地理空间数据的常用类型和其应用平台确定了坐标转换时采用的转换模型。在分析苏州市已有坐标基准后,研究了苏州市原城市平面坐标系和CGCS2000(及苏州2000坐标系)建立联系的过程,并充分利用多平台开发组件库,研制了坐标转换平台,对转换模型和参数进行应用,实现了多类型数据的坐标转换。
1 坐标转换方法
1.1 转换模型
常用的坐标转换模型除了高斯投影坐标计算,还包括平面坐标转换模型和空间大地坐标转换模型两类[7]。其中的平面坐标转换模型包括三维四参数转换模型、二维四参数转换模型、多项式拟合(仿射变换)模型、格网内插(改正)模型等;空间大地坐标转换模型包括布尔沙七参数模型、三维七参数坐标转换模型、二维七参数转换模型等。
(1)高斯投影坐标计算,适用于同一地球椭球下不同中央子午线的平面坐标转换。部分坐标还需根据坐标系定义的X、Y方向加常数,在转换前后进行归算。
(2)平面坐标转换模型,一般适用于不同地球椭球框架下平面坐标转换。采用该模型时,需将坐标统一到同一中央子午线和投影高程面下,以消除投影变形不一致的影响;同一地球椭球框架下的不同平面坐标系,由于起算坐标不同等因素导致同名点存在坐标不一致的情况,在进行坐标转换时也可通过该模型完成。
(3)空间大地坐标转换模型,适用于不同大地坐标系的坐标转换。在进行平面坐标系坐标转换时,通过该模型建立空间直角坐标系之间转换关系后换算到大地坐标,再依据高斯投影坐标计算实现大地坐标与平面坐标的换算。
1.2 模型选取
常用的地理空间数据包括了文本型、矢量型和栅格型三类,根据不同数据类型及使用平台选择相适应的转换模型。其中,文本型的点记录和AutoCAD矢量数据的坐标转换,可直接采用平面四参数转换模型;由于gdb格式等矢量和tiff格式等栅格数据的主流应用平台ArcGIS的低版本中缺少四参数转换模型的选择项,对于该类数据的坐标转换可采用布尔沙七参数模型。坐标转换模型选取,如表1所示。

表1 坐标转换模型选取
因此,考虑到基于主流应用平台的坐标转换功能研发,采用平面四参数转换模型和布尔沙七参数转换模型。
(1)平面四参数转换模型
平面四参数转换模型适用于同一平面的坐标转换,常用的2类转换模型如下:
(1)
式中:(x1,y1)、(x2,y2)分别为某点转换前(源坐标系)、后(目标坐标系)的同一平面下的平面坐标系坐标(m);(△x,△y)、m、α分别为坐标系转换的平移参数(m)、尺度参数(ppm)、旋转参数(rad)。根据式(1)可知,同名点不小于2个。
通过内符合精度、外符合精度对转换参数的精度进行评定[8,9]。其中,内符合精度,利用计算参与转换的控制点坐标残差计算点位中误差Mp评定,详见式(2);外符合精度,通过计算均匀选择不少于5个未参与计算的控制点作为外部检核点,计算其误差σ进行外部检核,详见式(3)。
(2)
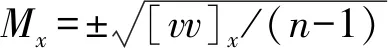
(3)
式中:m为检核点个数,△为检核点转换坐标值-已知坐标值。
不同中央子午线的平面坐标系间四参数计算流程如图1所示。

图1 计算四参数流程
同理,在计算目标坐标系坐标时,根据四参数所在平面的不同按图2的流程。

图2 根据四参数计算坐标流程
(2)布尔沙七参数转换模型
布尔沙七参数转换模型适用于不同地球椭球对应空间直角坐标系的坐标转换,常用转换模型如下:
(4)
式中:(X1,Y1,Z1)、(X2,Y2,Z2)分别为某点转换前、后对应的空间直角坐标(m),(△X,△Y,△Z)、m、(εX,εY,εZ)分别为坐标系转换的平移参数(m)、尺度参数(ppm)、旋转参数(rad,按顺时针定义)。根据式(4)可知,同名点不小于3个。该模型对应ArcGIS坐标变换方法COORDINATE_FRAME。
在求取七参数前,将平面坐标通过高斯投影坐标反算得到大地坐标(B,L)(令大地高H0=0.000 m)计算对应空间直角坐标后,利用式(4)的转换模型求取七参数。将转换成果计算到对应平面坐标后,按照式(2)、式(3)进行精度评定。
根据七参数转换模型,求取目标坐标系的平面坐标流程如图3所示。
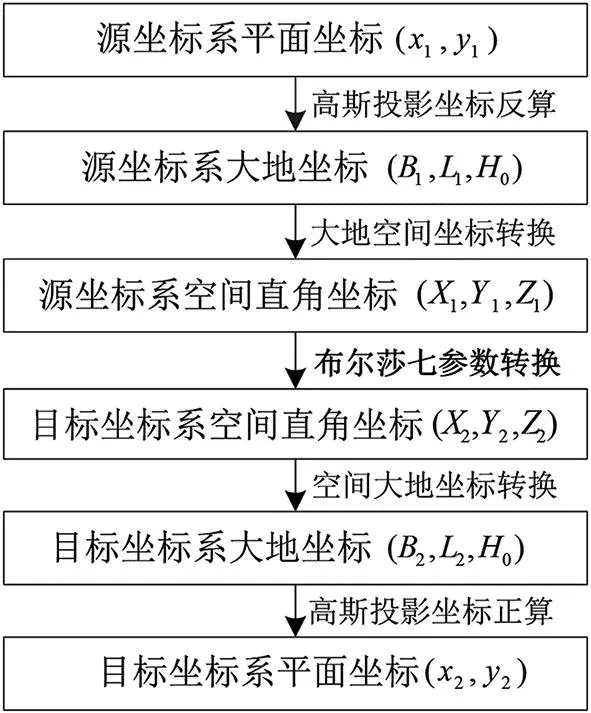
图3 根据七参数计算坐标流程
1.3 参数确定
(1)已有坐标基准情况
苏州市原城市平面坐标系包括了苏州独立坐标系等7套坐标,均建立在1954年北京坐标系框架下,坐标系投影面为克拉索夫斯基椭球面,各坐标系的主要使用范围均不一致,又由于受建设年代和起算数据的不同,导致同名点在1954年北京坐标系下坐标不一致。
其中的苏州独立坐标系(中央子午线为120°35′E)的主要应用范围包括了姑苏、相城、吴中、高新区、工业园区等5个区。根据式(5)计算并统计苏州独立坐标系下综合长度变形值δ0=△S0/S0,δ0<0.5 cm/km的区域占20.7%,超限区域占4.3%。
(5)
式中:Hm为归算边高出参考椭球面的平均高程(m),R为参考椭球面在地面边中点的平均曲率半径(km),ym为边长两端点的近似横坐标平均值(km)。
由图4中可知,从全市陆域范围来看其中央子午线略偏西,会引起东侧综合长度变形过大。因此,若以苏州独立坐标系为全市统一坐标系无法满足实际应用需要,CGCS2000椭球下的苏州2000坐标系建立成为必然选择。
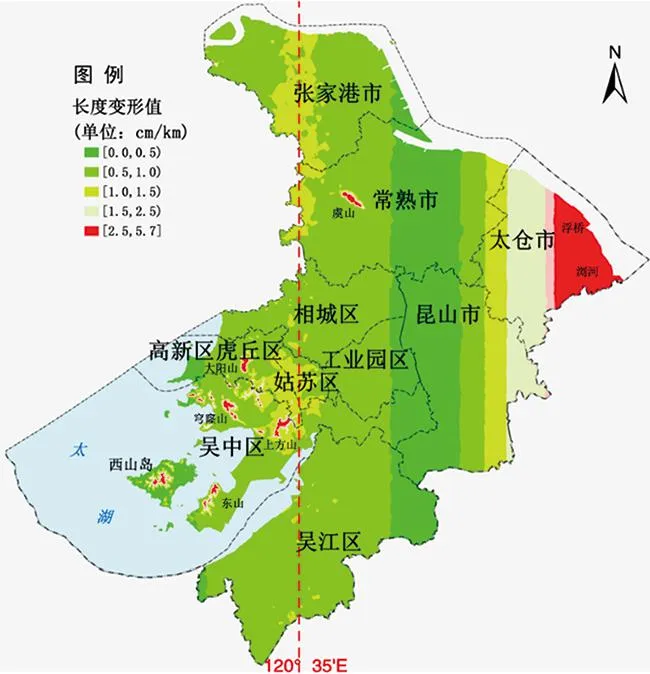
图4 苏州独立坐标系下综合长度变形分布
通过依次采用了平均高程法、格网占比法和离散点占比法的多方案分析、比选和可行性论证[1],最终的坐标系定义为:采用高斯投影,与CGCS2000椭球参数相同,中央子午线为120°47′E,投影面为CGCS2000采用的参考椭球面。
苏州2000坐标系下的综合长度变形统计及分布,详见文献[1]。通过与苏州独立坐标系结果对比分析可知:δ0<0.5 cm/km的区域占比提高了约50%,超限区域由4.3%降低到了0.7%,主要集中在低开发强度山区和东侧滩涂。由此可知,该坐标系定义方案是一种保重点大范围、兼顾边缘小区域的较优方案。
(2)参数计算
①建立CGCS2000空间框架
以苏州市空间定位信息服务系统(SZ-CORS)的基准站点作为苏州2000坐标系的基准点,组成基准框架网;通过与苏州及周边地区的JSCORS基准站联测,将CGCS2000坐标引入苏州;在此基础上,充分利用已有控制点,拓展覆盖苏州大市范围的B级GNSS控制网和加密覆盖各区(市)的C级GNSS控制网;最终形成“基准框架网-市级基本网-区市级加密网”的CGCS2000空间框架,如图5所示。

图5 苏州市CGCS2000空间框架
②转换参数确定
从原城市平面坐标系中各自择优选取5个以上的高精度控制点,在苏州市CGCS2000空间框架下完成联测和数据处理、平差计算,获取CGCS2000坐标成果,并根据苏州2000坐标系定义进行高斯投影正算,得到对应的苏州2000坐标系坐标成果;计算原城市平面坐标系与CGCS2000(及苏州2000坐标系)同名点的坐标转换参数。
以苏州独立坐标系与苏州2000坐标系相互转换为例,采用的基准站点为同名点,点位分布如图6所示。根据联测获取的CGCS2000(及苏州2000坐标系)坐标成果和收集的苏州独立坐标系坐标成果,按照式(1)、式(4)计算坐标转换的四参数(中央子午线120°35′E)和七参数。
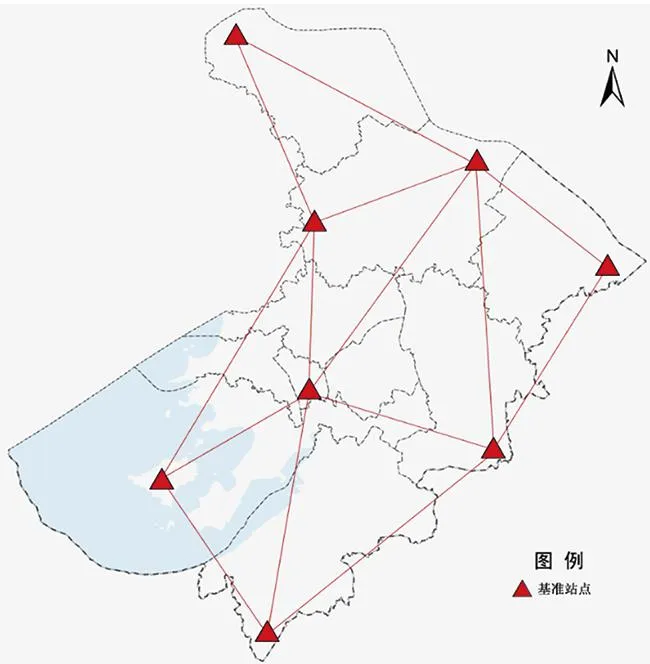
图6 同名点(基准站)点位分布示意
2 软件设计与转换实验
2.1 软件设计
(1)框架设计
框架设计时,将坐标转换平台划分为坐标转换、参数计算和平台管理等3个模块11类功能。功能划分如图7所示。
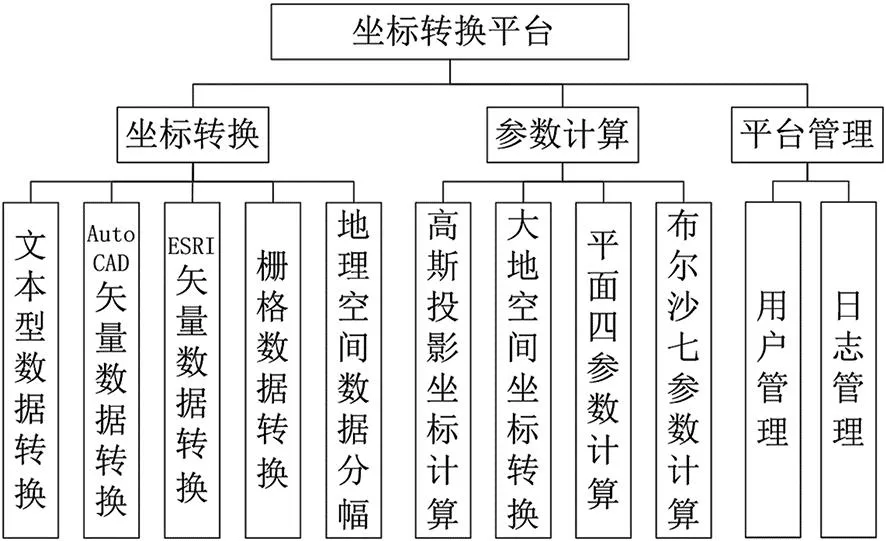
图7 功能结构
基于MFC和Ribbon UI组件库以扁平化用户界面进行表面集成,各模块采用COM接口后台调用相关组件库[10,11];针对不同类型的地理空间数据坐标转换,采用对应的开发语言及组件库进行控制集成实现功能,如针对dwg/dxf格式数据采用依赖于AutoCAD平台的C++、ObjectARX的方式。同时,根据客户机中依赖平台版本进行定制。
(2)多元化数据转换模式设计
为了保证同一转换模型的结果一致性,按照“高内聚、低耦合”的设计思路,对转换模型进行封装。以此为前提,按照数据类型采用不同的转换模式进行设计,具体如下:
①文本型点记录数据,直接坐标转换。
②AutoCAD矢量数据,采用逐个遍历图元转换更新位置信息,并根据配置文件同步更新Xdata中的坐标属性信息。已实现了(多)线段、块参照、标注等28种图元的转换[12]。
③ESRI矢量数据和栅格数据,采用ArcEngine组件库中的Project、ProjectEXd等接口整体坐标转换后,根据配置文件更新要素字段的坐标属性信息。
④针对分幅数据转换后重分幅效率低、内存占用率高的问题,应用了二维哈希算法和文件数据临时资源池[13]。
2.2 转换实验
(1)平台实现
采用上述框架和方法实现了对表1中数据的转换功能,完成了苏州市坐标转换平台的研发,并通过了国检中心、江苏省质检站的功能、精度和性能测试;在此基础框架上,根据各区(市)具体需求定制开发了区级坐标转换平台。同时,采用软件锁和研发授权管理平台,通过“一机一码、软硬结合”的方式进行了保密处理和授权管理。
(2)精度分析
通过“参数计算”功能完成CGCS2000(及苏州2000坐标系)和苏州独立坐标系坐标转换的四参数和七参数的内符合精度分析;另外,选取了市级基本网中均匀分布的10余个B级GNSS控制点为外部检核点(图8),通过“文本型数据转换”功能计算转换值后,按照式(3)分析外符合精度。统计如表2所示。
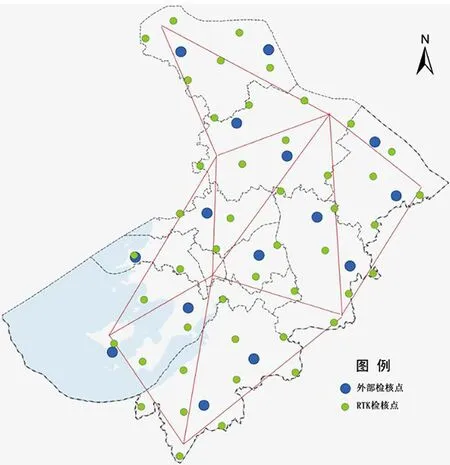
图8 检核点点位分布示意
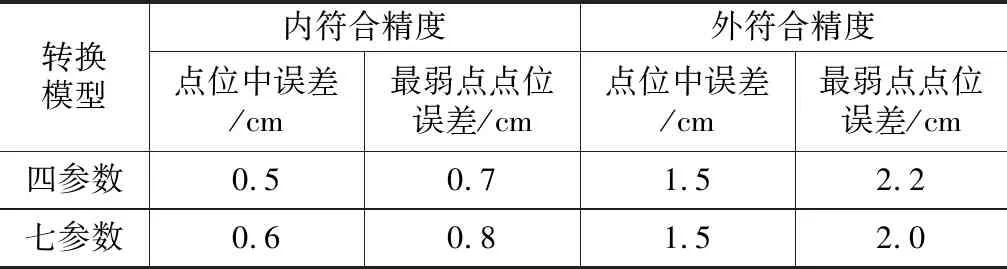
表2 转换模型参数误差统计
同时,在大市范围内提取均匀的40余个特征点(图8),采用二级GNSS控制测量的方式,通过SZ-CORS网络RTK实测苏州2000坐标系和苏州独立坐标系坐标。将苏州独立坐标系的实测值转换至苏州2000坐标系的转换值与实测值进行误差分析,统计如表3所示。

表3 转换误差统计
由表2、表3可知,转换参数误差、转换值与实测值误差均小于规范要求的 5.0 cm。由此可知,转换模型和参数可靠,可应用于实际数据转换中。
(3)可行性验证
通过内、外符合精度分析及特征点精度检核,构建的多元化坐标转换模型满足现有规范要求;经测试验证,研发软件具有良好的人际交互体验,已应用在苏州市本级和各区(市)的基础测绘、自然资源等相关存量地理空间数据的坐标转换工作,并为自然资源和规划、住建、水务等相关领域提供坐标转换平台和服务。经实际工程验证,满足现有数据共享应用及实际工程生产应用需求。
3 结 语
针对不同类型的地理空间数据及其应用平台,研究确定了按类型进行坐标转换的思路。以苏州独立坐标系为例,通过控制点的联测和转换参数的计算建立了与CGCS2000(及苏州2000坐标系)联系,并对转换参数进行精度评定,确定了转换模型的可靠性。结果表明四参数和七参数转换模型均能够满足坐标转换的精度要求。
基于二次开发组件库研制了坐标转换平台,通过了第三方测试,实现对主流数据类型的坐标转换和参数计算功能。通过对存量数据的转换,进一步验证了软件的适用性和转换模型的可靠性。

