基于SPH-DEM的泥石流冲击刚性防护结构的动力过程研究
赵德博,郝梦洁,熊 昊
(1. 深圳大学 土木与交通工程学院,广东 深圳 518060; 2. 深圳大学 滨海城市韧性基础设施教育部重点实验室,广东 深圳 518060)
0 引言
泥石流作为一种山区地带多发的地质灾害,包含泥砂、块石的固液两相流体,呈黏性层流或稀性紊流状态[1]。由于其往往突然暴发、来势凶猛、破坏力强,泥石流对人类的生命财产安全构成巨大威胁。我国泥石流几乎遍布每个省、市和自治区,据自然资源部统计,仅2022年上半年,特别是5月底以来,南方多省遭遇多轮强降雨,地质灾害多发群发,特别是浙江、福建、江西、湖南、广东、广西6省(区)发生4000多处崩塌滑坡泥石流,已超去年全年的数量[2]。2019年6月27日20时30分,四川省金川县曾达乡曾达沟(流域面积125.53 km2)暴发特大型泥石流灾害,造成房屋、基础设施、农业、公益设施损失约1.51亿元[3]。泥石流灾害后果极为严重,因此对于泥石流易发区域迫切需要采取治理措施。沿着泥石流路径建造防护结构是目前泥石流治理采用的主要工程措施。防护结构主要包括刚性[4]和柔性[5-6]2种,它的设计可以改变泥石流的运动状态,减弱甚至避免泥石流对下游造成破坏。然而目前在工程实践中,主要还是采用经验方法对防护结构进行设计与施工。究其原因,主要是缺乏对泥石流运动特点以及泥石流与防护结构相互作用机理的研究。
许多研究人员都通过现场实测、室内水槽试验和数值模拟[7-9]等手段对泥石流对防护结构的冲击开展过探究。刘道川等[10]通过小型水槽试验开展了系列泥石流的冲击试验研究了两相泥石流冲击力的时空分布特征。而NG等[11]将泥石流简化为均一的流体,借助水槽试验研究了玻璃球和砂子分别作用于刚性防护结构的冲击特性和机理,揭示了玻璃球作用下的爬升机制和砂颗粒作用下的堆积机制。此外,其他学者利用水槽试验装置研究了不同组成成分的泥石流与防护结构的作用机制,发现泥石流的堆积形态、爬升高度和泥石流的组成密切相关[12-13]。相比于原型场试验,小尺度水槽试验存在明显的尺寸效应,无法完全还原泥石流的动力学特征。但大尺度的原型试验成本较高,工作量大,不确定因素多,不适合泥石流对防护结构冲击机理的探究。因此,近年来数值模拟在岩土工程方面[13-15],尤其是泥石流运动机理方面得到广泛的应用[16]。甘建军等[8]采用RAMMAS3D数值软件准确模拟了泥石流的运动变形过程并确定了其影响区域。HE等[17]利用光滑粒子流体动力学(SPH)方法模拟了干颗粒流和刚性防护结构的作用,而CUI等[18]利用离散元法研究了不同粒径的颗粒流撞击防护系统的过程,并与试验结果进行比对,取得了较好的效果。CALVETTI等[19]则从微观角度解释了干颗粒流对防护结构的冲击。但以上数值模拟方法都倾向于将泥石流模拟为单一相的流体,这种简化限制了对泥石流这种多相流体的深入理解。
因此,本研究采用SPH-DEM耦合方法开展水槽试验的数值模拟,其中SPH模拟泥石流中的黏性流体,DEM模拟泥石流中的石块,探究含石块的泥石流的运动过程及其对刚性防护结构的冲击效应,并研究了不同水槽倾角对泥石流的运动形态以及对刚性防护结构的冲击力的影响,为刚性防护结构强度的工程设计标准提供参考。
1 SPH-DEM数值模拟方法
1.1 SPH数值方法
光滑粒子流体动力学(smooth particle hydrodynamics,SPH)是一种纯拉格朗日无网格粒子方法,是当前数值计算的热点话题之一。该方法基于连续介质假设以一系列任意分布的粒子来模拟流体运动规律,其中每一个粒子都有独立的影响域和插值域,计算过程中粒子的速度、压强和位置等性质以及它们的梯度分布都是根据插值域内粒子构造的核近似函数插值得到的。
在SPH方法中,位于r处的流体粒子特性的函数可由以下的积分表达式定义:
(1)
式中:h为光滑长度,控制积分域的大小;Ω为支持域;r′为支持域内其他粒子的位置;W为核函数,它不仅决定了SPH近似的内值精度,而且与数值稳定性有关。本文采用Wendland核函数[20]进行平滑,其表达式为:
(2)
式中:αD在二维问题中等于7/(4πh2),在三维问题中等于21/(16πh3);q=|r-r′|/h。
1.2 DEM数值方法
离散单元法(discrete element method,DEM)最早是由CUNDALL[21]于1971年提出的,已被广泛应用于颗粒材料[22]、岩土工程[23]等领域。DEM的基本思想是利用一系列离散的粒子来模拟固体介质,其中每个粒子作为一个单元,具有固定的大小和形状,单元之间可以在小范围内相互挤压重叠从而产生相互作用力。当单元i与单元j接触时,根据牛顿第二定律,单元i的运动方程可以写为:
(3)
(4)
式中:mi为流体粒子i的质量;u为单元i的运动速度;g为重力加速度;Fn,ij和Ft,ij分别是单元j对单元i的法向和切向作用力;Ii和ωi分别是单元i的转动惯量和角速度;而Tt,ij为Fn,ij和Ft,ij对单元i的力矩。
为了简化接触模型,单元均用球形粒子来表示,那么对于发生碰撞的球形粒子,粒子间的法向接触力如式(5)所示:
Fn=knδn+cnvn
(5)
式中:kn为法向刚度系数;δn为法向叠合量;cn为法向黏性阻尼系数;vn为法向相对速度。
粒子间的切向力大小与相接触的粒子间的相对速度有关,满足库仑定律,如式(6)所示:
Ft=min(ktvt,μFn)
(6)
式中:kt为切向刚度系数;vt为切向相对速度。
1.3 SPH-DEM耦合方法
SPH和DEM的耦合计算实际上是将流体作用于固体颗粒表面上的作用力进行积分得到流体对固体的作用力,而固体颗粒表面单元内插到与其相邻的流体粒子的SPH方程中,从而可以计算固体对流体的作用力。
在SPH-DEM耦合方法中,流体粒子的动量方程式为:
(7)
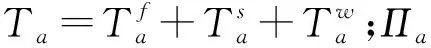
固体DEM颗粒所受的作用力主要包括固体颗粒间的接触力、润滑力、流体施加的力(浮力和阻力)和重力等,其控制方程式为:
(8)
(9)
2 SPH-DEM方法验证
为了验证本文采用的SPH-DEM耦合方法在模拟流体与固体之间复杂相互作用的可靠性,模拟了单个非旋转球体的入水测试,并结合ARISTOFF等[24]开展的室内试验和XU等[25]进行的模拟校验结果。
试验模型的装置如图1所示,水箱的长为0.20 m,宽为0.20 m,高为0.14 m,水深0.11 m。直径为25.4 mm的球体以2.17 m/s的初始速度与水面相切释放。数值模拟中使用的球体和水的参数如表1所示。模拟时考虑重力,重力加速度为9.81 m/s2。SPH流体粒子初始间距dp为球体半径的1/10,采用Verlet时间积分算法,模拟1 s内小球进入水中的运动状态。
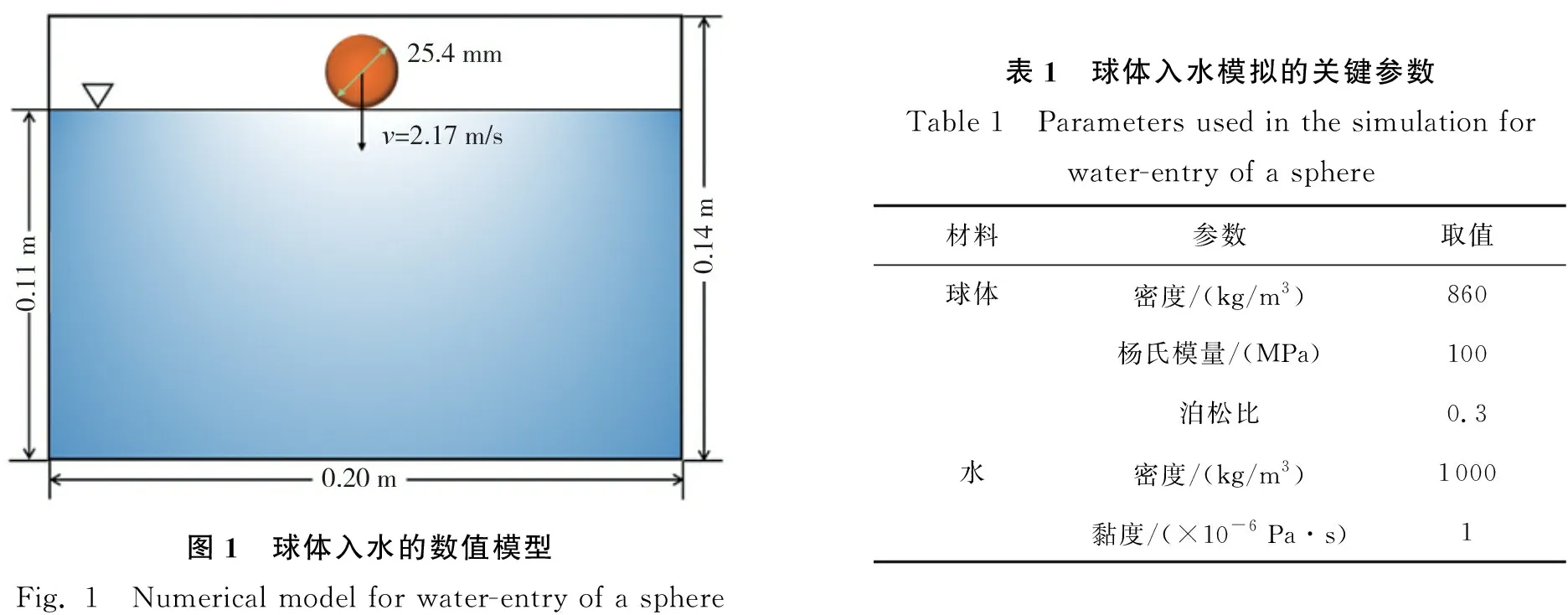
图1 球体入水的数值模型Fig. 1 Numerical model for water-entry of a sphere表1 球体入水模拟的关键参数Table 1 Parameters used in the simulation for water-entry of a sphere材料参数取值球体密度/(kg/m3)860杨氏模量/(MPa)100泊松比0.3水密度/(kg/m3)1000黏度/(×10-6 Pa∙s)1
不同时刻小球进入水中的运动过程如图2所示,与ARISTOFF等[24]的试验在下降趋势、水面形状等方面一致。球体与水面接触并开始向下运动,冲击并挤压水,致使球体周围的水流向侧向运动,并在球体上方形成一个空腔。随着小球继续向下运动,空腔塌陷,形成向上的水射流。而球体由于密度较小,速度逐渐减小为0,随后在浮力的作用下被抬升。球体的整个运动轨迹都是沿一条垂直直线,没有任何的旋转。这是因为球体在耦合过程中只受来自垂直方向的力,这与理论情况也是相符的。

图2 小球入水过程模拟图Fig. 2 Simulation snapshots of the sphere entering water
球体入水深度随时间的变化情况如图3所示,并与试验数据、理论数据和XU等[25]的模拟结果做了对比,发现在0.07 s之前,随着时间的不断增大,球体在水中的深度逐渐变大,但深度的增大率,即球体的速度却逐渐变小。模拟效果与理论结果较为接近,且由于所采用的粒子间距大于XU等[25]的模拟但结果相差不大,模拟效率大大提升。由此可见,本文采用的SPH-DEM耦合方法具有可行性,能够较好地模拟流体与固体之间的相互作用。

图3 球体入水的深度随时间的演变Fig. 3 Evolution of the depth of sphere into the water with time
考虑到多数泥石流中的流体均为黏性流体,本文进一步研究了球体进入黏性流体的运动,并提取其深度,如图4所示。可以看到在黏性流体(黏度=1)中,球体的深度随时间变化得慢,速度减小得快,在0.8 s左右,速度基本为0。因此,耦合模型模拟黏性流体与固体的相互作用依旧有效且可靠。
3 泥石流冲击刚性防护结构
长期以来,泥石流频发区防护结构的设计一直是人们关注的问题。目前许多学者已经针对泥石流与防护结构的作用过程开展了大量试验研究。其中CHOI等[26]利用小型水槽装置研究了不同倾角下干性泥石流冲击下,防护结构的动态受荷过程,揭示了水槽倾角与冲击力对防护结构设计的重要性。本文采用SPH-DEM的耦合方法模拟水槽试验中包含石块的泥石流在水槽内的流动以及对刚性防护结构的冲击,在此基础上改变水槽倾角、石块的粒径、泥石流中流体的体积,从而分析了不同条件下防护结构所受冲击力以及其上水面高程的演变。
3.1 计算模型
水槽试验模拟的数值模型尺寸如图5所示。水槽的长、宽和高分别为2.3、0.6、0.7 m,防护结构距离料箱门1.6 m,料箱的容量为0.168 m3。防护结构的宽度、高度和厚度分别为600、700、5 mm。水槽底部与水平面的倾角为15°。

图5 水槽试验模拟的模型示意图Fig. 5 Schematic diagram of the model for the simulation of the flume experiments表2 水槽试验模拟的关键参数Table 2 Parameters used in the simulation of the flume experiment材料参数取值流体密度/(kg/m3)1000黏度/(Pa·s)1玻璃珠密度/(kg/m3)2000杨氏模量/MPa200泊松比0.2动态摩擦系数0.2恢复系数0.6
在初始状态时,泥石流位于水槽顶部,由固液两相组成。其中由SPH模拟泥石流中的黏性流体,流体的体积为0.072 m3,流体的黏度为1 Pa·s,流体粒子之间的间距为0.005 m,流体总粒子数为573934,而采用直径为4 cm 的玻璃珠模拟泥石流中的石块,本模拟中包含27个玻璃珠,即模拟的泥石流的固体体积分数为1.26%。整个模拟过程中考虑重力,重力加速度被设置为9.81 m/s2。模拟需要用到的其它参数如表2所示。
3.2 泥石流运动过程分析
泥石流在水槽中运动过程的模拟图如图6所示,SPH粒子的颜色代表流体的流速。在模拟之初,泥石流被生成在水槽顶部的料箱中,料箱门可以有效地阻止泥石流的运动。当料箱中的泥石流达到稳定状态(T=1.5 s)后,料箱门向上抽出,模拟泥石流的启动。在重力的作用下,两相流沿着水槽底部运动。随着运动速度的不断增大,泥石流中的流体前部逐渐靠近刚性防护结构,当其一接触到防护结构,流体的速度迅速减小,并沿着防护结构向上爬升(T=2.5 s),在其动能减少为0后,流体达到最大爬升高度,开始向后回滚(T=2.8 s),一部分堆积在防护结构的底部,形成一个稳定的堆积区,一部分与后续泥石流相撞,使其速度减少(T=3.1 s),而后续的泥石流不会直接撞击到防护结构,而是直接汇入堆积体,堆积区的大小逐渐增大,直至达到稳定,而泥石流中的玻璃珠由于与水槽底部的摩擦以及与流体的相互作用的影响,运动速度要小于流体,故其到达防护结构的时间更晚,在流体已经形成堆积体时,玻璃珠会沿着堆积体向上运动(T=5.0 s)。

图6 泥石流的运动过程Fig. 6 Runout process of the debris flow
为了进一步量化分析泥石流对防护结构的冲击效应,模拟中还提取了泥石流中的黏性流体对防护结构的冲击力随时间的演变,如图8中的绿色曲线所示。在t=2.36 s时,流体前端接触到刚性防护结构底部,动态冲击力由0迅速增大,流体沿着防护结构向上爬升时,冲击力增加速度放缓,随后随着流体爬升到最大高度后开始回流以及后续泥石流的冲击,冲击力存在波动并在2.8 s左右达到峰值。之后的泥石流由于被堆积在防护结构后部的流体阻挡,并不能直接接触到防护结构,故对防护结构的冲击力逐渐减弱并趋于平缓,造成这种现象的原因主要是泥石流体积是一定的,防护结构后的冲击力流量不再随着时间继续增加。而稳定前曲线仍存在的微小波动,是由于防护结构后堆积体的回流以及后续流体汇入堆积体对防护结构存在挤压间接造成的。
泥石流与防护结构的相互作用受多种因素的共同影响,包括泥石流的属性(如泥石流的体积、固体体积分数、密度和流体黏度等)、防护结构的位置、坡度以及水槽倾角等,这些都是设计防护结构需要考虑的重要因素。因此,本研究基于以上水槽试验模型进行多次模拟,探究不同影响因素下泥石流对防护结构的冲击效应。
3.3 水槽倾角的影响
为了比较不同水槽倾角对泥石流与防护结构相互作用的影响,分别设置θ=0°、8°、15°、24°、30°进行模拟。图7为在模拟最终时刻t=6.0 s时,不同水槽倾角下泥石流的最终形态,对比发现水槽倾角越大,泥石流形成的堆积区体积就越大(θ=30°时除外),且只有θ=30°时,泥石流撞击防护结构发生了溢流。这是因为水槽倾角越大,泥石流的动能越大,前端接触到防护结构的泥石流越不易发生回流。同时,可以观察到倾角越大,悬浮在流体上的玻璃珠数量越少,这是因为流体对颗粒向上的浮力减小导致的。
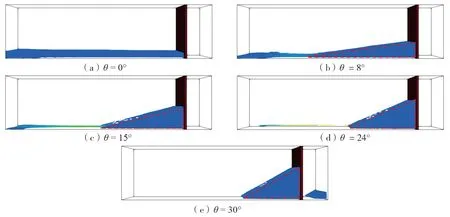
图7 不同水槽倾角下泥石流的最终形态Fig. 7 Final shape of debris flow at different inclinations of the flume
通过比较不同水槽倾角下,泥石流对防护结构的冲击力随时间的变化情况,进一步分析了水平倾角对于泥石流对防护结构的冲击效应的影响,如图8所示。显然,冲击力的变化趋势基本相似,先迅速增加,达到峰值冲击力后再慢慢下降,并逐渐趋于稳定。但θ>15°时,冲击力曲线会出现2个明显的波峰,且后者为峰值冲击力,这种现象的发生是因为第一个波峰主要是由流体前部对防护结构的撞击导致,随着流体的回流冲击力减弱,后部流体的动能仍较大,超过前部流体对其的阻碍,故出现了第二个波峰。而θ<15°时,后部流体的动能小于前部流体回流的阻碍,所以只存在一个波峰。同时,注意到若以θ=0°时的峰值冲击力50.26 N为基准,则θ=8°时峰值冲击力为其的2.59倍,随着倾角的增大,其倍数依次为4.75、8.88和11.45,倾角越大其峰值冲击力的增长率越大。且通过图像可以看出,在趋于稳定前,倾角越大,冲击力波动越大,这是因为流体的反复冲击与回流。稳定后的冲击力差异也很大,这是由于防护结构底部堆积体的体积不一致导致的。提取防护结构中心轴处水面高程随时间的变化情况如图9所示。由图9可知,倾角越大,到达防护结构的时间越短,并且沿防护结构爬升的高度越大,最后稳定时的水面高程也越大,但稳定后水面高程的增加率是随倾角的增大而逐渐减小的。同时水面高程达到稳定的时间随倾角的增大而变长,即泥石流与防护结构的动态作用时间随倾角的增大而增大。
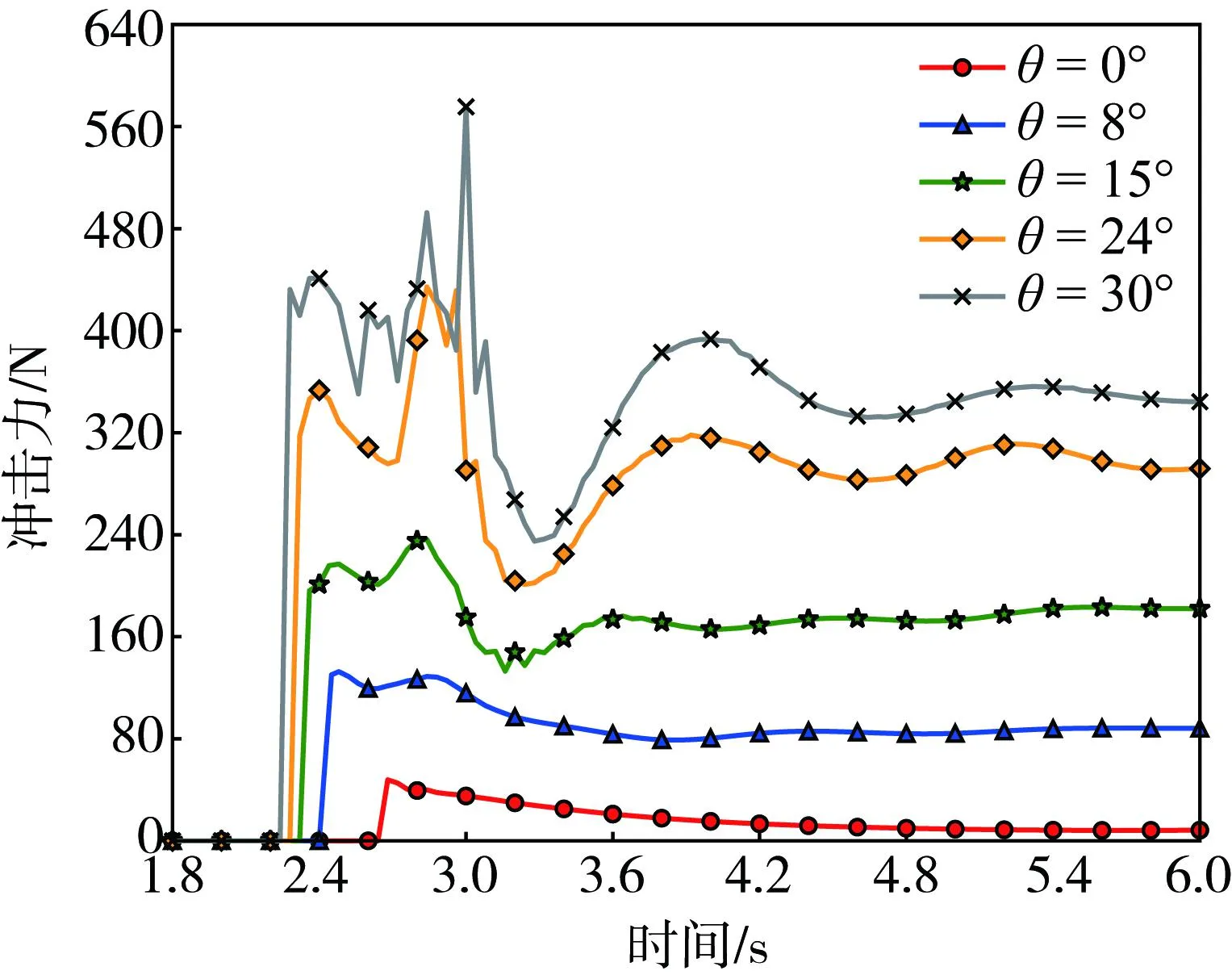
图8 不同水槽倾角下冲击力随时间的变化Fig. 8 Relationship of impact force-time at different inclinations of the flume
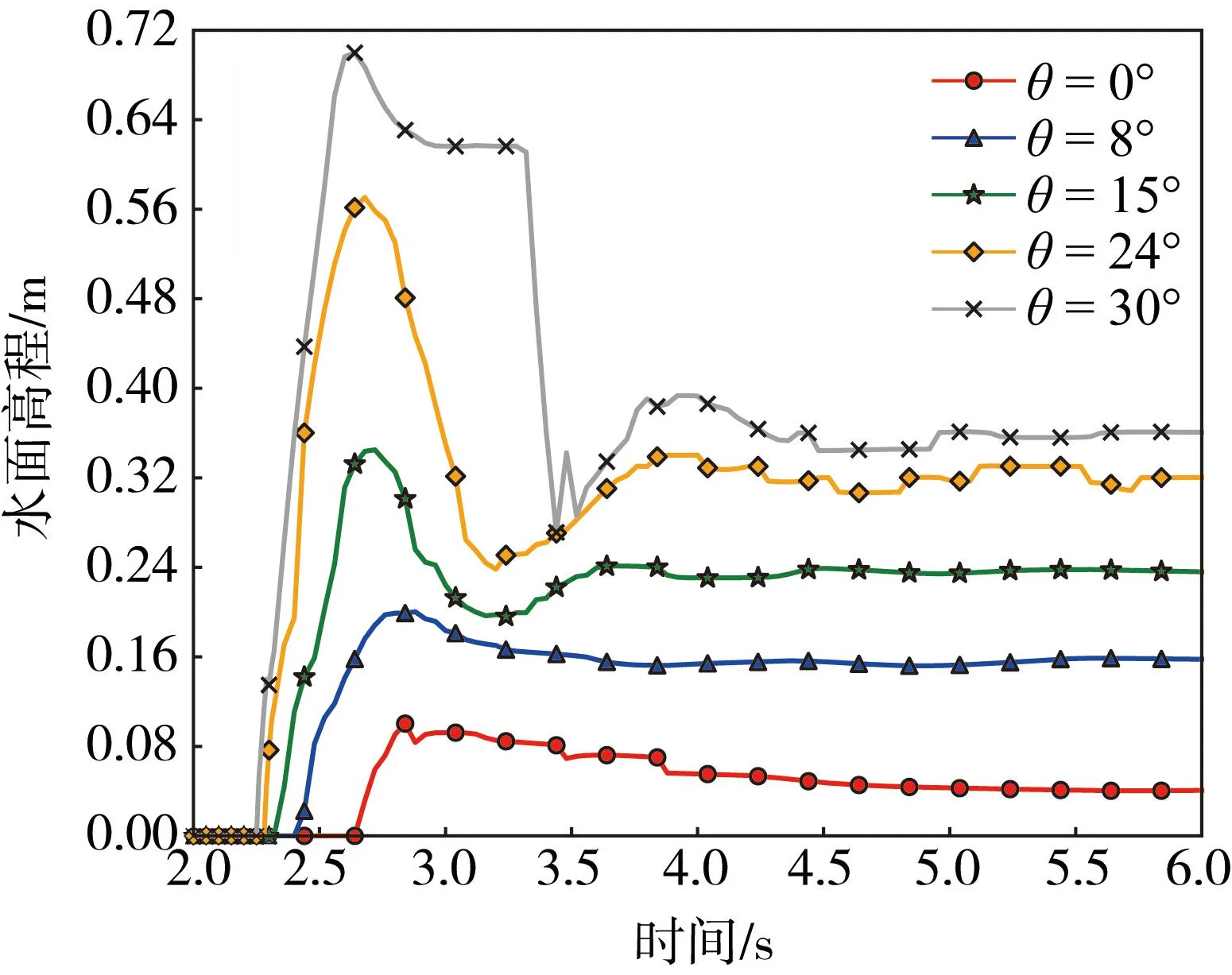
图9 不同水槽倾角下水面高程随时间的变化Fig. 9 Relationship of water surface elevation-time at different inclinations of the flume
综上所述,改变水槽倾角对于泥石流对防护结构的冲击效应的影响是显著的,不仅冲击力会成倍地变化,当防护结构的高度低于泥石流沿防护结构爬升的高度时,还会有溢流现象发生。因此在工程实践中,设计防护结构前考虑泥石流易发处的地形倾角,模拟泥石流对防护结构的冲击特性是非常必要的。
3.4 泥石流体积的影响
在自然灾害中,泥石流的暴发规模不同,其造成的危害程度是不一致的,那么需要采取的预防措施便也不同。本文为了探究不同规模泥石流对防护结构冲击的影响,将泥石流中流体部分的体积V分别设置为0.024、0.048、0.072、0.096、0.120 m3进行模拟。图10比较t=6.0 s时刻不同流体体积的泥石流运动形态,可见流体体积的增多导致固体体积分数的减小,会促进流体与颗粒间的相互作用,从而一定程度上增加玻璃珠的动能。图11进一步比较不同流体体积下冲击力随时间的变化,可以看出,流体体积越大其接触到防护结构所需的时间会越短,达到稳定冲击力的时间越长。同时,流体规模越大,其对防护结构的峰值冲击力和静态冲击力都越大。随着流体体积的增大,其峰值冲击力增长率也逐渐变大,相较V=0.024 m3分别增长了0.79倍、1.64倍、3.20倍和4.56倍,但是稳定下来的静态冲击力基本与体积的变化成正比。结合图12水面高程随时间的变化可以看到,虽然水面高程随流体体积的增大而增高,但流体达到最大水面高程所需时间基本相同。而且最大水面高程的增长率随体积的增大表现为先增加后减小的趋势,分别为27%、47%、33%和21%;稳定后水面高程的增长率随体积的增大则依次递减的,分别为76%、21%、15%和13%。也就是说,在实际工程中为能更加经济环保地设计防护结构,可以考虑在保持一定高度时,适当增强防护结构的强度以阻挡较大规模的泥石流。
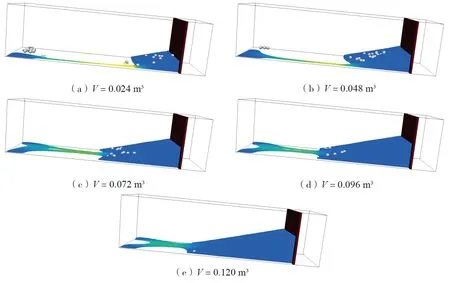
图10 不同流体体积下泥石流的最终形态Fig. 10 Final morphology of debris flow with different fluid volumes

图11 不同流体体积下冲击力随时间的变化Fig. 11 Relationship of impact force-time with different fluid volumes
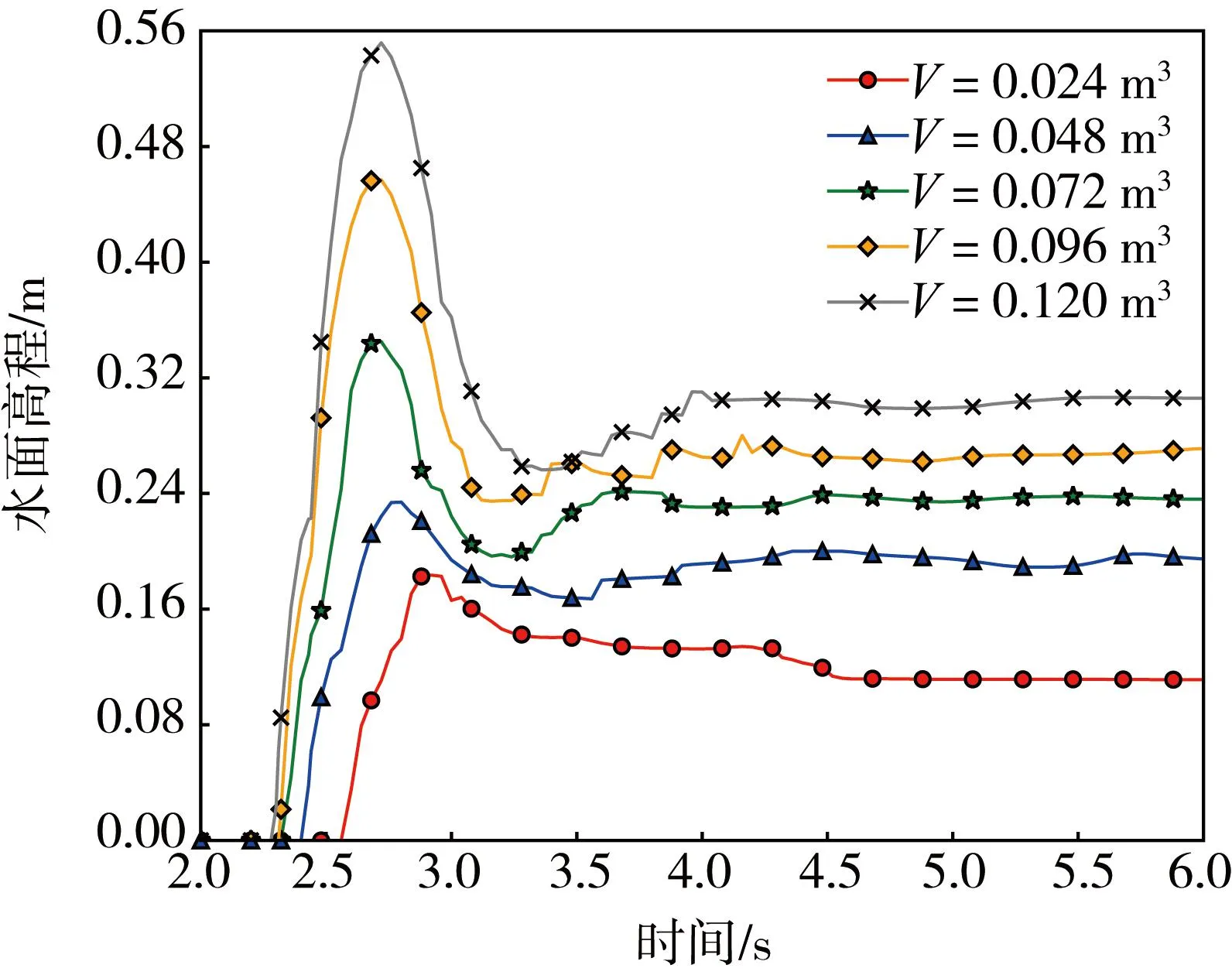
图12 不同流体体积下水面高程随时间的变化Fig. 12 Relationship of water surface elevation-time with different fluid volumes
3.5 石块粒径的影响
此外,本研究还考虑了其他条件一定的情况下,泥石流中石块粒径的改变对泥石流与防护结构相互作用的影响。在确保石块总体积不变时,模拟球形石块半径R分别为10、20、30 mm时,泥石流对防护结构的冲击。由图13中t=6.0 s时刻不同石块粒径下泥石流的运动形态可以看出,相同体积下,石块粒径越小,其与流体的接触面积越大,对流体的拖曳力的反作用力越强,则越易阻碍流体的运动。而图14展现的防护结构所受冲击力的变化则表明,由于固体体积分数较小,石块粒径的改变对峰值冲击力的影响不大,但是石块粒径越大,泥石流对防护结构的静态冲击力越易波动,这可能是由于大块石对流体回流的阻碍更弱导致的。同时,由图15可知,石块粒径越大,流体的最大水面高程越大,但石块粒径对稳定后的水面高程基本没有影响。因此,对于含有大块石的泥石流,在设计防护结构时可以适当提高防护结构的高度来对泥石流起到更好的阻挡效果。
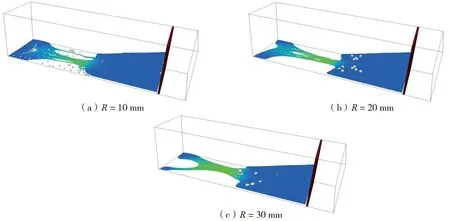
图13 不同石块粒径下泥石流的最终形态Fig. 13 Final morphology of the debris flow with different rock radii
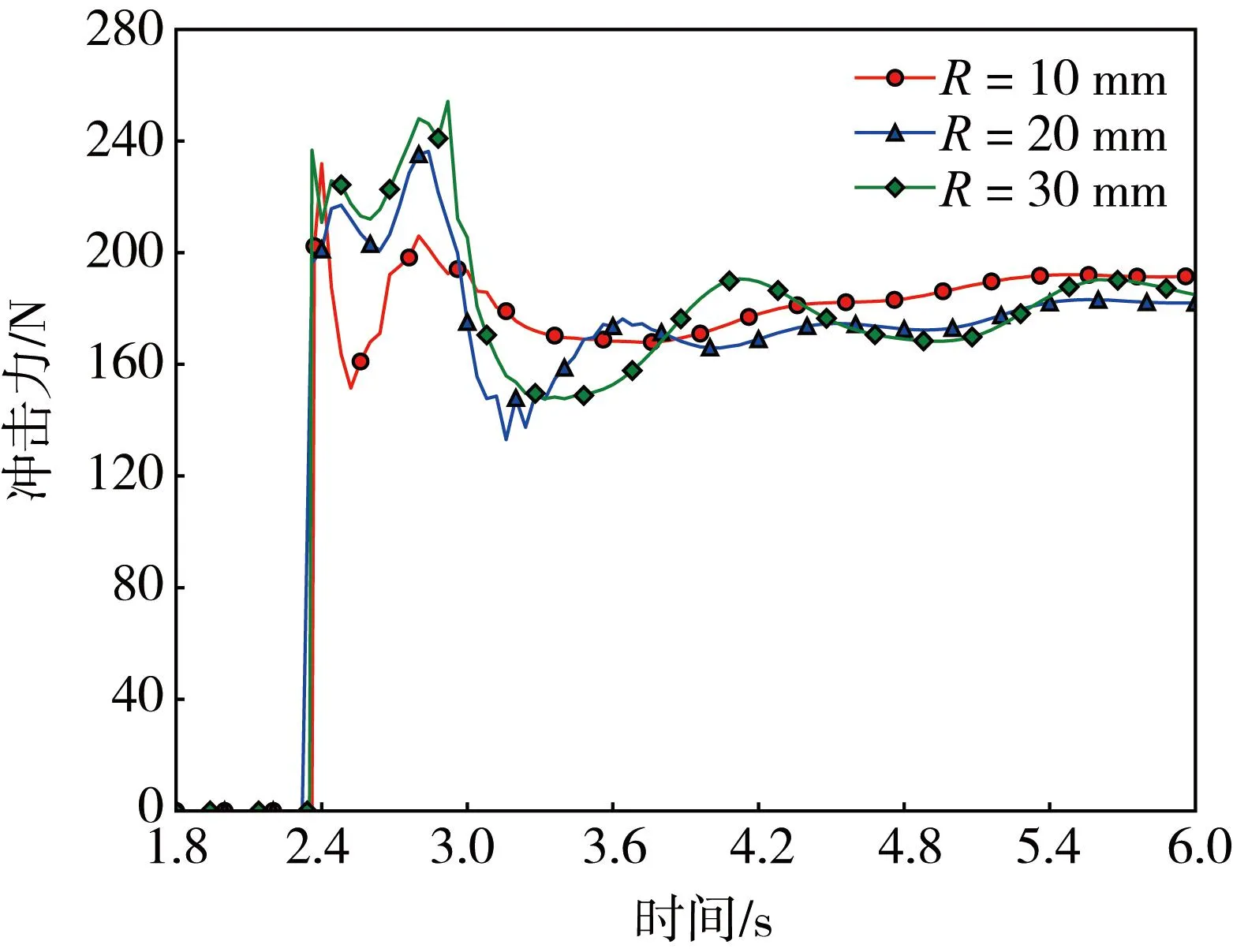
图14 不同石块粒径下冲击力随时间的变化Fig. 14 Relationship of impact force-time with different rock radii
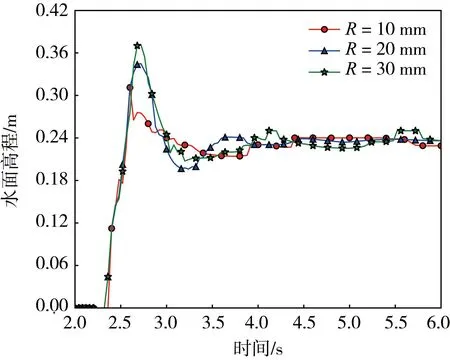
图15 不同石块粒径下水面高程随时间的变化Fig. 15 Relationship of water surface elevation-time with different rock radii
4 结论
本文利用球体入水试验验证了SPH-DEM耦合方法在模拟流固两相相互作用时的可靠性。基于验证方法进一步建立了水槽试验中含石块的泥石流冲击刚性防护结构的模型,并研究了泥石流的运动过程及对刚性防护结构的冲击效应,分析了不同水槽倾角、不同泥石流流体体积和不同石块粒径的情况下冲击力和水面高程的变化,得出以下结论:
1)通过与试验、理论结果的对比分析表明,采用耦合的SPH-DEM方法可以较好地模拟固液两相的相互作用,其中SPH模拟流体,而DEM模拟固体。而且该方法对模拟含石块泥石流的运动过程依旧可靠。
2)含石块泥石流与防护结构的相互作用可以分为3个阶段:冲击、爬升和堆积。当水槽倾角较大时,也可能会有溢流发生。泥石流中的黏性流体对防护结构的冲击力先迅速上升达到峰值冲击力后逐渐下降并趋于稳定,稳定后的冲击力不为0。而其中的石块由于与流体的相互作用以及水槽底部的摩擦的影响,运动速度小于流体且会沿着堆积体向上攀爬。
3)水槽倾角、流体体积和石块粒径对于泥石流与防护结构的相互作用影响显著。随着倾角由0°依次增长为8°、15°、24°和30°,峰值冲击力增长倍数依次为2.59、4.75、8.88和11.45,倾角越大其峰值冲击力的增长率越大。但稳定后水面高程的增加率是随倾角的增大而逐渐减小的;随着流体体积的增大,其峰值冲击力增长率也逐渐变大,相较V=0.024 m3分别增长了0.79倍、1.64倍、3.20倍和4.56倍,但是稳定下来的静态冲击力基本与体积的增长成正比;石块粒径的改变对冲击力的影响不大,但会影响峰值水面高程的形成,即石块粒径越大,峰值水面高程越高。

