基于一种距离相关的超高维生存数据Model-Free特征筛选

潘莹丽, 王昊宇, 喻佳丽, 刘展

(应用数学湖北省重点实验室, 湖北大学数学与统计学学院, 湖北 武汉 430062)

0 引言

随着时代的进步,科学技术快速发展,高维数据乃至超高维数据频繁出现在科学研究的各个领域。超高维数据的特征是变量维度p随样本量n呈指数阶增长,满足p=O(nα),α>0,其携带的信息量一方面让我们更加全面、客观、深入地了解研究对象,一方面又大大增加了数据分析的难度。模型中如果涉及的变量过多,不仅会增大模型的预测误差,还会使模型的算法变得冗余和复杂,从而导致计算时间长、运行速度慢、算法稳定性差等一系列问题,所以建模前对要纳入模型的变量进行选择十分必要。对于协变量维度略高于样本量的高维数据,传统的正则化变量选择方法,如LASSO、SCAD、自适应LASSO和MCP在实际运用中能准确选出对响应变量存在显著影响的重要变量。但超高维数据复杂程度高,上述正则化方法在处理这类数据时运算速度、统计准确性及算法稳定性均受到极大挑战,这就迫切要求研究者们提出新的方法来处理超高维数据的降维问题。此外,在生物医学领域和临床试验中,响应变量通常会因为研究对象失联、研究截止时个体仍然存活等原因无法被完全观测,成为右删失的生存数据,处理超高维完全数据的特征筛选法在生存数据中将不再适用,所以寻找一种可以处理超高维右删失数据的稳定性降维方法显得尤为重要。

本研究提出一种能有效处理超高维右删失数据的特征筛选方法,该方法利用距离相关系数刻画每个协变量和响应变量间的边际效应,并建立与该系数相关的筛选指标,最后根据确定的筛选准则进行特征筛选。一方面,在有关超高维删失数据特征筛选方法的研究中,大多筛选方法都是在一些参数或非参数模型的基础上提出的,由于超高维数据复杂程度高,通常情况下难以确定其真实分布,从海量数据集中指定一个具体模型十分困难,一旦模型出错,后续的筛选和分析都会受到影响。提出的特征筛选方法不依赖模型假定,可以有效避免模型误判带来的不良后果。另一方面,采用的距离协方差估计量是总体距离协方差的一个无偏估计,与其他方法相比计算精度和统计准确性更高。此外,数据删失或异常值的存在可能会导致筛选结果出现很大偏差,提出的方法可以在响应变量存在删失和协变量被异常值污染时仍以趋近于1的概率保留所有重要协变量。

1 国内外研究现状

特征筛选是目前最常见也是最有效处理超高维数据的降维方式。目前国内外已有大量关于特征筛选方面研究成果。Fan和Lv(2008)[1]基于线性模型假定首次提出确定性独立特征筛选方法SIS,该方法通过每个协变量与响应变量间的皮尔逊相关系数度量协变量的重要程度,在一定的正则条件下该方法满足确定筛选性。SIS的提出为使用边际相关系数来区分与响应变量“相关”和“不相关”的协变量奠定了基础,后续绝大多数筛选方法都借鉴了SIS的思想,并从不同角度对它进行了拓展和改进。如有的学者解除了SIS线性模型的限制,提出了广义线性模型(Fan和Song,2010)[2]、可加性模型(Fan等,2011)[3]、变系数模型(Fan等,2014)[4]下的独立特征筛选方法,有的学者则采用了其他边际相关系数,如距离相关系数(Li等,2012)[5]和Kendall’s相关系数(Song等,2014)[6]。然而,这些特征筛选过程都事先对模型结构作出了假定。超高维数据的结构十分复杂,从这样复杂、庞大的数据集中找到一个具体模型结构具有挑战性,一旦模型出错,后续的筛选结果和分析过程都会受到影响。来鹏等(2018)[7]针对多分类的响应变量,提出了一种改进的基于条件分布的无模型特征筛选方法,该方法对服从重尾分布的协变量有较好的稳健性。针对超高维数据判别分析中的特征筛选问题,何胜美等(2020)[8]在不需要特定模型假设和有限矩条件限制下,提出一种特征筛选方法,该方法基于秩能量矩,适用于多分类因变量情形,用以筛选类别间分布存在明显差异的协变量。为减少样本比例不平衡和数据异质性在降维过程中产生的不良影响,何胜美和王响(2021)[9]通过最大化条件分布函数的加权C-V-M距离刻画协变量对响应变量的边际效用,提出基于最大边际效用的SAD-SIS筛选法。

在生物医学和临床试验中,研究对象在实验期间失联、实验截止前提前退出、实验结束后存活等行为会导致其生存时间无法被准确记录,成为右删失的生存数据,在有关超高维生存数据的降维方面,一些学者提出了新的筛选方法。Gorst-Rasmussen和Scheike(2013)[10]基于FAST统计量提出单指标危险率模型下的特征筛选方法,FAST统计量是一个简单的线性统计量,由每个协变量与协变量平均值的差值乘以生存时间聚合而成,该方法借助FAST统计量刻画了每个协变量对响应变量的边际效应。基于FAST统计量的独立特征筛选方法可视为SIS方法在右删失数据中的延伸,尤其是在单指标危险率模型的背景下,基于FAST无模型统计量的独立特征筛选方法满足SIS的确定筛选性。与完全数据一样,超高维生存数据中,基于特定模型提出的特征筛选方法受到模型结构影响,其在某些情形下的表现会缺乏稳健性,因此学者们针对生存数据提出一些不依赖模型的特征筛选方法。Song等(2014)[6]提出一种不依赖模型的删失秩独立特征筛选方法,该方法中的秩统计量可视为逆概率加权后的Kendall’s相关系数,利用该系数估计值的大小保留与生存时间边缘秩相关性较强的协变量。在回归分析中,我们常用相关系数衡量两个随机变量间相关性的大小,基于这一思想,Zhang等(2017)[11]根据相关性排序提出一种新的无模型特征筛选方法,该方法通过各协变量与响应变量分布函数的协方差刻画单个协变量的边际效应,其不涉及任何非参数逼近和计算,所以计算简单便捷,运行速度快。然而,这两种处理删失数据的变量筛选方法均需采用Kaplan-Meier估计处理右删失数据,对删失率较高的情形有一定的弊端。

Székely等(2007)[12]提出距离相关系数的概念,用以度量两个随机变量的依赖程度,距离相关系数有两条优良性质。一是距离相关系数是皮尔逊相关系数绝对值的严格增函数,线性模型背景下,若响应变量与协变量均服从正态分布,基于距离相关系数的特征筛选等价于SIS方法。二是两个随机变量相互独立时,它们的距离相关系数为零。这些性质使得它可以用来进行特征筛选。因此,基于Székely等(2007)[12]的距离相关系数,Li等(2012)[5]提出一种不依赖模型结构的特征筛选方法,该方法能很好处理分组协变量或响应变量为多元情形下的特征筛选。Zhang等(2021)[13]提出一种标准化后的基于距离相关的无模型特征筛选,该方法中响应变量由标准化后的观测时间和删失示性变量组成,通过计算每个协变量与二元响应变量的距离相关系数,对协变量重要程度进行排序。在响应变量存在删失或协变量存在异常值时,该方法的表现显著优于其他方法。然而,上述基于距离相关的特征筛选,距离相关系数估计量均采用了Székely等(2007)[12]的计算方式。本研究基于Székely和Rizzo(2014)[14]提出的距离相关系数估计量提出一种不依赖模型的独立特征筛选方法,通过非线性、Cox比例风险、转换模型三种模型和Python中的random包随机产生满足设置要求的实验数据,模拟随机和非随机两种删失机制和协变量存在异常值的各种情形,并依据模拟结果对不同筛选方法的筛选性能进行比较分析,从而验证提出方法在变量选择中的优势。最后将提出的筛选方法应用于对弥漫大B细胞淋巴瘤患者生存结果有显著影响的基因筛选之中,进一步说明提出方法在实际应用中的可行性。

2 基于距离相关的Model-Free特征筛选

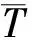
I={k:S(t|X)依赖于Xk,k=1,…,p}.

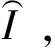
Székely等(2007)[12]提出距离协方差的概念,并利用距离协方差测度两个随机变量间的独立性。给定两个随机变量x∈Rdx和y∈Rdy,两者之间的距离协方差dcov(x,y)的平方定义为

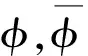
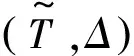
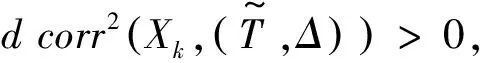
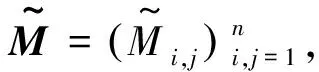
(1)

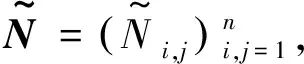
(2)

由式(1)和(2),Székely和Rizzo(2014)[14]给出距离协方差平方dcov2(Xk,Y)的一个估计如下:

(3)

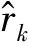
(4)

其中c和κ是已知常数,称由式(4)定义的筛选方法为基于距离相关(3)排序的独立筛选法,简记为bcDC。由Fan和Lv (2008)[1]可知,可以采取如下重要协变量下标估计式的定义方式进行变量筛选,即事先设定一个正整数d0=「n/logn⎤,

3 数值研究

本节评估基于距离相关的Model-Free筛选方法bcDC在有限样本下的表现,并将其与现有方法进行比较。为了描述方便,将对比的方法,即Gorst-Rasmussen和Scheike(2013)[10]、Song等(2014)[6]、Zhang等(2017)[11]和Zhang等(2021)[13]提出的方法分别简记为FAST、CRIS、CR-SIS、CDCS。采用以下5个标准评估不同方法的筛选性能。

1)最小模型大小S:所有重要协变量被包含在选出的模型中所需要保留协变量个数的最小值。

本研究采用500次数值模拟最小模型大小的中位数(Med)和四分位距(IQR)两个指标进行描述。

2)Pe:对于给定的模型大小「n/logn⎤,500次数值模拟中每个重要协变量被挑选出来的概率。

3)Pa:对于给定的模型大小「n/logn⎤,500次数值模拟中所有重要协变量均被挑选出来的概率。

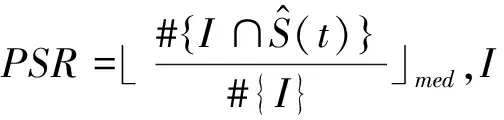
其中,#{·}表示集合中元素个数,⎣·」med表示序列值的中位数。

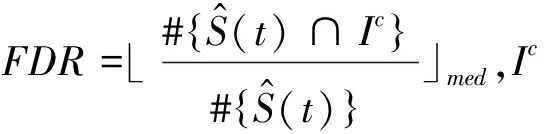
显然,Med的值越接近真实重要协变量集的元素个数,IQR值越小,Pe、Pa和PSR越接近于1,FDR越接近于0,证明对应的特征筛选方法越好。为检验bcDC筛选方法的稳健性,不仅考虑随机删失和非随机删失两种删失机制,还考虑某些协变量存在异常值的情形。基于非线性模型、Cox比例风险回归模型和转换模型3种不同模型设置产生数据进行模拟。

3.1 非线性模型假设生存时间T产生于一个非线性模型,其与协变量X和随机误差项ε满足下列关系式:

logT=1-5(X2+X3)-3exp{1+10sin(πX1/2)+5X4}+ε,

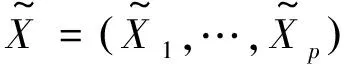
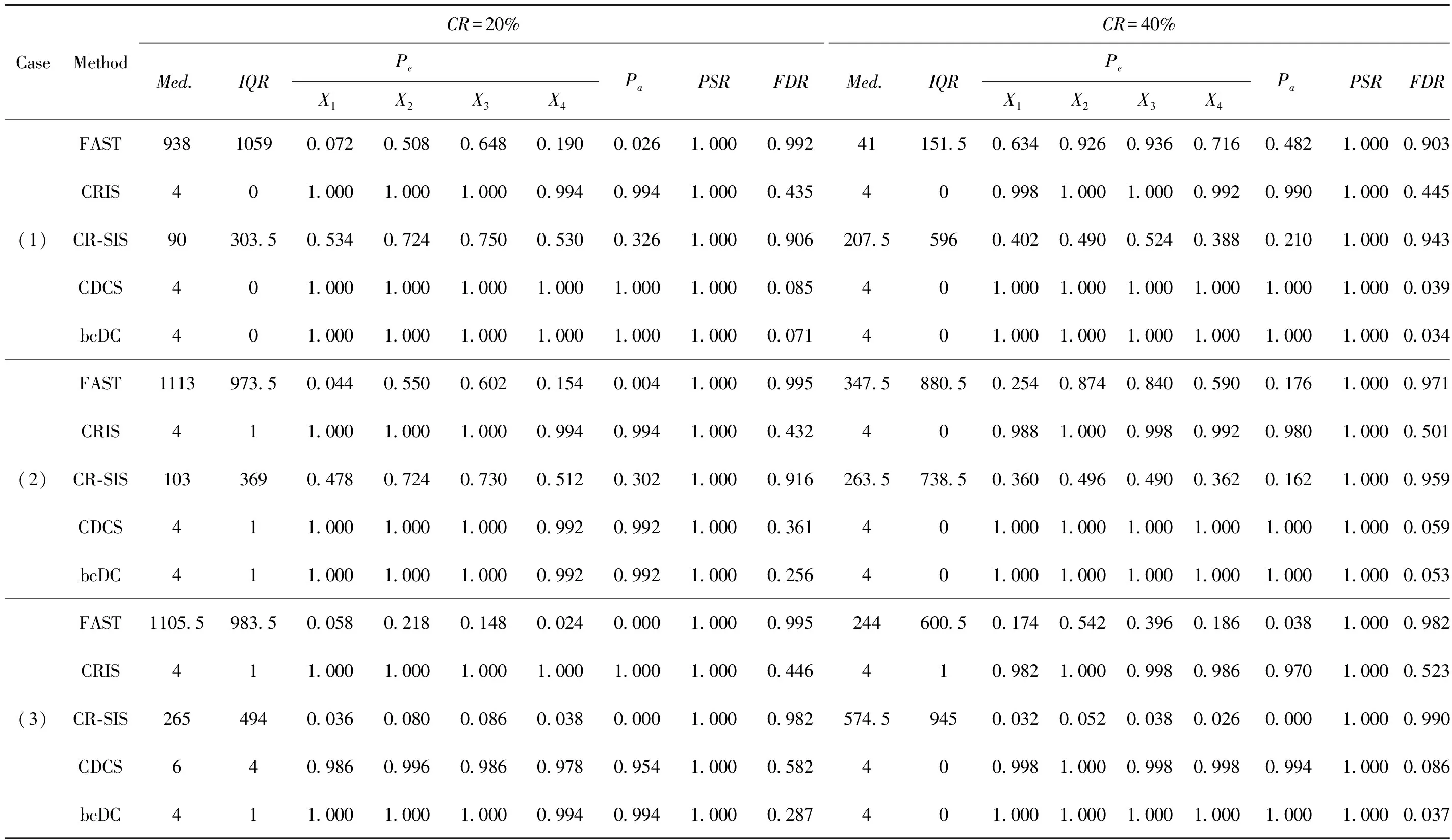
表1 非线性模型下数值模拟结果

从表1可以看出:在非线性模型背景下,不论是响应变量随机删失还是非随机删失,bcDC的表现显著优于FAST和CR-SIS两种方法,其变量正确选择率PSR为100%,500次数值模拟结果显示,bcDC最小模型大小S的中位数为真实模型大小4,四分位距趋近于0,Pa值趋于1,说明不论在上述何种设置下bcDC筛选性都能保持稳定。此外,当协变量存在异常值点时,FAST和CR-SIS方法失效,最小模型大小S的中位数非常大,远远超过真实模型大小,Pe和Pa趋近于0,错误发现率FDR高达90%以上,而基于距离相关的CDCS和bcDC表现依旧稳健,且bcDC相较于CDCS的FDR更低。

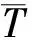
λ(t|X)=λ0(t)exp(XTβ0),

其中基准风险函数λ0(t)=(t-0.5)2,X=(X1,…,Xp)T～Np(0,∑),∑=(0.8|i-j|)(i,j=1,…,p),真实参数β0=(0.35,0.35,0.35,0.35,0.35,0p-5)T,即只有前5个协变量是重要协变量。其他设置与非线性模型设置保持一致,500次数值模拟实验结果如表2所示。

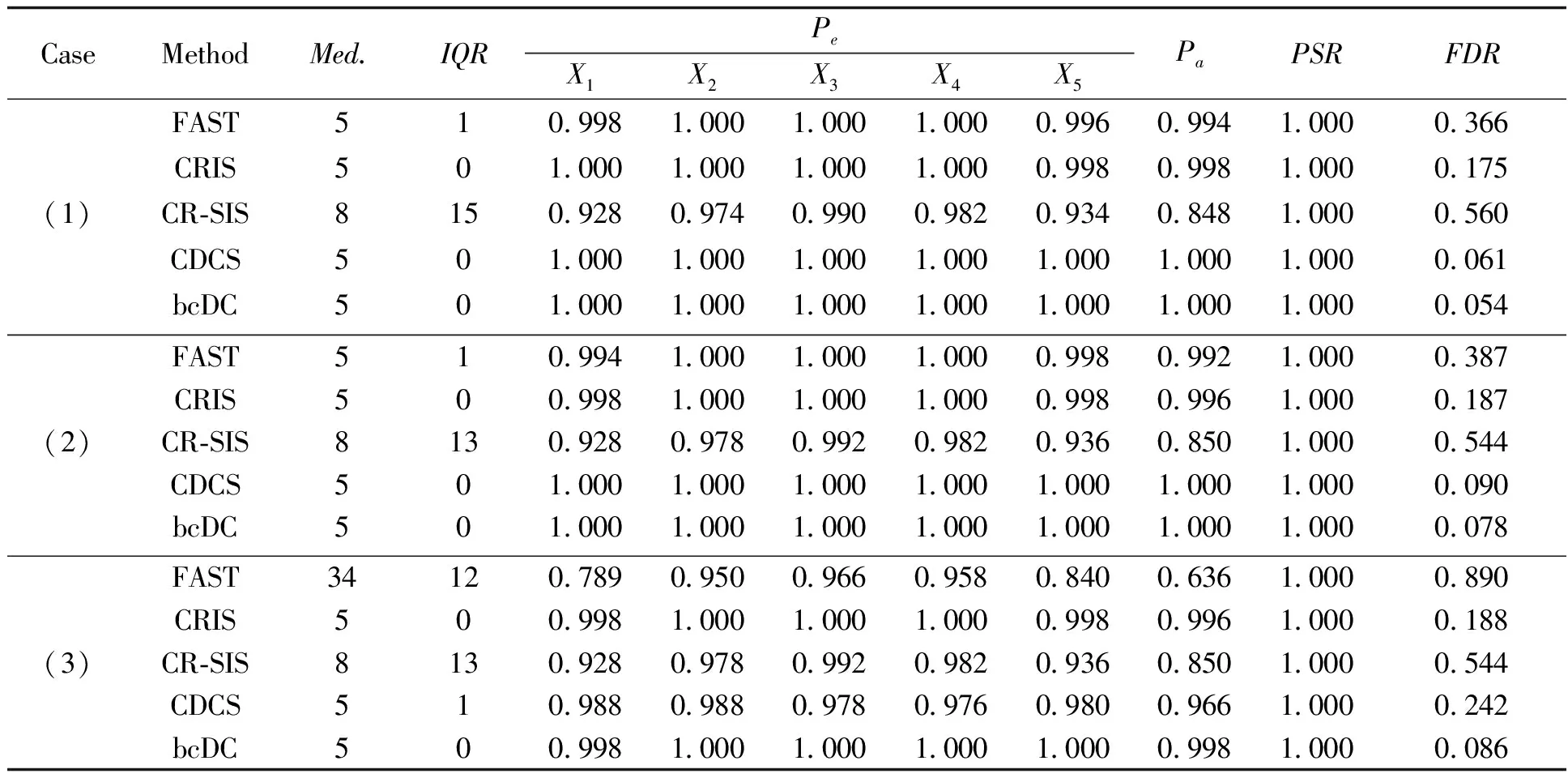
表2 Cox比例风险模型下数值模拟结果(CR=20%)

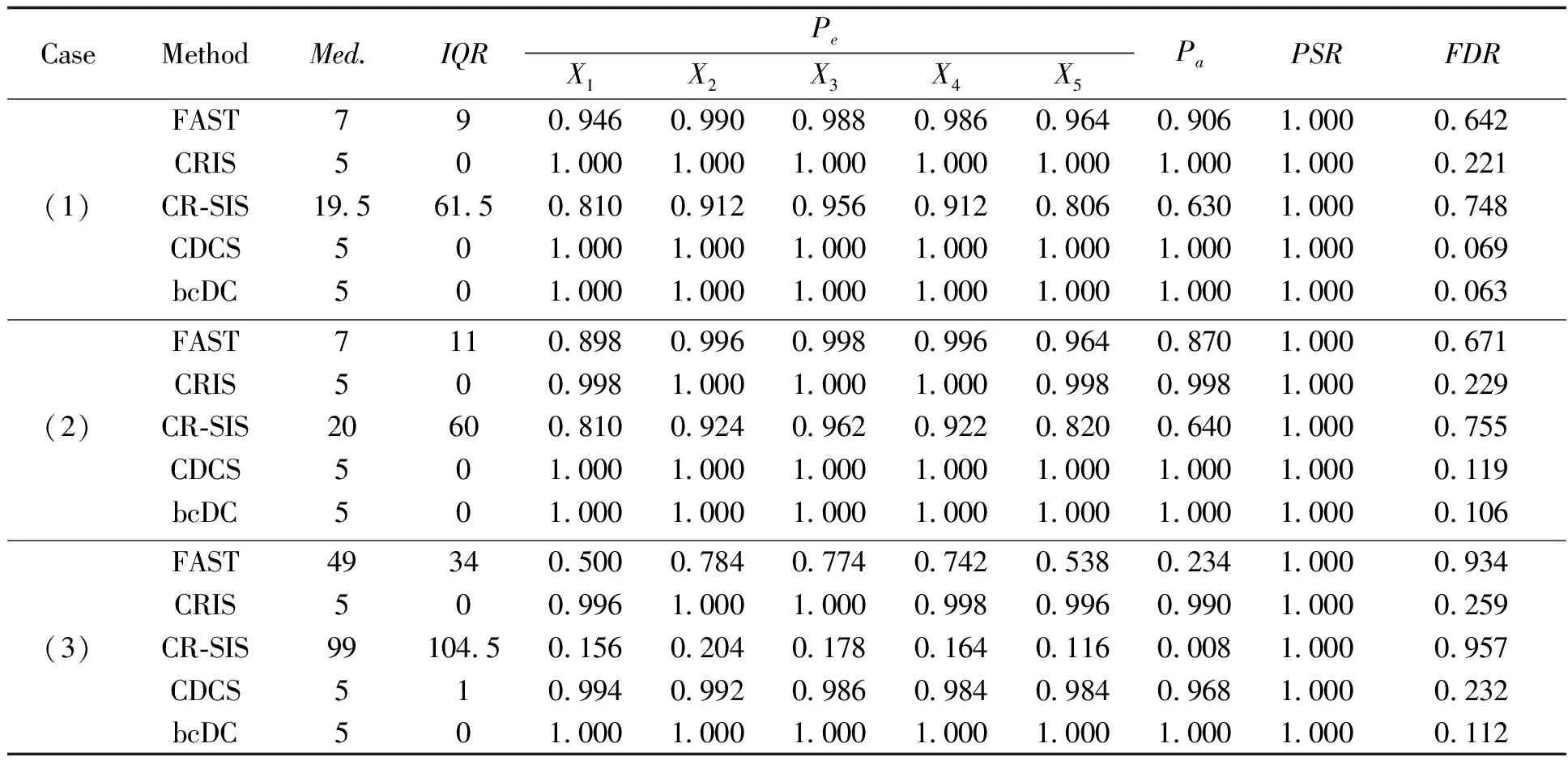
表3 Cox比例风险模型下数值模拟结果(CR=40%)

从表2～3可以看出:当协变量不存在异常值时,5种方法均表现良好,变量正确选择率PSR为100%,除CR-SIS外,其他四种方法每次都能以趋近1的概率保留所有重要协变量,最小模型大小S的中位数近乎接近真实模型大小5。当协变量存在异常值时,基于Cox比例风险模型的FAST和CR-SIS方法筛选性能下降,Pa有时会降至0.3以下,当删失率为40%时,FDR有时会趋近90%以上,说明这两种方法在500次数值模拟中绝大多数时刻都无法完整、准确的保留所有重要协变量。基于距离相关的CDCS和bcDC方法的表现则相对稳健,每次都能以95%以上的概率保留所有重要协变量,并且bcDC的错误发现率FDR比CDCS方法要低。

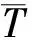
H(T)=-β0X+ε,

其中函数H(t)=log(0.5(e2t-1)),协变量X～Np(0,∑),∑=(0.8|i-j|)(i,j=1,…,p),真实参数β0=(-1,-0.9,06,0.8,1.0,0p-10)T。假定随机误差项ε是由3种不同分布生成,即标准正态分布,标准柯西分布和标准logistic分布。其他设置与非线性模型设置保持一致,500次数值模拟结果如表4～5所示。

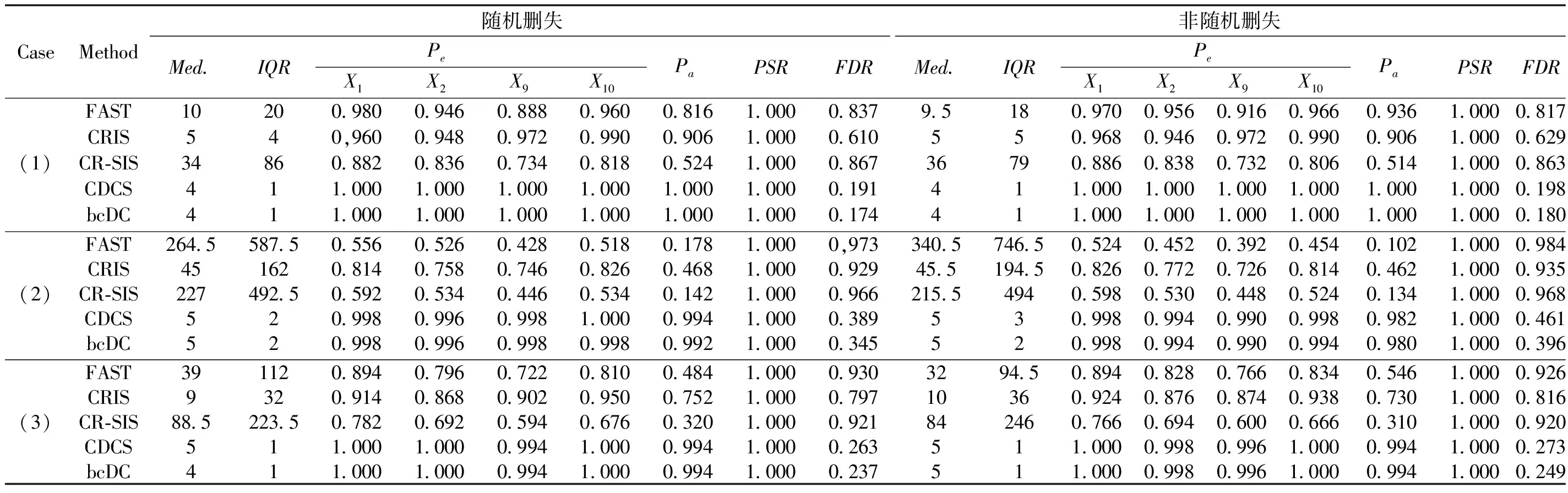
表4 转换模型下数值模拟结果(CR=20%)

通过观察表4～5响应变量在不同删失机制下各方法的筛选结果发现:FAST、CRIS和CR-SIS这3种方法在筛选变量过程中几乎失效,CDCS和bcDC显著优于FAST、CRIS和CR-SIS方法。不论响应变量存在20%删失还是40%删失,bcDC和CDCS最小模型大小S的中位数均接近真实模型大小4,变量正确选择率达到100%,并且在500次数值模拟研究中能以99%以上的概率保留所有重要协变量,但bcDC错误发现率FDR比CDCS的更低,表现更加稳健。

4 实例分析

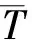
为了对比不同筛选方法的表现效果,除考虑bcDC方法外,还考虑Gorst-Rasmussen和Scheike(2013)[10]提出的FAST方法,Song等(2014)[6]提出的CRIS、Zhang 等(2017)[11]提出的CR-SIS和Zhang等(2021)[13]提出的CDCS方法。利用这5种方法从7 399个基因中筛选出[240/log(240)]=43个重要基因。通过bcDC方法筛选出的基因与其他方法筛选出的基因重合率很高,如bcDC方法筛选出的43个重要基因中,有42个基因在不基于模型的CR-SIS和CRIS方法中同样也被筛选出来,由于表格过大,在此不再展示基因编号。为进一步分析数据,根据bcDC筛选出的协变量拟合Cox比例风险模型,利用正则化方法LASSO、SCAD和MCP从预先选出的43个协变量继续筛选变量,通过十倍交叉验证选择调整参数。基因选择结果和相应回归系数估计值如表6所示。

表6 基于LASSO、SCAD、MCP重要基因筛选结果

从表6可以看到,43个重要基因中,有6个基因31981、24376、32238、28641、28532、27592被LASSO、SCAD、MCP共同选中,说明这6个基因对病人的生存结果有重大影响。此外,观察回归系数估计值可以发现,31981基因对病人生存结果影响最大,这一结果与Li和Luan(2005)[16]和Zhang等(2021)[13]的结论一致,他们同样将31981基因放在所有对病人生存结果具有重大影响基因的首位。

为进一步评估bcDC方法的预测能力,将240个样本随机划分成n1=160的训练集和n2=80的测试集,训练集中的数据用于建立患者生存风险预测模型,测试集中的数据用于模型预测能力的评估。DLBCL生存时间摘要如表7所示。

表7 DLBCL数据集生存时间统计表

本文中首先将bcDC方法用于训练集,筛选出[160/log(160)]=31个重要基因,然后利用选出的31个基因拟合Cox比例风险模型,计算回归系数的估计值;在测试集中计算每个患者的风险得分,根据风险得分估计值的平均值将患者分为高、低风险组两组。图1描绘了bcDC方法下Kaplan-Meier生存曲线,可以观察到:低风险组和高风险组的生存曲线可以很好地分离开来。

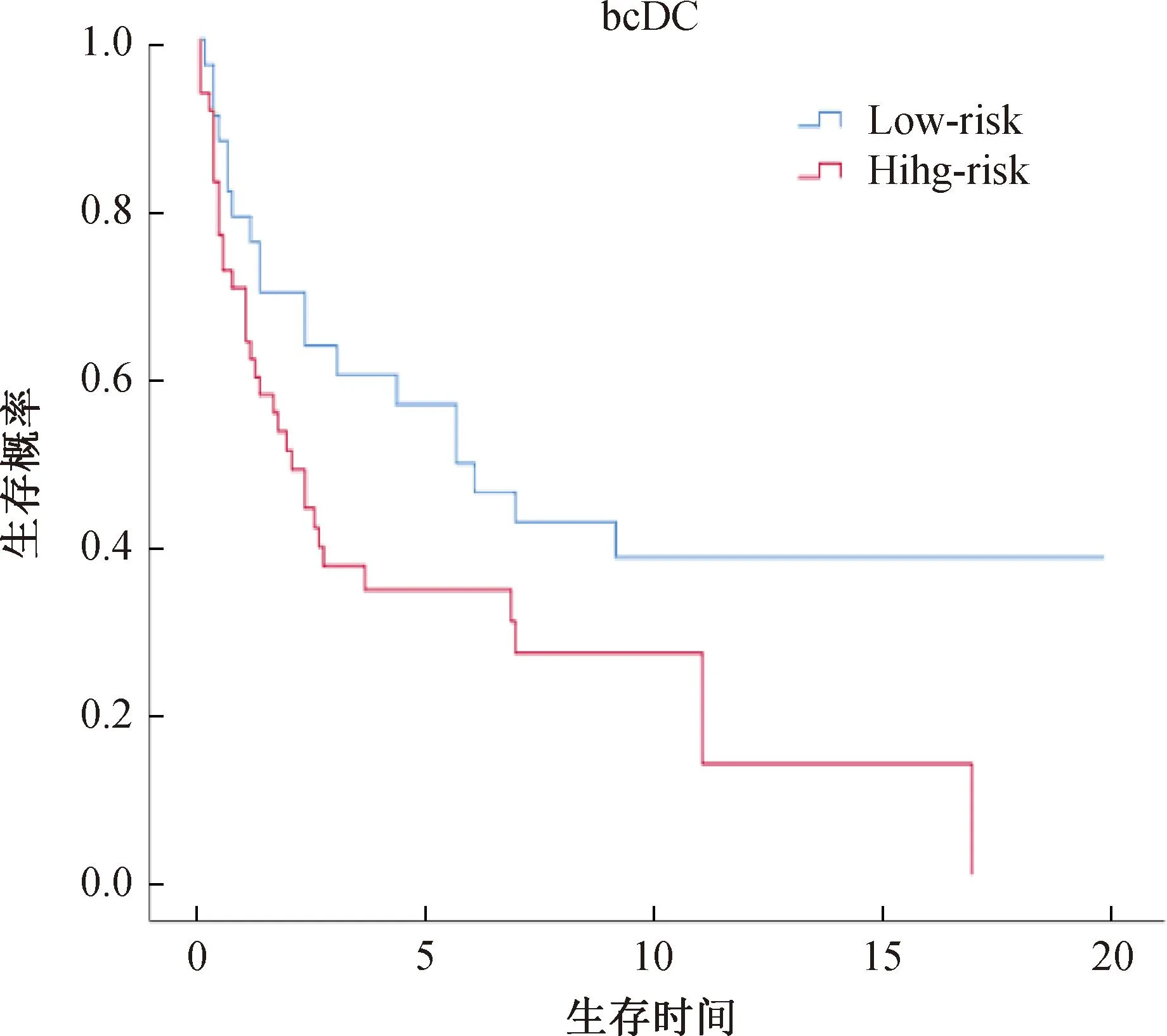
图1 生存时间的Kaplan-Meier曲线

为使结果更具有说服力,进一步进行了log-rank检验,检验两条生存曲线是否存在显著差异,bcDC方法log-rank检验的p值为0.045<0.05,说明基于bcDC建立的预测模型具有较好的预测能力,可以采用提出的bcDC方法建立预测模型预测未来患者死亡的风险。

5 结论

针对超高维生存数据,基于距离相关系数,提出了一种不依赖模型的特征筛选方法bcDC,该方法不涉及生存时间的Kaplan-Meier估计或复杂的数值优化过程,实施起来较为迅速与便捷。bcDC允许协变量的维度随着样本量指数阶增长,而且能以较高的概率在保留所有重要变量的前提下快速有效的降低数据的维度。模拟研究表明,在非线性模型、Cox比例风险回归模型和转换模型3种不同模型设置下,当响应变量存在删失或协变量存在异常值时,bcDC方法均能以趋近1的概率保留所有重要协变量并且错误发现率也较低。尤其是在非线性模型中,与FAST、CRIS、CR-SIS相比,bcDC能更好地筛选出超高维生存数据的重要变量。实证研究表明bcDC方法具有可实施性,通过该方法筛选出的变量建立的预测模型预测效果较好。