弱电网下抑制谐波谐振的LCL型并网逆变器鲁棒性CCFAD方法
杨明, 杨杰, 赵铁英, 郑晨, 韦延方
(1.河南理工大学 电气工程与自动化学院,河南 焦作 454003; 2.河南省电力公司电力科学研究院,河南 郑州 450052)
0 引 言
LCL型并网逆变器是连接可再生能源发电单元与电网的关键接口设备,用来将直流电能转化为高质量的交流电能并馈入电网,其性能优劣对入网电能质量具有重要影响[1-2]。然而,LCL滤波器是一个欠阻尼三阶系统,其固有的谐振尖峰易引发控制系统失稳[3]。通常,对谐振尖峰的阻尼方式可分为无源阻尼与有源阻尼两种。其中,无源阻尼是在滤波器的滤波元件两端并联或串联无源电阻器,该方式具有可靠性强、实现简单等优点,但会产生不同程度的功率损耗,而在滤波电容两端串联无源电阻器因其功率损耗较小被广泛应用[4]。为进一步减小无源阻尼带来的功率损耗,可将无源阻尼方式通过反馈控制相应的电流或电压状态变量进行等效实现,便产生了有源阻尼方式,其中,电容电流比例有源阻尼方式不会改变滤波器在低频域和高频域的幅频衰减特性,被大范围推广使用,这与电容两端并联电阻的无源阻尼方式是等效的[5-8]。
然而,随着数字控制技术的发展,数字控制延时将对并网逆变器控制系统的稳定性运行产生威胁。一般,系统常采用不对称规则采样方式进行脉冲宽度调制,会引入1.5拍的等效控制延时[9]。此时,电容电流有源比例有源阻尼回路等效为并联在滤波电容两端的虚拟阻抗,控制延时的存在导致该虚拟阻抗在一定频域范围内呈现负阻特性,造成并网逆变器对弱电网下较宽范围变化的电网阻抗鲁棒性较差[10]。当系统稳定裕度降低时,电网电压中含有的背景谐波电压将在并网电流中得到放大,甚至引发谐波谐振,劣化入网电能质量,严重威胁并网系统的稳定运行。
目前,针对数字控制延时导致系统失稳的问题,已有诸多学者从不同角度加以分析并提出相应的解决方法,主要分为两类:1)改变传统采样方式,减小数字控制延时。例如:双采样模式实时运算方法[11]、及时采样方法[12]、基于过采样的控制方法[13]等减小数字控制延时的举措,可有效改善并网逆变器的稳定性,然而,不同采样方式的实现依赖于高精度的处理设备,增加处理器的运行复杂度,并不利于大规模应用。2)改变传统电容电流比例有源阻尼方式,通过引入具有相位超前环节对控制延时导致的相位滞后进行补偿[14-18]。但相位超前环节往往具有微分特性,即该环节传递函数分子部分的阶数大于等于分母部分的阶数,钳制了该方式实现的灵活性。
综上所述,已有的改善数字控制延时引发并网逆变器稳定性降低的方法,在实现简单化和灵活性上仍有欠缺。鉴于此,本文提出一种利用负一阶惯性环节电容电流反馈有源阻尼(capacitive-current-feedback-active-damping,CCFAD)鲁棒性方法,该方法可有效扩大阻尼环路等效虚拟阻抗的正阻范围,极大地提高并网逆变器对电网阻抗的鲁棒性,并网系统谐波谐振亦得到抑制。此外,该方法具有较好的灵活性,仅通过反馈控制电容电压状态变量,即可实现滤波器的有源阻尼及锁相并网的功能,节省一组电流传感器的使用,降低并网逆变器的硬件成本。
1 LCL型并网逆变器CCFAD控制模型建立
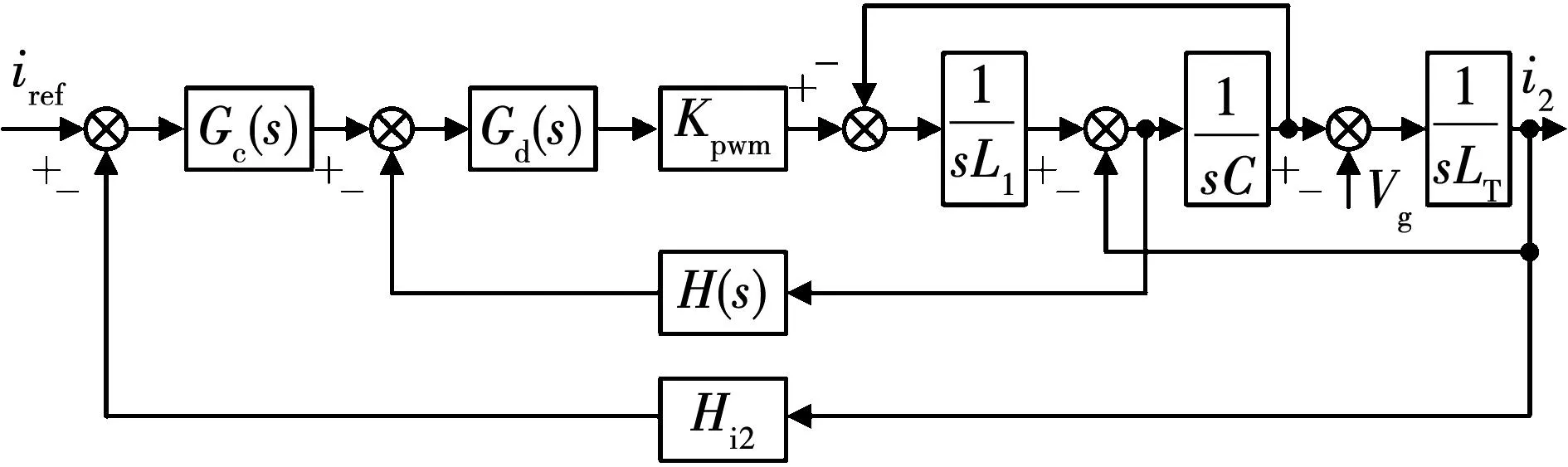
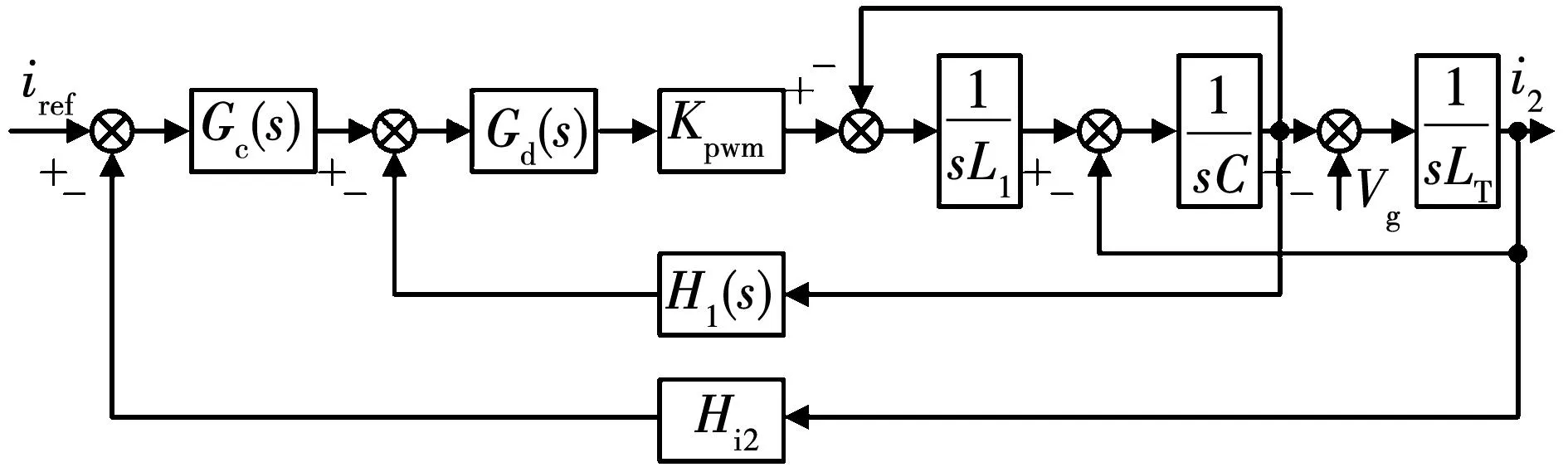
图1为CCFAD双闭环LCL型并网逆变器总体控制结构图。图1中:Vdc为直流侧电压;Cdc为直流侧电容;VPCC和Vg分别代表公共并网点(point of common coupling,PCC)电压与电网电压;逆变器机侧电感L1、网侧电感L2和滤波电容C组成LCL滤波器;ic和i2分别为电容电流与网侧电流;Hi1为电容电流有源阻尼系数;Hi2为网侧电流反馈系数;通常,电网阻抗呈阻感特性,但阻性分量有利于并网系统的稳定性,因此本文仅考虑电网阻抗为纯感抗的最恶劣工况,Lg代表电网等效电感;iref为参考电流信号,由给定参考幅值Iref与锁相环(phase locked-loop,PLL)输出VPCC相位信息sinθ相乘获得;Gc(s)代表准比例谐振(quasi-proportional resonance,QPR)电流控制器的传递函数,表达式为
(1)
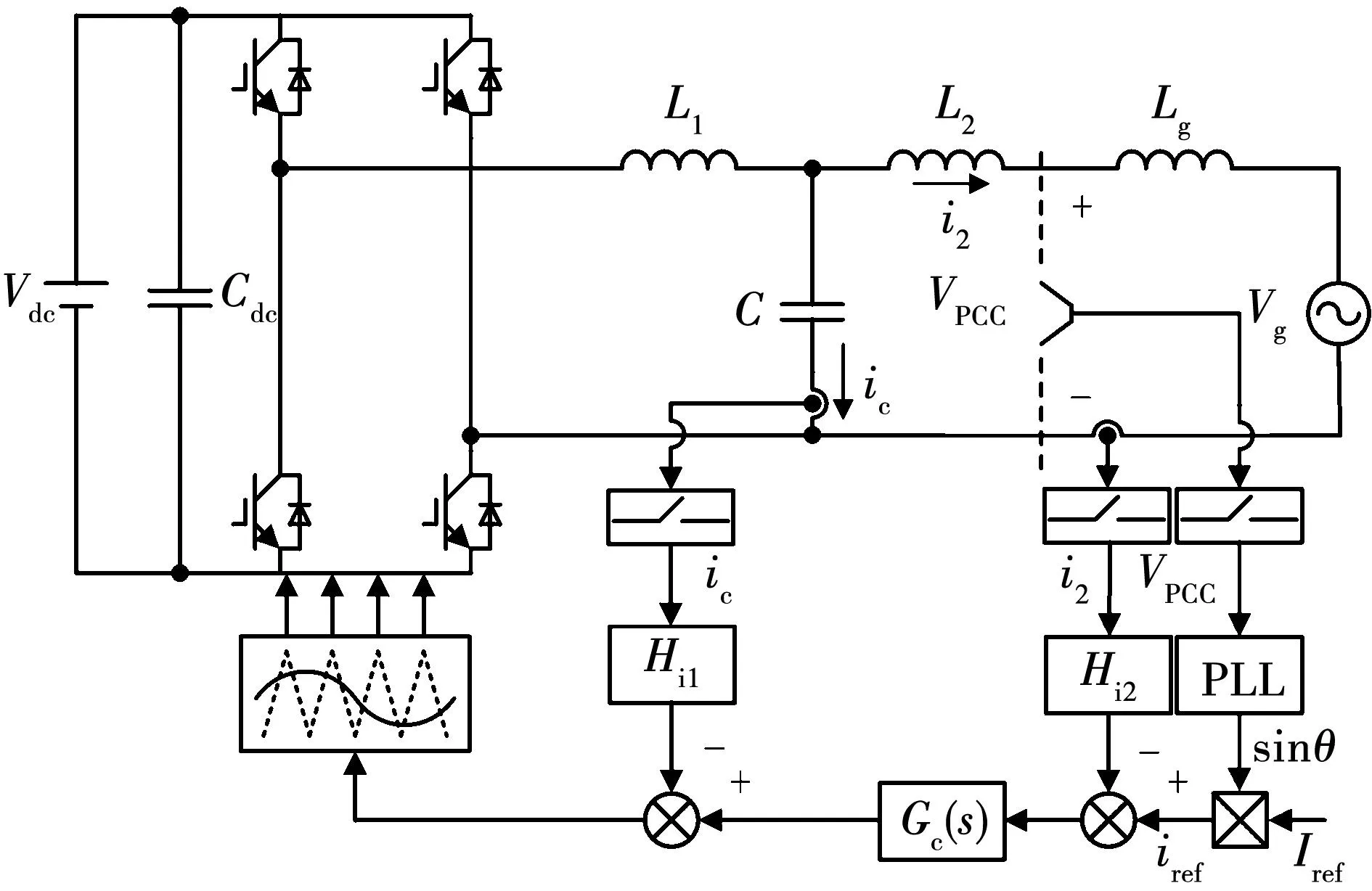
图1 LCL型并网逆变器CCFAD控制结构图
式中:Kp为比例系数;Kr为谐振系数;ω0≈314 rad/s为电网电压基波角频率;ωi代表谐振宽度,为适应电网基频(1±5%)ω0的波动,通常选取ωi=3.14。
根据图1所示总体控制结构图,可以得到如图2所示的LCL型并网逆变器系统结构图。图2中,Kpwm=Vdc/Vtri代表逆变桥等效增益(Vtri为脉冲宽度调制过程中的三角载波幅值);等效电感LT=L2+Lg。为避免开关噪声对控制系统的影响,并网逆变器常采用不对称规则采样进行数字控制,其采样频率fs为开关频率fsw的2倍,这将引入1拍的计算延时与0.5拍的调制延时。Gd(s)代表数字控制延时在s域中的等效传递函数,常近似表示为
(2)
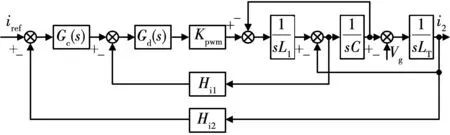
图2 LCL型并网逆变器CCFAD系统结构图
式中Ts代表采样周期。
根据图1可以推导出iref(s)到i2(s)的开环传递函数T0(s),其表达式为
(3)
式中fr代表LCL滤波器的谐振频率,表示为
(4)
为便于后续分析,本文以一台3 kW的单相LCL型并网逆变器为例,主电路参数见表1。需要说明的是,电流控制器Gc(s)仅对开环系统在基频附近的特性产生影响,本文主要分析数字控制延时与电网阻抗交互作用下在高频域对控制系统稳定性的影响,因此后续不考虑电流控制器(Gc(s)=1)的作用。
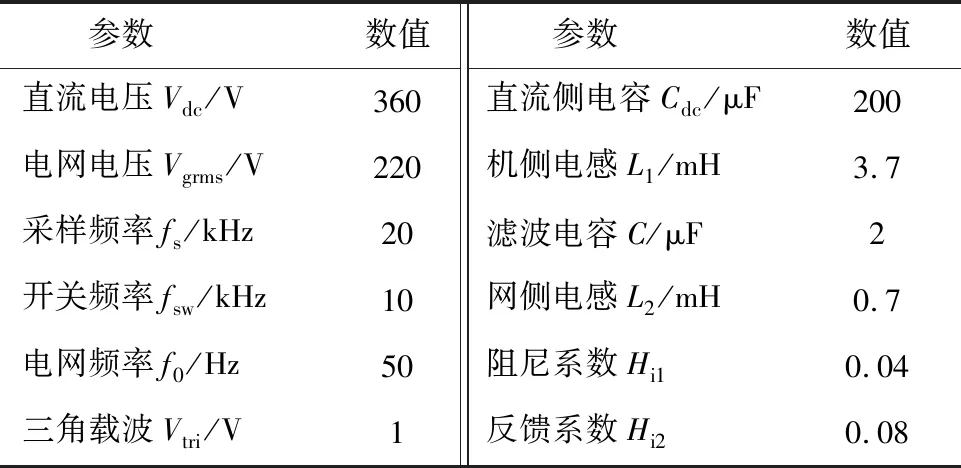
表1 并网逆变器主电路参数
1.1 传统CCFAD控制的稳定性分析
对图2进行等效变换,得到如图3(a)所示的系统结构图。由此可见,CCFAD环路等效为并联在滤波电容支路两端的虚拟阻抗Zeq(s),等效电路模型如图3(b)所示,其表示为
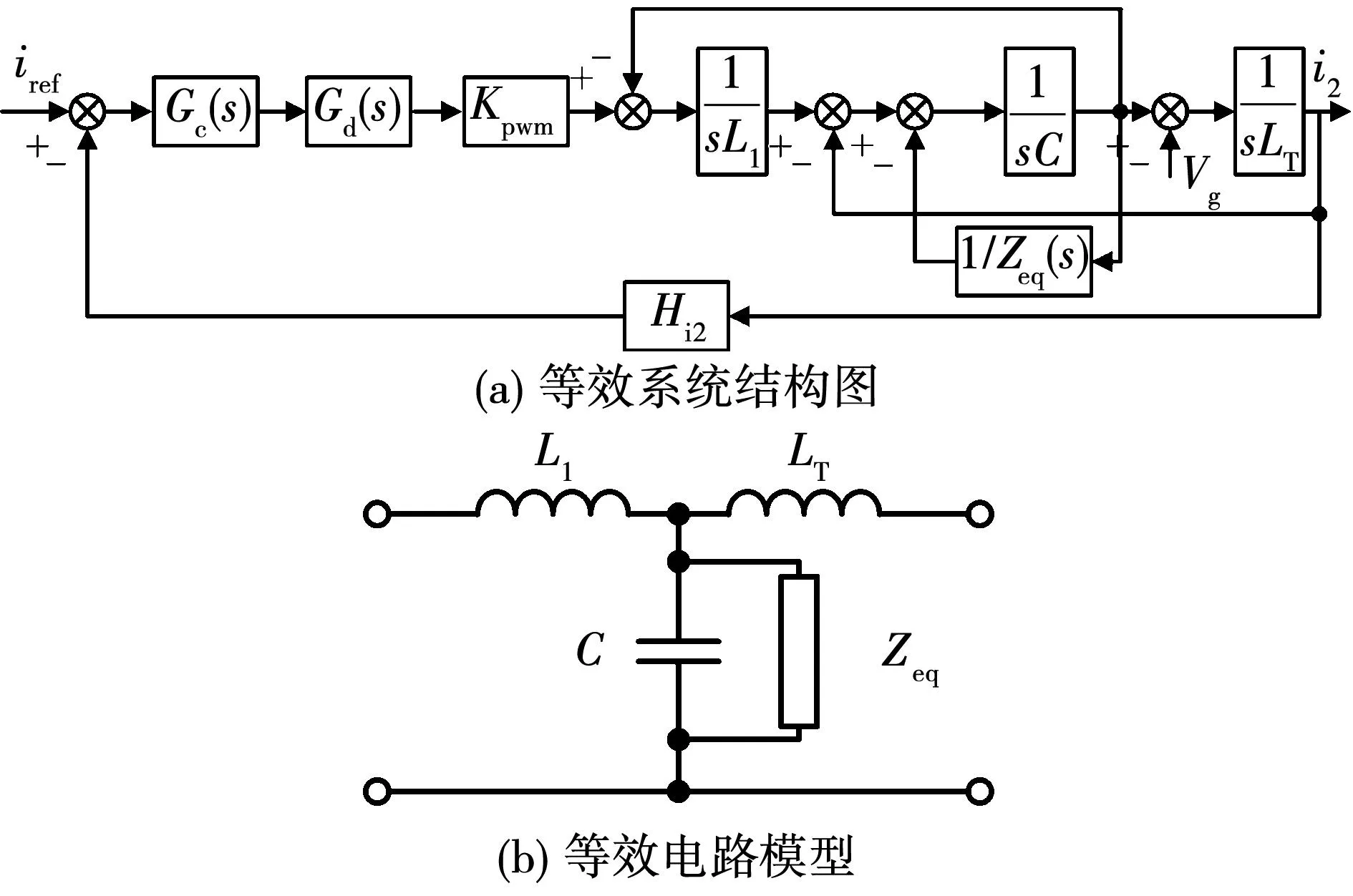
图3 并网逆变器的等效模型
Zeq(s)=RAe1.5Tss。
(5)
式中RA=L1/(CKpwmHi1)
不考虑数字控制延时(Gd(s)=1)的情况下,Zeq(s)为纯电阻RA,等效为滤波电容并联电阻的无源阻尼方式;数字控制延时的引入,Zeq(s)变成一个与频率相关的虚拟阻抗,势必会对控制系统的稳定性造成影响。
令s=jω并代入式(5)得到Zeq(jω),将其等效为虚拟电阻Req(ω)与虚拟电抗Xeq(ω)的并联形式,即Zeq(jω)=Req(ω)//jXeq(ω),Req(ω)与Xeq(ω)的表达式分别为:
(6)
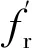
图4 Req(ω)与Xeq(ω)的频率特性曲线
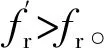
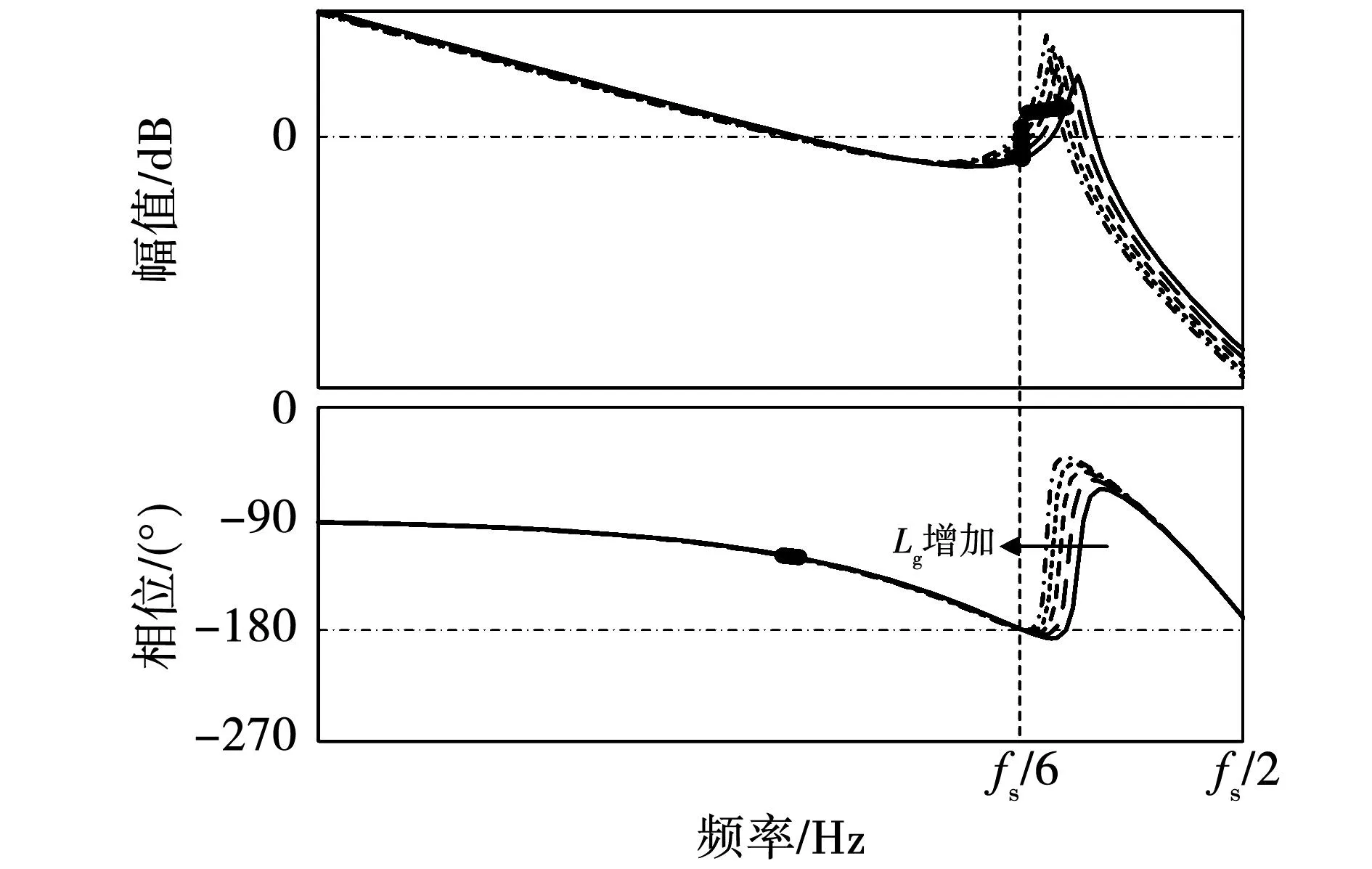
图5 开环传递函数T0(s)的伯德图
分别记T0(s)在fs/6和fr处对应的幅值裕度为GM1、GM2,通过式(3)可以推导出二者的表达式为:
GM1=
(7)
(8)
由此可以绘制出GM1、GM2关于Lg的变化曲线,如图6所示。从图6可以看出,GM1随着Lg的增加逐渐减小,而GM2随着Lg的增加逐渐增大,并且GM1关于Lg的变化速率高于GM2关于Lg的变化速率,即在Lg变化过程中GM1率先为0 dB。令GM1=0 dB,根据式(7)易推导出使系统处于临界稳定状态时Lg的值为
(9)
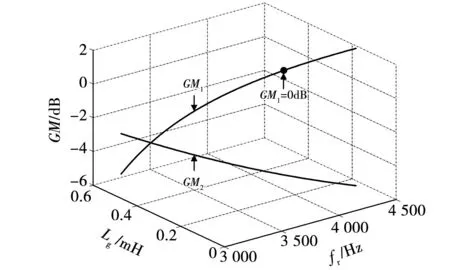
图6 GM1、GM2关于Lg的变化曲线
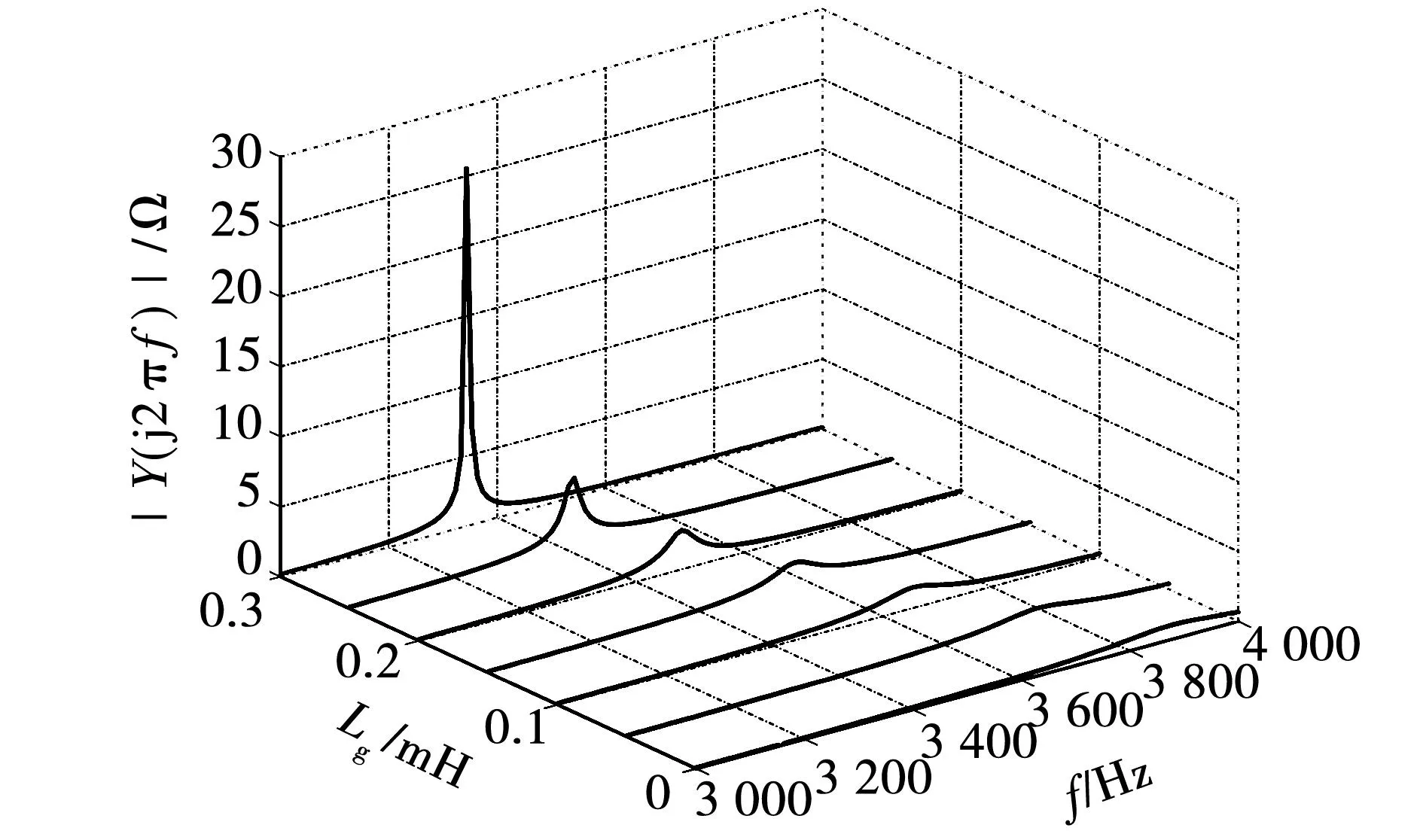
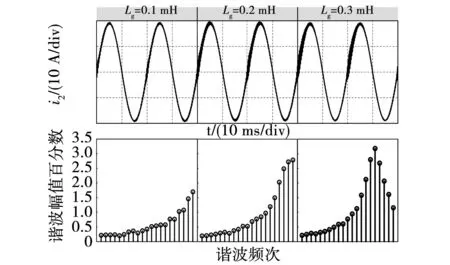
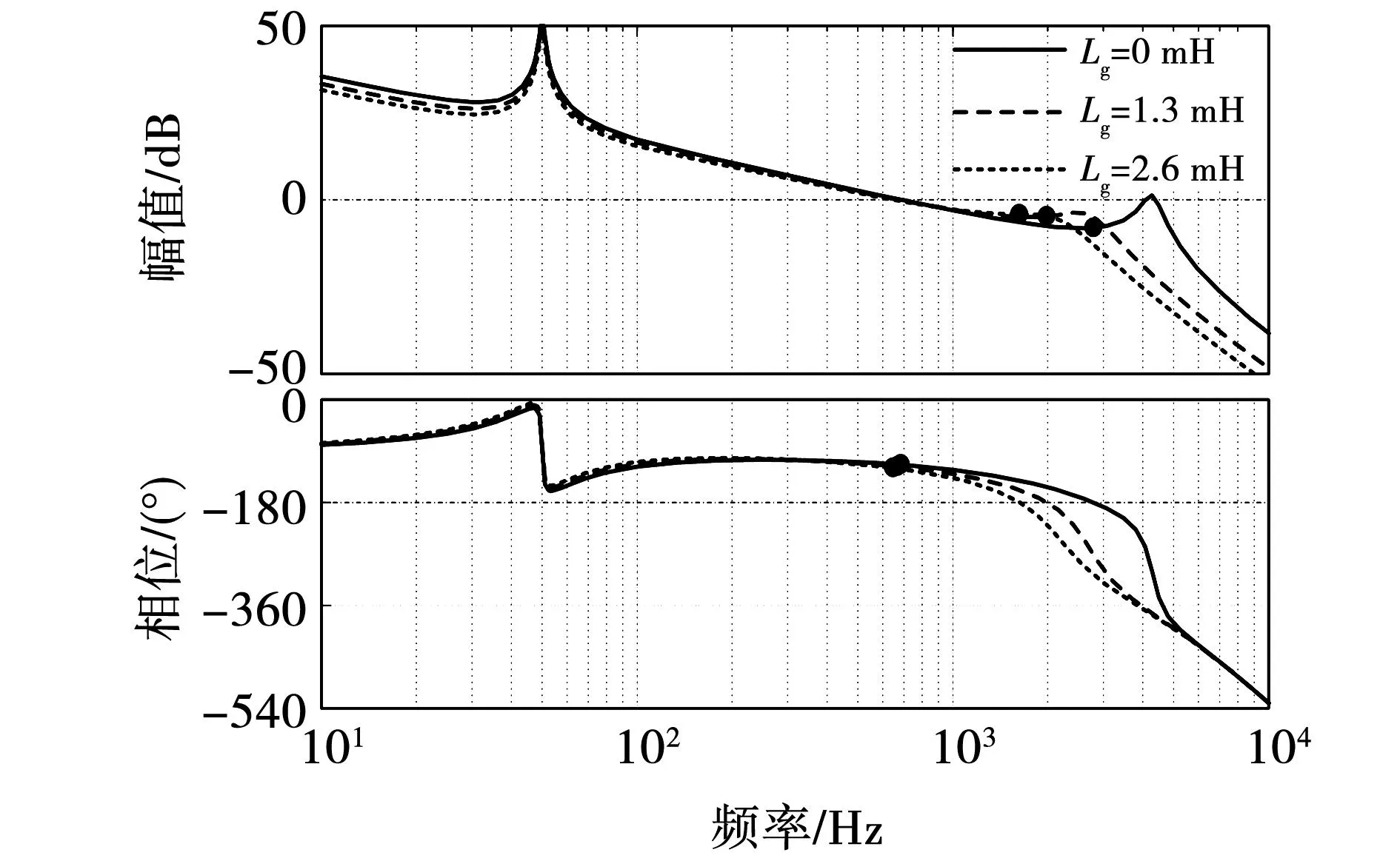
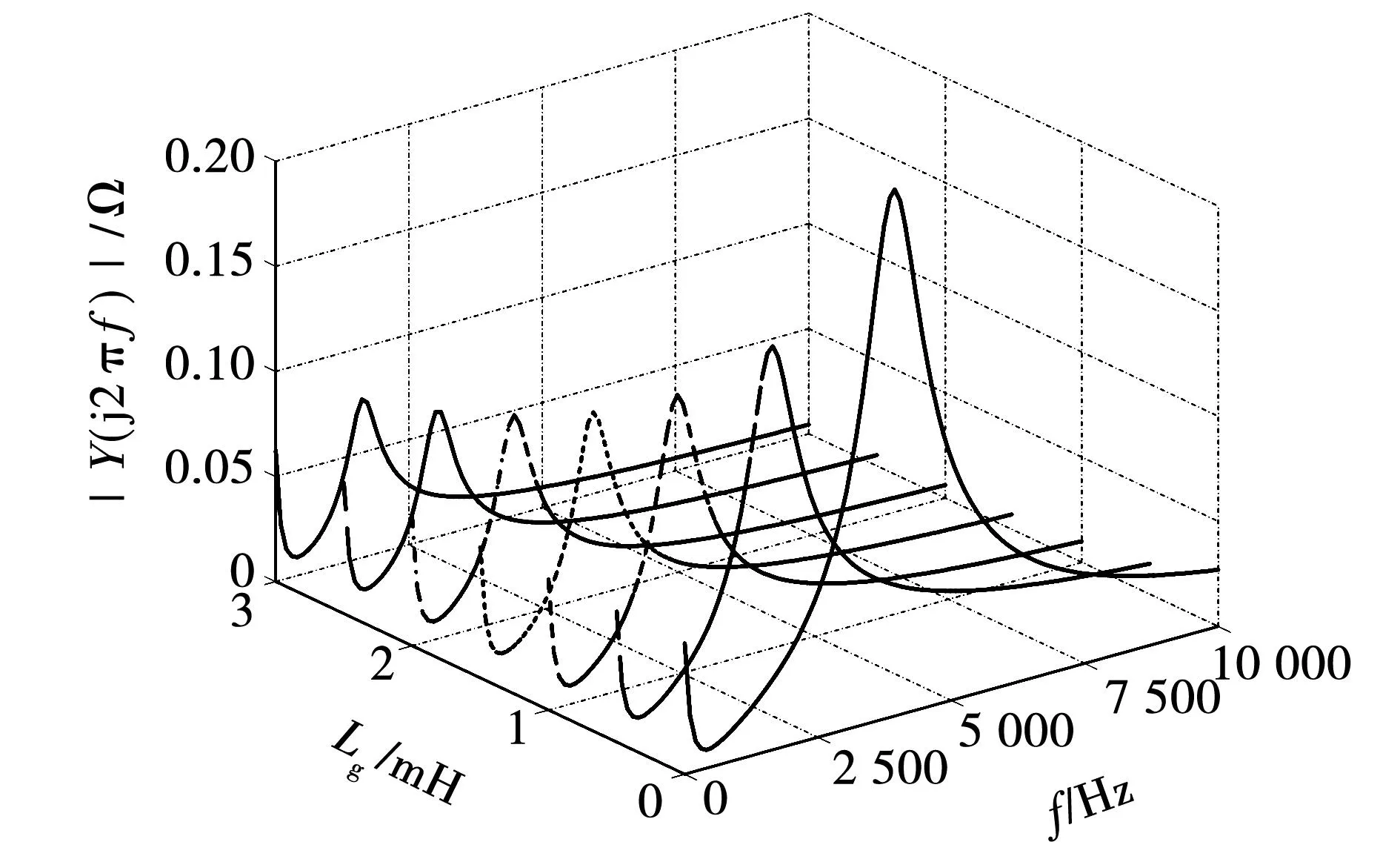
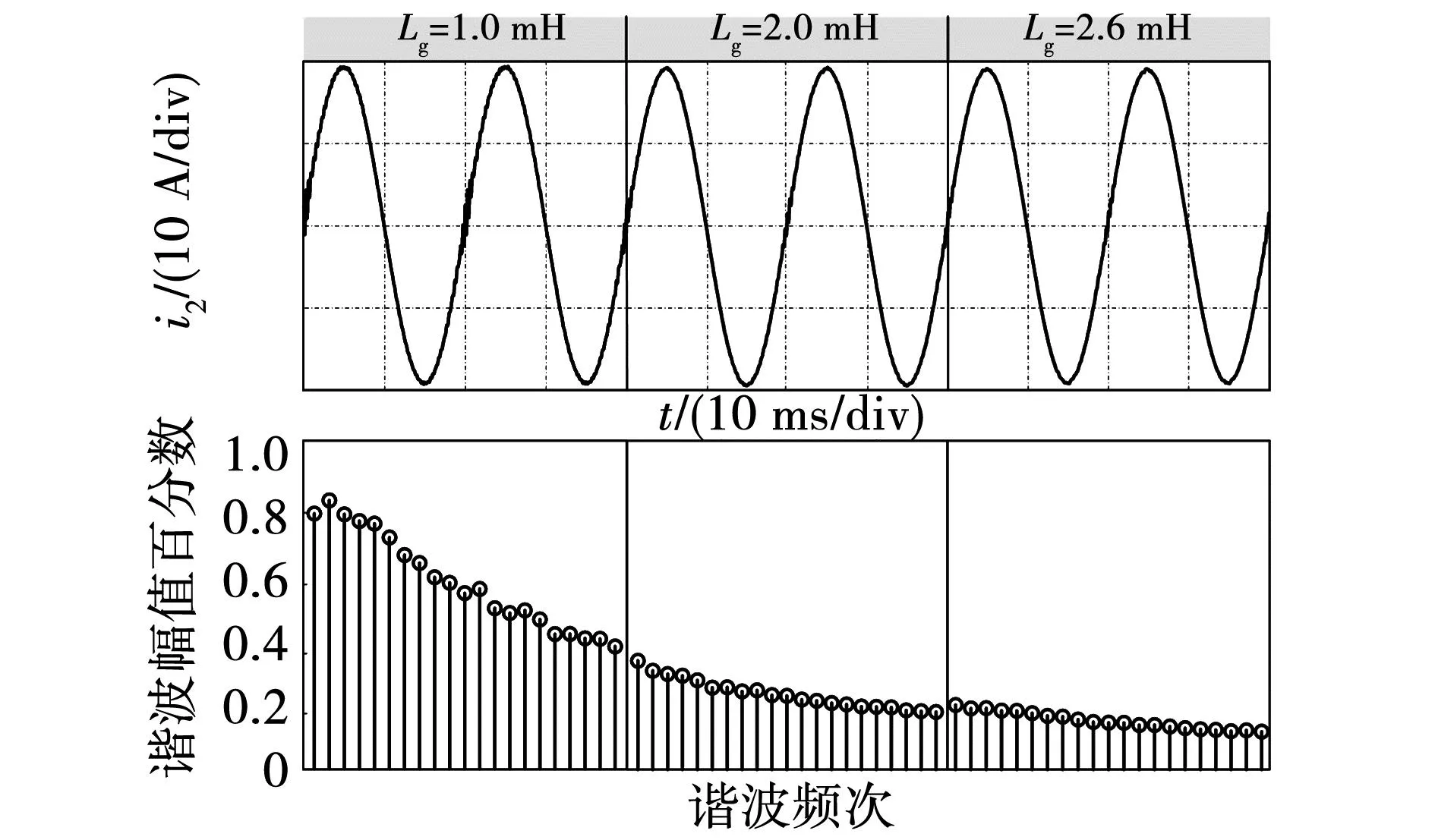
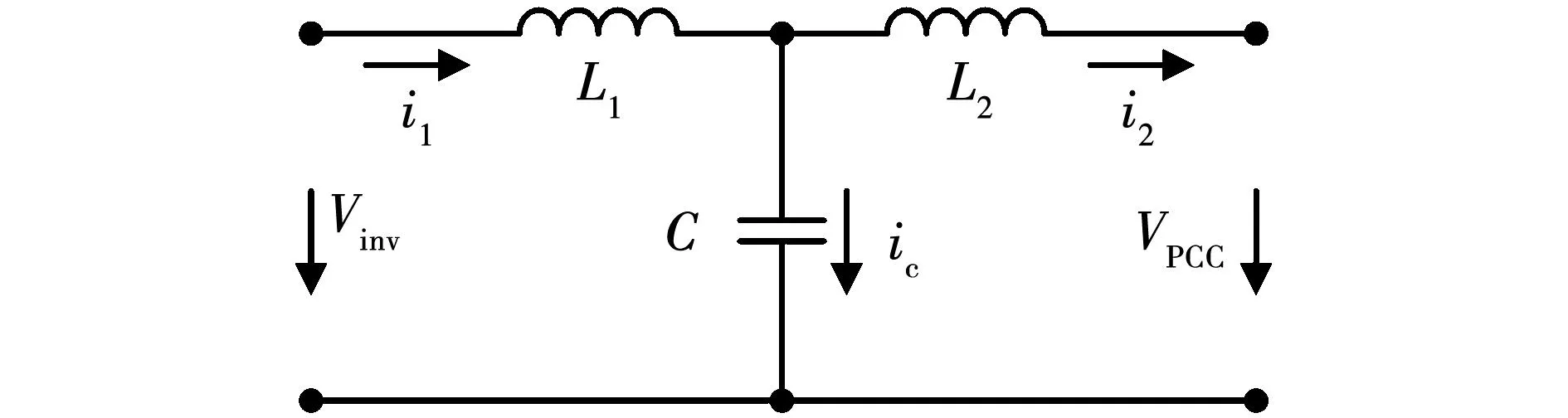
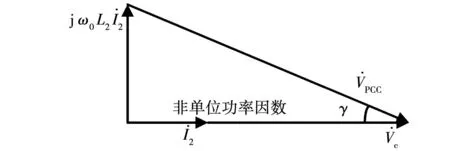
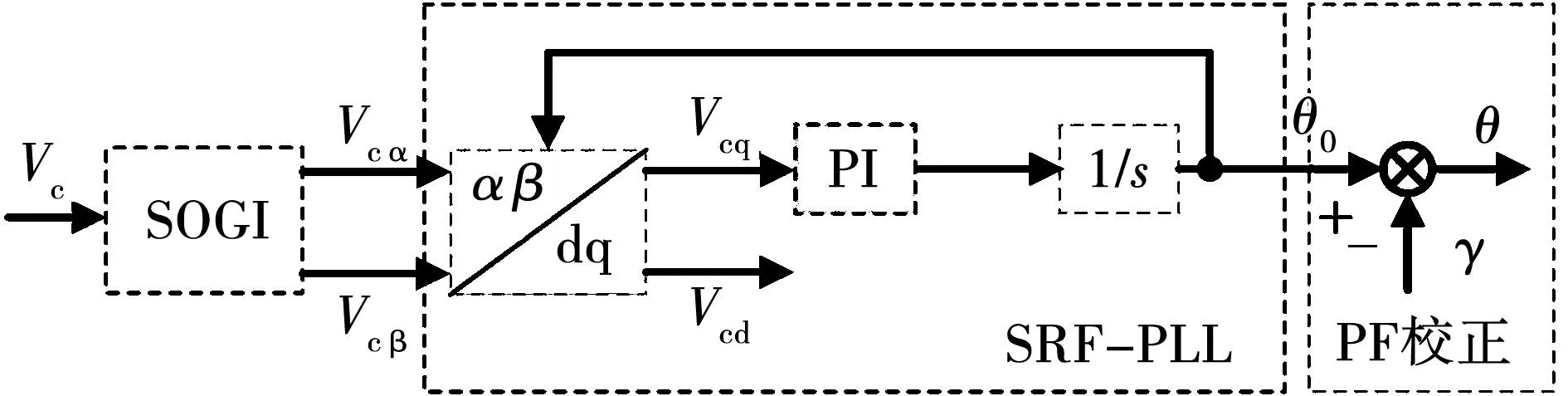
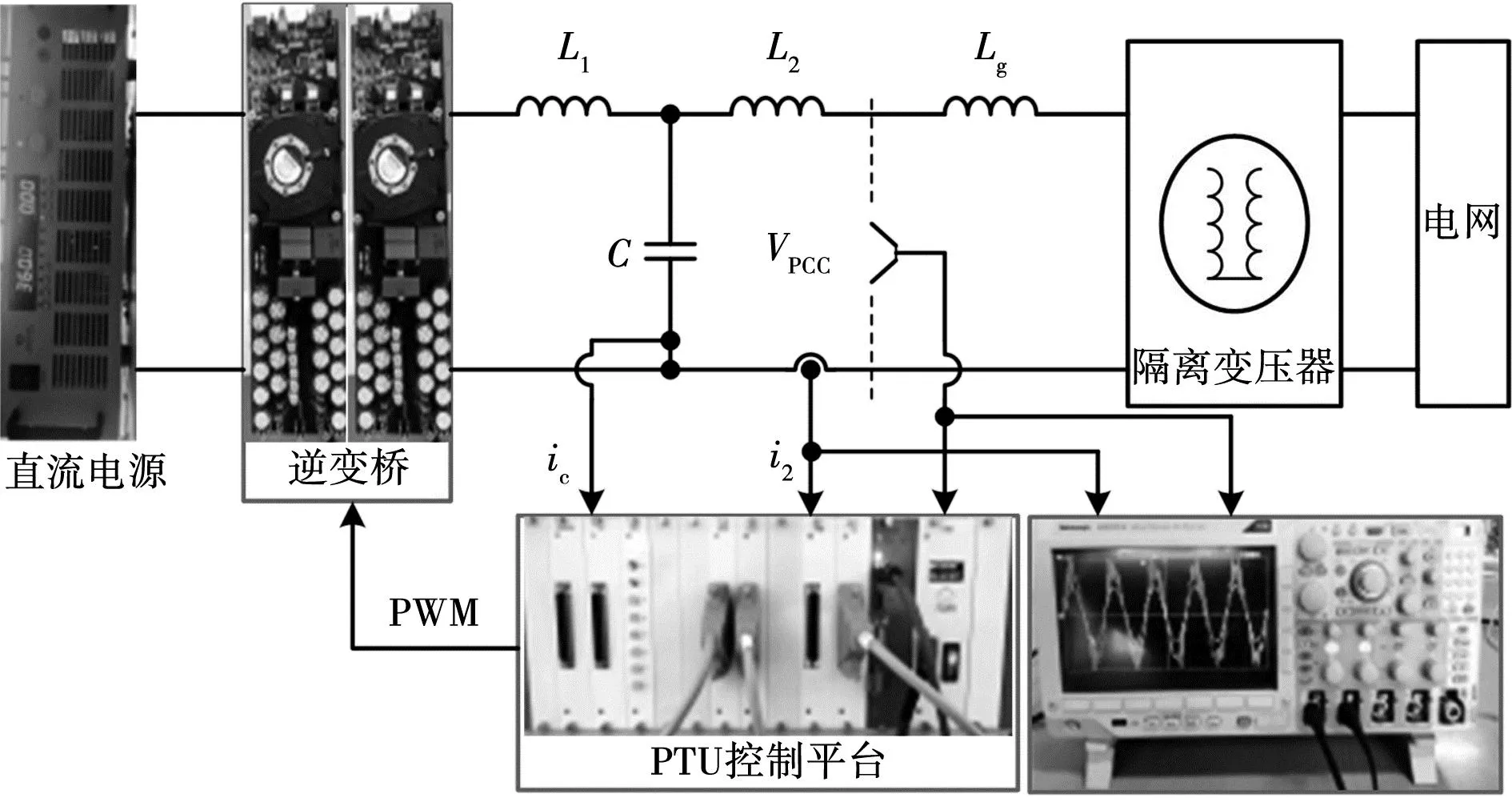
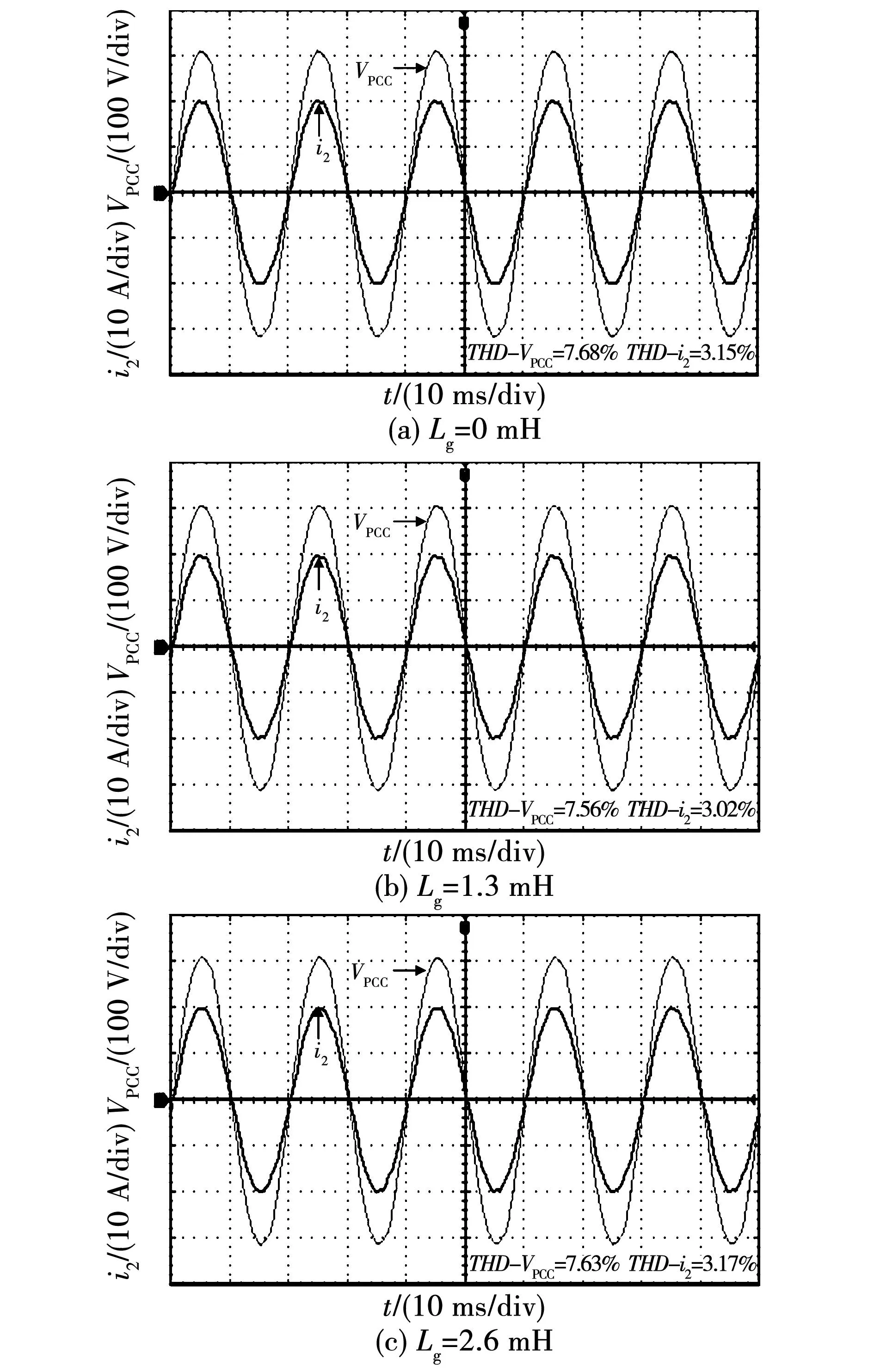
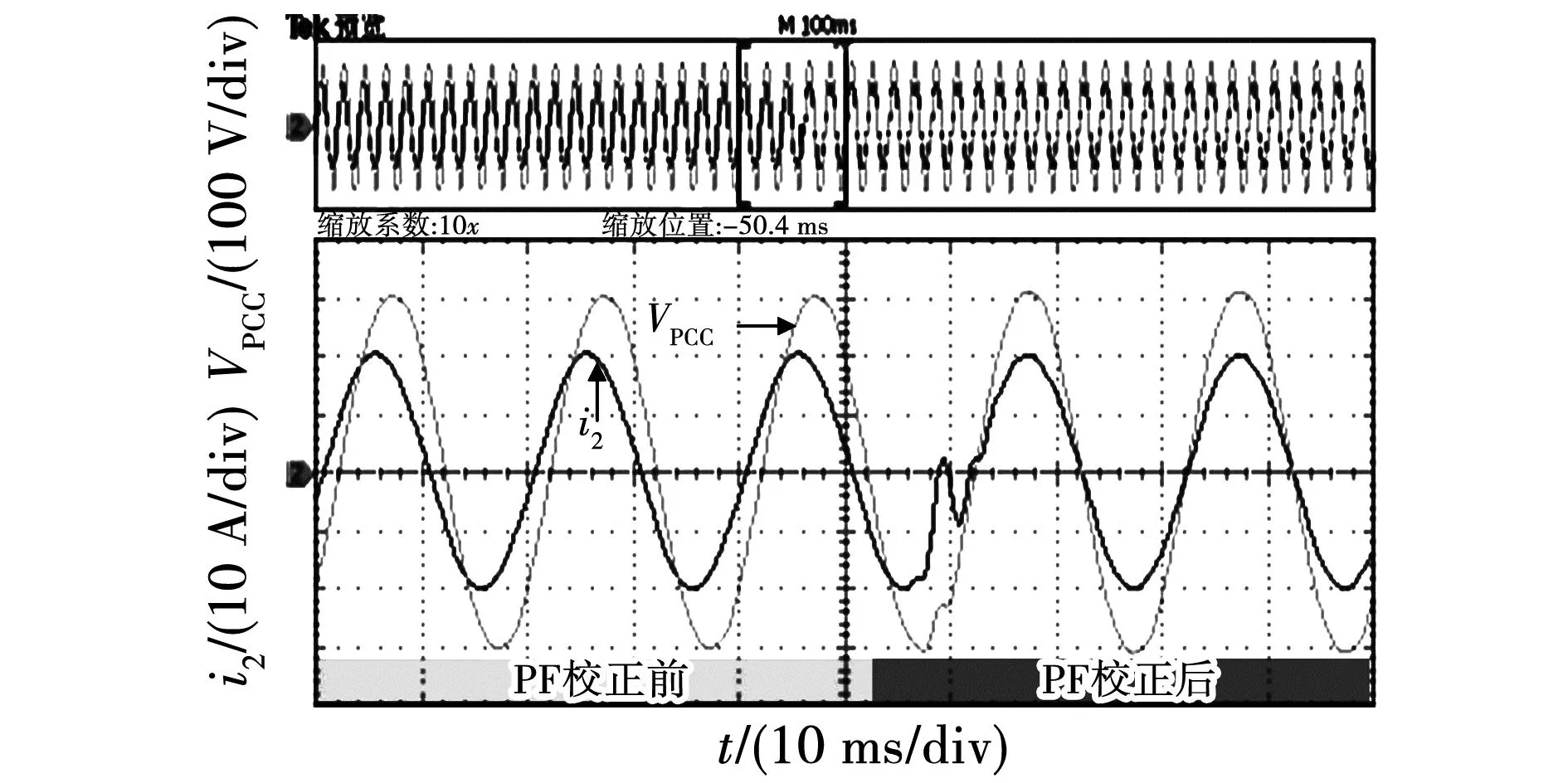
由此可见,当LCL滤波器谐振频率fs/6 实际上,网侧电流包括激励参考电流产生的响应分量,还含有扰动电网电压产生的响应分量,由于参考电流具有较好的正弦度,因此在系统稳定性良好的情况下,使网侧电流发生畸变的主要原因是电网电压的扰动作用。根据图2可以推导出Vg(s)到i2(s)的扰动闭环传递函数Y(s),表达式为 (10) 其中: (11) Gx2(s)= (12) 将s=jω代入式(10),并进行简化可得 |Y(j2πf)|= (13) 其中: (14) 令Lg=Lgm,将式(9)代入式(13),可以得到在频率f=fs/6处有1/|Y(j2πf)|=0成立,意味着当电网阻抗Lg=Lgm时,电网电压在频率fs/6处的背景谐波将得到无限放大,这被称为并网系统的谐波谐振。根据式(13)可以绘制出|Y(j2πf)|关于变量Lg、f的函数图像,如图7所示。观察图7可知,随着Lg的增加,|Y(j2πf)|的谐振尖峰逐渐向fs/6发生偏移,并且谐振程度逐渐加深,电网电压背景谐波将得到放大,此时网侧电流发生严重畸变。 图7 |Y(j2πf)|关于Lg、f的变化曲线 为了验证|Y(j2πf)|对电网电压背景谐波的放大作用,在电网电压Vg中分别注入微量60~80频次谐波电压,其大小为基波幅值的0.25%,并网逆变器在不同电网阻抗条件下的网侧电流仿真波形如图8所示。从图8可以看出,随着Lg的增加,网侧电流质量逐渐劣化,对其进行快速傅里叶变换分析(fast Fourier transform,FFT)可见,谐波含量亦有所增大,并且谐波频次放大现象逐渐向低频域发生偏移,这与前述理论分析吻合。 图8 传统CCFAD方法网侧电流仿真波形 根据第二节分析可知,并网逆变器采用传统电容电流比例有源阻尼方法工作时,随着Lg的增加系统稳定裕度逐渐降低,同时电网电压中的背景谐波将被放大,易引发谐波谐振现象进而劣化并网电能质量。鉴于此,本节提出一种鲁棒性CCFAD方法,可有效提高控制系统在弱电网下的稳定裕度,增强并网逆变器对电网阻抗的适应能力。 图9给出了所提方法的系统结构图,其中H(s)的传递函数表达式为 (15) 图9 鲁棒性CCFAD的系统结构图 式中:K为比例系数;fn代表转折频率。 根据图9,可以得到所提方法的系统开环传递函数T1(s)表达式,为 T1(s)= (16) 将式(5)中的Hi1替换为H(s),即可得鲁棒性CCFAD方法并联在滤波电容支路两端的等效虚拟阻抗Zeq1(s)表达式,为 (17) 同样地,将s=jω代入式(17)得到Zeq1(jω)=Req1(ω)//Xeq1(ω),其等效并联虚拟电阻Req1(ω)与虚拟电抗Xeq1(ω)分别为: (18) 根据式(18)可知,K值与虚拟阻抗Zeq1(jω)的幅值有关,而Req1(ω)和Xeq1(ω)的特性分界频率仅由fn决定。图10给出了Req1(ω)与Xeq1(ω)在奈奎斯特频率(fs/2)范围内关于fn的特性曲线。从图10可以看出,Req1(ω)存在两个分界频率,在频域(0,fR1)、(fR2,fs/2)范围内均表现为负阻特性,而在频域(fR1,fR2)范围内为正阻特性,并且0 图10 Req1(2πf)与Xeq1(2πf)的频率特性曲线 fn=fR1tan(3πTsfR1)≤fr1tan(3πTsfr1)。 (19) 将式(16)改写为 (20) 其中 (21) 根据式(20)可知,ψ(s)等效为前向增益G(s),反馈增益为H(s)的闭环负反馈系统,其开环传递函数为φ(s)=G(s)H(s)。因此,T1(s)不包含右半平面极点与ψ(s)闭环稳定是等价的。将式(17)代入φ(s),得 (22) 由式(22)可见,φ(s)的相位曲线分别在fR1与fR2处各产生一次穿越,记幅值裕度分别为GMR1、GMR2,其伯德图如图11所示。GMR1与GMR2分别表示为: (23) 图11 开环传递函数φ(s)的伯德图 (24) 由于φ(s)不包含右半平面极点,为保证ψ(s)闭环稳定,需满足GMR1>0 dB且GMR2>0 dB。根据式(23)、式(24)可知,GMR1是关于Lg的减函数,而GMR2是关于Lg的增函数,故在Lg变化过程中,仅需满足GMR1>0 dB即可保证ψ(s)闭环稳定,由式(23)可得 (25) 将式(19)代入式(25),得 (26) 如图12阴影部分所示,给出了fR1与K的可取区域。显然,在频域(0,fr1)范围内,K是关于fR1的单调减函数。由于K值会改变虚拟电阻Req1(ω)的幅值大小,势必影响系统谐振尖峰的阻尼效果。因此,为便于设计电流控制器,可适当选取较小的fR1,以此获得较大范围K值,增强系统谐振尖峰的阻尼效果。 图12 fR1与K的可取区域 此外,滤波电容支路为高次谐波提供了低阻抗通路,导致电容电流中含有大量高次谐波电流,为提高脉冲宽度调制的可靠性,可选取分界频率fR1=325 Hz,利用H(s)的低通幅频特性滤除谐波电流,通过(19)可求得fn=50 Hz,此时0 事实上,电网阻抗不可能无穷大,并网逆变器接入电网时,电网强弱可由交流系统短路容量比(short-circuit ratio,SCR)来评定,并网逆变器需要在SCR≥10的复杂工况下稳定运行,因此本文考虑Lg的变化范围为0到2.6 mH(SCR=10)。 由于电网阻抗不利于系统稳定性,如图13所示,给出了T1(s)在Lg=2.6 mH时的伯德图。从图13可以看出,随着K值增加,系统谐振尖峰阻尼效果越来越显著,并且开环截止频率随着K值的增加而提高。因此,为了增强阻尼效果且提高系统带宽,可选取K=898。显然,T1(s)不含右半平面极点,根据奈奎斯特稳定性判据,需使一次负穿越失效,才能够保证并网逆变器控制系统闭环稳定。此时易设计网侧电流反馈系数Hi2=0.044 7,QPR电流控制器的参数为Kp=1、Kr=40[19]。 图13 开环传递函数T1(s)的伯德图 根据前述参数设计,如图14所示,给出了鲁棒性CCFAD方法的开环传递函数T1(s)伯德图。从图14可以看出,当电网电感分别为Lg=0、1.3、2.6 mH时,系统的稳定裕度分别为PM=66°、62.7°、60.1°,GM=8.06、4.75、4.24 dB,此时系统具有较强的稳定性,并网逆变器对弱电网适应能力得到极大地提高。 图14 补偿后T1(s)的伯德图 为避免在Lg变化过程中,系统可能出现局部失稳现象,如图15所示,给出了系统闭环主导极点根轨迹。其中,延时环节采用三阶Pade近似进行线性化处理[20]。 图15 CCFAD方法的主导极点根轨迹 从图15可以看出,随着Lg的增加,传统电容电流比例有源阻尼方法的闭环主导极点逐渐向虚轴靠近,直至出现右半平面极点,并网逆变器失稳;然而,鲁棒性CCFAD方法在Lg变化过程中,系统闭环主导极点始终处于左半平面,系统稳定性得到保证。 同理,将式(7)中的Hi1替换为H(s),如图16所示给出了在所提方法下,|Y(j2πf)|关于变量Lg、f的函数图像。比较图7和图16可以看到,所提鲁棒性CCFAD方法在Lg较宽范围变化时,并网系统对电网电压背景谐波具有极强的抑制作用,并且随着Lg的增加,谐振程度逐渐变弱,避免了谐波谐振现象的发生。由此可见,所提方法不仅提高了并网系统在数字控制延时与电网阻抗交互作用下的稳定性,还增强了电网电压背景谐波抑制效果,有效改善并网电能质量。 图16 所提方法下|Y(j2πf)|关于Lg、f的变化曲线 与图8类似,在电网电压Vg中分别注入微量60~80频次谐波电压,此时谐波大小为基波幅值的0.5%,并网逆变器在不同电网阻抗条件下的网侧电流仿真波形如图17所示。 图17 鲁棒性CCFAD方法网侧电流仿真波形 从图17可以看出,并网逆变器在所提鲁棒性CCFAD方法下运行时,电网电压背景谐波得到抑制,并且随着Lg的增加,网侧电流谐波含量亦逐渐降低,并网系统在适应弱电网能力提升的同时,具有较好的并网电能质量。 LCL型并网逆变器采用传统CCFAD方法及鲁棒性CCFAD方法进行电能变换时,需要使用三组传感器分别采集电容电流ic、网侧电流i2以及并网点电压VPCC的信息。为了降低并网逆变器的硬件成本并增强设备可靠性,所提鲁棒性CCFAD方法可转换为电容电压反馈有源阻尼(capacitive-voltage-feedback-active-damping,CVFAD)控制,系统结构图如图18所示。其中,有源阻尼环节H1(s)=sCH(s)。此时,可通过采集电容电压信息进行锁相,减少了一组电流传感器的使用。然而,并网逆变器将处于非单位功率因数(power factor,PF)并网,为提高电能利用率,需要对并网功率因数进行校正。 图18 鲁棒性CVFAD方法的系统结构图 需要说明的是,逆变器接入电网的并网功率因数测定是在公共并网点进行的,因此在分析并网系统PF时可以忽略电网阻抗的存在。图19为LCL滤波器的电路模型,以网侧电流i2为参考向量,由于采用电容电压Vc锁相,则电容电压与网侧电流同相位。根据基尔霍夫电压定律(Kirchhoff’s voltage law,KVL),如图20给出了Vc和VPCC的矢量关系图。 图19 LCL滤波器电路模型 图20 LCL滤波器矢量关系图 由图20可以求得VPCC与Vc的相位差为 (27) 式中I2和Vc分别代表网侧电流与电容电压的基频有效值,可通过电流、电压传感器采集的信息进行求取。 由此可见,相位差γ是造成逆变器无法单位功率因数并网的原因。为减少并网点处的无功功率,应对功率因数进行校正。如图21所示,给出了传统前置二阶广义积分器(second-order generalized integrator,SOGI)的同步旋转坐标系锁相环(synchronous reference frame PLL,SRF-PLL)原理示意图。显然,根据图20和图21可知,电容电压的相位信息θ0超前并网点电压γ,为保证并网逆变器单位功率因数并网,实际参考电流的相位信息应为θ=θ0-γ,PF校正如图21所示。 图21 锁相环原理示意图 本文采用Rtuit公司开发的实时数字控制器RTU-BOX204控制平台,搭建了如图1所示的3 kW单相LCL型并网逆变器实验样机,主电路参数与表1一致,对所提鲁棒性CCFAD方法进行实验验证,具体实验结构图如图22所示。其中,DCPS8022数字控制直流电源可提供400 V×20 A的输出功率,电流和电压霍尔传感器分别采用ACS712与LV25P,开关管选用两个二单元的IGBT模块2MBI75VA,开关管驱动采用大功率IGBT驱动模块TX-DA962,示波器采用泰克Tektronix MDO3014示波器100 MHz四通道混合域。 图22 单相LCL型并网逆变器实验结构图 为验证所提鲁棒性CCFAD方法的有效性,本节给出相应的实验结果,此时仍采用并网点电压进行锁相。如图23所示,给出了并网逆变器运行在传统电容电流比例反馈有源阻尼控制下的网侧电流i2和并网点电压VPCC的稳态实验波形。可以看出,当电网电感Lg=0.2 mH时,并网逆变器的网侧电流质量已然较差,测得网侧电流总谐波畸变率(total harmonic distortion,THD)的值为4.65%;然而,随着Lg增加至0.3 mH,此时开环系统稳定裕度较低,电网电压中含有的背景谐波得到相应的放大,网侧电流与并网点电压波形发生明显畸变,并网电能质量较差,此时网侧电流与并网点电压的THD值分别达到了62.35%和20.83%,无法满足相应的并网要求(网侧电流THD<5%)。这与前述理论分析相吻合。 图23 传统CCFAD方法下的并网实验波形 当并网逆变器在所提鲁棒性CCFAD方法下运行时,网侧电流i2和并网点电压VPCC的稳态实验波形如图24所示。显然,并网系统分别在Lg=0、1.3、2.6 mH条件下均具有良好的入网电能质量,测得的相应网侧电流THD值均小于4%,验证了所提方法可显著提高并网逆变器对弱电网的适应能力,系统鲁棒性得到增强。此外,图25给出了网侧电流跳变的动态实验波形。从图25可以看出,当设置参考电流进行满载/半载动态跳变的情况时,网侧电流在跳变瞬间出现短暂的调节过程,但很快进入稳态,系统具有良好的动态性能。 图24 鲁棒性CCFAD方法下的并网实验波形(VPCC锁相) 为验证所提方法的灵活性,本节给出了鲁棒性CVFAD方法相应的实验结果,此时仍采用并网点电压进行锁相。分别设置电网电感Lg=0、1.3、2.6 mH,当并网逆变器采用鲁棒性CVFAD进行并网运行时,其网侧电流i2和并网点电压VPCC的稳态实验波形如图26所示。 图26 鲁棒性CVFAD方法下的并网实验波形 (VPCC锁相) 从图26可以看出,并网逆变器运行在CVFAD方法下的入网电能质量较好,可适应弱电网下较宽范围变化的电网阻抗,系统具有较强的鲁棒性。 为了减少一组电流传感器的使用,可采集电容电压信息进行锁相,此时并网逆变的网侧电流和并网点电压实验结果如图27所示。结合图20可知,网侧电流i2超前VPCC的角度为γ,从图27可以看出,采用电容电压锁相将造成并网逆变器无法单位功率因数并网,此时需对其进行功率因数校正。如图28所示,给出了并网逆变器在Lg=0 mH时进行PF校正后的并网实验波形。从图28可以看出,PF校正前i2超前VPCC的角度为γ,切换为PF校正时网侧电流出现短暂的动态跳变过程即可恢复稳态,并且此时并网逆变器实现单位功率因数并网。 图27 鲁棒性CVFAD方法下的并网实验波形(Vc锁相) 图28 功率因数校正后的并网实验波形(Vc锁相) 由此可见,相较于传统CCFAD方法,本文所提鲁棒性CCFAD方法可有效改善并网系统在数字控制延时与电网阻抗交互影响下的稳定性,其良好的入网电能质量满足并网要求。此外,CVFAD方法的应用,在引入PF校正环节后,不仅节省了一组电流传感器的使用,还可以保证并网逆变器的单位功率因数并网,极大地提高了电能利用率。 本文以单相LCL型并网逆变器为例,对采用CCFAD方法在弱电网条件下进行并网运行时的空控制系统稳定性进行分析,得出以下结论: 1)通过对传统CCFAD方法进行分析,明确了数字控制延时与电网阻抗交互作用对并网逆变器控制系统稳定性造成的影响:数字控制延时导致并联等效虚拟电阻在一定频域范围内表现出负阻特性,造成并网逆变器无法适应较宽范围变化的电网阻抗,易引发谐波谐振现象,甚至失稳离网。 2)针对数字控制延时导致的失稳问题,本文提出一种利用负一阶惯性环节进行电容电流反馈有源阻尼控制的鲁棒性CCFAD方法,该方法可保证并联等效虚拟电阻在滤波器谐振频率有效范围内始终表现为正阻特性,极大地提高了并网逆变器对电网阻抗的鲁棒性,稳定提升的同时,并网系统谐波谐振亦得到抑制。 3)进一步对所提鲁棒性CCFAD方法进行改进,可通过采集电容电压状态变量进行反馈控制,对谐振尖峰进行有源阻尼,得到鲁棒性CVFAD方法。此外,当利用电容电压进行锁相获得网侧参考电流相位信息时,并对其进行功率因数校正,相较于传统CCFAD方法和鲁棒性CCFAD方法,节省了一组电流传感器的使用,降低设备成本。1.2 并网系统的谐波谐振分析
2 鲁棒性CCFAD方法
2.1 鲁棒性CCFAD的等效虚拟阻抗
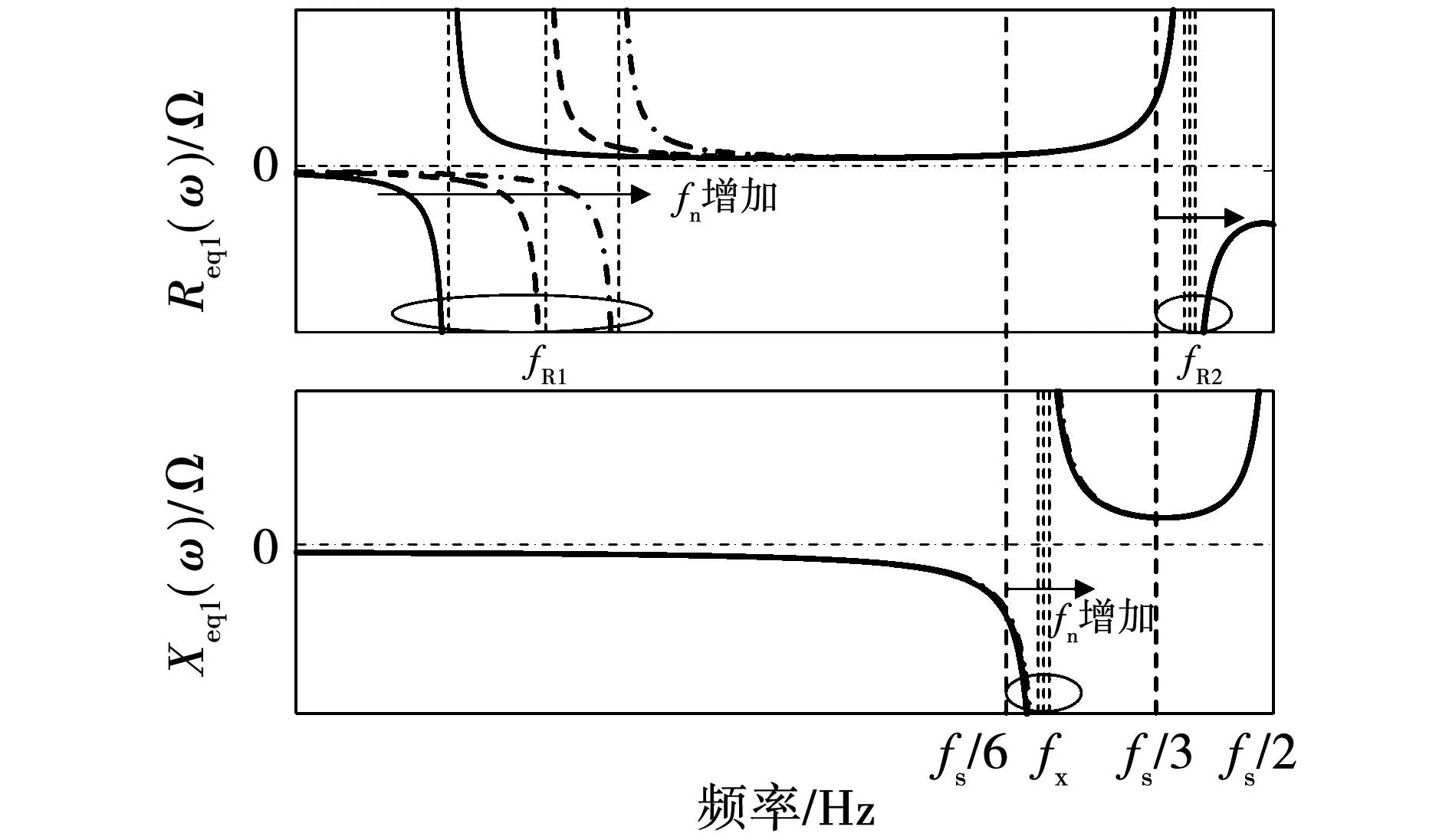
2.2 参数设计
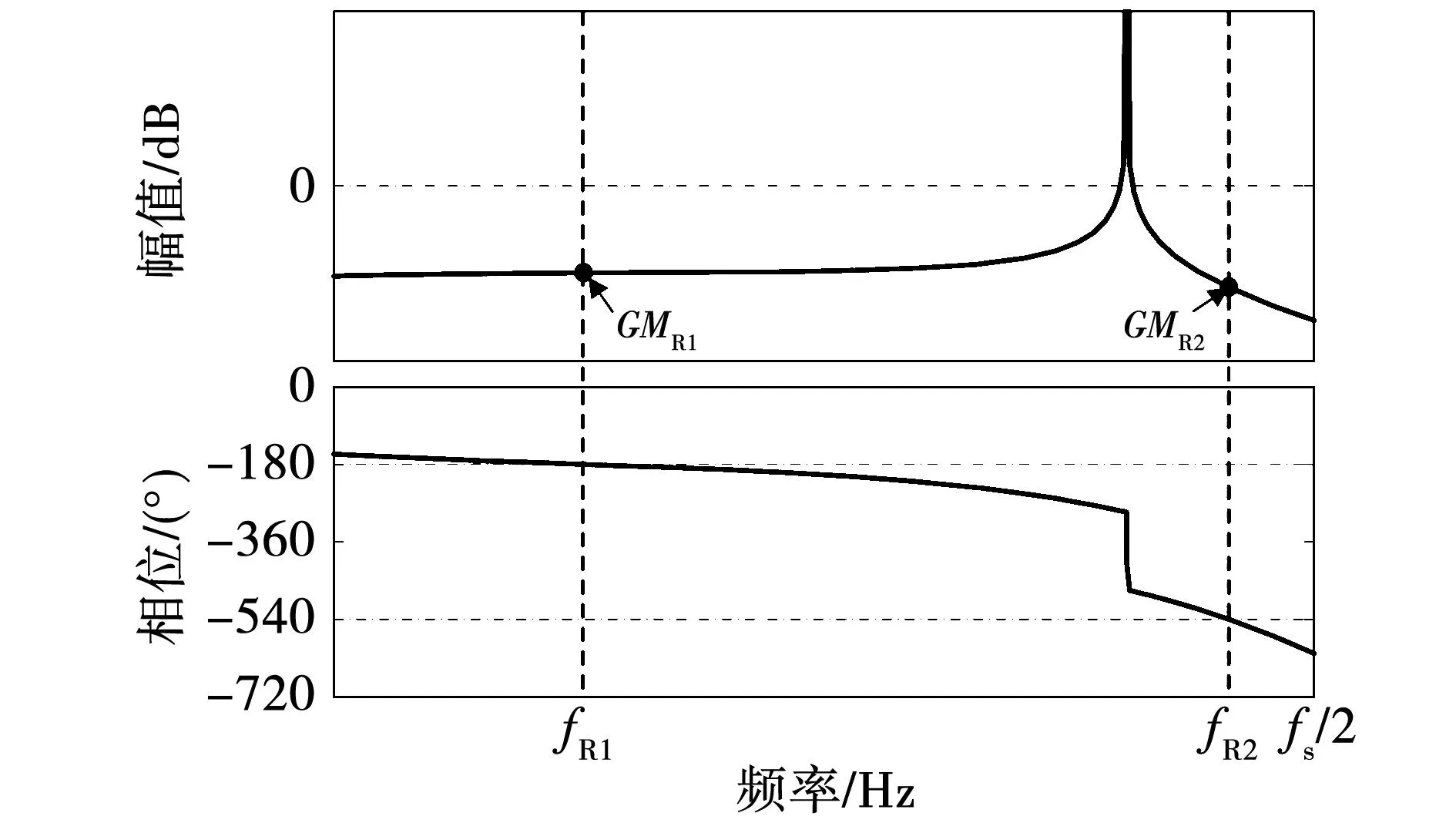
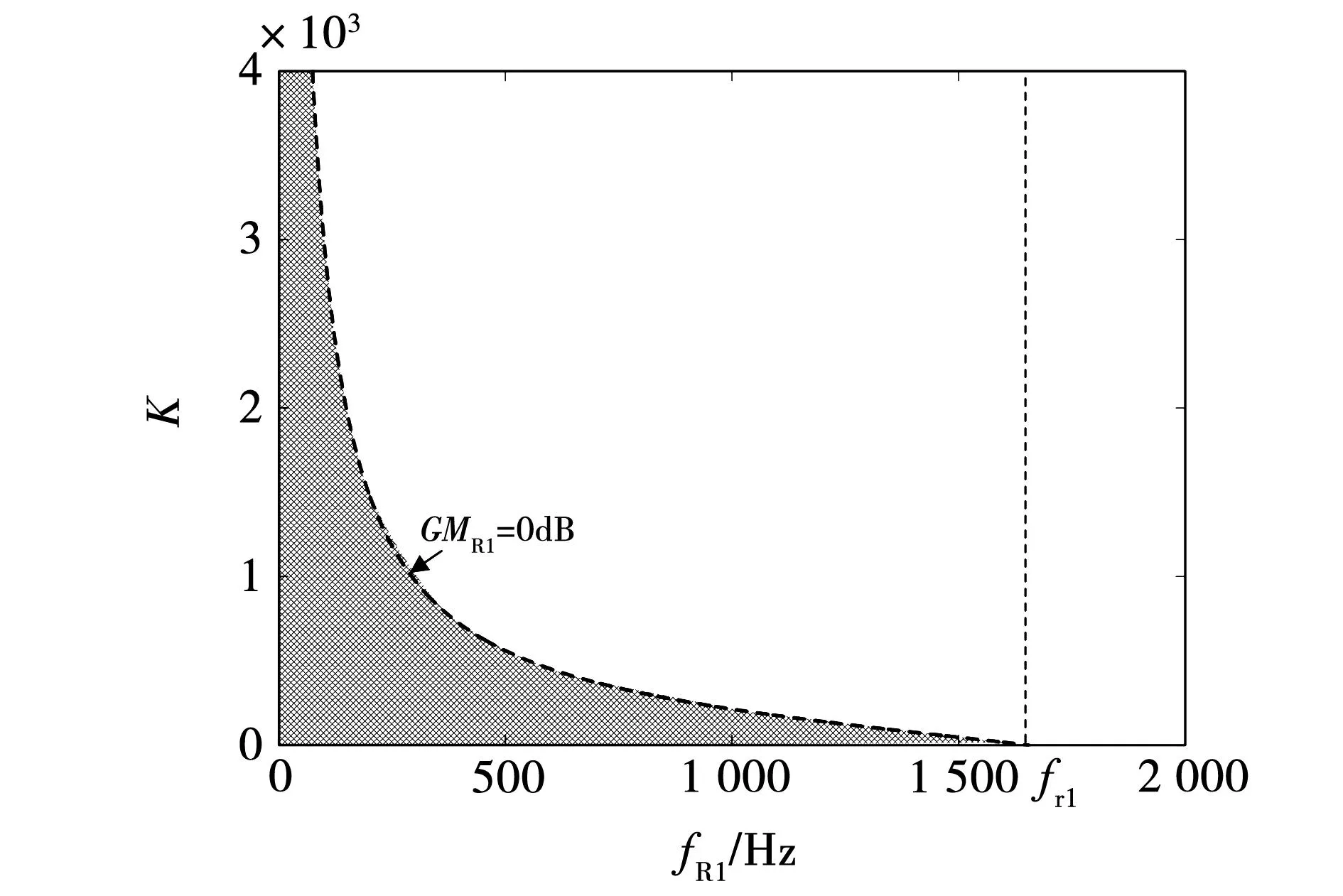
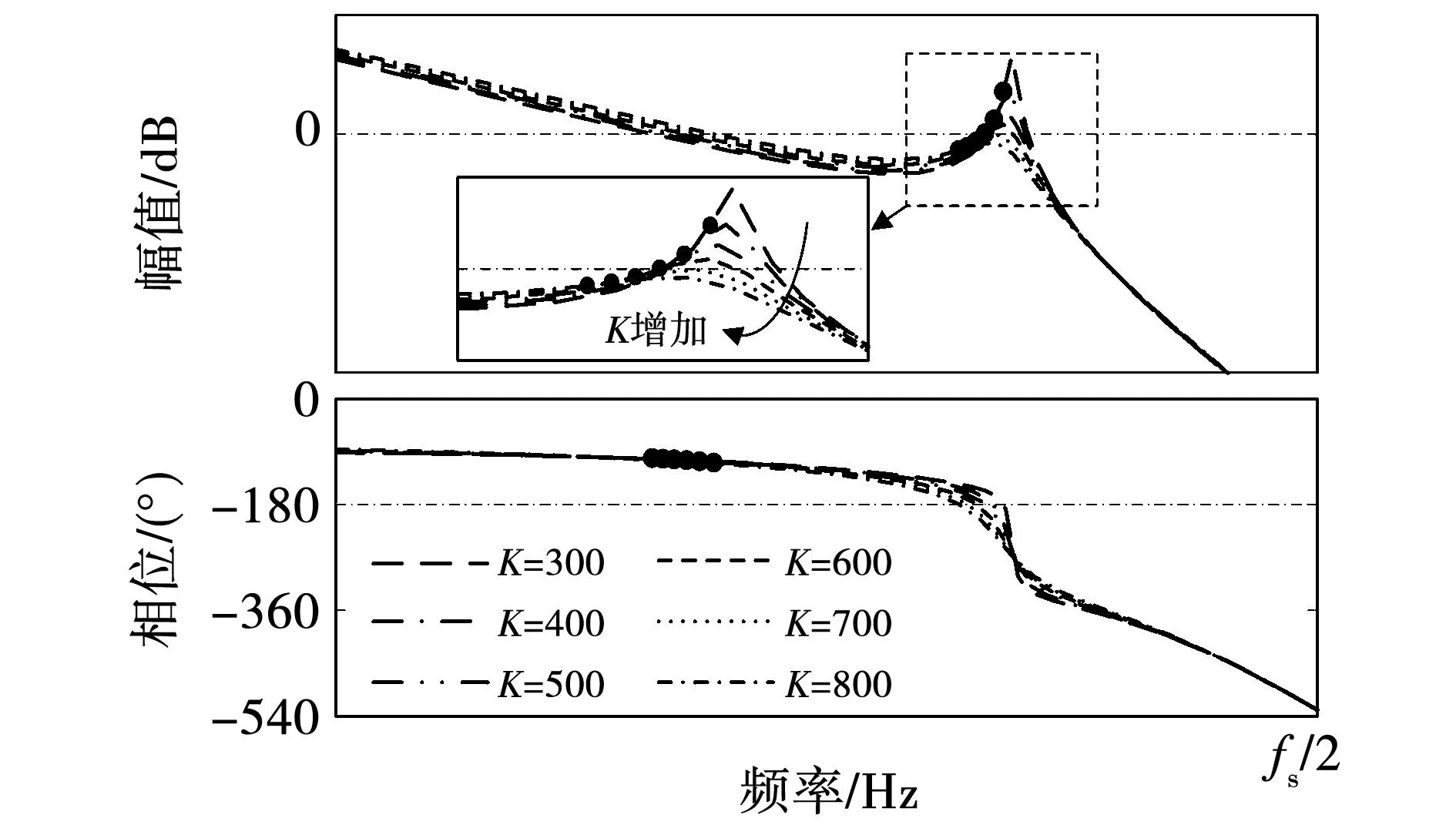

2.3 鲁棒性CVFAD方法及其PF校正
3 实验验证
3.1 鲁棒性CCFAD方法的实验结果


3.2 鲁棒性CVFAD方法的实验结果

4 结 论

