永磁/磁阻混合转子双定子低速大转矩同步电机冷却及热管理技术研究

张兆宇, 于思洋, 张岳, 金石, 戚子豪, 张凤阁

(1.沈阳工业大学 电气工程学院,辽宁 沈阳 110870; 2.山东大学 电气工程学院,山东 济南 250061)

0 引 言

低速大转矩传动系统在工业生产、油田开采等领域有极其重要的应用[1]。低速大转矩传动装备多采用“常规转速电机+减速齿轮机构”的驱动方式,这不仅使驱动系统体积增大、维护成本增加、系统可靠性和运行效率降低,而且增加了系统加工制造、运输装配等方面的难度,因此当前低速大转矩传动系统正在向着直驱化方向发展[2]。永磁同步电动机具有结构简单、效率和功率因数高、起动转矩大、经济运行范围宽等优点,特别适合应用于低速大转矩直驱系统[3-6]。然而,常规低速大转矩永磁同步电机体积较大,其内部空间未得到有效利用,转矩密度较低[7-9]。针对这一问题,本文提出一种具有高转矩密度的永磁/磁阻混合转子双定子低速大转矩同步电机,为保证该电机的可靠运行,有必要对其温度分布进行准确计算并设计有效的冷却系统。

文献[10]针对永磁同步电机设计了一种集中参数热网络模型,该网络可有效模拟电机定子轭、定子绕组、定子齿和永磁体四个重要部分。文献[11]分别提出一种新型瞬态三维集中参数热模型和三维有限元热模型用以预测永磁辅助同步磁阻电机在不同故障条件下的非对称温度分布。文献[12]针对非晶合金永磁电机温度场的计算,提出一种改进型有限公式迭代算法,该方法简化了循环计算中对导热系数的修正计算过程,降低了迭代计算量。文献[13]建立了一种用于计算永磁电机瞬态温度场的等效热网络模型,并分析了影响瞬态热网络计算准确性的影响因素。文献[14]提出一种新型永磁同步电机水冷系统,该冷却系统通过在电机铁心中添加水冷板以达到更为理想的冷却效果。文献[15]研究了散热风刺不同尺寸对低速大转矩永磁电机转子散热效果的影响规律,探讨了转子轴向和径向通风道对降低永磁体温升的有效性。文献[16]针对航空永磁电机提出一种风冷与热管相复合的新型冷却系统,并对其冷却性能开展了相关研究工作。

综上可知,国内外专家学者对永磁电机的温升计算方法与冷却系统设计开展了大量研究工作。然而,本文所研究的电机结构特殊,温度场分布不规律,温度计算与常规电机有较大不同,冷却系统难以设计。为此,本文建立特殊结构电机整机结构的热网络温度计算模型,推导电机结构零件之间热阻计算数学模型,根据电机温度计算结果,设计一种针对该电机双定子结构的外水道内水管的双水冷冷却系统,研究分析冷却系统设计参数对冷却效果的影响,并通过仿真与实验手段验证所提电机温度计算方法的准确性和冷却系统的有效性。

1 电机总体结构

为避免电机发生扫膛现象,本文设计了一种适用于混合转子双定子低速大转矩同步电机的双端支撑拓扑结构,如图1(a)所示。混合转子双定子低速大转矩同步电机由内、外定子及永磁/磁阻混合转子组成。其中:永磁体与外定子组成外单元电机;磁障转子与内定子组成内单元电机;在永磁体与磁障之间添加隔磁环,既使永磁体与磁障形成统一整体,又使两者之间的磁路彼此独立,方便电机的设计与控制。电机总体机械结构如图1(b)所示,其中为了方便内定子绕组出线,提出一种空心静止轴结构,即图1(a)中的非驱动轴采用空心结构。电机主要尺寸如表1所示。

图1 电机拓扑结构及机械结构示意图

2 等效热网络模型的建立

2.1 等效热网络模型

混合转子双定子低速大转矩同步电机结构特殊且复杂,其温度场计算方法与传统电机有很大不同。为此,本文建立了该电机精确热网络计算模型,推导了考虑永磁/磁阻混合转子及空心静止轴等特殊结构之间热传导的热阻数学模型,并以此为基础对电机各部分稳态温度进行计算。

为简化计算,做如下假设:1)电机温度沿圆周对称分布,同一圆周面上的冷却条件相同;2)腔内空气各点的温度相同,即用同一节点进行划分;3)忽略集肤效应对定子绕组的影响;4)忽略磁障转子各导磁层间连接筋的影响。基于上述假设,将电机模型划分为多个正交的网络拓扑结构,并将这些网格单元中心定义为所求温度的节点,得到如图2所示的电机等效热网络节点分布图,图中“◎”代表热源,“⊥”代表对流传热,“—”代表热传导。

图2 等效热网络节点分布图

2.2 热阻数学模型分析与计算

本文主要针对结构特殊的永磁/磁阻混合转子与空心静止轴的热网络模型进行详细分析。

2.2.1 永磁体热阻(以永磁体节点17为例)

永磁体节点17分别与齿节点14、永磁体节点18、转子轭节点20、腔内空气节点70进行换热。

1)节点17与齿节点14之间热阻可表示为

(1)

式中S1417和αg分别代表导热面积和气隙散热系数,可分别通过下式进行求解:

(2)

(3)

式中:bt1、L和Z1分别代表外定子齿宽、电机轴向长度和外定子槽数;λair代表空气导热系数;Nu代表空气努塞尔特系数,其取值取决于若特洛系尔数Ta的大小。若Ta>41.2(气隙中流体处于紊流状态),则Nu=0.42Ta0.5Pr0.25,Pr代表空气普朗特系数;若Ta<41.2(气隙中流体处于层流状态),则Nu=2。其中,Ta可表示为

(4)

式中:rm=(r1+r2)/2,r1和r2分别代表外定子内径和转子外径;g为气隙长度;ω为转子角速度;v为空气粘度。

2)节点17与节点18之间热阻可表示为

(5)

式中:λPM为永磁体导热系数;S1718代表永磁体横截面积。

3)节点17与节点20间热阻可表示为

(6)

式中:hPM为永磁体厚度;hr为转子轭厚度;λDW1为硅钢片径向导热系数;S1720代表永磁体与转子轭接触面积。

4)节点17与节点70之间热阻可表示为

(7)

式中:S1770代表永磁体与空气接触面积;α1770代表永磁体与气腔之间的散热系数,表达式为:

(8)

(9)

(10)

式中:Dy代表永磁体外径;Rer为端面雷诺数;γ代表空气动力粘度系数;n为电机转速。

2.2.2 转子轭热阻(以转子轭部节点20为例)

转子轭节点20分别与永磁体节点17、轴向转子轭节点21、隔磁环节点24、腔内空气节点70进行换热。

1)节点20与节点17之间热阻和节点17与节点20之间热阻相同,即R2017=R1720。

2)节点20与节点21之间热阻可表示为

(11)

式中:λDW2为硅钢片轴向导热系数;S2021为导热面积,可表示为

(12)

其中Dr1和Dr2分别表示转子轭的外径和内径。

3)节点20与节点24之间热阻可表示为

(13)

式中:S2024代表转子轭与隔磁环之间导热面积;λAl代表铝导热系数;hg为隔磁环厚度。

4)节点20与节点70之间热阻可表示为

(14)

式中:S2070代表转子轭与空气接触面积;α2070代表转子轭端面散热系数,其计算与α1770相似。

2.2.3 隔磁环热阻(以隔磁环节点23和节点24为例)

隔磁环节点23分别与隔磁环节点24、腔内空气节点70、转子前端盖节点54进行换热。

1)节点23与节点24之间热阻可表示为

(15)

式中:S2324=S2425;L2324代表节点23与节点24之间热传导距离,可表示为

(16)

其中Lgch为隔磁环长度。

2)节点23与节点70之间热阻可表示为

(17)

式中:α2370u和α2370d为隔磁环两侧对流散热系数;S2370u与S2370d分别为节点23与两侧空气之间的接触面积,可分别表示为:

(18)

(19)

3)节点23与节点54之间热阻可表示为

(20)

式中:hzg为转子前端盖厚度;λzg为转子前端盖导热系数;S2354代表导热面积。

隔磁环节点24分别与转子铁心节点20、轴向隔磁环节点23、25和第一导磁层节点28进行换热。

1)节点24与节点20之间热阻和节点20与节点24之间热阻相同,即R2420=R2024。

2)节点24与节点23之间热阻和节点23与节点24之间热阻相同,即R2423=R2324。

3)节点24与节点25之间热阻可表示为

(21)

式中S2425代表导热面积,可表示为

(22)

其中Dg1和Dg2分别表示隔磁环外径和内径。

4)节点24与节点28之间热阻可表示为

(23)

式中:hc1为第一导磁层厚度;S2428代表第一导磁层与隔磁环之间导热面积。

2.2.4 转子磁障热阻(以转子磁障节点28为例)

转子磁障节点28分别与隔磁环节点24、轴向导磁层节点29、第二导磁层节点31、内定子齿节点37、腔内空气节点70进行换热。

1)节点28与节点24之间热阻与节点24与节点28之间热阻相同,即R2824=R2428。

2)节点28与节点29之间热阻可表示为

(24)

式中S2829为导热面积。

3)节点28与节点31之间热阻可表示为

(25)

式中:S28311与S28312分别为第一导磁层面积和第二导磁层的导热面积;e1,e2分别为第一导磁层和第二导磁层的厚度。

4)节点28与节点37之间热阻可表示为

(26)

式中S2837代表磁障转子第一导磁层与内定子之间导热面积。

5)节点28与节点70之间热阻可表示为

(27)

式中:α2870代表磁障转子端面与气腔散热系数;S2870代表磁障转子端面与气腔散热面积。

2.2.5 空心静止轴热阻(以空心静止轴节点49和52为例)

空心静止轴节点49分别与内定子轭节点45、轴向静止轴节点48和50进行换热。

1)节点49与节点45之间热阻可表示为

(28)

式中:hy2代表内定子轭厚度;S49451代表内定子轭导热面积;S49452代表静止轴导热面积;Dj1和Dj2分别代表静止轴外径和内径;λs代表轴导热系数;L4945代表装配间隙,可表示为

L4945=(0.5+3Dj1)×10-5。

(29)

2)节点49与节点48之间热阻可表示为

(30)

式中:L4948代表节点49与节点48之间热传导距离;S4948代表空心静止轴轴向导热面积。

3)节点49与节点50之间热阻可表示为

(31)

式中S4950代表空心静止轴轴向导热面积,有S4950=S4948。

空心静止轴节点52分别与机壳后端盖节点60、轴向静止轴节点51和53进行换热。

1)节点52与节点60之间热阻可表示为

(32)

式中:L5260代表装配间隙;Dt代表机壳后端盖圆筒外径;λhdg代表机壳后端盖导热系数;S5260代表空心静止轴与机壳后端盖之间导热面积。

2)节点52与节点51和53之间的热阻为空心静止轴同层轴向热阻,计算方法与节点49与节点48和50的计算方法相同,不再赘述。

根据热阻计算公式,计算出各个节点热阻,并将热阻转化为热导,列写出各节点的热平衡方程,将其写成矩阵形式,即

GT=W。

(33)

式中:G表示热导矩阵;T表示温度矩阵;W表示热源矩阵,热源来自于各节点所分配的损耗。

基于电机等效热网络模型和热阻数学模型,编写了电机稳态温度计算程序,得到了自然冷却条件下电机各节点温度平均值,如表2所示。

表2 各节点平均温度

2.3 有限元验证

为验证所建立的等效热网络模型的正确性与有效性,采用有限元方法对电机在自然冷却条件下的温度场进行仿真计算。电机主要结构的温度场仿真结果如图3所示,有限元仿真与热网络数值计算所得的电机各部分温度结果如表3所示。

表3 有限元仿真与热网络数值计算结果

图3 混合转子双定子低速大转矩同步电机温度分布

由结果可知,两种方法所得电机温度分布特点相同,即电机温度沿轴向呈对称分布,外单元电机定子绕组端部温度最高,而内单元电机定子中间部分温度最高,这与内外单元电机结构和自然冷却的散热方式有关。此外,热网络法数值计算结果与有限元仿真结果接近,误差较小,这很好地证明了本文所建立的热网络模型的正确性与有效性。

3 冷却系统设计及效果分析

考虑电机温度分布特点及加工装配等问题,本文设计了一套双水冷方案的冷却系统。

3.1 外电机水冷却系统设计

按照水流的流动方式,水冷系统结构主要可以分为轴向型、螺旋形和周向型,如图4所示。对比水路结构可知:轴向水路可以将进出口设置在一侧,结构简单、易于制造,但水路拐角较多,水流阻力较大,进出水口温度差较大,易造成三相绕组温度不一致;周向水路中冷却水沿圆周方向流动,经过一段轴向距离后沿圆周折返,从入水口循环流动至出水口,尽管周向水路相比于轴向水路折返次数减少,但同样存在拐角问题;螺旋型水路进出水口设置在两侧,冷却水沿圆周方向层层流动,水道相对平滑,阻力较小。鉴于常用水路结构的优缺点,本文采用螺旋水道形式对外单元电机进行冷却。

图4 常见水路结构

在水流速为0.5 m/s,散热面积基本一致的条件下,研究电机额定运行时水道数量对外单元电机冷却效果的影响及水道数量与流阻之间的关系,结果分别如图5和图6所示,其中水道数量与水道截面参数之间的关系如表4所示。

表4 电机额定参数

图5 水道数量对外单元电机冷却效果的影响

图6 水道数量与流阻之间关系

由图5和图6可以看出,在水流速相同以及散热面积基本一致的条件下,水道数量对外电机冷却效果影响不显著,但水道数量对流阻具有较大影响,水道数量越多,流阻越大。因此,综合考虑散热效果及流阻与水泵耗能关系等因素,在对外单元电机冷却系统进行设计时,机壳的冷却水道数量不宜过多。

图7和图8分别给出水道数量为4,水道截面长度为50 mm,水道截面宽度为10 mm条件下,电机额定运行时,冷却水流速对外单元电机冷却效果的影响以及水流速与流阻之间的关系。

图7 水流速对外单元电机冷却效果的影响

图8 水流速与流阻之间的关系

由图7和图8结果可知,冷却水初始流速对电机冷却效果影响较大,随着冷却水流速增加,电机温度逐渐降低,当冷却水流速在0～0.5 m/s之间,温度变化显著,当水流速大于0.5 m/s后,随着水流速的增加,温度下降变缓。此外,随着水流速的增加,流阻也逐渐增大。因此,在选择螺旋水道对电机进行冷却时,应合理选择进水口水速。

3.2 内电机水冷却系统设计

相比于外单元电机,内单元电机散热困难,温升较高,且无法铺设冷却水道,为此本文提出在内定子铁心中插入冷却水管的方式对其进行冷却,冷却水管通过空心静止轴内腔引出,如图9所示。

图9 内单元电机水冷结构示意图

在水管直径为12 mm且电机额定运行条件下,研究冷却水管单管数量分别为16、20、24三种情况对内单元电机冷却效果及管道流阻的影响,其结果分别如图10和图11所示。由图可知,水管数量越多,冷却效果越好,但流阻越大。此外,考虑到该冷却方式为在内电机定子铁心中直接插入冷却水管,水管数量会对内单元电机的磁路产生影响,水管数量越多,越易使内单元电机磁路饱和,影响电机的运行效果,因此水管数量的选择要适中,不宜过多。

图10 水冷管数量对内单元电机冷却效果的影响

在冷却水管数量为16且电机额定运行条件下,研究水管直径分别为10、12、14 mm 3种情况对内单元电机冷却效果及管道流阻的影响,其结果分别如图12和图13所示。

图12 冷却水管截面积对内单元电机冷却效果的影响

图13 冷却水管截面积与流阻之间的关系

由图12可知,在冷却水管数量一定的条件下,水管截面积越大,冷却效果越好。由图13可知,在相同的进水口流速下,冷却水管截面积越小,流阻越大。尽管水管截面积越大对电机的冷却效果越好,但在选择冷却水管截面积时同样要考虑其对电机磁路的影响,水管截面积过大会使内定子铁心容易发生磁路饱和,影响其运行性能。

3.3 基于双水冷系统的热计算

根据上述分析,选择外电机机壳水道结构为螺旋型结构,螺旋型水道数量为4,冷却水流速为0.8 m/s;内电机单根冷却水管数量为16,水管直径为12 mm,冷却水流速为1 m/s。在冷却系统作用下,电机额定运行时的温度分布结果如图14所示。

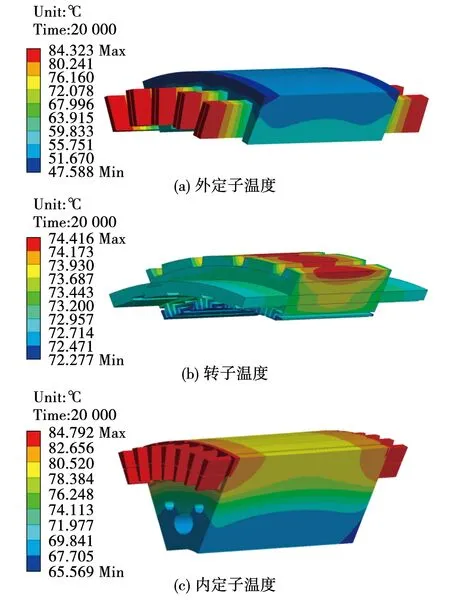
图14 双水冷方式下电机温度分布

由图14结果可知,外单元电机定子最高温度由137.0 ℃下降到了84.3 ℃,且最高温度出现在外定子绕组端部,混合转子最高温度由193.1 ℃降低到了74.4 ℃,内单元电机定子最高温度由193.4 ℃降低到了84.8 ℃,且最高温度同样出现在内定子绕组端部。电机各部分温度明显降低,确保了电机各部件的温升都在允许范围内,冷却效果良好,证明了所提出的冷却系统的合理性与有效性。此外,对比图3可知,由于内单元电机的冷却是在内定子铁心中插入冷却水管,因此其可有效降低内定子铁心温度,从而使得内单元电机在冷却系统作用下,最高温度出现在定子绕组端部,这也很好地证明了针对内单元电机所设计冷却系统的有效性。

4 实验验证

为有效验证本文针对永磁/磁阻混合转子双定子低速大转矩同步电机所建立等效热网络计算模型的准确性以及所设计冷却系统的有效性,搭建了该种电机的温度测试实验平台,如图15所示。其中实验样机的额定数据如表5所示。

表5 电机额定参数

图15 实验样机测试平台

图16给出了内外冷去水流速均为1 m/s,外水道数量为4,水道截面宽度为10 mm,内水管数量为16,水管直径为12 mm,电机输出额定功率时的温度实验测试结果。由结果可知,内单元电机定子绕组端部稳态温度为79.5 ℃,外单元电机定子绕组端部稳态温度为73.6 ℃。由于实验时外水冷系统的水流速高于仿真所设置的水流速,且实验环境温度低于仿真设置温度,因此电机实验冷却结果优于仿真结果。实验结果充分证明了本文所设计冷却系统的有效性和可行性。

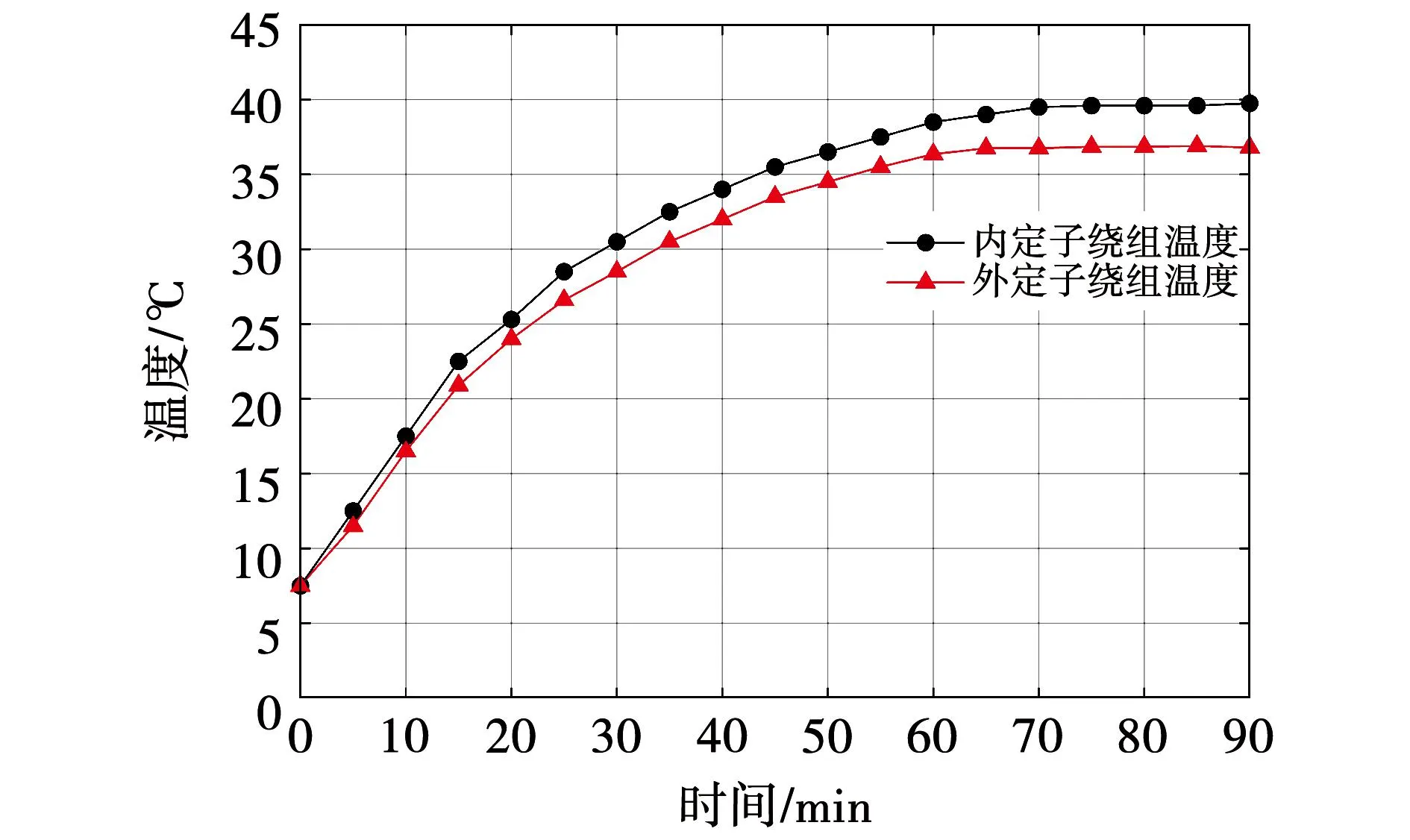
图16 样机温度测试曲线

5 结 论

本文针对永磁/磁阻混合转子双定子低速大转矩同步电机的温度场精确计算及冷却系统设计问题开展相关研究工作。建立该新型电机精确热网络温度计算模型,推导了包括混合转子和空心静止轴等特殊结构件在内的电机各结构件的热阻解析数学模型,在此基础上计算了电机额定运行时的各节点稳态温度,并将解析计算结果与有限元仿真结果进行对比分析,两者计算结果的误差较小,所反映出的电机温度分布规律相同。基于电机温度计算结果,设计了一种针对该电机特殊结构的双水冷冷却系统,采用解析与有限元相结合的方式研究分析了水道形状、水道数量、水管数量、水管截面积等内外水冷系统结构参数对冷却效果的影响,进而总结了该种电机冷却系统的设计原则,并通过有限元仿真与实验测试的方法验证了本文所设计冷却系统的有效性。