基于哈里斯鹰优化算法的光伏储能容量配置优化

丁 伟，苏新凯，廖圣瑄，唐起超，杨继盛

（1.龙源（北京）风电工程设计咨询有限公司，北京 100034；2.国家能源集团新能源技术研究院有限公司，北京 102209；3.龙源（青海）新能源开发有限公司，青海 格尔木 816099）

为缓解光伏发电波动大的现象，各省纷纷提出新能源需配置储能[1-3]要求，目前国内的储能电站主要以电化学储能为主[4]。为保证光伏消纳能力和电网安全，目前多地已出台相关政策[5-6]。但国内外关于光伏储能配置优化相关的研究相对较少。例如文献[7]使用野马优化算法进行配置；文献[8]将碳排放量纳入光储充电站的考核指标进行配置；文献[9]通过k-means 聚类算法将光伏出力数据聚类，以弃光率为目标进行配置。

文中提出了基于哈里斯鹰优化(Harris Hawk Optimization,HHO)算法的光储容量配置优化方法，在低成本和高平抑波动性能上均取得较好的效果。

1 系统模型

1.1 光伏出力

采用青海某光伏电站2021 年全年发电功率数据，经过对当日累计发电量的聚类和简单的归纳统计即可得到晴天、多云、阴天、雨雪四种典型天气[10]下日内波动程度最大的光伏日发电功率曲线，如图1所示。同时，除这四种典型天气以外，还存在故障和检修状态，在这种状态下光伏电站无发电量。四种典型天气天数和占比分别为晴天66天（占18.08%）、多云119 天（占32.6%）、阴天92 天（占25.21%）、雨雪49 天（占13.42%）。同时，故障/检修39 天（占10.69%）。

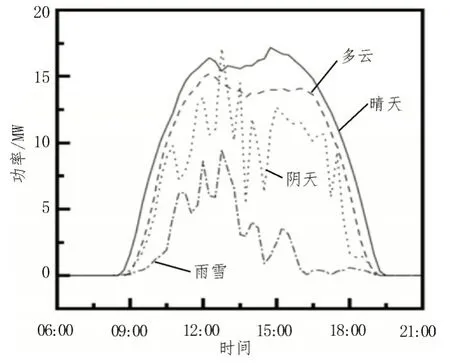
图1 不同天气类型下的典型日发电功率曲线

1.2 优化目标函数

首要的优化目标是更小的出力波动，其数学表达式为：

式中，n为工作时刻点的个数；r(τ)是在τ时刻光伏的波动率，可根据式（2）计算：

式中，Ps(τ)是在τ时刻光伏的发电功率。

其次的优化目标是更低的成本，即F2=minC。其中，总成本C包括建设成本Ccon和运维成本Crun。建设成本根据单位容量进行年计算，按照2022 年6月部分储能EPC 项目中标结果，取为1.5 元/W·h 和0.5 元/W。储能运维成本认为与年吞吐电量有关[11]，在文中取为0.01 元/kW·h。综合上述，最外层的优化目标可写为：

式中，Eb,c是储能系统的额定容量；Eb,p是储能系统的额定功率；Wb是储能系统平均年吞吐电量；L是储能系统的预期使用寿命，取为10 年。

1.3 约束条件

1.3.1 荷电状态约束

基于某头部储能电池公司生产的磷酸铁锂电池集成储能电站，电芯额定容量为280 Ah。为了延长储能电池的使用寿命，同时保证其运行状态[12]，需要满足储能电池的荷电状态SOC[13]约束：

式中，SOC(τ)为τ时刻结束时的荷电状态；δ为储能电池的自放电率；η为储能电池的直流侧充放电效率，下角标c和d分别表示充电和放电，二者均取为0.87；Pb为储能电池在τ时刻的充放电功率，充电时为正，放电时为负；Δτ为时间间隔；而SOCmin和SOCmax分别为允许的最小和最大荷电状态，满足此条件可避免储能电池的过充、过放，分别取为10%和100%。

1.3.2 容量约束

储能系统在充放电过程中容量不应超越电池容量的上下限，即：

式中，Eb,max和Eb,min分别为储能系统在τ时刻可使用能量的下限和上限，可通过式（6）与荷电状态进行关联：

1.3.3 功率约束

储能系统的功率约束包括功率平衡约束和最大充放电功率约束。功率平衡约束如以下公式：

式中，Pb(τ)为储能电池的功率，充电时为负，放电时为正；Pl(τ)为负荷功率，这里取为光伏电站的并网功率。

最大充放电功率约束需要满足以下公式：

式中，Pb,max为储能系统允许的最大充放电功率。

需要注意的是，储能系统中所剩余的电量是有限的，因此实际的功率约束为：

2 基于哈里斯鹰优化算法的优化方法

哈里斯鹰优化（HHO）算法是Heidari 等人于2019年提出的群智能算法。HHO算法调整参数少、收敛快，较为适合解决工程问题[14]。该算法主要分为全局搜索（Exploration）和局部开发（Exploitation）两个阶段[15]，主要流程如图2 所示。

图2 哈里斯鹰优化算法的主要流程

在使用哈里斯鹰优化算法对储能电站容量进行优化配置时，首先需获得光伏电站的全年出力曲线和储能系统参数，用以确定原始数据波动情况和储能调节能力，然后以最低的光伏功率平均波动率为首要的优化目标，储能系统成本为次要目标，储能运行参数（如电池SOC 等）作为约束条件，以储能功率作为哈里斯鹰的位置向量，使用哈里斯鹰优化算法进行优化配置。

2.1 全局搜索阶段

在全局搜索阶段，哈里斯鹰会随机地分布位置，并且通过以下两种策略更新位置：

式中，t是当前迭代次数；X(t)是哈里斯鹰的位置向量，在文中代表了储能电池的功率；Xrand(t)是从鹰群中选择的随机个体；Xm(t)是鹰群的平均位置，可通过式（11）进行计算；N是鹰群中哈里斯鹰的数量；Xprey(t)是猎物的位置；ri及q是处于(0,1)之间的随机数；lb和ub分别是变量值的上下限。

2.2 过渡阶段

哈里斯鹰会根据猎物逃逸所需要的能量E来决定是否进入局部开发阶段或是仍然进行全局搜索，逃逸能量的计算可表示为：

式中，E0是猎物的初始能量，-1 ≤E0≤1；T是最大迭代次数。

当 |E|＞1 时，哈里斯鹰仍停留在全局搜索阶段，而不会进入后续的局部开发阶段。

2.3 局部开发阶段

在局部开发阶段，哈里斯鹰根据猎物逃逸能量E和逃逸概率r来判断需要采取的行动，可以分为软包围、硬包围、渐进式快速俯冲的软包围和渐进式快速俯冲的硬包围四种策略[16]。

3 算例分析

3.1 参数设置

首先根据聚类所得到的四种典型天气，在Matlab 中编写程序进行实验，实现基于哈里斯鹰优化算法的储能容量优化。其次，根据单日优化所得到的数据和结论，对全年进行优化和对比。

为了方便计算，储能系统的初始SOC 取为50%，允许的最大、最小荷电状态分别为100%、10%，哈里斯鹰算法的迭代次数为1 000 次，种群个数视数据量而定，每个哈里斯鹰个体代表在该时刻储能系统的工作状态，按照哈里斯鹰算法和约束条件更新个体位置。

3.2 不同天气下单日优化结果与分析

在外层给定了一组容量和功率的条件下，内层以波动率为优化目标的功率和容量便已确定。当给定一种配置容量即功率2.5 MW、容量5 MW·h 时，不同天气下的优化结果如图3 所示，优化前后平均波动率如表1 所示，收敛曲线如图4 所示。

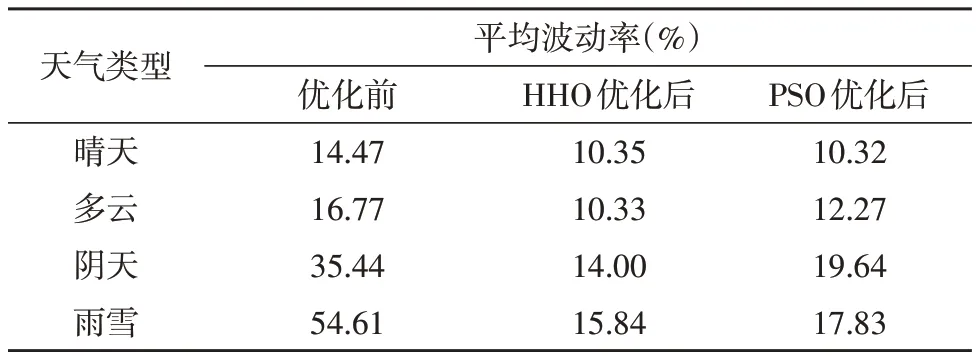
表1 四种典型工况优化前后平均波动率

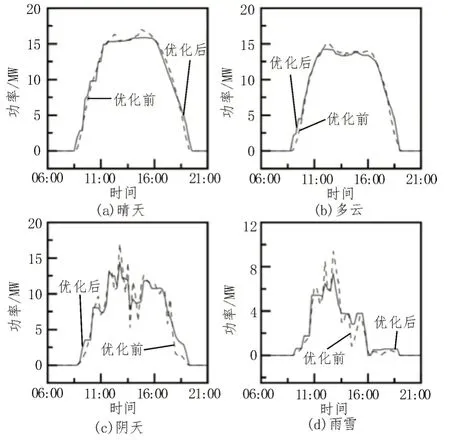
图3 四种典型工况优化前后功率曲线

图4 四种典型工况的HHO和PSO收敛曲线

对比图3 中优化前、后的功率可知，对于晴天、多云这两个天气情况较好的工况，在午间约12:00-15:00 时间段可较好地平抑波动。同时对于阴天、雨雪两个工作条件较差的工况，较好地实现了对光伏发电功率的“削峰填谷”，减轻该光伏电站并网后功率波动对于电网的冲击。四种工况优化前后的功率对比表明，所提出的优化模型可以实现对目标函数的优化。

结合表1 和图4 可以得到，随着迭代次数的增加，平均波动率函数值逐渐减小，对于晴天和多云天气，可以在约200 次迭代后分别达到10.35%和10.33%的最优平均波动率；而对于运行情况较为复杂的晴天和多云天气，则需要约600～800 次迭代后分别达到14.00%和15.84%的平均波动率。同时，图4 也对比了HHO 与粒子群优化算法（PSO）的收敛曲线，与较为常规的优化算法PSO 相比，HHO 具有收敛快、不容易陷入局部最优解等优点。因此，若给定一种配置，在相同的迭代次数下，HHO 往往可以达到更低的平均波动率。为了达到相同的平抑波动效果，使用PSO 的优化模型比HHO 需要更大的功率和容量。

图5 所示为在变储能功率、容量的条件下，四种天气在该储能配置下所能得到的最优平均波动率三维图。从该图中可以得到以下结论：①储能的功率和容量会对平均波动率产生影响，当功率、容量增加时，平均波动率随之减小。②对于阴天、雨雪等天气情况较恶劣的工况，容量变化对平均波动率的影响较功率更大。③对于所有天气下的工况，功率3 MW、容量6 MW·h时基本可以达到最优的平均波动率，此时若再增加储能系统的功率和容量，优化后的平均波动率不会产生明显的变化，反而会增加投资，降低经济性。

图5 四种典型工况平均波动率变化的三维图

图6 所示为四种典型工况经过上述优化后，所获得的储能运行功率曲线和SOC 变化曲线。从图6中可以得知，除阴天工况储能功率到达极限值外，其余三种天气下，配置储能2.5 MW、5 MW·h已可以满足全天获得最低平均波动率。图7所示为阴天在5 MW、10 MW·h 优化后的功率曲线和储能运行曲线，优化后平均波动率降低至9.72%。

图6 四种典型工况的储能功率和SOC曲线

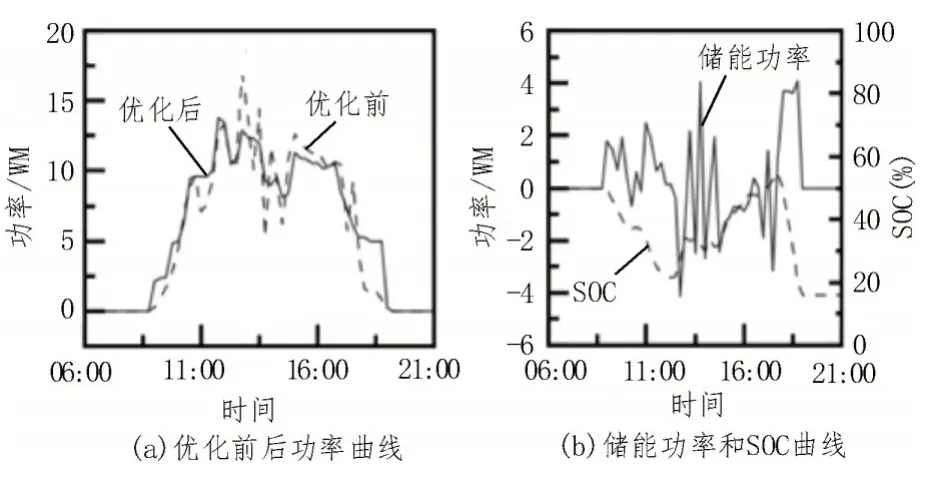
图7 阴天在5 MW、10 MW·h优化后的功率曲线和储能运行曲线

阴天工况仅占比25.21%，为了下降约4%的平均波动率而将储能功率和容量扩大一倍显然是不划算的。因此，仍然采用图3 所示的最佳储能运行功率来对成本进行优化。类似地，借助哈里斯鹰优化算法，可以得到四种工况下储能系统需要配置的容量和功率，如表2 所示。

表2 四种典型工况的储能容量和功率配置

3.3 全年优化结果与分析

通过对四种典型天气下的配置优化，可获得各自对应的最佳储能功率和容量，为了满足全年的运行需求，分别取每项的较大者，即容量4.59 MW·h、功率2.5 MW。全年优化的基本逻辑与对典型工况的单日优化类似，区别在于单日优化每日起始SOC 均为50%；而全年优化仅1 月1 日起始SOC 为50%，1 月2 日的起始SOC 为1 月1 日经过优化后当日结束时的SOC，以此类推。

经过对全年的运行数据使用哈里斯鹰优化算法进行分析优化，全年平均波动率（计入故障/检修天数）从19.41%降低至11.33%，储能系统年吞吐量为1 250.18 MW·h，10 年期计算的总成本合计814.75万元。所提出的储能优化光伏出力模式主要用以降低新能源出力波动对电网造成的冲击影响，根据该光伏电站往年受西北两个细则考核情况，每年可以减少考核25 万元，同时，储能电站等效小时数为500 小时，满足青海储能补贴政策的有限保障消纳540 小时，该部分电量电价无需参加市场化交易。

4 结论

文中提出一种基于哈里斯鹰优化算法的储能配置优化模型，以全天平均波动率最低为主要目标，最低成本为次要目标，进行了双层优化。通过对四种典型天气情况下进行分析，获得在该工况下最佳的储能容量和功率。同时根据这四种储能配置方案，分别选取最大的容量和功率后，对全年进行优化以验证有效性。经过建模和算例分析，可以得到以下结论：

1）所采用的哈里斯鹰优化算法，对于解决储能电站配置问题有比较好的表现，对于阴天、雨雪等工作条件较差的工况，可以将平均波动率从35%～55%平滑至约15%。同时，通过模型训练结果对比，哈里斯鹰优化算法相比于传统的粒子群算法在光伏电站配储容量优化上具有更好的平抑波动效果；

2）对不同天气分别进行优化的模式可以规避单日优化不同工况所带来的配置结果偏差，同时可以满足全年的平滑波动需求，将全年平均波动率从19.41%降低至11.33%；

3）对于光伏电站的储能配置应当根据实际需求进行，简单地按照一定比例配置储能，可能会导致成本过高、资源浪费或运行不理想等情况，建议在新能源配储过程中考虑新能源实际出力情况进行配置。