高铁振动信号的频率提取与定频降噪

汪寅章，郝学元

（南京邮电大学电子与光学工程学院，江苏南京 210000）

高铁以高速运行，必然会造成较强的环境振动，一方面会对人的精神和身体产生较大的危害[1]；另一方面还会严重影响机器或各种精密仪器的使用[2]。

在以往对轨道交通振动的研究中，国外的研究方向主要集中于不同属性的地面、不同轨道和不同车体结构对振动的影响[3-5]。国内方面，有研究指出，周期或类周期频谱峰可以用于检测铁路安全。列车本身的各项因素对振动特性的影响，为防震工作做出了指引，并提取出了列车产生的主要噪声频率，且给出相应频率声波的防范措施[6-8]。

主动噪声控制（Active Noise Control，ANC）技术雏形早在1936 年就被德国物理学家PAUL LEUG提出。国外对其在低频信号方面的降噪表明其有较好的降噪作用[9-10]；国内方面对该领域的研究较晚，主要将其应用于航天与汽车方面[11-15]。ANC 技术发展至今日，由美国人BURGRESS[16]提出的滤波-X 最小均方（FxLMS）算法已成为主动噪声控制算法应用最广泛的算法之一，并且有了多种改进型[16-17]。

基于此，文中采用多组节点采集数据，对高铁振动信号进行分析，提取出信号的主要频点；并使用ANC 技术，对主流FxLMS 算法进行实时性和定频性优化，针对提取出的特定频点进行降噪处理，从而消除或减弱高铁振动对周围环境的影响。

1 同步压缩小波变换原理

2011 年，DAUBECHIES 等人首次提出了同步压缩小波变换这一信号处理技术。同步压缩小波变换是在小波变换和快速傅里叶变换等其他时频分析方法的基础上，通过压缩时频曲线来锐化时频域分辨率的一种新的时频分析方法。主要步骤如下：

1）首先根据待分析信号的特征选择合适的小波母函数，随后对待分析信号s(t)进行连续小波变换，从而得到小波系数Wx(a,b)。

2）对小波系数Wx(a,b) 求时间偏导，获得瞬时频率Wxk(a,b)，进而可以使得小波变换后的时间-尺度平面转换为时间-频率平面。

3）根据时频谱重排的基本思想，任选某一中心频率，随后挤压时频面上的小波系数在已选定某一中心频率附近区域值，进而获得时频平面上的同步挤压变换量值。

2 高铁振动信号主频提取

在河北某地放置了若干振动检测设备，用以收集高铁经过时轨道的振动数据。在垂直铁轨方向上，每隔约90 m 放置一个检测设备，用以采集高速列车经过时产生的振动信号。回收解析设备采集到的数据，查看全部采集到的时段信号波形，筛选出设备位置合适、数据完整、没有损坏、具有代表性的实测数据段进行分析，最终选定四个设备中同一时段采集到的振动信号。长时段的信号波形如图1 所示，选取某一时间点为相对时间零点，并将数据归一化处理，文中振幅均为归一化振幅，以便于管理数据。从图1 中可以看出，部分采集到的数据有明显异常，其数值远超过正常范围，该部分数据不予使用。选定相对时间零点起，25 s 时间段内（25 000 个采集点）的数据段加以分析，选定段的采集点波形图如图2 所示。

图1 长时段信号波形

图2 各点选定时段信号波形

四个采集设备垂直于铁轨方向分布，分别将其命名为A、B、C、D 四个点。截取四个点某一时段的振动信号，时间域上四个点采集到的振动信号波形如图3 所示。

图3 各采样点时间域振动谱图

从图3 可以看出，四个采集点采集到的信号在时间上同步，并且随着距离的增加，振动信号在幅度上逐渐减弱。

对四段信号进行同步压缩小波变换，查看信号的时频域特性，四个采集点信号的时频谱图如图4所示。

图4 各点信号时频谱图

从图4 可以看出，A 点距离高铁轨道最近，所以产生的振幅也最大，高强度的有效信号持续时间也最长，大约为10 s。在10 Hz 和20 Hz 频率附近，信号强度最大，说明高铁产生的振动主要为低频信号，且振动能量主要集中在这两个频率。在频谱图的5～15 s时间段中可以看出，低频的高强度高亮信号充满了这个时间段；在时域图中，5～15 s 为强振幅的振动信号，时间域谱图的波形与时频谱图的特性相吻合。

对比A 点，图4 中B 采集点的信号频率分布较为分散，除了低频的10 Hz 左右主峰频率信号外，次峰频率分解为两个频率，分别为20 Hz 和30 Hz 左右，并且在时间分布上不具有连续性，参见图5。由于信号频率的分解，信号能量也随之分散，所以该点次峰信号在强度上较为明显地弱于B 点的主峰信号和A点的次峰信号。

李闺女又呸了一口：李六如，真是越来越不知道羞耻了。原先拆迁时，你想当个先进也就算了。如今，又勾结佟金鑫占了那点口粮田。你说，老少爷们今后怎么活？

图5 B点信号时频谱图

从图5 可以看出，振动信号在B 点处出现了频率分解现象。10 Hz 频点的信号得到保留，而20 Hz 频点的信号分解出两条次峰信号，其传播到C 点时，其中较低频率的信号衰减较为迅速，在频谱图上的谱线强度不足，只剩下具有一定强度的30 Hz 左右的次峰信号。在D 点10 Hz 主峰信号强度衰减到了A 点的43%，而D 点的次峰信号强度甚至衰减到了A 点的1/6。

横向对比四个点的时频域谱图可以发现，高铁振动产生的主要信号集中在10～30 Hz，在不考虑频率分解的情况下，主要为10 Hz 和20 Hz 两个频点。

3 高铁振动信号针对性防治

从上一节分析结果可以看出，高铁产生的振动主要集中在30 Hz 以下的频段，且能量较大。为了消除或降低这些低频高能量信号，减弱其给周边环境和仪器设备等带来的影响与危害[9]，利用主动噪声控制（ANC）技术，并对其中主流的FxLMS 算法做了实时性和定频性优化，针对性地对低频信号进行实时降噪处理。

ANC 技术是利用声波的相干相消原理，构建一个与原信号频率、幅度相同但相位相反的声波信号，使两者相互叠加抵消，从而消除或减弱噪声。目前ANC 技术使用的主流算法为FxLMS 算法，这一算法为LMS 算法的改进型，其具有收敛速度快、自适应滤波等主要功能，能对一定频谱范围内的声波进行自适应降噪[10]。

使用FxLMS 算法对构建的随机声波信号进行降噪处理，仿真结果如图6 所示。

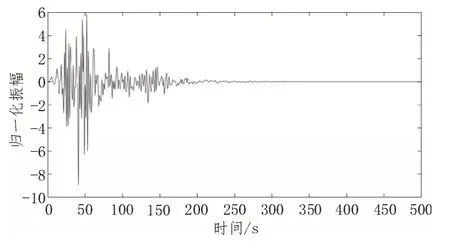
图6 随机噪声去噪仿真图

从图6 可以看出，随着时间的推移，在约90 s 以后声波信号得到了有效的抑制；在持续自适应去噪的条件下，200 s 以后声波信号基本得到了消除。但结合前文的分析及时域、时频谱图可以看出，高铁振动信号具有短时性。由于高铁行驶速度较快，针对某一监测点的振动持续时间一般在20 s 以内，宽频降噪的时间远超过这一范围。在这种情况下，具备了自适应功能的宽频降噪系统将不具备实时性，且不具有实际意义。为了解决这一问题，文中基于FxLMS 算法，并对其进行定频优化，结合前文提取出的高铁振动信号的主要频率，对特定频点进行针对性降噪。

在一般的设计中，首先用传感器采集声波信号，其传输给CPU 后会有一定的处理和分析频谱和相位的过程，随后再针对这一频率和相位进行自适应降噪。为了简化这一过程，在传感器接收到信号后，采用FFT 快速分析信号，使扬声器直接针对10 Hz 和20 Hz 噪声产生抵消声波，简化了频率分析的过程。相位方面，由于系统的放置点在高铁线路周边的固定位置，加之其周边环境一般不会产生较大变化，则可以认为声波传播过来时相位较为固定，因而可以对抵消声波预设某一相位，使之与噪声源的原始相位差在180°左右，从而减少自适应的迭代次数，以便加快去噪过程，达到及时、快速消除高铁定频噪声的目的。

基于以上分析，对10 Hz 和20 Hz 的混合噪声进行降噪模拟，优化后的降噪结果与局部放大图如图7所示。

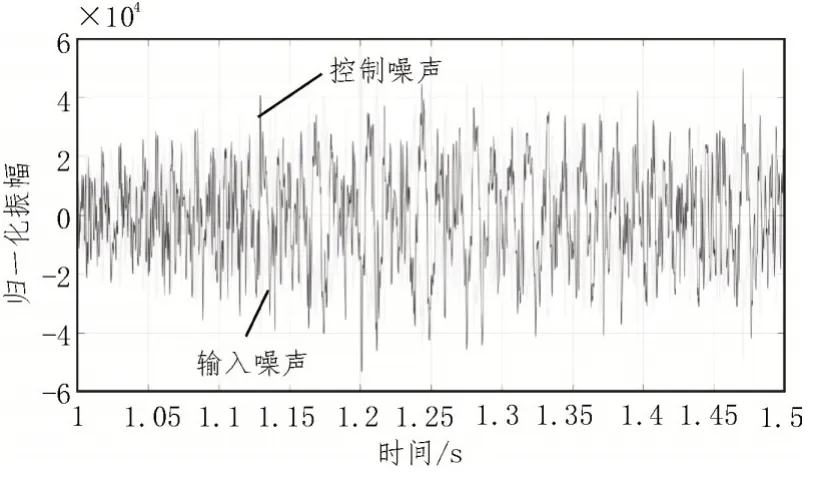
图7 10 Hz和20 Hz针对性降噪局部效果

图中浅色为原始信号（输入噪声），深色为抵消信号（控制噪声）。从图中可以看出，原始信号和抵消信号时间同步性较好，抵消信号对原始信号跟踪稳定，并且幅度和相位持续保持一致，可以认为具有良好的去噪效果。

结合以上仿真结果可以认为，在前文对高铁振动信号的时频特性和传播特性做了一定程度的研究后，可以提取出其主要振动频率，再结合ANC 技术与FxLMS 算法，对高铁产生的特定频率的信号进行针对性去噪处理，从而可以改善高铁轨道周边的环境，减少低频声波对人体、精密仪器和重要设备的影响。

4 结论

文中主要利用同步压缩小波变换技术，对河北某地高铁高架桥布置多组振动节点，对采集的实测高铁振动信号进行时频域分析、提取信号主频，并借助时域和频域谱加以验证，再对以FxLMS 为主的主动噪声控制技术进行优化，针对提取出的高铁主要振动频率声波进行降噪。

1）信号主频方面，高速列车产生的振动信号主要为低频信号，主频率峰大约为10 Hz。主峰附近有伴生信号，其频率与主峰接近，在时频域谱上重合为一条信号谱线。主峰信号振幅随传播距离的衰减较弱，传播距离较远，有一定的危害性。

2）除了主峰信号外，高铁振动还产生了少量次峰信号，频率大约为20 Hz 及其附近频率，其信号强度稍弱于主峰信号。高铁振动产生的信号波频率一般在30 Hz 以下频段，主要集中在10 Hz 和20 Hz 这两个频率。

3）降噪方面，对FxLMS 算法进行了实时性和定频性优化，增强了定频去噪的针对性，简化了相位识别和自适应的过程，从而提高了降噪效率。在优化与精简了主流的FxLMS 算法后，使之在高铁短时经过某点时可快速抵消定频噪声，最大程度上消除或降低高铁低频噪声的危害。同时可以认为这种更具有定频性和实时性的ANC 主动降噪技术还可以用于其他具有定频噪声的场合，对噪声防治具有一定的实际意义。