基于神经网络的跨介质飞行器水面弹跳运动参数快速预测方法
任帆涛,姜 毅,王斯艺,覃通明
(北京理工大学宇航学院,北京 100081)
1 引 言
现代海洋活动中,随着雷达侦测技术以及先进航行器技术的快速发展,传统单介质的无人航行、潜航平台在信息搜索、地势勘测等方面的优势逐渐降低。近年来,受生活中颇多生物现象的启发,研究学者设计出一款同时具有水面飞行器、水面快速舰艇及水下航行器优势的新概念飞行器,其可以适应不同介质的飞行环境,快速实现遂域切换,大幅提升了现有单一介质飞行器的性能[1]。
目前,国内外学者针对跨介质飞行器开展了大量的研究工作,主要包括跨介质变体技术、跨介质及多相流动耦合现象解析、实战决策等。谭骏怡等[2]基于一种特殊的双层半环形闭合翼构型,对该构型跨越水空介质后的变体过程进行研究,分析发现机翼回收过程的气动参数较大是因为受到了流场迟滞的影响。李宜果[3]等针对跨介质飞行器高速冲击水面时的空泡壁面变化特征进行分析验证,给出了不同激励条件下空泡演化特性的时间分布特征。侯东伯[4]针对复杂外形的航行体击水弹跳现象进行试验验证,对该过程中航行体的两相轨迹及自身姿态调整进行分析,给出攻角、速度等参数对航行体运动特性的普遍影响规律。Hewiit 等[5]利用自主定制的试验装置针对方形平板在浅水中的连续弹跳问题进行研究,构建了更为可靠、贴近实际问题的弹跳有限元分析方法。Murali 等[6]针对锥头弹体的击水弹跳过程开展研究,根据能量守恒定律提出:相同击水条件下,锥头弹体的弹跳次数相比圆盘更少。Li等[7]提出一种空中控制、水下自由的单一控制策略,构建航行体低速冲击水面的有限元模型,模拟入水冲击过程,给出了不同冲击速度工况下跨介质飞行器入水姿态变化规律。
根据文献调研,当前国内外学者针对跨介质飞行器的研究主要通过数值计算仿真[2,4]以及试验手段[5,7]实现。然而,在实际弹跳运动中航行体运动状态具有随机性和未知性,相关参数或构型在不同情景下的运动状态难以预测。同时,跨介质飞行器的种类较多,主要包括踏板型、圆柱形、圆截头状以及透镜型等,其仿真模型计算难度大,耗费时间长,往往花费较多的人力物力。因此,在满足精度及可靠性的前提下,有必要寻求一种可降低研究成本的跨介质飞行器水面弹跳运动参数快速预测方法。当前,深度学习技术快速发展[8],在诸多领域中得到应用,有效解决了许多难题。然而,将深度学习迁移应用于跨介质飞行器领域的研究较少,因此有必要开展跨介质飞行器与深度学习的融合研究。
本文引入3 种不同的神经网络回归近似模型,快速预测跨介质飞行器水面弹跳运动参数。通过误差可信度、方差以及残差分析分别讨论了不同近似模型在跨介质飞行器水面弹跳运动参数快速预测中的优劣势。此外,本文提出了一种水面弹跳运动参数的近似迭代建模方法,通过分割样本集在训练过程评估回归预测算法的近似精度,并通过测试样本集的预测表现验证了该方法的有效性。
2 跨介质飞行器水面弹跳模型
2.1 物理模型
本文研究的跨介质飞行器水面弹跳布局选用文献[9]中的回转体构型,整体为类飞盘形。该飞行器原型为一款高超音速导弹,其尾部带有小型冲压发动机,可实现高超音速飞行[10]。通过简化后的跨介质飞行器外形布局如图1 所示,厚度变化规律如式(1)所示。跨介质飞行器的直径为1.80 m,最大厚度为0.23 m,质量为180.00kg,其转动惯量lxx=lzz=11.27 kg/m2,轴向转动惯量lyy=21.73 kg/m2,质心位置为图1中O点。
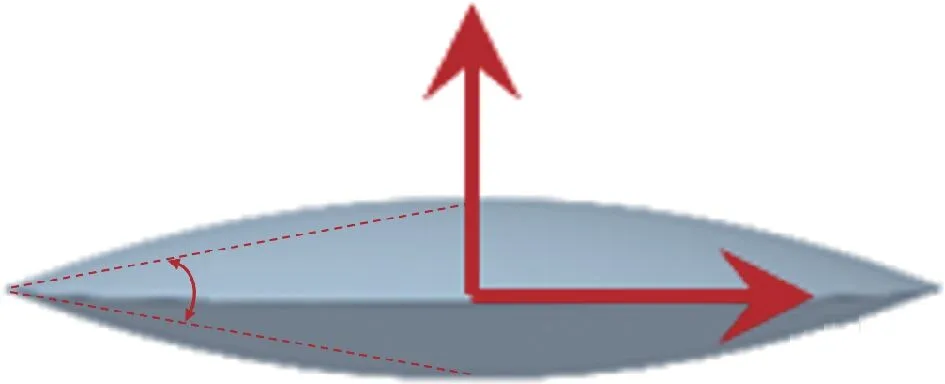
图1 跨介质飞行器水面弹跳构型Fig.1 Configuration of trans-media vehicle on water-skipping
本文采用移动半隐式粒子(Moving Particle Semi-implicit,MPS)仿真[11-17]方法计算航行体在水面弹跳不同情景下的速度衰减,其中粒子的表面判断系数为0.97,碰撞系数为0.2,湍流模型的Smagorinsky 定数取值为0.15。此外,计算域设置为6 m×15 m×4.5 m,初始粒子间距0.003m,粒子总数2830000,求解时间步长为0.05 ms,水中声速取1500.00m/s,初始粒子排布及作用半径如图2 所示,解析域中的粒子经概率碰撞实现物理参数传递,碰撞概率由概率密度函数计算得到。
2.2 跨介质飞行器弹跳模型校验
本节对建立的跨介质飞行器水面弹跳数值仿真模型进行校验,保证本文工作的可信性和有效性。根据郭子涛[18]实验中的平头圆柱弹体垂直入水过程进行数值模拟,平头圆柱长25.4 mm,端面直径为12.56 mm,质量取25.1 g,初速度为119.5m/s。平头柱形弹体入水的速度衰减曲线随时间分布如图3所示,其误差计算公式为
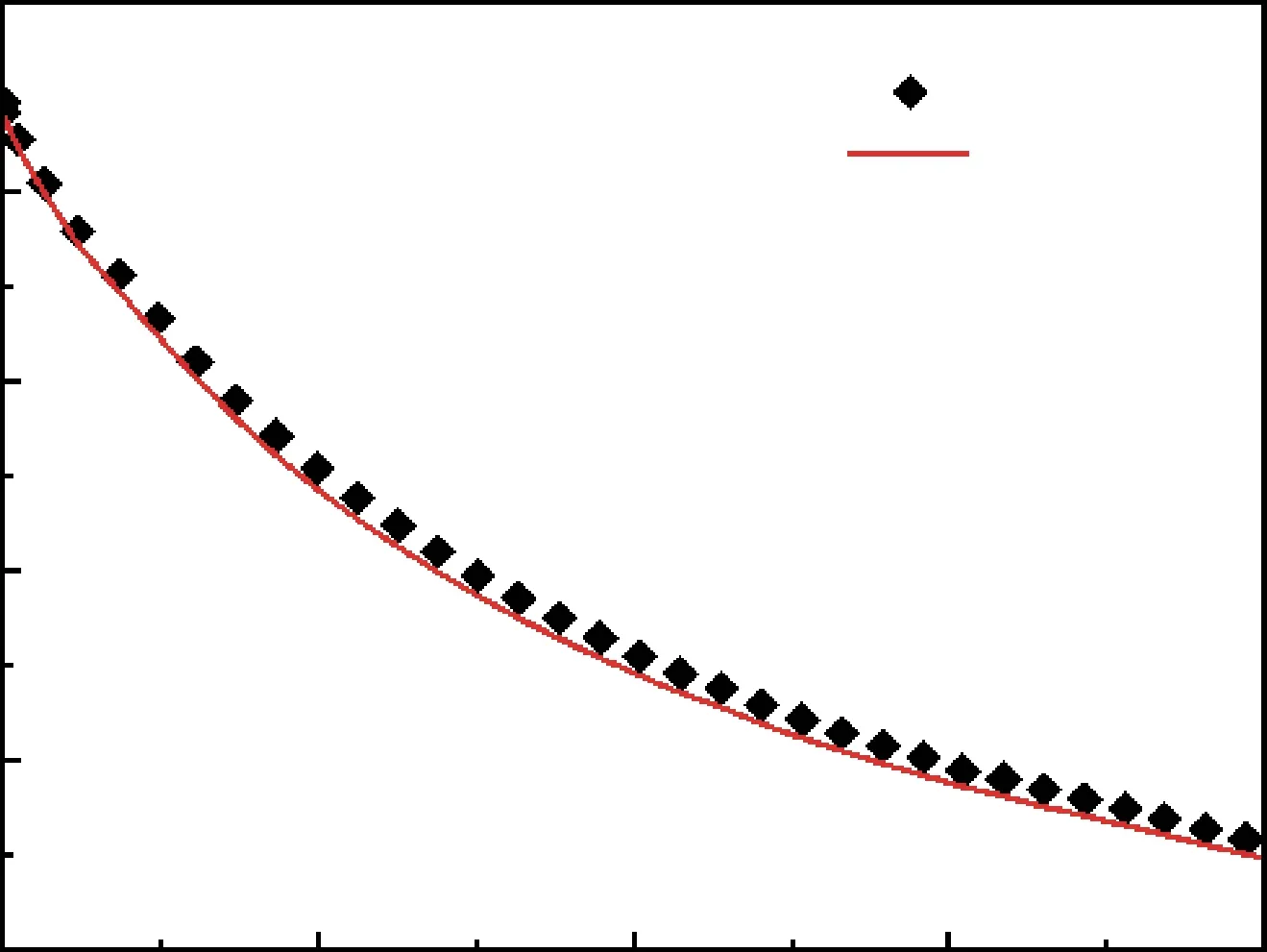
图3 平头圆柱速度变化曲线Fig.3 Velocity of the flat head cylinder
式中,vs为数值仿真的圆柱体入水速度衰减值,ve为实验中的平头圆柱弹体垂直入水过程中的速度衰减值。
根据图3 及式(2)计算可知,本文建立的跨介质飞行器水面弹跳计算模型得到的速度衰减分布与实验中得到的速度衰减分布规律基本一致,最大为8.07%,可以满足需求,从而验证了本文中跨介质飞行器水面弹跳MPS 数值计算模型的合理性与有效性。
为进一步验证数值模拟方法的准确性,本文用无网格粒子法对文献[19]中转速ω= 65 r/s、速度v= 3.5 m/s、攻角20°及弹道倾角20°实验条件下,铝制圆盘击水起跳过程进行数值模拟。图4(a)和图4(b)分别给出了高速摄影和MPS 数值计算得到的铝制圆盘击水起跳过程。观察圆盘开始接触水面到离开水面的过程,可以发现数值模拟结果与实验高速摄影相机拍摄到的圆盘姿态和液面破碎、飞溅变化规律基本一致,MPS 数值模拟结果与实验得到的液面凹形区域面积及水花散布形态高度吻合,数值计算与实验结果误差较小,进一步验证了本文采用的MPS 数值计算方法在计算水面弹跳运动方面具有一定的正确性和可靠性。

图4 数值模拟与试验值对比Fig.4 Comparison of numerical simulation and experimental values
3 水面弹跳运动参数近似预测模型
3.1 拉丁超立方试验方法
拉丁超立方抽样是一种在多维分布中生成参数值的近随机抽样方法,其可以通过有限迭代次数的抽样,比较准确地重建输入分布。拉丁超立方抽样方法的步骤如下:(1)将每一维度以互不交叉N等份平分,要求各个区间的采样概率相等;(2)在每一维度范围内随机选择样本点;(3)在每一维度内随机提取(2)中的点,使之组成向量集合。因此,针对m个不同输入的随机变量,分层抽样可以得到m×n个采样值。相比于蒙特卡洛随机抽样,拉丁超立方抽样产生样本的空间覆盖率更高。
3.2 神经网络算法近似模型
采用3种不同的跨介质飞行器水面弹跳近似模型:线性多元回归预测算法、反向传播(Back Propagation,BP)神经网络预测算法以及径向基函数(Radial Basis Function,RBF)神经网络预测算法,以跨介质飞行器水面弹跳参数(速度、俯仰角、弹道倾角和角速度)取样结果作为特征输入量,以跨介质飞行器水面弹跳后速度终值作为输出值,基于样本集的迭代计算获得3 种模型的回归系数或连接权重等参数,最终建立跨介质飞行器水面弹跳运动快速预测的神经网络近似模型。
3.2.1 线性多元回归模型
在研究过程中发现,部分参数如击水角度、航行体夹角等对跨介质飞行器水面弹跳运动参数的影响近似呈弱线性规律,因此考虑对航行体的水面弹跳运动参数建立线性多元回归模型并进行预测。
多元线性回归模型中待预测变量与特征因变量间的映射关系为
式中,y为预测变量值,k为样本总量,xi为样本特征变量的真值,βi为偏回归系数,ξ为随机误差项。
本文中跨介质飞行器水面弹跳运动参数与弹跳后速度参数组成样本空间,线性多元模型由最小二乘法拟合得到βi和ξ,由此建立跨介质飞行器的水面弹跳运动参数多元线性回归预测模型。
3.2.2 BP神经网络模型
BP 神经网络是一种基于误差逆向传递的前馈神经网络[20],其基本思路为:将输入参数利用隐含层进行归一化处理,在输出层形成预测近似值,同时通过输出层与期望值的误差调整网络的权值与偏置量,使得神经元的近似输出不断迭代逼近输出期望值。训练模型前需要对样本集数据进行归一化处理,迭代过程包括以下两部分:第一阶段正向传播,输入信号经由输入层、隐含层处理转化,逐层调整并过渡至输出层;第二阶段反向传播,误差函数从输出最高层反向传递至隐含层,最后过渡至输入最低层,并依次调节输入层到隐含层、隐含层至输出层的阈值和偏置。任意参数v的迭代方式为
依靠误差△v进行反向传播,式(4)可以对权值及阈值的参数迭代调整。其中,△v的迭代与学习率、激活函数的选取以及迭代误差计算相关。本文的BP 神经网络近似预测模型的激活函数为Sigmoid函数,实现方式为
图5提供了输入神经元u个、输出神经元v个及隐层神经元w个所构建的BP 神经网络拓扑示意图。假设第w个样本的真实速度预测输出值以yw表示,设定训练集T={(x1,y1),(x2,y2),…,(xu,yu)},xi∈Ru,yi∈Rw,及分别包含u、w个属性[21]的输入、输出层。隐层包含v个神经元,第u个输入神经元至第v个隐含神经元的连接权值为luv,第v个隐含神经元至第w个输出神经元的连接权值为mvw,zc为第c个隐含神经元的速度输出值。
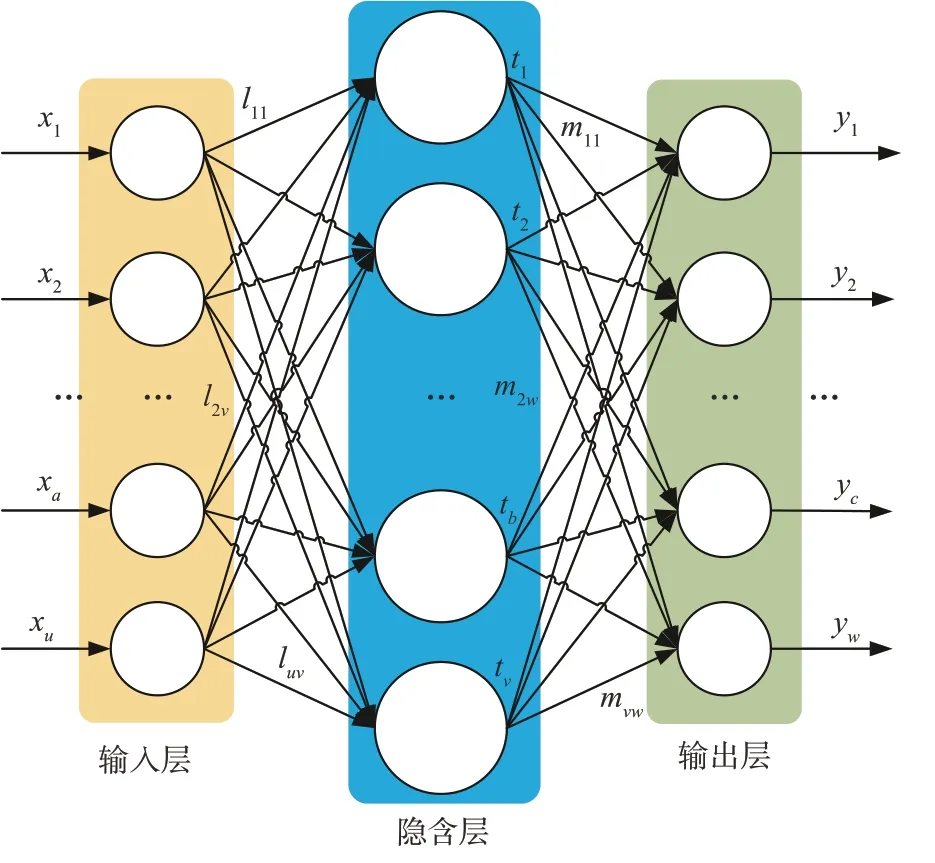
图5 BP神经网络拓扑结构Fig.5 Topological structure of BP neural network
本文建立神经网络模型的学习率初始值为0.001,隐含层的数量为2。同时,为保证神经网络预测模型训练过程的学习率能够根据训练状况进行自适应调整,在训练过程嵌入Adam算法以提升神经网络预测模型的收敛速度及预测性能。其中,Adam 算法中用于调整动量变量及均方梯度的一次超参数β1、二次超参数β2分别为0.85 与0.999,超参数ε设置为10-9,以防止迭代过程中分母出现0。
3.2.3 RBF神经网络模型
RBF 神经网络是一种三层神经网络[22],包括输入层、单隐层及输出层,从输入到隐层为非线性变换,隐层到输出层为线性变化,当神经元数量足够多时,理论上可以逼近任意函数。RBF 的隐含层神经元激活函数一般为一个仅依赖于偏离原点距离的实值函数,输出层是单隐层的线性叠加。设具有b维输入,输出为实值的RBF 神经网络[23]表示为
式中,神经元数量为k,αp和λp分别为第p层神经元的中心及权值,w(x,αp)表示样本点到中心点的距离。本文中所用的高斯核函数如式(7),σi为带宽。
3.3 近似流程建模
为降低跨介质飞行器水面弹跳运动参数的计算成本,本文采用拉丁超立方试验设计方法获取样本集,通过引入神经网络算法进行近似参数表征,以实现跨介质飞行器水面弹跳运动参数的快速预测。图6 为跨介质飞行器水面弹跳运动参数快速预测的神经网络模型构建流程。
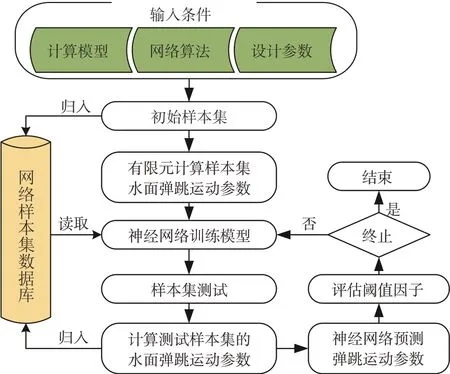
图6 神经网络近似表征模型流程图Fig.6 Approximation modeling process using neural network
步骤1:采用拉丁超立方试验方法在飞行器运动速度、入水角度、自旋角速度以及航行体倾角取值范围内构成的超空间内进行抽样,随机生成ne个初始样本集,其中包括训练样本集、校验样本集和测试样本集。
步骤2:通过调用跨介质飞行器水面弹跳模型,计算初始样本集不同运动速度、入水角度、自旋角速度以及航行体倾角下跨介质飞行器水面弹跳后的速度真值,并将其作为样本输出集合。
步骤3:训练近似预测模型。基于训练样本点对应的水面弹跳速度,建立线性多元回归、BP 神经网络以及RBF 神经网络共3 种近似预测模型。由于水面弹跳后的侧向速度相较于垂向速度和轴向速度可以忽略,因此仅对垂向速度vz与轴向速度vx进行训练。
通过拉丁超立方试验设计方法生成校验样本,调用跨介质飞行器水面弹跳MPS 计算模型获取校验样本点处速度值[vz,i, ]vx,i,,i= 1,2,…,nv,以分割样本集合的方式评判预测模型的近似精度[24]。
步骤4:方差分析中引入离均差平方和R2与相对平均值的误差ERA作为回归因子。设̂表示样本点的速度预测,为样本真实的平均速度,离均差平方和可表示为式(8),ERA可表示为式(9)。若离均差平方和大于设定许用离均差平方和,则返回步骤3;否则,进入下一步。
步骤5:输出经过校验的水面弹跳参数快速预测模型,用于预测跨介质飞行器水面弹跳参数的变化规律。
4 预测算法有效性分析
针对跨介质飞行器水面弹跳参数预测问题,通过实际工程算例验证本文工作的有效性与准确性。在学习回归模型之前,需要对训练集各参数进行归一化处理,处理方式为
式中,xmin和xmax分别为训练集参数x的最大值和最小值。根据3.3 节中神经网络近似表征流程,跨介质飞行器水面弹跳运动参数取值范围如表1所示。

表1 特征参数及取值范围Table 1 Feature parameters and variable scope
采用拉丁超立方抽样设计方法,在表1所示参数取值区间内随机抽样,建立跨介质飞行器水面弹跳运动参数近似模型的256 个数据点,样本空间如表2所示。

表2 击水弹跳近似模型样本空间Table 2 Sample space table of approximate model under water-skipping
表3 展示了采用3.2 节中的3 种快速预测模型的误差指标计算结果。通过将测试集样本输入条件下的跨介质飞行器水面弹跳运动的速度预测值与MPS 数值仿真结果进行对比,得到以下结果:线性多元回归模型的预测结果误差主要分布在10%~25%之间,平均误差为19.59%,最大误差达到42.44%,最小误差为3.36%;跨介质飞行器水面弹跳运动的速度值较低时,预测误差较小,近似效果表现良好;对于运动速度大于130 m/s 的水面弹跳运动,其预测性能不佳。BP 神经网络模型的预测结果的误差最大达到35.55%,最小达到1.27%,平均误差为14.36%,对于运动速度大于130 m/s 的水面弹跳运动,其预测性能同样具有较大的误差,在低速水面弹跳运动中的平均误差分布较高,这可能是由于BP 神经网络中因样本稀疏出现迭代超参数维度与寻优难度,故而预测性能不佳。RBF 神经网络模型的预测结果的平均误差为8.39%,最大误差为28.66%,最小误差为0.56%,在全样本集内的误差普遍小于线性多元回归模型和BP 神经网络模型,具有良好的预测近似性能。
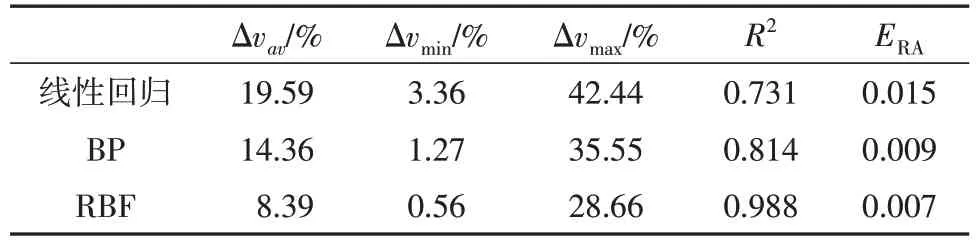
表3 近似模型误差分析Table 3 Error analysis of approximate model
采用离均差平方和对预测结果的方差进行分析。其中,R2越接近1,ERA越小,表明近似模型的结果准确度更高,模型的实用性更强。图7~9分别展示了3 种预测模型针对跨介质飞行器水面弹跳测试集的速度预测值与MPS 仿真速度值的方差分布。RBF 神经网络模型的回归系数R2值为0.988,相对平均值误差ERA为0.007,表明其预测回归拟合度较高,方差较小,近似预测的准确度较高,可靠性强;BP 神经网络模型以及线性多元回归模型的回归系数R2分别为0.814和0.731,相对平均值误差ERA分别为0.009与0.015,模型的近似准确度相比RBF 不够理想。BP 神经网络的预测结果准确度低的原因:预测模型训练过程的样本点数为256,样本集数量有限,而BP 神经网络本身多隐层神经网络的算法潜力发挥不足,导致预测结果较不理想。

图7 线性多元回归模型方差分析(R2 = 0.731)Fig.7 Variance analysis of linear multiple regression model
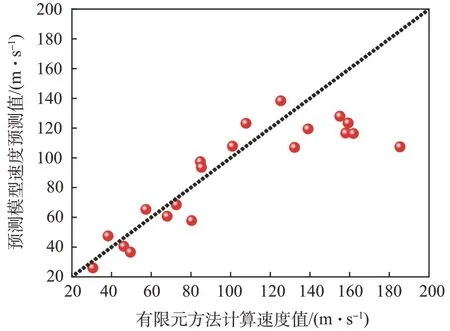
图8 BP神经网络模型方差分析(R2 = 0.814)Fig.8 Variance analysis of BP neural networks model
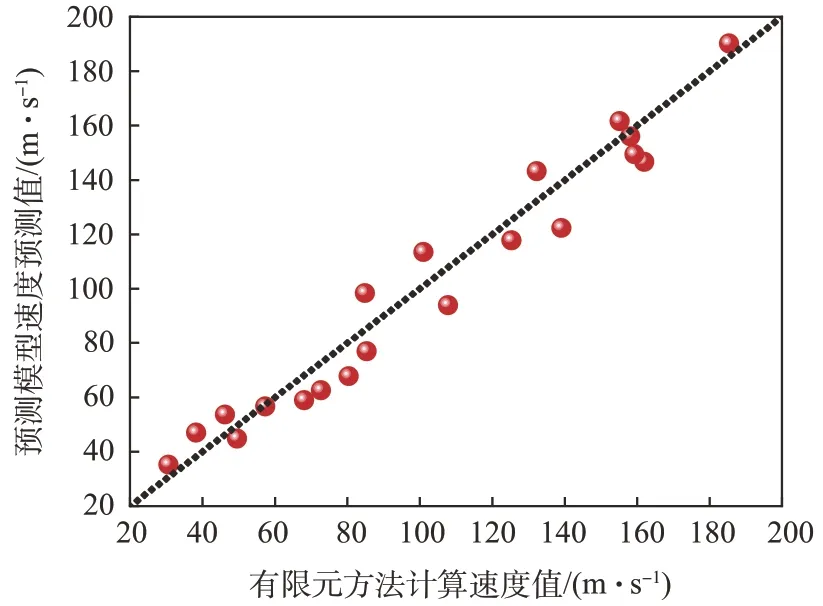
图9 RBF神经网络模型方差分析(R2 = 0.988)Fig.9 Variance analysis of RBF neural networks model
图10~12 分别为不同预测模型下跨介质飞行器水面弹跳运动速度的预测值和MPS 计算值的残差分布。纵向对比发现:线性多元回归模型参数预测的残差基本分布于±25 m/s以内,BP神经网络模型速度预测的残差值基本小于±30 m/s,两者预测残差均出现部分与实际相悖的异常值,导致参数预测结果的可信度明显下降;RBF 神经网络预测模型速度预测的残差值基本小于±15 m/s,在低速、高速击水中的残差分布明显均匀,未出现异常值。因此,RBF 神经网络预测模型对于跨介质飞行器水面弹跳参数的预测性能明显优于前二者。
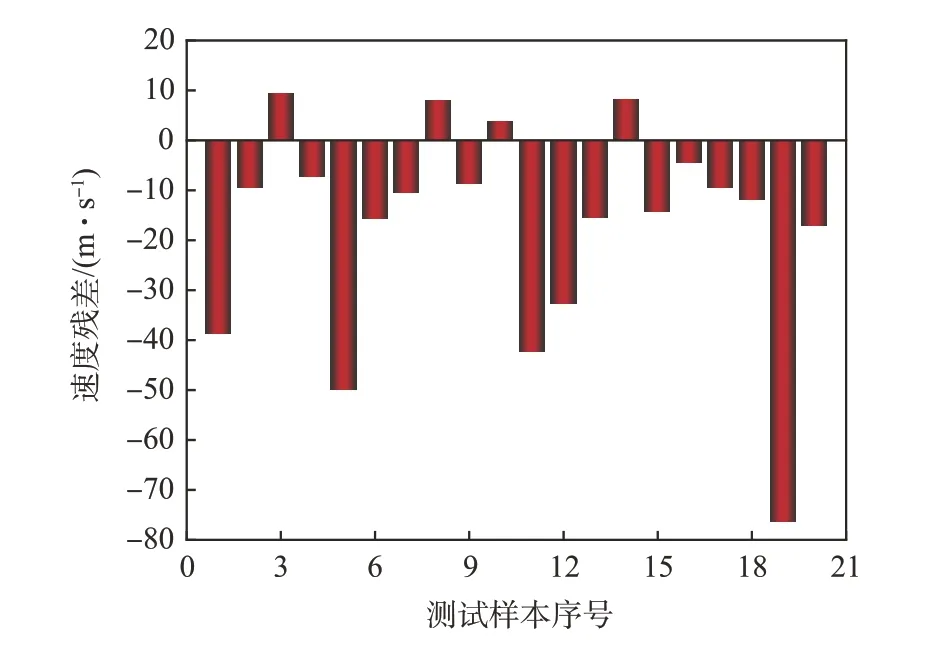
图10 线性多元回归模型残差分析Fig.10 Residual analysis of linear multiple regression model
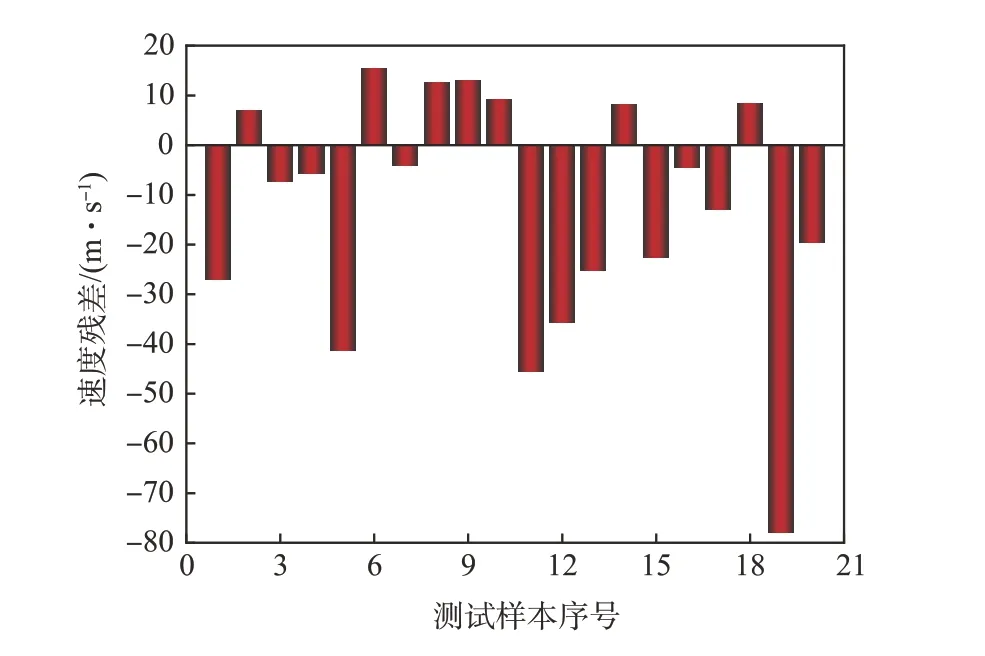
图11 BP神经网络模型残差分析Fig.11 Residual analysis of BP neural networks model
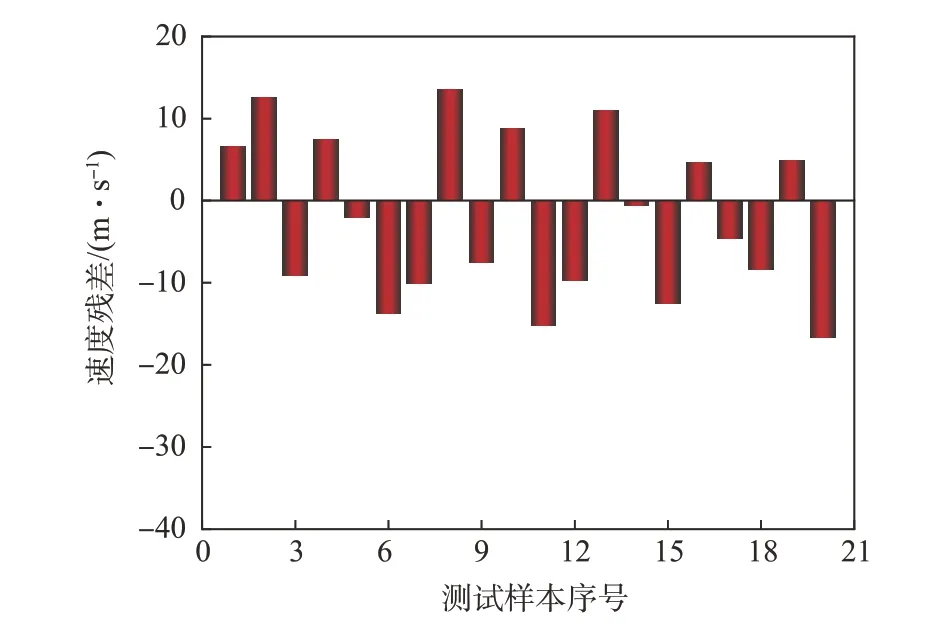
图12 RBF神经网络模型残差分析Fig.12 Residual analysis of RBF neural networks model
线性多元回归算法一般用来刻画单一被解释变量受多个解释变量的关系且通常要求两者满足线性映射关系。本文中跨介质飞行器的击水角度、速度等部分参数仅与水面弹跳后的运动参数呈弱线性关系,而其余影响因素如角速度、攻角等均保持非线性影响规律。
以上因素均会导致本文中多元线性回归模型的预测结果不理想。针对跨介质飞行器击水弹跳过程的非线性及耦合问题,需要依靠具有非线性映射能力的预测算法以提高预测性能。BP 神经网络算法及RBF 神经网络算法均可以用来刻画非线性模型,但两者在激励函数以及内部网络的映射方面具有一定的差异。对于相同精度要求的问题,BP 网络的结构要比RBF 更简单。BP 网络使用的激励函数为Sigmoid,其函数值在输入空间中无限大的范围内为非零值,而RBF 激励函数为高斯核函数,仅需要计算欧式距离,导致其内部结构不同。BP 算法一般通过梯度下降调节神经元的权值以逼近最小误差,容易陷入局部最优;而RBF 依靠核函数计算输入与函数中心点的距离调整权重值,具有全部逼近能力。由于BP 与RBF两者的激励函数以及网络结构差异,导致BP 与RBF 处理相同的问题时,RBF 的预测精度等性能一般都优于BP 网络[15],这与本文的试验结果相一致。同时,本文的样本点数量为256,样本集稀疏有限, BP 网络强大的多隐层映射能力发挥不足,这也是导致BP 网络性能较低的原因之一。
为进一步验证本文中近似预测模型方法的优势,对100 组测试样本下,数值仿真与回归模型分别预测跨介质飞行器水面弹跳运动速度的单工况平均计算时长耗费进行统计,结果如表4 与图13所示。线性多元回归预测模型、BP神经网络预测模型以及RBF 神经网络预测模型的单次击水弹跳参数预测平均时长耗费分别为0.31 s、0.21 s和4.72 s,而MPS仿真计算的耗费时长约为2.6 h。因此,本文中提出的RBF 神经网络算法模型对于跨介质飞行器水面弹跳运动参数快速预测,在保证预测准确性的基础上,能够显著提高参数预测时长效率达3~4 个数量级,近一步印证了本文研究的必要性。

表4 近似模型与有限元计算的效率对比Table 4 Calculation efficiency comparison between approximate model and finite element
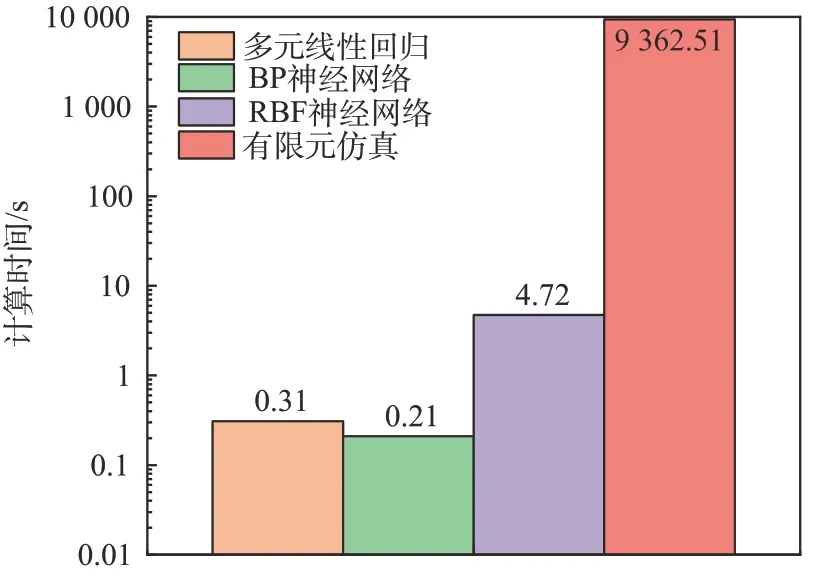
图13 快速预测模型与MPS计算时长对比Fig.13 Comparison of computational cost by rapid prediction models and MPS
5 结 论
针对跨介质飞行器水面弹跳运动参数的快速预测问题,本文基于线性多元回归、BP 神经网络和RBF 神经网络建立了不同的快速预测模型。通过对比分析研究,在保证近似精度和计算时长的同时,实现了跨介质飞行器水面弹跳运动参数的快速预测。得到如下结论:
(1)在跨介质飞行器水面弹跳运动速度预测中,线性多元回归模型和BP 神经网络模型对于水面弹跳运动的预测结果残差分别分布在±25 m/s、±30 m/s 内,其方差较大,平均相对误差分别为0.015与0.009,尤其对于速度较大时的弹跳运动的预测能力明显不足。基于RBF 神经网络模型建立的水面弹跳快速预测模型在样本空间上的误差均值为8.39%,残差主要分布在±15 m/s,R2为0.988,平均相对误差为0.007,近似性能最优。
(2)为近一步说明本文提出的跨介质飞行器水面弹跳运动参数快速预测方法的优势,对比3种快速预测模型与MPS数值仿真计算的计算效率,统计所需时间分别为0.31 s、0.21 s、4.72 s 与9362.51s,性能最优的RBF 神经网络快速预测相比数值仿真计算可缩短计算时长达3~4 个数量级。
本文研究了飞行器触水时的姿态及运动参数变化预测问题,后续可进一步考虑入水、出水时的姿态、运动参数的变化以及跨域控制相关研究,以进一步解决跨介质飞行器的跨域切换控制问题。此外,本文中方法能够对未来复杂变体跨域航行体多相耦合类运动高效切换总体设计提供一定的参考。

