基于激振扫描法对大型隔离器动刚度测试技术的研究
秦晓猛, 谭 棋, 卢 丹
(天津航天瑞莱科技有限公司成都分部, 四川 成都 610100)
0 引言
隔离器被广泛应用于减震类设备中,如在石油设备、舰船设备、大型电子柜和精密仪器等都设有各类型的减震器或隔离器。隔离器主要用于避免减缓振动冲击对关键设备的损坏,故对动刚度的特性要求极其严格。所以,大型动力设备中设有大型隔离器,其需要准确地了解其静态性能和动态性能,如动刚度、固有频率和损耗因子等。为了准确获取大型隔离器的动态特性,需要对其进行动刚度测试,目前,主要采用的方法有激振扫描法、自激振荡法和椭圆法。其中振动法具有激励频带范围广和操作简单的优势,但为了准确获取动态特性测试数据,需要对大型隔离器的振动工装进行设计,同时也需要具备激振扫描法的动刚度测试理论基础,才能保证数据获取的有效性。
1 激振扫描法动刚度理论
根据单自由度弹性系统中惯性力、阻尼力、弹性力及外力平衡原理,在假定弹性系统中为黏弹性结构阻尼,输入为简谐信号的条件下进行的[1]。当系统假定为结构阻尼、刚度为线性复刚度及输入为简谐力,在刚性基础情况下,M-K 弹性系统运动方程式为:
式中:M 为大型隔离器承受的额定配重,kg;K 为大型隔离器的动刚度,N/m;η 为系统结构阻尼的损耗因子;X 为配重的绝对位移,m;X¨为配重的绝对加速度,m/s2;F0为振动台激振力幅值,N;ω 为振动台激振圆频率,rad/s;t 为激振力加载的时间。
当式(1)中F0=0、台面位移为u=u0ejωt时为基础激励,力学模型如图1 所示,运动方程式转化为:

图1 激振扫描法力学模型
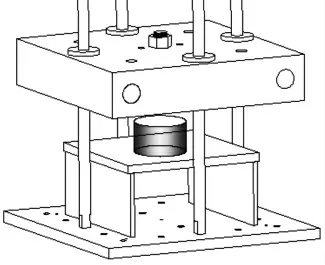
图2 激振扫描法动刚度测试工装示意图
求解方程(2),得到振动台激励的每个频率绝对位移响应幅值X0及绝对位移共振幅值X0,max分别由式(3)和式(4)表示。
当式(1)中F0=0,时,运动方程转化为:
求解该运动方程式(5),得到振动台激励的每个频率相对位移响应幅值δ0及相对位移共振幅值δ0,max,分别由式(6)和式(7)表示。
式中:u0为基础激振位移幅值;δ0为质量M 相对台面位移幅值,δ0=(X0-u0),m;为基础激振加速度幅值,m/s2;ωn为系统共振频率,rad/s。
当大型隔离器激振M-K 弹性系统位移共振时,激振力与阻尼力相等、惯性力与弹性力相等,于是动刚度可以按照式(8)计算:
2 激振扫描法动刚度测试方法
2.1 配重工装设计
激振扫描法是利用振动试验机对其施加位移或者加速度,所以需要对大型隔离器设计匹配的额定载荷工装。由于工装的稳定性会影响大型动刚度的测试结果,所以设计出符合满足测试要求的工装至关重要。
1)工装底部支撑结构在满足振动台能力的情况下,尽可能提高其刚度。
2)由于大型隔离器承重能力强而承重截面小,所以工装设计需要考虑其稳定性,可以考虑低阻尼辅助支撑或者采用多个隔离器共同进行测试。
3)工装自身的频率固有频率高,不会对整个系统产生影响。
2.2 测试程序
1)根据振动台的能力情况,激振力施加在振动台台面或系统质量上,激励频率通常从1/4~4 倍于被试系统共振频率的范围内进行正弦扫描或白噪声激振扫描,激振振幅参考表1[2]。

表1 激励振幅参考值
2)通过振动控制仪,记录振动台激励时台面输入和质量响应在各个振动台激励频率下的位移(或速度、加速度)值,并求解隔离器配重响应与激励之间的比值关系,得到无因次绝对位移响应曲线(亦称为传递曲线)。
3)若隔离器存在非线性动态特性,则应分别测出不同静载荷及位移幅值与动刚度(或固有频率)的关系曲线。激振振幅不变的情况下,改变静载荷进行测试;或在额定载荷下,改变激振幅值进行激振。
3 激振扫描法动刚度测试应用实例
3.1 测试布置
根据某大型船用隔离器的产品测试要求,采用激振扫描法,对其进行动刚度测试。试验件额定承载1 700kg,放置于振动试验机上,其测试布置如图3 所示。

图3 激振扫描法动刚度测试布置方案
3.2 测试计算
试验过程中,采用1g 的恒定加速度对其进行扫描激励,通过振动控制仪记录传递力及位移时域波形,并求解隔离器配重响应与激励之间的比值关系。以频率为X 轴横坐标、以传递比值为Y 轴纵坐标,绘制大型隔离器的无因次绝对位移响应曲线(亦称为传递曲线)。响应最大的时刻发生在隔离器固有频率处,则可以根据固有频率推算动刚度,如图4 所示。

图4 某隔离器激振扫描法主承载方向动刚度试验传递函数曲线
隔离器动刚度计算:
式中:fn为隔离器在额定配重下的固有频率,Hz;M 为隔离器额定配重质量,kg。
3.3 测试结果
隔离器动刚度测试结果,如表2 所示。

表2 隔离器动刚度测试结果
4 结语
大型隔离器动刚度测试是一项准确性要求极高的测试,实际测试过程中,需要根据试验件的实际情况合理设计工装,结合试验件特性合理选择激振量级,确保获取传递曲线有效准确,才能对其动态特性进行合理评估。综合来看,激振扫描法具有频带范围广、激励方便和易于计算的优势,但大型隔离器的承载要求高,在工装设计和对振动台的能力要求方面则是激振扫描法的劣势。

