超深富水基坑开挖工程突涌以及变形分析

高京生，程 乐，宗二凯，易德新

(1.宁波市轨道交通集团有限公司运营分公司,浙江 宁波 315000;2.宁波市轨道交通集团有限公司建设分公司,浙江 宁波 315000;3.宁波市轨道交通集团有限公司,浙江 宁波 315000; 4.宁波市市域铁路投资发展有限公司,浙江 宁波 315000)

0 引言

随着城市化进程的加速和土地资源利用的必然趋势,超深基坑已经成为建设高层建筑等工程的一种必要手段[1]。尤其是在一些城市中心区建设高层建筑时,常常需要建造数十甚至上百米深的超深基坑。在实际建造过程中,由于开挖深度较大,因此需要考虑地下水以及基坑周围环境的问题。针对基坑开挖问题,已有大量学者进行了研究[2]。在二元结构地层中赋存丰富的承压水的特定条件下,苏滔[3]系统研究软土二元结构深基坑降低承压水技术和应用;骆冠勇等[4]专注于探索承压水减压对土壤内应力和地表沉降的影响,并且在假设一维竖向固结的前提下,推导了减压引起的沉降固结度计算公式。杨毅秋[5]通过对工程实例的分析总结出微承压水对工程的危害,并借助PLAXIS有限元程序来分析承压水渗流条件下基坑工程的变形与稳定。为解决基坑支护和土体变形问题中承压水带来的难题,纪政[6]通过分析基坑变形形式与地下水理论,并模拟计算了承压水条件下支护结构的内力与土层变形。孙玉永等[7]通过数值模拟与理论分析,探讨三种承压水基坑突涌模式,并明确判定了基坑发生突涌的方法。王卫东等[8]首次在苏州地区采用超深TRD工法等厚度水泥土搅拌墙,并建立三维数值模型来模拟基坑开挖过程,经分析表明基坑开挖和降水均符合隧道要求。张飞等[9]对比了软土深基坑弹塑性数值模型与现有理论分析方法,验证了数值方法的合理性,此外还探讨了支护结构与坑底的变形规律。赵燕容等[10](2023)研究了广州新白云国际机场基坑降水工程,提出了基于抗突涌稳定性安全系数控制的基坑降水最优化模型;林必明[11](2023)等研究了上海市区基坑工程突涌发生的原因,介绍了具体的应对治理措施。

在宁波地区目前对于地铁深基坑的研究还不够充分,因此有必要深入探究该地区承压水的特性,以了解当地深基坑开挖对突发涌水及周边环境的影响。这样做可以为未来工程建设提供实践指导。基于此,笔者以宁波市轨道交通7号线明海大道站为例,采用PLAXIS 2D有限元软件建立基坑开挖模型,分析承压水基坑突涌稳定性,研究承压水条件下深基坑突涌水稳定性以及对周围环境的变形控制效果。

1 工程概况

明海大道站地处宁波市镇海区,为宁波市轨道交通7号线第24个站,车站设置于镇海大道上,呈东西向布置于规划路与镇海大道路口。镇海大道红线宽60 m,现状为双向八车道,车流量较大,两侧各有一条5 m 左右的人行道。规划路红线宽67 m。车站为地下2层岛式车站,为单柱双跨(局部双柱三跨)结构。该基坑深度为16.700 m,宽度为20 m。场地整平地面标高为3.300 m,地下连续墙深入地下43 m,墙厚0.8 m。基坑五道内支撑设置情况如表1所示,基坑开挖工序如表2所示。

根据工程性质和现场地质条件,场地地基土分析如下:①1a杂填土,①2黏土,③1b粉砂,③2粉质黏土,⑥2t砂质粉土,⑧1粉砂,⑧2粉质黏土。

根据本次钻探揭露地层情况,并结合区域水文地质资料分析,本场地勘探范围内埋藏分布有浅部孔隙承压水和深部孔隙承压水,其中深部孔隙承压水为第Ⅰ含水层组,其又分为Ⅰ1和Ⅰ2承压水。

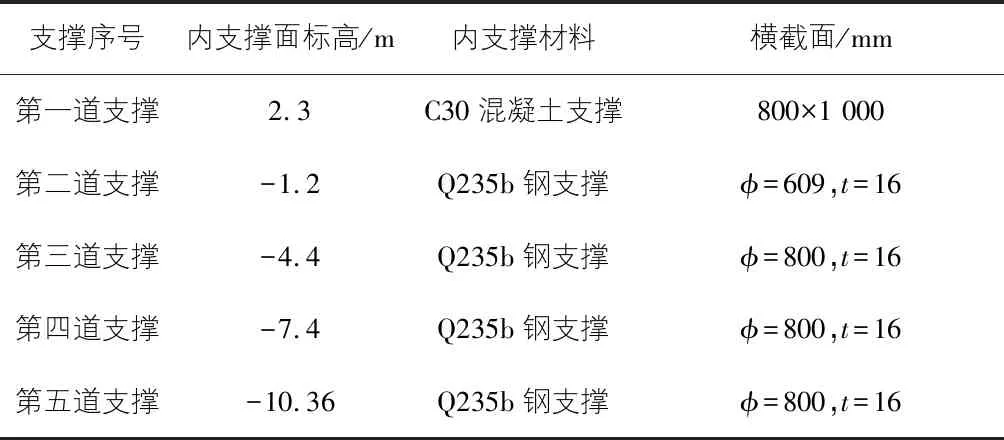
表1 基坑内支撑设置方式

表2 基坑开挖主要施工工序

1)浅层孔隙承压水主要赋存于③1b粉砂层中。根据区域地质资料及本次承压水头观测孔水头观测情况,其水位埋深一般在1.50 m～2.00 m左右,标高在0.8 m左右,渗透系数介于2.66×10-3cm/s～3.56×10-3cm/s左右,属中等透水,水量相对较小,单井出水量在34 m3/d～87 m3/d左右,补给和排泄均不畅,为封存式地下水,水质为咸水,地下水流速小。

2)Ⅰ1层孔隙承压水主要赋存于⑥2t层黏质粉土中。⑥2t层黏质粉土其顶板标高-42.52 m～-38.11 m,揭示层厚1.00 m～7.00 m,含水层透水性较好,根据详勘抽水试验成果,其测压水位埋深在2.15 m,标高为0.4 m,期间水头变化幅度较小,其平均渗透系数介于1.23×10-3cm/s～1.50×10-3cm/s之间,单井出水量34 m3/d～62 m3/d。

3)第Ⅰ2层孔隙承压水赋存于⑧1及⑧3a层粉砂中。根据区域水文资料及金华路站详勘抽水试验成果,渗透系数约1.95×10-3cm/s～2.52×10-3cm/s,属强透水,水量较丰富,单井开采量1 500 m3/d～1 800 m3/d,系市区地下水主要开采层之一,水温为19.5 ℃～20 ℃,静止水位埋深一般为2.70 m左右,高程-0.39左右。

2 基坑开挖有限元模型

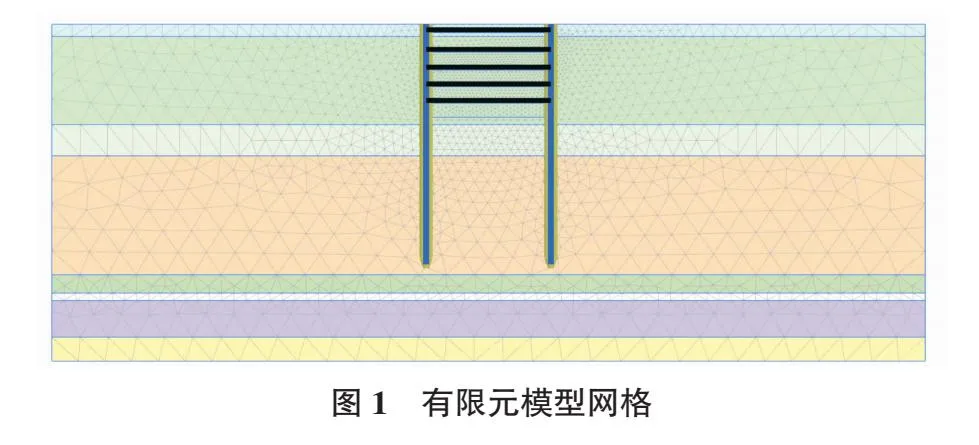
该工程基坑宽度为20 m。根据圣维南原理,基坑开挖影响区域为开挖尺寸的3倍～5倍,故确定模型尺寸为140 m×180 m(长×高)。采用PLAXIS 2D软件建立二维数值计算模型,通过模拟获得深基坑开挖过程中的变形结果。土层采用小应变土体硬化本构模型[12-13](Hardening Soil with Small-Strain Stiffness,简称为HSS模型)。土层参数由地质勘察报告和经验公式计算得出,表3列出了具体数据,小应变参数γ0.7统一取1×10-3。表4记录了地下连续墙和支撑材料的参数及模拟单元,土层与结构的界面强度折损参数按经验值取Rinter=0.67。为获得更准确的计算结果,划分为三角形网格,基坑内部粗糙系数设置为0.5,其余部分设置为1,采用超细的单元分布,共计5 798个单元和47 819个节点。数值计算网格划分详见图1。

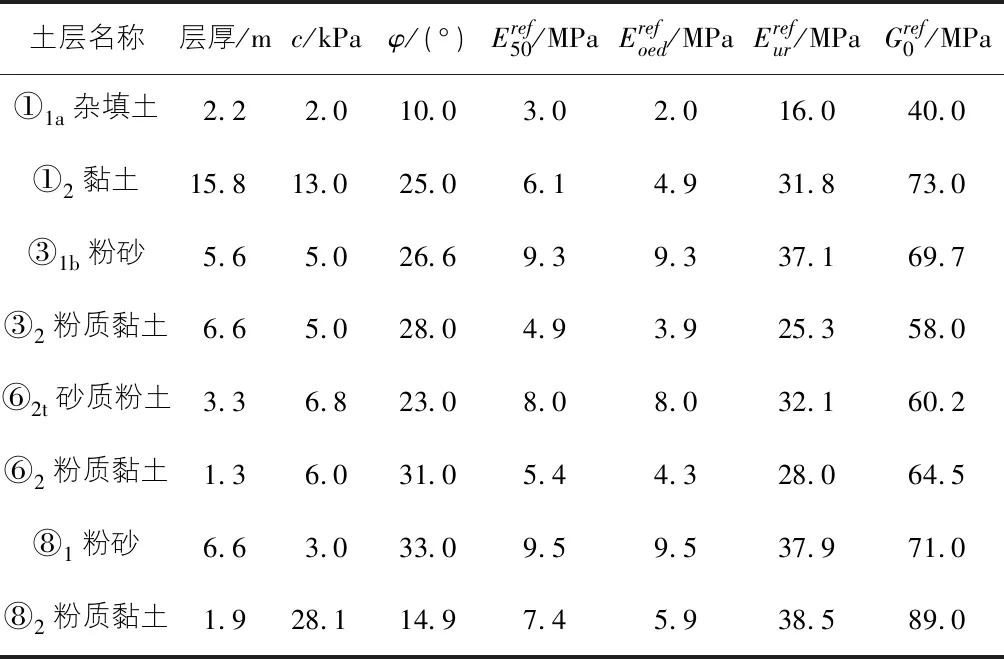
表3 HSS模型计算参数

表4 墙体及支撑材料参数

3 模型预测

3.1 基坑抗突涌验算

深基坑设计开挖面以下一定深度内埋藏有承压含水层时,必须进行基坑底板引起突涌的安全计算。要保证基坑的稳定,则基坑最终开挖面到下部承压含水层顶板间土的重量应大于承压含水层的顶托力[14]。

∑h×γs≥Fs×γw×H。

其中,h为承压含水层顶板与基坑最终开挖面之间的距离;H为承压水总水头;γs为承压含水层顶板以上土层的加权重度,kN/m3;γw为水的重度,取10 kN/m3;Fs为基坑抗突涌安全系数,本文中取1.10[15]。

地连墙底部位于⑥2粉质黏土中,已将③-1b层隔断,因此无需考虑该承压水层,只需考虑潜水和⑥2t砂质粉土层以及⑧1粉砂层承压水的影响。基坑抗突涌稳定性验算见表5。

表5 基坑抗突涌稳定性验算

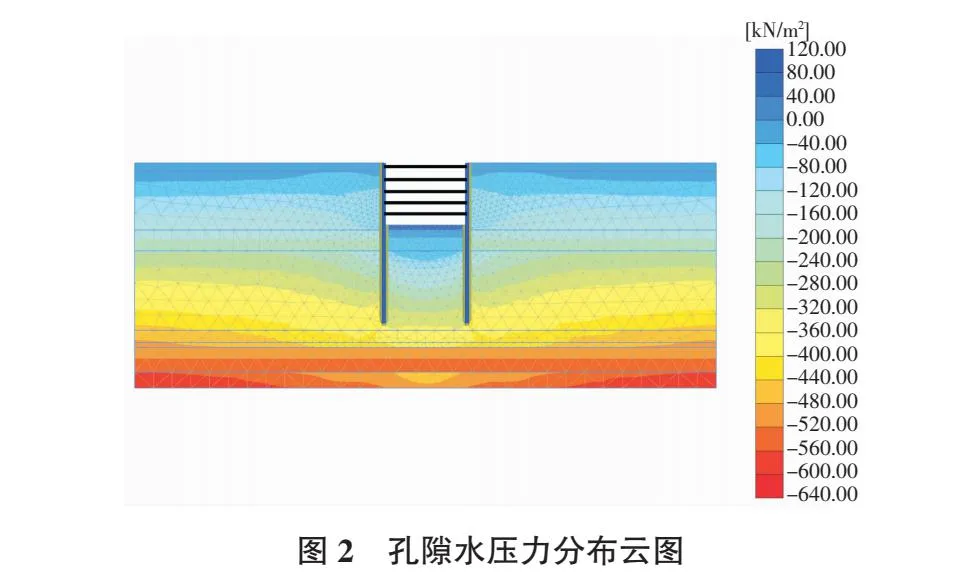
结合该基坑抗突涌水验算成果,模型模拟预测了基坑降水运行期间坑内外承压水稳定孔压,如图2所示。根据计算结果,⑥2t砂质粉土层以及⑧1粉砂层均符合突涌水的安全验算,说明该工程无需进行降承压水处理。

3.2 基坑外地表沉降

基坑开挖完成后地层总位移以及竖直方向上的位移云图如图3和图4所示,根据数值模拟计算,基坑外地面沉降量如图5所示。根据变化曲线可得,基坑周边地表沉降的变化规律均为先变大后变小,随着基坑施工工序的开展,该变化则更明显。开挖土层较浅的时候,随着离基坑的距离的增加,沉降的位移区别并不明显。当基坑开挖越来越深时,土层的沉降变化随着离开基坑的距离更为明显,沉降会迅速达到最大值。施工过程中沉降的最大值35.15 mm均出现在距离基坑20 m的位置。

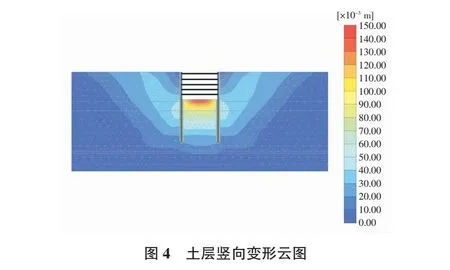
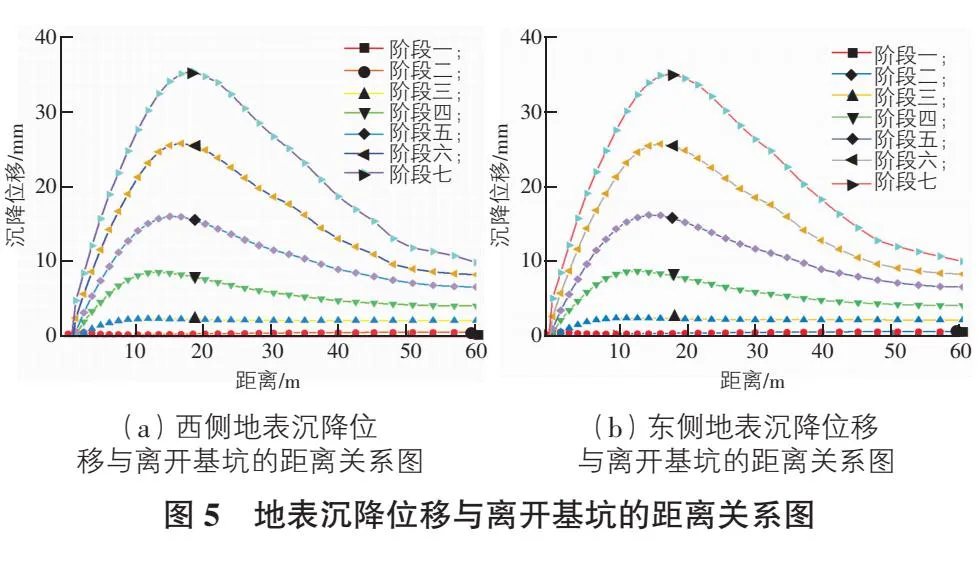
由图5可以看出,开挖富水条件下的超深基坑,距离基坑外60 m处地表沉降依然有10 mm左右。根据本工程的设计标准基坑标准段的基坑设计等级与环境保护等级分别为一级和二级,地面最大沉降量要小于0.2%H,代入基坑开挖深度16.7 m,计算得33.4 mm,数值模拟计算结果略大于该容许值,考虑与PLAXIS 2D建模过程中省略了冠梁存在较大关联。

根据王卫东等[16]的研究结论,最大地表沉降值介于0.1%H～0.8%H之间,最大地表沉降一般发生距离地下连续墙0.3%H～1.0%H,本工程最大地表沉降发生距离地下连续墙1.2H范围,与上海软土地区基坑开挖地表沉降规律略有不一致。

3.3 地下连续墙变形

基坑围护结构变形是施工质量的重要指标之一。在PLAXIS 2D中,分阶段进行施工计算,并得到各个施工工况下地下连续墙的水平变形见图6。在不同的施工阶段中,地下连续墙的最大变形位置发生了变化。同时,地下连续墙的水平变形呈现出“弓”形特征,即墙顶和墙底两端变形较小,而中间变形较大。这种特征与Zhang等[17]的研究结果相符。在软黏土中采用小应变硬化土模型本构进行有限元模拟,得到了围护墙体形成“肚鼓形”的类似结论。

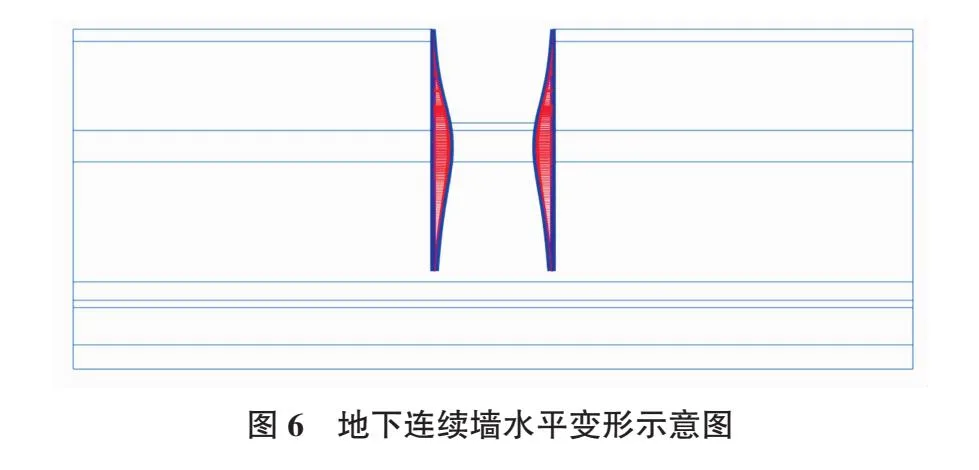
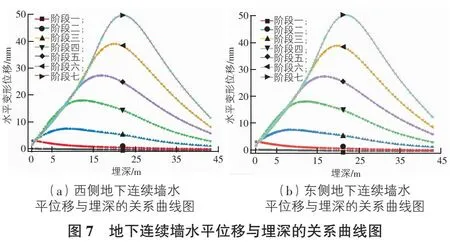
根据图7可知地下连续墙的最大水平位移值为49.8 mm,根据本工程的设计标准,围护墙最大水平位移为0.3%H,计算可得围护墙最大水平位移为50.1 mm,说明该工程的围护墙水平位移满足要求。

3.4 基坑底隆起位移及稳定性验算

随着基坑开挖进程,土壤平衡的应力场被破坏,卸载后基坑底部土体应力状态改变,产生回弹变形。本基坑工程基坑底部隆起位移如图8所示。基坑底部隆起位移最大的位置位于基坑中间,最大隆起位移为56 mm。

不同阶段基坑内土体的隆起变形如图9所示,对比不同阶段的基坑底土体隆起程度,结合基坑开挖深度,每个阶段的基坑开挖情况如表6所示。

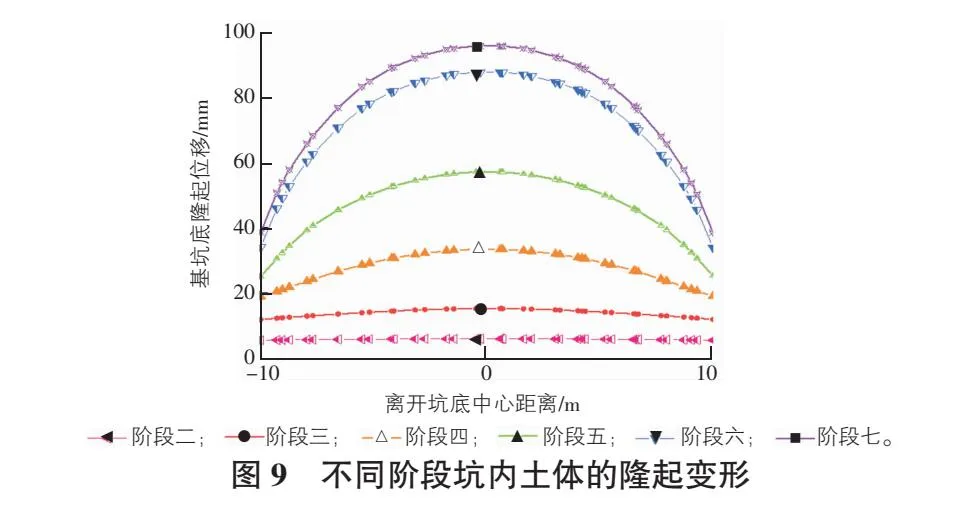
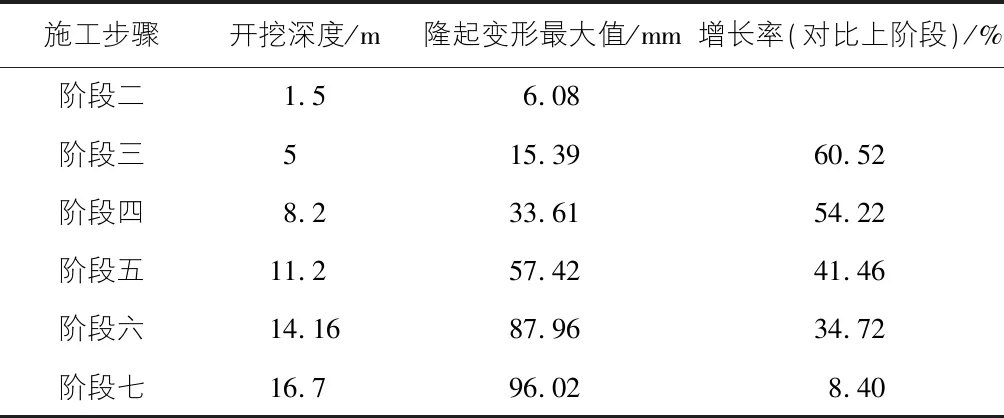
表6 各个阶段的基坑开挖情况

从不同阶段的增长率可以看出,随着基坑开挖施工进程,基坑底隆起位移不断增加,变形的增长率呈现下降的趋势,阶段七的变形增长率下降明显,这是因为该阶段开挖到基坑底部,浇筑200 mm厚C30早强混凝土垫层,将坑底变形控制在合适范围内。

基坑抗隆起验算是基坑工程设计的关键内容,关系到基坑支护、周边环境的安全以及基坑的变形。采用同时考虑c,φ的计算方法进行抗隆起稳定性验算。

其中,γ1为地表至地连墙底部土层的加权天然重度;γ2为坑底至地连墙底部土层的加权天然重度;Nq,Nc均为地基极限承载力系数;D为地下连续墙入土深度;H为基坑深度;q为地面荷载;c为地连墙底部黏聚力;φ为地连墙体底的内摩擦角。

根据普朗特尔公式可以得到地基极限承载力的计算系数为:

经计算,Ks=9.96,远大于本工程车站基坑稳定性设计标准1.8,符合要求。

4 地下连续墙深度参数研究

为研究地下连续墙深度对基坑抗突涌稳定性以及环境变形控制的影响,建立若干不同地下连续墙施工深度的计算模型。

4.1 地下连续墙水平位移变化

对比地下连续墙总埋深为43 m～53 m条件下的地下连续墙的水平变形,如图10所示。从图10中可以发现地下连续墙在总埋深从43 m增加至53 m时,地下连续墙的最大水平位移发生了极不明显的变化,并且地连墙深度的增加对最大值点位置的影响也并不明显。

4.2 基坑底土体隆起变形变化

对比地下连续墙总埋深为43 m～53 m条件下的基坑底的隆起变形,如图11所示,从图11中可以发现地下连续墙在总埋深从43 m增加至53 m时,基坑底土体隆起变形呈现出不断变小的趋势。地连墙埋深与坑底隆起最大位移情况如表7所示。

从降低率可以看出在一定范围内,增加地下连续墙的深度对坑底隆起位移并无明显作用。基坑隆起位移最大值均在基坑中间。

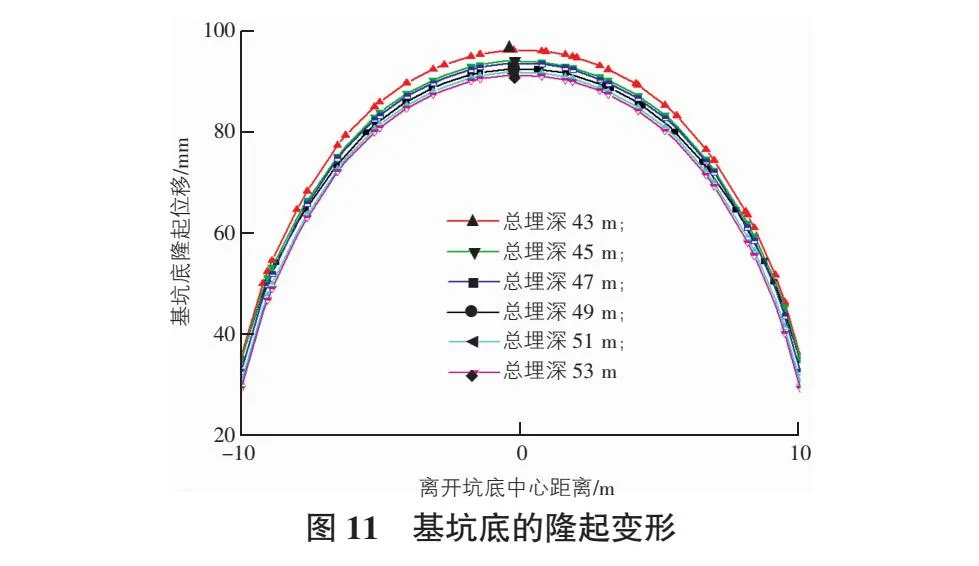
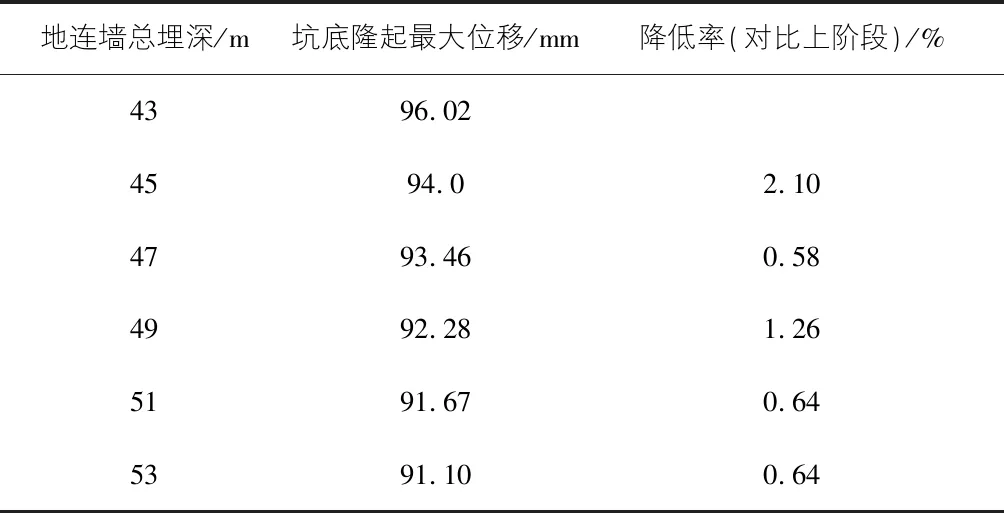
表7 地连墙埋深与坑底隆起最大位移情况表

5 结论

突涌水以及地表沉降特性会严重影响超深富水基坑开挖工程质量。本文通过计算基坑开挖过程中的抗突涌水系数、稳定性系数,以及基坑外地表沉降与地下连续墙水平变形,并进行了参数研究。研究结果如下:

1)运用数值模拟手段,采用HSS本构模型,模拟超深富水基坑开挖工程。经计算,地连墙水平变形值、坑底隆起变形小于容许值,表明该工程设计已能满足安全性考虑。

2)该模型能较好地分析基坑开挖过程中的变形规律。地连墙水平变形呈现出“弓”形特征;坑底隆起变形中间大两边小,变形增长率随基坑开挖施工进程而下降;坑外地表沉降最大值发生在距离基坑20 m的位置,随着基坑壁距离的增长,呈现出先变大后变小的特点。三者的变形规律符合现场实际与工程经验。

3)采用基坑底板引起突涌的安全计算以及同时考虑c,φ的计算方法,经理论分析及验算,基坑抗突涌与坑底稳定性均满足需求,说明现有施工方案已能保证该工程的安全,无需进行降承压水处理。

4)本文对地下连续墙的深度进行了参数研究,结果表明:基坑变形对地下连续墙入土深度并不敏感。因此,在宁波地区进行深基坑工程时,不建议采取增加地下连续墙深度的方式来控制变形。