高超声速非平衡流动-辐射特性数值模拟研究

杜耀文 孙素蓉 黄河激 孟 显 曹进文 耿金越 闫 聪 王海兴 ,

* (北京航空航天大学宇航学院,北京 102206)

† (中国科学院力学研究所,北京 100190)

引言

高超声速飞行器在飞行过程中面临极其严重的气动热问题.飞行器前方气体在很小的尺度内被压缩后形成的激波层内气体组分逐渐解离、电离,形成温度可达万度的高温气动热环境.高温气动热环境向飞行器传递大量热量,会引起飞行器表面材料烧蚀、对飞行器结构和载荷安全造成严重威胁,因而是当前高超声速飞行器设计和研制中需要考虑的首要问题[1-4].

高速飞行器承受的气动热流的构成十分复杂,由温度梯度所形成的对流热流,气体解离和电离组分在飞行器壁面复合所形成的化学热流以及激发能级退激所形成的辐射热流3 个部分组成.先前的研究发现,对于高空高速飞行状态,高温气体辐射现象对激波层内组分和能量输运有重要的影响,如阿波罗飞船再入时表面辐射热流可达总热流的30%[5],因此针对近地空间的高速飞行器设计和研制,发展合理的高温气体辐射计算模型,准确预测激波层高温空气的辐射及输运特性十分必要.

高超声速飞行器面临复杂的气动热环境,其中涉及重要的流动非平衡、热力学非平衡和化学非平衡行为,国内外学者基于气体动理学方法和流体方法对高温非平衡空气流动开展深入研究并取得了一定进展[6-11].符合物理实际的高温空气热化学动力学模型是准确预测激波层内气体状态、表面热流和辐射特性的基础.Park[12]、Gupta 等[13]和Dunn 等[14]发展出的高温空气总包模型(global model)是气动热数值计算中最常用的一类模型,总包模型将每种组分作为一个整体考虑而不区分其包含诸多能级的细节,这类模型的优点在于组分和反应较少,便于应用于多维CFD 模拟中.然而研究表明,在高空高马赫数条件下激波层内的激发能级分布会明显偏离玻尔兹曼分布[15],不同总包模型对于同一气动热问题的预测结果存在显著差异[16].因此,需要发展更加合理细致的碰撞辐射模型来研究气动热问题.碰撞辐射模型(collisional-radiative model,CR model)综合考虑各种组分的激发态及其相关的碰撞辐射过程,相比总包模型能够更细致地描述激波层内的物理过程,然而其复杂程度和计算难度也大大提升.目前大部分研究仍局限于零维模型的建立或者与一维流动耦合计算[17-20].Bultel 等[17]建立了考虑主要电子激发态的空气碰撞辐射模型,发现典型再入工况下的组分分布计算结果与经典总包模型的计算结果存在显著差异.Panesi 等[18]基于空气碰撞辐射模型对再入工况下的能级分布进行研究,发现在马赫数较高时电子激发态分布严重偏离玻尔兹曼分布,原因是高束缚态粒子会发生辐射和电离反应而被大量消耗.

高温气体辐射特性和输运计算对于预测高空高速流动气体的辐射热流至关重要.美国学者Park 开发了著名的非平衡空气辐射预测软件NEQAIR 85[21],随着NIST 数据库和国际合作项目The Opacity Project 对空气谱线数据库的更新,NEQAIR 辐射计算软件也相应地更新发展[22].NASA 开发了非平衡辐射预测程序LORAN[23],相比于NEQAIR,分子辐射的转动谱线结构被平滑拟合,可使吸收系数连续变化,大幅提高了计算效率.目前国内尚未有类似的非平衡辐射预测软件,迫切需要发展能够描述高温非平衡流场辐射特性及输运过程的数值计算模型及软件.

针对以上问题,基于典型高超声速飞行器FIRE II 的高温非平衡流场特性和辐射输运特性作为研究对象,首先建立了考虑详细电子激发态和振动态的高温空气碰撞辐射模型,并与一维激波后流动模型耦合计算激波后流动非平衡特性,主要包括热力学非平衡、化学非平衡和能级非平衡特性.在此基础上,耦合高温空气碰撞辐射模型、一维流动模型和逐线计算辐射输运模型,对激波后的高温气体辐射特性、辐射强度和辐射输运过程进行了研究,并深入比较分析不同飞行状态下辐射输运过程的差异.

1 数学物理模型

1.1 高温空气碰撞辐射模型

高温空气碰撞辐射模型将空气视为由N2与O2及其产物组成的混合气体,包括N2,O2和NO分子,N,O 原子,,,NO+,N+,O+离子以及电子11 组分.对于电子基态分子分别考虑了68 个振动态与47 个振动态,并考虑了分子和分子离子的电子激发态,这些分子电子激发态不区分其振动能级,考虑了N 原子的46 个电子激发态与O 原子的40 个电子激发态,对于原子离子N+和O+,仅考虑其电子基态.电子激发能级数据来源于NIST (National Institute of Standards and Technology)数据库.表1 详细列出了建立的高温空气碰撞辐射模型所包含的组分与能级,共包含248 个不同能级以及电子.

表1 碰撞辐射模型考虑的组分与能级Table 1 Species and energy levels involved in CR model

高温空气碰撞辐射模型详细考虑了粒子间发生的基本碰撞过程,包括电子或重粒子碰撞下的振动过程、分子的振动解离过程、分子电子激发过程、分子电离、原子电子激发和电离、激发态粒子之间的激发转移、带电粒子间的电荷交换、分子和原子间的中性交换等过程.对于重粒子之间的碰撞,其反应速率取决于平动温度Ttr,而有电子参与的碰撞则由电子温度Te控制.对于分子振动及解离过程,其速率系数采用局部复杂势模型[24]、SSH 理论[25]、准经典轨线方法[26]计算的理论计算结果;对于重粒子或电子碰撞下的电子激发、电离过程,本文采用了Lotz[27]和Drawin[28]提出的碰撞截面,并推导计算其速率系数;本文详细考虑了不同振动态的中性交换反应,并采用了Bose 等根据准经典轨线方法[29]计算的速率系数;对于原子之间的结合电离及其逆过程,其速率系数来自于试验测量[30-32],逆反应过程根据细致平衡原理,利用Boltzmann,Guldberg&Waage 和Saha 平衡常数计算得到逆向速率系数,该模型包含约40000 个正逆碰撞过程.高温空气碰撞辐射模型中的详细过程和速率选取见文献[20,33].

1.2 一维激波后流动模型

为了描述飞行器再入过程中驻点线上等离子体特征的演变,本文结合上述的高温空气碰撞辐射模型,建立了一维流动模型来模拟激波后流动,计算条件为FIRE II 再入试验1634,1643 和1648 s 轨迹点[34-35],具体来流情况见表2.图1 为激波后流动的一维示意图,本文的计算域为沿着x轴x ＞0 的区域,即激波后区域.将激波前缘(x=0)视为一个不连续界面,马赫数、压力、温度等参数在此处发生跃变,激波后的参数依据Rankine-Hugonint 关系式计算得到.

图1 激波后计算域Fig.1 Schematic diagram of computational region

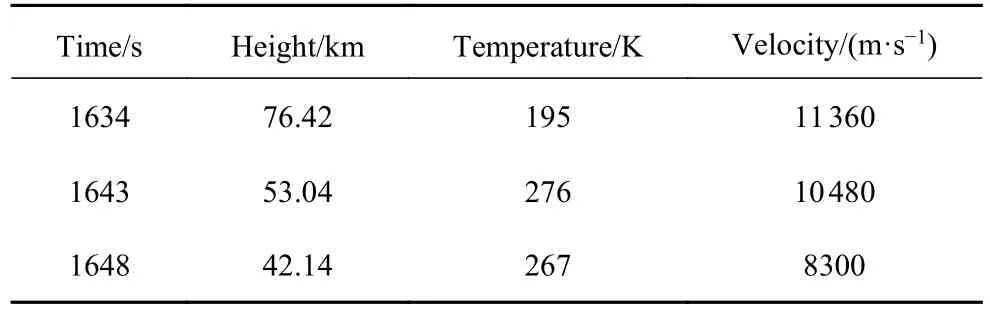
表2 FIRE II 飞行状态Table 2 Flight conditions of FIRE II vehicle

描述激波后流动的控制方程组如下.

组分连续性方程

式中,ρi为组分i的质量密度,u为气体流速,Mi为i粒子的质量,与分别为碰撞源项和辐射源项.

动量守恒方程

式中,ρ 为气体质量密度,p为气体压强,为重粒子分压pH和电子分压pe之和.

重粒子平动转动能量方程

式中,et,H为重粒子平动能,er,H为分子转动能,ρH为重粒子质量密度.QeH,elas为弹性碰撞项,QH,inelas为重粒子非弹性碰撞项.

电子能量方程

式中,ee为电子平动能,ρe为电子质量密度.Qe,inelas为电子非弹性碰撞项.

值得说明的是,本文通过详细振动态和电子激发态的独立组分连续性方程实现对振动能量和电子激发能量弛豫变化的求解计算,进而实现整个系统的能量守恒和方程封闭,因此无需单独求解振动能量方程和电子激发能量方程.

1.3 辐射输运模型

高温空气碰撞辐射模型考虑原子和分子的不同辐射跃迁机制,如图2 所示,模型包括N 和O 原子的束缚-束缚跃迁、束缚-自由跃迁和自由-自由跃迁,以及双原子分子N2,O2,N2+和NO 的束缚-束缚跃迁和束缚-自由跃迁,表3 给出了详细的辐射跃迁过程.

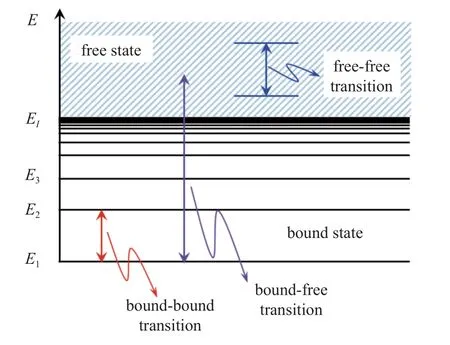
图2 辐射跃迁过程示意图Fig.2 Schematic diagram of radiative transitions

表3 碰撞辐射模型考虑的辐射跃迁过程Table 3 Radiative processes involved in CR model

对于原子束缚-束缚跃迁,考虑N 原子的1309 条谱线和O 原子的910 条谱线,谱线强度和跃迁几率等参数取自NIST 数据库[36],其发射系数计算考虑斯塔克展宽、自然展宽、压力展宽和多普勒展宽等多种展宽机制,并通过考虑非平衡效应的基尔霍夫定律[5]得到原子束缚-束缚跃迁的吸收系数.对于原子束缚-自由跃迁,通过TOPbase 数据库得到不同激发态粒子的光电离吸收截面,并由基尔霍夫定律得到其发射系数[37-38].原子自由-自由跃迁的发射系数和吸收系数计算通过对类氢原子的吸收截面修正公式得到[39].双原子分子束缚-束缚跃迁需要考虑分子内部的电子激发、振动和转动等不同激发能级之间的跃迁过程,其跃迁概率通过振动-电子激发跃迁矩和转动线强函数的乘积获得,并结合普朗克函数获得其跃迁发射和吸收系数.分子束缚-自由跃迁考虑分子的光电离、光解离等过程,基于吸收截面获得其吸收系数和发射系数[40-43].

本文在获得气体辐射发射和吸收系数基础上求解辐射输运方程

其中Iλ为波长 λ 下的辐射强度,ελ为发射系数,κλ为吸收系数.

如图3 所示,本文采用球帽近似假设计算沿飞行器一维驻点线的辐射输运[44],将球立体角离散为π/18的单元,并将70～ 6200 nm 的波长范围等间隔分割为613001 个波长点,空间离散与流场网格一致.

图3 球帽近似模型Fig.3 The spherical cap model

2 模型有效性验证

本文首先将高温空气碰撞辐射模型计算结果与Cruden[45]测量得到的电子数密度进行比较以验证碰撞辐射模型的有效性.Cruden 通过高分辨率光谱测量了激波管中激波后的电子数密度.如图4 所示,本文通过一维激波后流动模型与高温空气碰撞辐射模型的耦合计算,获得相同压力、速度条件下的激波后平衡区电子数密度,图4 为计算结果与测量结果的比较,随着来流速度和压力的增加,实验测定的电子数密度也逐渐增加,图4 表明高温空气碰撞辐射模型计算结果与实验测量结果符合良好,证明本文建立的高温空气碰撞辐射模型的有效性.

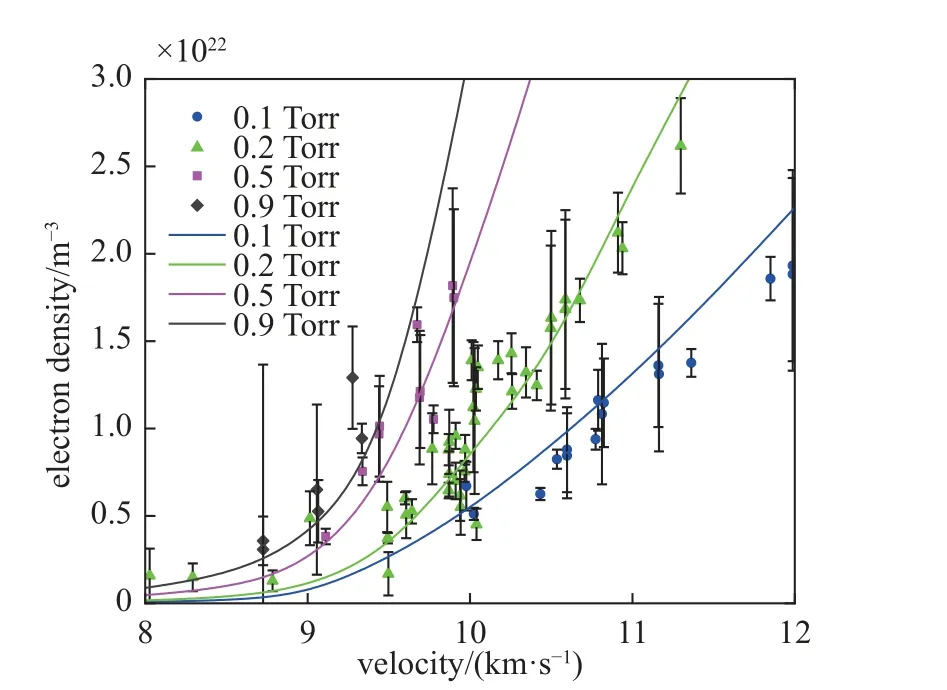
图4 计算结果(线)与Cruden 测量(点)[45]得到的电子数密度结果比较Fig.4 Comparison of the calculated electron density (lines) with experimental data (points)[45]

本文采用平板基准模型评估高温空气辐射输运模型的有效性,如图5 所示,模型包含两层分别处于15000 K 和8000 K 条件下的平衡空气,分别近似代表再入飞行器驻点线上的无黏区和边界层区域.将计算得到不同出口处的累积辐射热流与Chauveau等[41]计算结果进行比较,在两层平板出口得到的辐射热流分布与文献取得良好的一致性,证明了当前高温空气辐射输运程序的有效性.

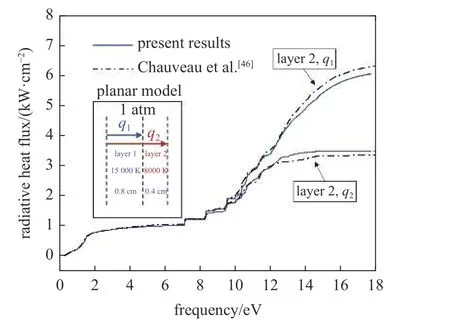
图5 平板模型累积辐射通量分布与文献[46]比较Fig.5 Comparison of the calculated radiative flux (solid lines) with Ref.[46] (dot dash lines)

本文对流动、碰撞反应和辐射输运耦合模型进行了综合验证,如图6 所示,图中飞行数据为FIRE II飞行试验通过光谱辐射计测得驻点位置处的频率范围2.2～ 4.1 eV 的积分辐射强度[34].为了与飞行器驻点辐射试验数据进行比较,本文首先估算FIRE II 不同轨迹点的激波脱体距离,通过Zander 等[46]的试验数据插值可以得到3 个轨迹点的激波脱体距离均为4 cm 左右.本文计算获得激波后该距离处的频率范围2.2～ 4.1 eV 积分辐射强度,并与飞行试验数据进行比较,图6 表明计算结果与飞行试验数据具有良好的一致性,有效验证了流动、碰撞反应和辐射输运耦合模型的准确性.

图6 FIRE II 驻点处2.2～ 4.1 eV 积分辐射强度与飞行试验数据比较Fig.6 Comparison of the stagnation point frequency-integrated radiative intensity with the flight data

3 流动非平衡特性

飞行器表面的气动热流和辐射热流与激波层内流动的热化学非平衡特性密切相关,具体而言: 特征温度分布会影响对流热流,化学组分分布会影响组分扩散热流,而电子激发能级分布影响辐射热流结果,因此有必要对激波层内热化学非平衡特性进行深入的分析研究.

3.1 热力学非平衡特性

图7(a)为计算得到的FIRE II 1634 s 轨迹点激波后的特征温度演变.其中平动温度Ttr和电子温度Te分别由各自能量方程得出,振动温度Tvib根据振动分布推导得出,根据下式计算

图7 激波后特征温度演变Fig.7 The spatial evolution of characteristic temperatures behind the shock front

式中,Ev为v能级振动能量,[N2(X,v)]为v能级的数密度.

从图中可见,在激波后,重粒子平动温度可高达62600 K,而电子温度和振动温度仍然非常低,Tvib-N2和Tvib-O2在1.0 × 10-6m 处开始上升并在4.0 × 10-4m和6.0 × 10-4m 处达到峰值,同时可以观察到平动温度的大幅度下降.在振动温度达到峰值之后,Ttr和Tvib经历了明显的下降,这是因为在这一阶段分子大量解离造成的能量损失.其后,由于原子碰撞振动激发过程转移能量至振动模态,振动温度又逐渐上升,在电子碰撞振动退激过程的作用下,电子温度在4×10-4m 处开始上升,并逐渐与振动温度达到一致,最终在激波后2.0 × 10-2m 处与Ttr达到平衡,平衡温度可达10490 K.这表明等离子体在距离激波前缘2 cm 处达到了热力学平衡,热力学非平衡区厚度与激波层厚度相当,在这种情况下,热力学非平衡效应非常强烈,在气动热模拟中必须加以考虑.

图7 同时比较了FIRE II 1634,1643 和1648 s 轨迹点激波后流动的特征温度演变,表明不同飞行高度和马赫数下,激波后流动的温度参数和非平衡效应存在显著差异,相比于1634 s 轨迹点,1643 s 和1648 s 轨迹点的来流速度有所降低,使得激波后平动温度下降,同时由于高度下降,气体密度更高,加剧了高温空气内的粒子碰撞和能量交换,因此其热力学非平衡区域要远远小于1634 s,热力学非平衡效应不明显.

3.2 化学非平衡特性

图8(a)为FIRE II 1634 s 条件下高温空气总包组分在激波后的空间演变过程.可以看出,在激波后发生中性交换反应,产生NO 组分.随后N2,O2,NO 数密度大幅下降,N,O 数密度增加,这一阶段主要发生解离反应,并且由于O2解离能(5.2 eV)远低于N2解离能(9.7 eV),O 原子要先于N 原子产生,在4.0 × 10-4m 处原子成为流场的主要组分.电子从4.0×10-4m 处开始急剧升高,前期主要依赖于重粒子温度控制的结合电离反应,直至电子数密度与电子温度都已足够高时,电子碰撞原子电离成为主要途径,主导离子为N+与O+.在3.0 × 10-2m 处,总包组分数密度不再发生变化,最终达到化学平衡状态.

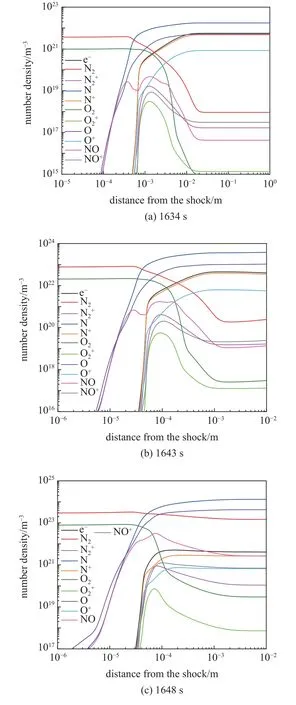
图8 激波后总包化学组分演变Fig.8 The spatial evolution of chemical components

图8 同时比较了FIRE II 1634,1643 和1648 s 轨迹点激波后流动的化学演变过程,相比于1634 s 轨迹点,1643 s 和1648 s 轨迹点的化学反应发生更为迅速,化学非平衡空间尺度为1 × 10-3m 量级,其达到平衡后解离和电离程度要更低.

3.3 能级非平衡特性

图9 为FIRE II 1634 s 条件下激波后激发能级分布特征.图9(a)为氮相关的振动态粒子与电子激发态粒子在激波后的空间演变过程,可以看出,在1 × 10-4m 前主要是振动态粒子的增加,这一阶段主要是分子碰撞振动激发过程(VTm)、原子碰撞振动激发过程(VTa)和振动交换过程(VV)导致振动激发,当振动态积累到一定程度时,解离过程开(始发)生,可以看到从1×10-4m处开始,基态原子快速增加,而振动态分子数密度急剧下降.分子离子、原子离子和电子激发态粒子的数密度在5 × 10-4m 位置处急剧增加,这一阶段主要发生电子激发与电离反应.在2 × 10-2m 处,各粒子组分达到平衡,可以看到此时电子激发态原子占有很大的比重.

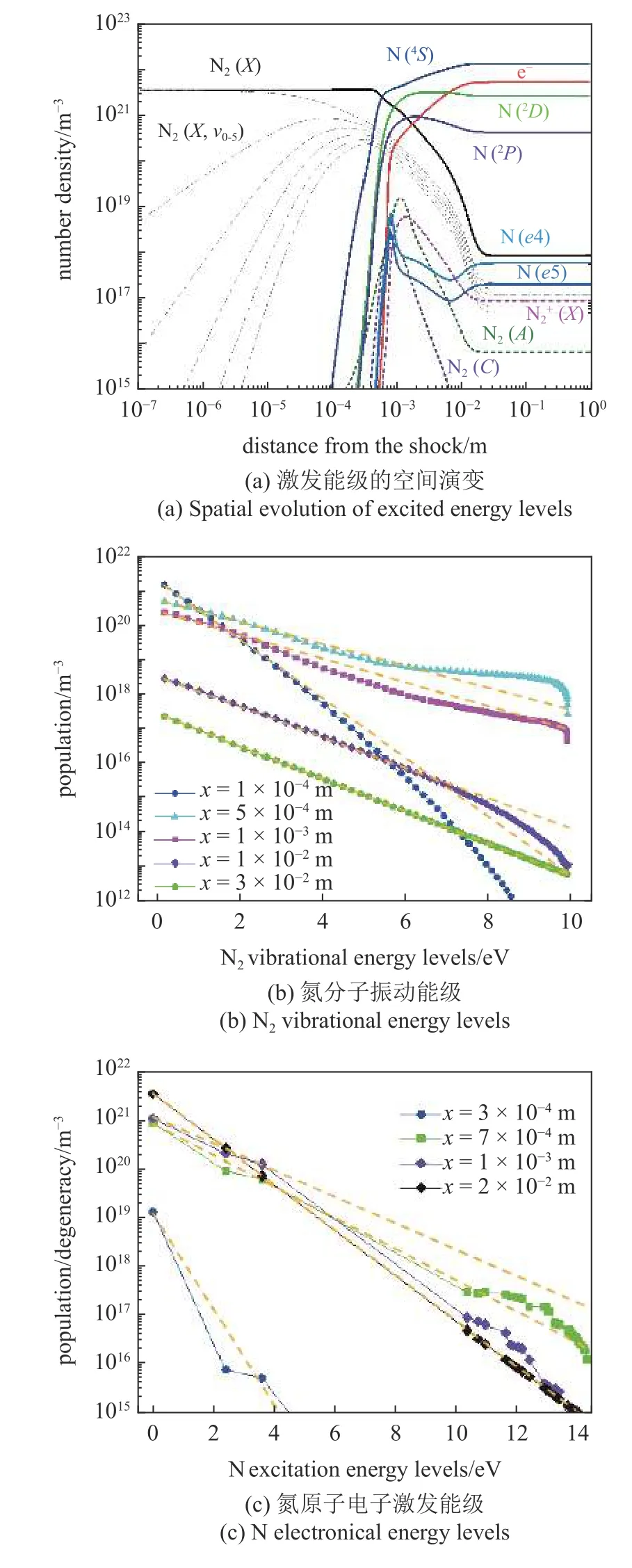
图9 激波后激发能级分布Fig.9 Distribution of energy levels behind the shock

图9(b)为激波后不同位置处的氮分子振动能级分布,可以看到在1.0 × 10-4,5.0 × 10-4,1.0 × 10-3和1.0 × 10-2m 处,振动能级分布明显偏离玻尔兹曼分布(图中橙色划线),高振动能级远低于平衡态,这与高振动能级解离速率过快导致的消耗有关,而在3.0 × 10-2m 处氮分子振动能级遵循玻尔兹曼分布,达到能级平衡状态.图9(c)为激波后不同位置处的氮原子电子激发能级分布,在3.0 × 10-4,7.0 × 10-4和1.0 × 10-3m 处,电子激发能级的高束缚态远低于玻尔兹曼分布,这与其快速电离反应密切相关,而在2.0 × 10-2m 处氮原子电子激发能级遵循玻尔兹曼分布,达到能级平衡状态.

由此可见,高振动能级和高电子激发能级在激波后一段距离内并不满足玻尔兹曼分布,其空间尺度可达1.0 × 10-2m,因此能级非平衡效应在高超声速流动中同样十分突出,而能级非平衡效应对能量弛豫、化学反应和辐射预示有至关重要的影响.

4 辐射特性与辐射输运

将高温空气碰撞辐射模型与流动方程耦合求解获得激波后的热化学参数和能级分布,在此基础上结合辐射输运模型可以求解获得高温空气的辐射系数、辐射强度和辐射输运通量.

4.1 高温空气辐射系数

图10 为FIRE II 1634 s 距离激波2.5 cm 位置处的高温空气发射系数和吸收系数的分布.可以看到原子束缚-束缚谱线可以分为两组,一组位于红外和可见光波段,其主要与高束缚能级之间的辐射跃迁有关,另一组位于真空紫外波段,具有极高的发射和吸收系数,其主要与发生在高束缚能级和基态、亚稳态能级之间的跃迁有关.原子束缚-自由跃迁主要处于真空紫外波段,而原子自由-自由跃迁,即韧致辐射主要处于低能红外区域.相比于原子的辐射跃迁过程,分子谱带的辐射系数相对较低,其中N2的第一正带和第二正带、的第一负带的贡献相对较大.

4.2 激波后辐射强度分布

图11 为不同飞行状态下激波后辐射强度随空间位置和光子频率的分布情况.从FIRE II 1634 s 条件下激波后辐射强度分布可以看到不同波段随空间的演变规律存在差异,真空紫外辐射(hv＞ 6.2 eV)的辐射强度在激波后非平衡区域内有很明显的辐射吸收,而其他波段的辐射强度在激波后持续增加并最终达到稳定,其辐射吸收效应相对较弱.真空紫外辐射具有较高的辐射强度,在非平衡区域可达106W/(cm2·μm-1·sr-1)量级,在平衡区域的辐射强度可达104W/(cm2·μm-1·sr-1)量级,真空紫外辐射主要与第二组原子谱线发射有关,与图10 中原子谱线的高辐射发射系数相对应.红外波段的辐射强度也相对较大,可达103W/(cm2·μm-1·sr-1)量级,其主要与低能原子束缚-束缚跃迁有关.

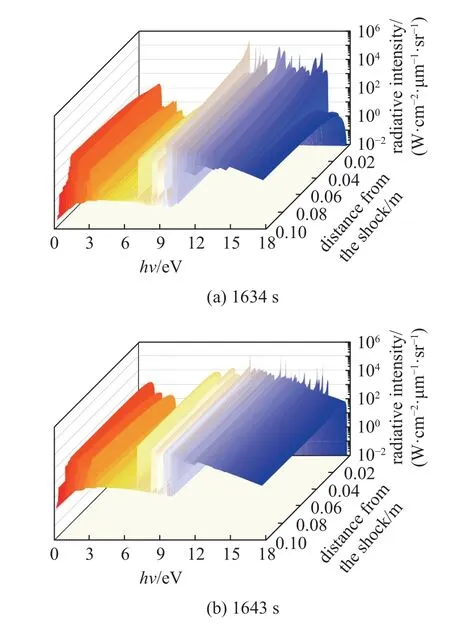
图11 激波后辐射强度分布Fig.11 Distribution of radiative intensity

相比于1634 s 条件,1643 s 条件下真空紫外波段的辐射强度有所降低,非平衡区域真空紫外谱线强度为104W/(cm2·μm-1·sr-1)量级,而在平衡区域真空紫外谱线强度为103W/(cm2·μm-1·sr-1)量级.而1648 s 条件下真空紫外辐射强度进一步下降至102W/(cm2·μm-1·sr-1)量级,表明随着高度和马赫数的下降,高能原子谱线造成的真空紫外辐射对总辐射输运的贡献逐渐下降,而分子谱带造成的红外、可见和紫外波段辐射的贡献逐渐增加.

4.3 激波后辐射输运过程

图12 为不同飞行状态下从激波向波后的辐射输运通量.从图中可以看到FIRE II 1634 s 在激波后非平衡区域内存在很明显的辐射吸收效应,这与激波后非平衡阶段高电子激发能级的快速电离反应有关,正如第3 节所述,电离反应导致了高能级的快速消耗和电子温度下降,因而使得气体发射系数减小而吸收系数增加,表现出强烈的吸收效应,平衡区域真空紫外和红外辐射通量持续增加,这主要与原子束缚-束缚跃迁有关.本文截取激波后4 cm 处的辐射通量作为飞行器表面辐射热流的参考值,1634 s条件下激波后4 cm 处辐射通量为66 W/cm2,其中真空紫外辐射通量为49 W/cm2,为总辐射通量的74.2%,而红外辐射通量为14 W/cm2,为总辐射通量的21.2%.

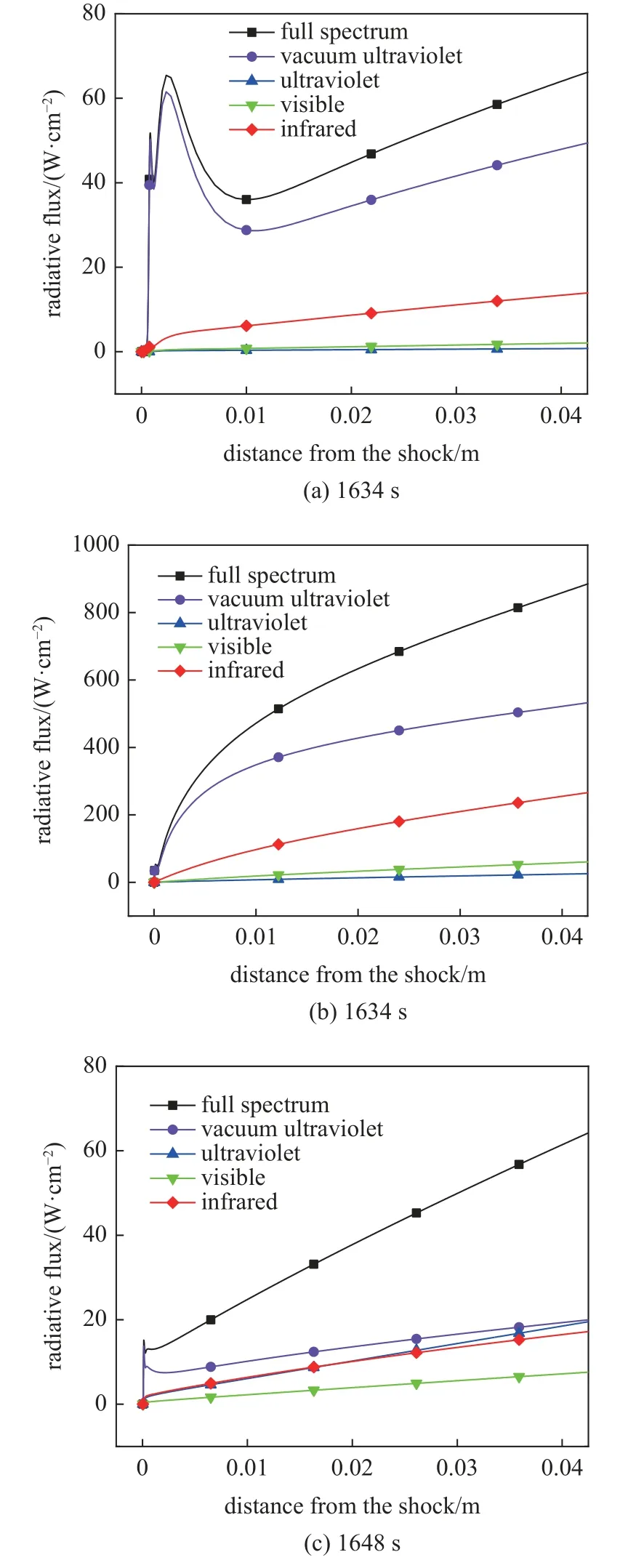
图12 激波后辐射输运通量Fig.12 Radiative transfer fluxes behind the shock front

对于FIRE II 1643 s 条件下的辐射输运,由于其激波后流动非平衡程度较低,因此其波后辐射吸收效应较弱,在激波后总辐射通量、真空紫外辐射通量和红外辐射通量持续增长,在激波后4 cm 处,总辐射通量可达887 W/cm2,其中真空紫外辐射通量为526 W/cm2,为总辐射通量的59.3%,红外辐射通量为263 W/cm2,为总辐射通量的29.7%.而对于1648 s 条件下的辐射输运,激波后辐射通量持续增加,其中真空紫外、紫外、可见光和红外辐射都有相当大比例的贡献,在激波后4 cm 处,总辐射通量可达64 W/cm2,其中真空紫外辐射通量为20 W/cm2,为总辐射通量的31.2%,紫外辐射通量为20 W/cm2,为总辐射通量的31.2%,可见光辐射通量为7 W/cm2,为总辐射通量的10.9%,红外辐射通量为17 W/cm2,为总辐射通量的26.6%.

对比不同飞行状态的辐射通量可以发现,随着高度下降和速度降低,真空紫外辐射通量在总辐射中占据的比例逐渐下降,而其他波段,包括红外、可见光和紫外辐射的比例逐渐增加,这是由于气体解离和电离程度下降,原子谱线对辐射输运的贡献逐渐降低,而分子谱带的贡献逐渐增加,依据图10 中的辐射系数分布,原子谱线主要分布于真空紫外波段,这使得真空紫外的辐射输运逐渐下降.

5 结论

本文发展了具有非玻尔兹曼电子能级分布和振动能级分布的高温空气碰撞辐射模型,耦合一维激波后流动方程计算不同飞行条件下激波后的非平衡流动特性,采用逐线计算辐射输运模型获得激波后非平衡辐射特性、辐射强度和辐射输运过程,深入比较分析了不同飞行高度和马赫数对非平衡流动和辐射输运过程的影响.

计算获得了FIRE II 飞行器不同轨迹点的波后热化学参数,结果表明对于高空高马赫飞行条件,其波后流动存在显著的热力学非平衡、化学非平衡和能级非平衡特征,在近激波区域,由于高振动能级的快速解离反应,其密度远低于玻尔兹曼分布,此外原子的高束缚电子激发态同样出现了明显的欠分布.

采用逐线积分方法对激波后非平衡辐射输运过程进行计算分析,结果表明在高空高马赫条件下真空紫外辐射占据主导地位,其主要由高能原子束缚-束缚跃迁造成,此外低能原子谱线造成的红外辐射也有较大贡献.随着高度和马赫数的下降,激波层内气体解离和电离程度降低,原子辐射贡献下降,分子辐射贡献增加,这导致红外、可见光和紫外波段的辐射输运增强,真空紫外辐射输运过程减弱.