经纬仪最佳一致逼近多项式速度实时求解

赵立荣，袁光福，吴 冬，高 群，王潇洵

（1.中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033；2.中国人民解放军95859部队，甘肃 酒泉 735000）

1 引言

光电经纬仪广泛用于火箭、导弹和无人机等飞行目标的外弹道/航迹参数测量，是靶场主测设备之一，主要进行目标极坐标测量即方位角、高低角。测量目标速度的应用相对较少，武器实验靶场一般采用连续波脉冲雷达的多普勒效应来实现对被试目标的速度进行测量，该方法可以获得较高的速度测量精度。随着数据拟合、滤波等数据处理技术的发展，对空中目标进行测速的应用越来越多。带激光测距的经纬仪系统通过对空中目标进行光学侦察以获取目标相对于地面站的方位和俯仰信息；然后，利用激光测距获取目标的距离信息，对目标进行空间定位；最后，通过多次定位数据和定位时间间隔，计算得到目标的飞行速度。经纬仪获得的位置信息在时间序列上是离散的，在对毫秒级采样间隔时间差分求速度时，经纬仪位置上一点小的误差，会造成很大的速度误差，因此对测量数据的滤波、拟合、平滑及外推是实时高精度获得速度信息的关键［1-5］。

王冰等人在文献［6］中提出经纬仪单站测量速度，通过多次定位数据和定位时间间隔，计算得到目标的飞行速度。飞行速度49～56 m/s，误差为3%～16%，此方法最小速度误差为1.47 m/s，误差较大。

应用在经纬仪上拟合目标运动轨迹求速度的方法，大多采用最小二乘法，最小二乘法是根据均方根误差最小的原理得到目标的运动轨迹求速度。对于做复杂运动，且速度较快的目标来说，要达到较高的拟合精度，拟和函数的阶次较高，计算量大，实时性不好。三次样条函数插值求速度，具有二阶光滑度和良好的收敛性，但是没有对三阶毛刺误差进行处理，在实际测量速度时，会存在毛刺误差［7-8］。

文献［9］提出一种基于雷达和光学经纬仪合理布站优化组合测量与数学计算求取弹丸速度参数的方法，采用三次Hermite 函数表示，优点是计算精度稳定，缺点误差大。

多年靶场外测数据处理工作的实践表明，即使是高精度的测量设备，也会因为多种偶然因素的影响，采样数据集合中往往包含0.1%～0.2%的严重偏离目标真值的异常数据［10］。工程领域称这部分异常数据为野值。野值对目标测量速度有十分不利的影响，需要采用有效的方法进行剔除。

利用经纬仪测量目标速度，通常获得目标位置，然后通过差分获得目标速度，比较典型的求解方法有高斯函数方法及卡尔曼方法。高斯函数方法求解速度实时性好，但测量速度精度不高；卡尔曼方法求速度精度很好，但是因为用了大量的历史数据，速度值产生滞后。只有提高速度的实时性、高精度才能满足靶场上导弹、飞机等多种目标测速要求。

本文采用最佳一致逼近多项式的方法对测量速度进行拟合、平滑及外推，保证了速度的实时性；采用了有限差分的方法识别速度的野值，去除野值，确定去除野值阈值，利用迭代的方法，获得最优速度值。本文方法既保证了目标测量速度的实时性，又保证了目标测量速度精度，在实际经纬仪加装激光测距系统中，取得了很好的效果。

2 测速工作原理

2.1 位置测量

单站光电经纬仪通过加装激光测站仪，获得目标三个测量元素：距离R、方位角A及俯仰角E。以经纬仪中心点OC为原点，Xc轴方向为大地北，建立OC(XC，YC，ZC)坐标系，如图1 所示。

图1 单站定位原理示意图Fig.1 Schematic diagram of single station positioning principle

单站定位公式如式（1）所示：

2.2 最小二乘方法剔除激光测距距离野值

经纬仪激光测距机测得的距离首先进行拟合剔除野值，再与方位角、高低角计算位置，从而计算的速度才能更精确。最小二乘法实时性不好，采用数据外推的方式改进最小二乘法，提高距离实时性［11］。

最小二乘法数据处理方法如下：

确定t个测量的参数X1，X2，…，Xt的估计量x1，x2，…，xt，测量值Y，存在t个未知值与Y是函数关系，n次测量Y值，获得l1，l2，…，ln数据，有关系式如式（2）所示：

设Y1，Y2，…，Yn的估计值为y1，y2，…，yn，则关系式如式（3）所示：

而l1，l2，…，ln的残余误差公式如式（4）和式（5）所示：

式（4）和式（5）为残余误差方程式。

若数据l1，l2，…，ln的测量误差是服从正态分布，设定标准差为σ1，σ2，…，σn，则各测量结果l1，l2，…，ln出现于真值附近dδ1，dδ2，…，dδn区域内的概率为：

根据最大或然原理，可认为这n个测量值同时出现于相应区间dδ1，dδ2，…，dδn时概率最大，应满足：

结果为估计量，以残余误差的形式表示，即：

式（8）存在平方量，求解困难，可以把其线性化。利用级数展开把式（8）非线性形式线性地表达出来：

相应的外推估计量为：

其误差方程为：

最后根据误差最小拟合曲线，求解平滑后的距离值。此方法的精度取决于误差阈值，设定误差越小，精度越高，计算量越大。

2.3 目标测速模型建立

利用激光测距获取目标的距离信息，对目标进行空间定位，通过拟合获得准确的弹道位置数据，定位时间间隔已知，计算得到目标的飞行速度［6］。如图2 所示，以经纬仪中心点OC为原点，Xc轴方向 为大地 北，建 立OC(XC，YC，ZC)坐 标系，设在t1和t2时刻目标从P1飞到P2，线速度为v，两点相对于OC点的坐 标分别 为P1(A1，E1，R1，t1)和P2(A2，E2，R2，t2)，A1、E1、R1为P1点对应的方位角、俯仰角及目标截距，同理A2，E2，R2为P2点对应 的方位 角、俯仰角 及目标截距；P1'和P2'为P1点和P2点在 地面的投 影。

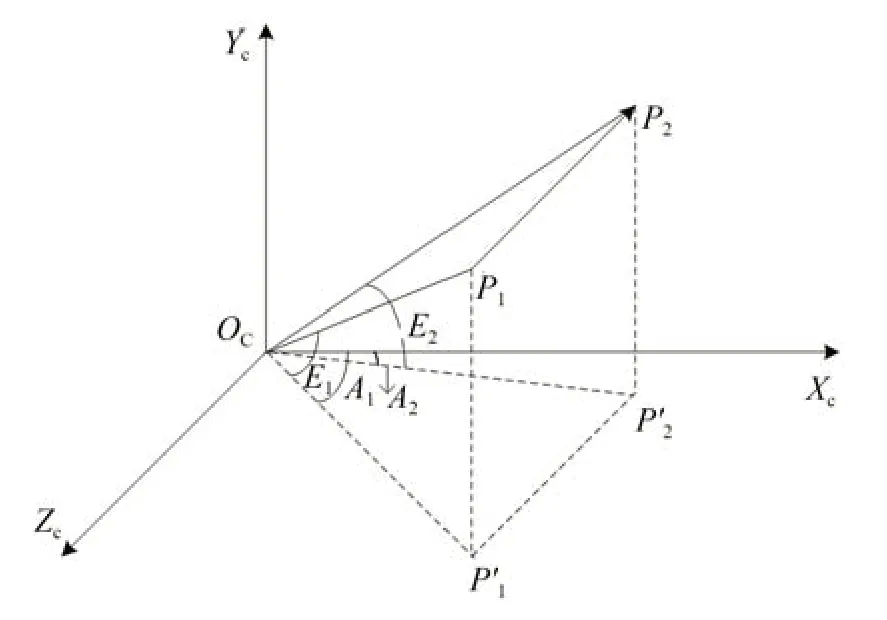
图2 目标测速示意图Fig.2 Schematic diagram of target velocity measurement

根据图2 的几何关系可以推出目标从P1飞到P2位移如式（12）所示：

目标速度公式如式（13）所示：

由速度测量公式（13）可知，目标速度v是一个与目标截距、方位角及俯仰角等参数有关的函数，可以表示为v(A1，A2，E1，E2，R1，R2)。其引起误差的原因有：（1）光测设备激光测距在P1点和P2点的激光测距误差δ(R1)，δ(R2)；（2）光测设备目标在在P1点和P2点测角误差δ(A1)，δ(A2)，δ(E1)及δ(E2)。

速度的误差公式可表示为：

3 速度求解

3.1 最佳一致逼近多项式计算速度函数

计算速度的函数通常采用多项式表达，多项式采用常规的表达形式会产生很大的计算误差，不能很好地逼近数据真值，为了减少计算误差，多项式采用逼近性好的切比雪夫多项式组合的方式获得最佳一致逼近多项式计算速度函数［12］。

切比雪夫多项式Tn(x)(n≥0)，定义为：

由公式（15）～公式（17）推得：

切比雪夫多项式组合而成的多项式Qn(x)是连续函数fn(x)的最佳一致逼近多项式的充分必要条件是在区间[a，b]上至少存在n+2 个点x0＜…＜xn+1使得：

其中，i=0，…，n+1，对于所有的i同时α=1（或者α=-1）。

点x0，x1，…，xn+1常常称 为切比 雪夫交替点。

将速度函数f(x)按照切比雪夫正交函数系展开成级数：

低次项速度组合函数如式（22）所示：

式（22）能确定较好逼近。dj很难显式计算，却比较容易进行泰勒展开：

设定速度函数多项式Pn(x)使得公式（24）的误差足够小：

按照切比雪夫多项式展开Pn(x)：

引入记号Qm(x)：

其中m≤n。

所有多项式Qm(x)都是Qm+1(x)的m阶最佳一致逼近多项式，因此：

速度误差估计为：

为了减少运算量，设：

取y=2x，vn-1=yvn+Dn-1，按照递推公式vk=yvk+1-vk+2+Dk获得Pn(x)：

本文采用了简单改进切比雪夫公式，采样4帧速度值分别为d0，d1，d2及d3，计算第5 帧速度值v，为了计算简便，x取值-1。

3.2 有限差分的方法识别速度的野值

设函数表中的节点xi等间距分布：xi=x0+ih，fi为相应的函数值，h称为步长。差fi+1-fi称为一阶差分，用Δfi表示。m阶差分函数值表示：

当x≡x0+ih时，等式（39）成立：

当xi≤ζ≤xi+m时，

可以得到推论：n次多项式的n次有限差分等于常数，而更高阶差分等于零。

根据公式（35），对于m阶差分，误差以系数(-1)j放大。如果函数足够光滑，那么其不很高阶的差分可能很小。通过比较差分结果，可以识别包含误差的函数值，并对其进行修正。

如果某个值fi包含相对较大的误差ε，则在三阶差分中它一定以ε，-3ε，3ε，-ε的形式出现。

根据上述分析，因为速度函数是三次多项式，通过求解三阶差分的值，判断含有误差的测量值，剔除。三阶有限差分去除野值流程图如图3 所示。

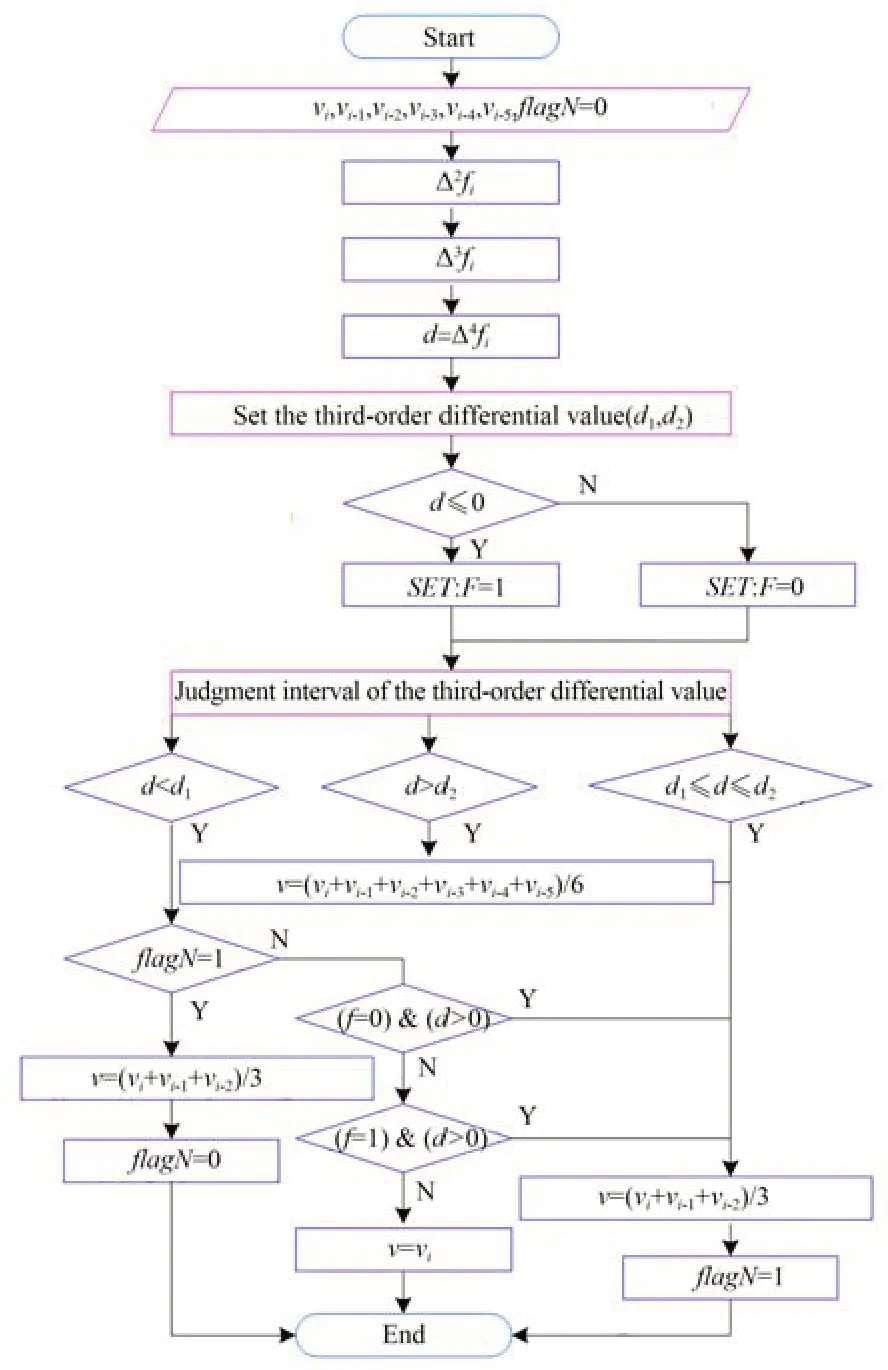
图3 三阶有限差分去除野值流程图Fig.3 Flow chart of third-order finite difference outlier removal

3.3 迭代求解

在通过有限差分的方法识别速度的野值后，对剔除野值的测量值重新进行最佳一致逼近多项式拟合计算，获得的值再进行有限三阶差分剔除，反复迭代，直到误差小于设定的阈值，在速度为40 m/s 时，根据经验速度的误差的阈值选为0.02 m/s。

3.4 测速工作流程图

测速工作步骤：

（1）输入经纬仪数据A，E；

（2）输入激光测距值R，剔野值、滤波；

（3）单站计算目标位置；

（4）位置剔野值、滤波、拟合、外推；

（5）根据速度模型计算速度；

（6）剔野值、滤波保存速度数据。

速度计算流程图如图4 所示。

图4 速度计算流程图Fig.4 Speed calculation flowchart

3.5 实验结果比对

激光测距光电经纬仪在外场进行无人机跟飞实验，设定200 s 飞行时间，飞行最远距离4 000 m，记录从4 000 m 返航图像，匀速飞行速度控制在40 m/s。无人机上装有测速GPS，可以进行速度比对。

3.5.1 激光测得距离滤波实验

设备的激光测距机的距离误差指标为均方差小于1 m，由于激光测距机在测距过程中受到跟踪不稳、噪声、天气和环境等因素影响，测得的距离值具有跳动值，如图5 所示，激光测距获得的距离值与真值对比，最大误差为3.449 m。

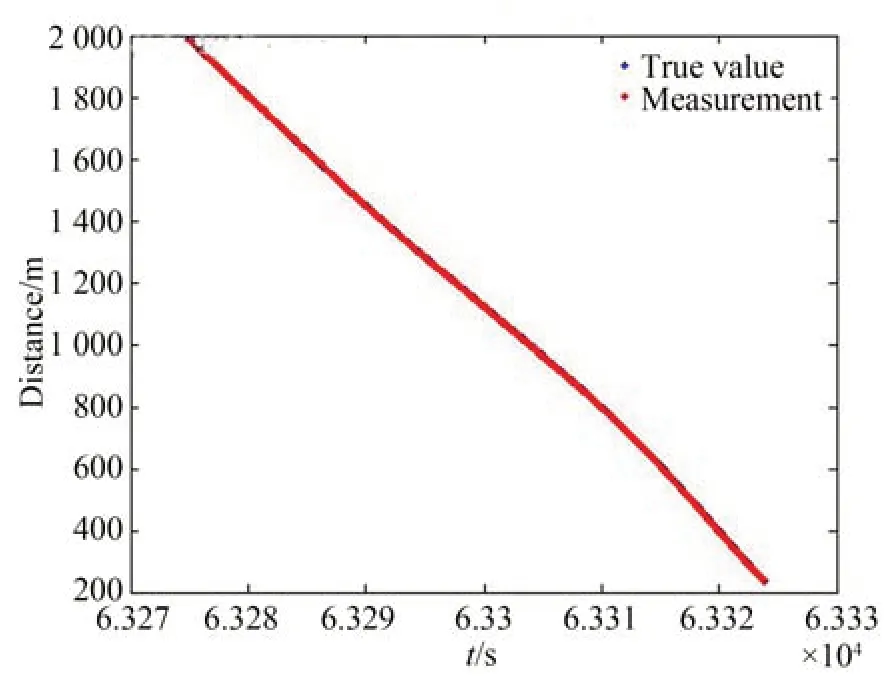
图5 距离测量值与真值对比Fig.5 Comparison of distance measurement values with true values

在实验过程中，必须对距离值进行滤波。通过最小二乘滤波，明显增强测距的稳定性。取目标匀速运行段500 帧数据进行距离滤波前后对比实验。对距离滤波前后的值进行一次差数据计算，在无人机以40 m/s 匀速运行时，采样间隔50 ms，一次差理想值为2 m，如图6 所示距离滤波前一次差幅值范围-1.4～-2.8 m，滤波后的距离一次差幅值范围-1.7～-2.4 m。500 帧数据距离滤波前一次差幅值的标准偏差0.22，滤波后的距离一次差幅值的标准偏差0.13。

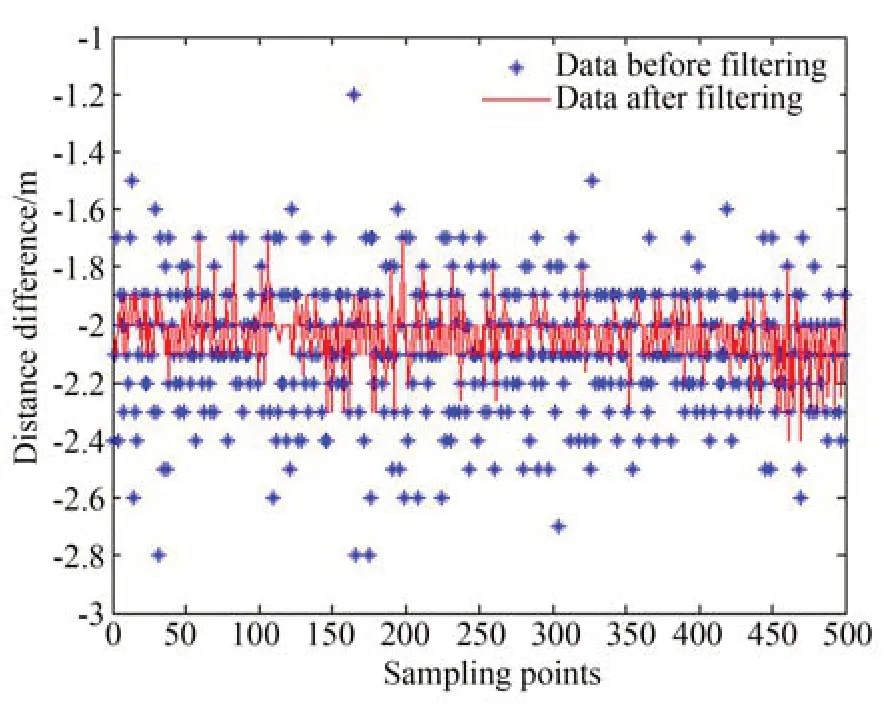
图6 距离滤波前后值一次差数据比较Fig.6 Comparison of first difference data before and after distance filtering

3.5.2 有限差分速度剔野值实验

常规野值剔除方法是处理序列数据的残差，对数据残差进行统计，判断序列数据的野值。有限差分剔除野值的方法，数据差分计算判断野值。根据上述分析，已知速度函数是三次多项式，通过求解三阶差分的值，判断含有误差的测量值，剔除野值。

如图7 所示无人机速度保持40 m/s 匀速飞行，采样频率20 Hz。运行时间100 s。第一组实验数据含有两组小毛刺及两组大毛刺，第二组实验数据含有三组大毛刺，实验结果显示，大野值完全剔除；去毛刺后的图线在采样点200～400 之间、1 000～1 200 之间，相对于去毛刺前的曲线有明显毛刺凸起，经数据分析是三阶差分的低限值取得过低，人为引入扰动。

图7 速度去除野值实验Fig.7 Speed removal outlier test

3.5.3 速度滤波前后与GPS 速度值比对实验

速度滤波实验采用1 000 帧数据，包括起始过度段，无人机速度保持40 m/s 匀速飞行，采样频率20 Hz。运行时间50 s。实时数据取五组数据带入最佳一致逼近多项式拟合计算，获得的值进行有限三阶差分剔除后，反迭代，直到误差小于设定的阈值，在速度为40 m/s 时，根据经验速度的误差的阈值选为0.02 m/s。在测速实验中，可根据不同的实时速度，动态调整误差设定的阈值。速度滤波前后与GPS 差值全部数据对比曲线图如图8 所示。

图8 速度滤波前后与GPS 速度全部数据对比曲线图Fig.8 Comparison curve of all data before and after speed filtering with GPS true values

从图8（b）所示曲线可以看出，滤波后与GPS比对误差最大误差小于0.8 m/s，满足指标1 m/s要求。

3.5.4 几种速度求解方法对比GPS 速度值实验

几种求解速度方法对比GPS 速度值实验如图9 所示。

图9 速度求解方法对比GPS 实验Fig.9 Comparison of Speed Solving Methods with GPS Experiments

如图9 所示，两组数据都是2 000 帧，无人机速度在33～47 m/s 之间变速飞行，采样频率20 Hz。运行时间100 s。全部过程数据曲线显示高斯（Gaussian velocity Solving,GS）有大的毛刺存在；截取尾部数据扩大曲线显示卡尔曼（Kalman filtering speed solution,KLM）数据有较大滞后。最佳一致逼近多项式（Optimal Uniform Approximation,OUA）获得速度与GPS 速度值比对，时许滞后一帧，50 ms，误差小于0.8 m/s。

4 结论

本文根据激光测距经纬仪的高精度、实时性的测速要求，提出了最佳一致逼近多项式的测速方法，本方法在实际使用中，主要采用切比雪夫三阶多项式来逼近速度真值，利用三阶有限差分法剔除速度野值，根据实时速度，动态调整速度迭代误差阈值，使速度精度更高。本方法获得速度与GPS 速度值比对，实时性好，延时50 ms；速度精度均方差为0.8 m/s，满足设备的指标要求。本文采用的有限差分法，也可以应用在变化缓慢场景图像去高阶噪声。