基于微观市场结构的股票日内价格趋势预测研究
杨龙光
[提要]本文基于演化博弈模型,通过分析在t时刻股票投资者的动态行为,得到投资者总的期望收益,并通过构建动态复制方程得到投资者行为的解。本文进一步通过市场深度来刻画投资者行为与股价的关系,并通过对资金实力和相关参数等取值的讨论,得到了基于微观市场结构的股票日内价格预测模型。本文随机抽取了多日和单日的100只不同股票的分钟数据进行实证分析,并通过与另外四种方法进行比较,证明了本文方法的准确性和有效性。本文的研究不仅为投资者的投资决策提供了很好的参考,对其他金融资产的日内价格预测研究也具有借鉴意义。
引言
2021年8、9月,我国A股市场连续40多个交易日成交量突破万亿,业内普遍认为,量化交易在其中贡献了相当大的成交量。量化交易最早出现在20世纪70年代的美国,日内高频交易是其最显著的特征;我国股市长期实施的是T+1制度,不具备高频交易的基础。2010年,我国正式推出了融券业务,使得以投资组合的方式达到T+0的交易效果成为可能;2017年,AlphaGo与柯洁的围棋之战带火了深度学习概念,再次给国内的量化交易发展注入了一剂强心针。
量化交易以先进的数据模型代替人为的主观判断,最大程度降低投资者情绪带来的影响,避免做出不理性决策。由于信息不对称的存在,投资者(尤其是散户)无法及时、全面地获得关于股价的全部信息,甚至可能盲目相信虚假信息,因此投资者很可能在买卖过程中做出错误决策,造成股价波动。在信息化发展的新阶段,社交媒体盛行,信息传播速度非常之快,加之“羊群行为”的推波助澜,更多投资者可能会放弃自己的私有信息,依照公共信息来决策,使得股价更加偏离其真实价值。这使股价不能反映市场上的全部信息,降低信息透明度,严重时使资源不能得到有效配置,扰乱资本市场秩序。因此量化交易这种客观的投资方式对投资者的投资决策和资本市场的稳定具有积极作用,这也是本文构建基于微观市场结构的股票日内价格预测的意义所在。
已有文献也有考察买单和卖单对市场价格的影响,但大多只是得到两者之间的相关关系,并未具体探讨买卖单影响市场价格的具体机制。基于此,本文从投资者行为的角度出发,结合市场深度,构建起股票日内价格预测的理论模型。
本文余下部分组织如下:第二部分是文献综述;第三部分是本文模型的构建过程,详细讨论了股票买卖双方在决策时面临的多种可能,以得到更准确的结果;第四部分是实证分析,分别以单日和多日结果展示验证了本文方法的准确性;第五部分是结论。
一、文献综述
(一)高频价格数据
李志辉等(2021)采用分钟数据构造了A股市场操纵指标,并考察了机构投资者在市场操纵中所扮演的角色。[1]李志辉等(2020)利用日内高频价格数据,构造了内幕交易的代理变量,并考察了内幕交易对价格效率的影响;[2]尹海员等(2019)从上证指数股吧的实时发帖中进行文本挖掘,构造了日内高频情绪指标,并探讨了其对日内收益率的预测作用;[3]此外,还有一些学者也对高频价格序列进行了统计或套利方法上的研究(罗乐,2021;[4]王良等,2018;[5]王江涛等,2021[6])。
(二)买卖价差与流动性
屈文洲等(2002)利用限价单的买卖报价,构造了深圳股票市场的买卖价差指标,并考察了波动率、价格和成交量等,对买卖价差的影响。[7]陈海强等(2020)利用买卖价差构建了6个单项指标,然后通过主成分分析降维后,构造了流动性因子,验证了流动性因子与股票收益率之间的正向关系。[8]
(三)买卖报价单
屈文洲等(2011)通过主动性买卖单笔数和消息出现概率等因素,构建了信息不对称指标,并考察了该指标对企业新增投资的影响。[9]马丹等(2020)以主动性买卖单为基础,计算了订单流不平衡指标,并通过该指标对高频价格序列收益率的预测程度,构建了市场价格效率指标。[10]文章进一步考察了流动性供给水平对市场价格效率的影响;朱菲菲等(2019)利用买卖双方驱动单数量,构建了羊群行为程度的衡量指标,并考察了羊群效应的影响因素,以及与价格效应之间的关系。[11][12]
现有的微观市场结构文献大多关注高频价格和买卖单两个方面,前者衍生出对市场操纵、内幕交易的识别,以及价格序列预测等研究,后者则多将买卖单与流动性、价格效率或羊群效应挂钩。买卖单会影响日内价格变动,这是联系两方面研究的内在逻辑,但是,现有文献在买卖单对市场价格的具体影响形式上探讨得并不充分,大多采用比较简单的比值法,优点是能直接体现变量间的大致单调关系,缺点是忽略掉了背后可能存在的复杂规律。
因此,本文试图从投资者行为出发,结合市场深度,构建一个基于微观市场结构的日内价格预测模型。
二、模型构建
本文理论模型的逻辑是:可以将市场上所有的投资者分为买方和卖方两类,在某一时刻t,买卖双方会依据各自对未来价格的判断,决定买入、卖出的数量;双方的投资决策共同决定了t+1时刻的股价。也就是说,t时刻的信息,通过影响t时刻买卖双方的投资行为,影响了t+1时刻的股价。如果能通过模型,对信息影响行为的机制进行适当刻画,那么理论上,当前时刻的信息应该对t+1时刻的股价有一定的预测能力。
(一)买卖双方行为的刻画
根据以上分析,本文选择演化博弈模型来刻画买卖双方的动态行为。
其中,Pt是当前t时刻的股价。买方的行为包括买进(概率pbd)和观望(概率1-pbd),卖方的行为包括卖出(概率psd)和观望(概率1-psd)。对于买方而言,他会对未来价格有两个预测,一是当卖方实施卖出行为时,买方预测未来价格为Eb1Pt+1;对应于实际中,是空方力量较强,或者股价上涨阻力较大的时候。二是当卖方观望时,买方预测未来价格为Eb2Pt+1;这对应于实际中的空方力量较弱,或者股价上涨阻力较小的时候。对于卖方而言,在一个以做多为主的市场中,同时不考虑机会成本的时候,其收益主要体现在持股观望状态,此时卖方对未来股价的预期为EsPt+1。
收益方面,当买方决定买进时,他对自己的收益预期为Eb1Pt+1-Pt或者Eb2Pt+1-Pt,分别对应于卖方力量较强和较弱两种情况;当买方观望时,收益当然为0。当卖方决定卖出时,他的收益为0,意味着未来股价无论涨跌,都跟他无关;当卖方决定观望时,意味着他认为未来股价还会上涨,他对自己的收益预期为EsPt+1-Pt。需要特别说明的是,本文假定当买卖双方都观望时,股价不会发生变化,即股价完全是由买卖双方的行为内生决定的。
在演化博弈的框架下,本文将买卖双方的行为概率视作动态变量,同时基于表1,买方观望行为的期望收益为f2=0;买方买进行为的期望收益为:
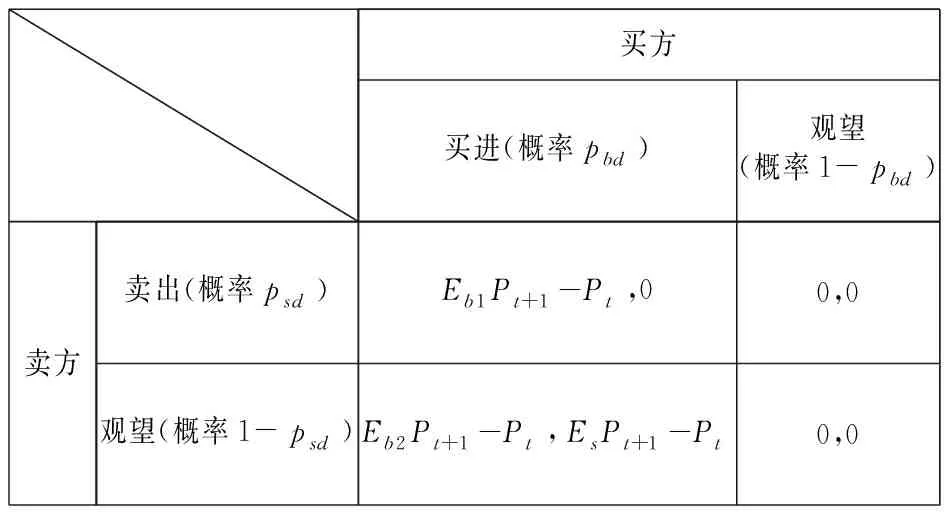
表1 买卖双方博弈收益矩阵

表2 所有变量说明
f1=psd[t]*(Eb1Pt+1-Pt)+
(1-psd[t])*(Eb2Pt+1-Pt)
(1)
因此,买方总的期望收益为:
f0=pbd[t]*f1+(1-pbd[t])*f2
=[psd[t]*(Eb1Pt+1-Pt)+
(1-psd[t])*(Eb2Pt+1-Pt)]*
pbd[t]+0*(1-pbd[t])
(2)
其中,pbd[t]和psd[t]分别代表买进和卖出概率是随时间变化的变量。
卖方卖出行为的期望收益为g1=0;卖方观望行为的期望收益为:
g2=pbd[t]*(EsPt+1-Pt)+
(1-pbd[t])*0
(3)
因此,卖方总的期望收益为:
g0=pbd[t]*g1+(1-pbd[t])*
g2=(1-psd[t])*pbd[t]*(EsPt+1-Pt)
(4)
用动态复制方程构建买卖双方的行为(杨龙光和王鹏,2019):
p'bd[t]=pbd[t]*(f1-f0)
(5)
p'sd[t]=psd[t]*(g1-g0)
(6)
通过求解微分方程(5)、(6),①同时假定买卖双方的行为只有0和1两期,即当期信息只用于指导下一期决策,而不涉及未来多期决策,那么买卖双方的行为实际上就变成了“一次性决策”,从而可以得到不含时间趋势变量t的买卖双方行为的解:
pbd=
(7)
(8)
公式(7)表明了,买方的行为受到自己对未来股价的预期,以及卖方卖出行为的影响;公式(8)表明卖方行为受到自己对未来股价的预期,以及买方买进行为的影响。
(二)投资行为影响股价
买卖双方的行为,会体现为各自在当前价位Pt的成交量,通过限价单或市价单的方式,推动股价向成交量占优一方变动至Pt+1。因此,成交量与股价在微观层面存在完全的因果关系,本文通过市场深度来刻画这种因果关系:
(9)
在式(9)中,VB和VS分别是买卖双方的成交量;ka≥0和kb≥0分别是下跌和上涨时的市场深度,衡量的是一单位成交量会造成多少价格变动。若VB≥VS,即买方成交量大于卖方成交量时,则:
ΔP=kb*(VB-VS)
(10)
若VB ΔP=ka*(VB-VS) (11) 进一步地,买卖双方的成交量VB和VS可以看作是由买卖概率决定的: VB=pbd*V_buy (12) VS=psd*V_sell (13) 其中,V_buy和V_sell是买卖双方各自的全部资金量,即资金实力。一个合理的假设是,买卖双方的资金实力相等且不随时间变化,即买卖双方的总体实力均衡,是一个相对固定的常数,不存在买方的资金实力系统性大于或小于卖方的情况,也不存在双方的资金实力随时间不断变化的情况。令双方的资金实力为V,则市场资金的流入流出,就是由买方买进和卖方卖出的概率决定的: VB=pbd*V (14) VS=psd*V (15) 我们将公式(7)、(8)、(12)、(13)代入公式(9),可以得到市场参与者对下一期的股价预期: (16) 公式(16)描述了股票市场上买卖双方的各自行为对下一期股价的影响机制。考虑到实证部分的数据可获得性,我们进一步地做了如下假设: (1)令资金实力V=1,这相当于忽略掉V的绝对大小,会造成公式(16)中ΔP的估计出现偏差,从而使得估计得到的E(Pt+1)的数值失去了参考意义。不过,从公式(10)、(11)、(14)、(15)可推知,ΔP和V是线性的正相关关系,从而令常数V=1,只会改变ΔP的变化大小,而不会改变其变化方向,从而仍然可以获得下一期股价E(Pt+1)波动方向的信息。 (2)令Eb1Pt+1=Pt+0.05,Eb2Pt+1=EsPt+1=Pt+0.1。根据表1,只有当买方决定买进时,股票价格才会变动。而同时,如果卖方决定观望,则市场多头占绝对优势,股票价格涨幅较大;如果卖方决定卖出,则市场多头占相对优势,股票价格涨幅较小。进一步地,假设买方买进,且卖方观望时,买卖双方对未来股价的预期相同,于是有:Eb2Pt+1=EsPt+1=Pt+ΔP1>Eb1Pt+1=Pt+ΔP2。由于上一步假设V=1,已经造成未来股价的预测误差,从而将重点放在预测波动方向上,因此在相同的思想下,可以假设ΔP1=0.1,ΔP2=0.05。 通过以上两步假设,公式(16)变为: (17) 本文的数据来源为万得数据,时间为2021年四季度,②单次结果基于在该时间段内任意抽取的某一交易日;只关注连续竞价时段,周期为分钟数据。股票样本为在所有A股中随机抽取的100只股票。 公式(17)中一共有5个变量,分别是:当前的市场价格Pt、下跌时的市场深度ka、上涨时的市场深度kb、买方的买进概率pbd、卖方的卖出概率psd。 对于市场深度,本文的计算方法为:当t期的价格变动ΔPt<0时,计算t期的价格变动与当期成交量之比ΔPt/|Vt|,作为下跌市场深度ka;此时kb取上一期的值,初始值为0。③当t期的价格变动ΔPt≥0时,计算t期的价格变动与当期成交量之比ΔPt/|Vt|,作为上涨市场深度kb;此时ka取上一期的值,初始值为0。 依据前文所述,单次的实证数据经过了交易日和股票两次抽样,即在2021年四季度中随机抽取1个交易日之后,进一步在全部A股中随机抽取100只股票;并且每次抽取交易日之后,都要对股票进行抽样,这样,即使网站限制了可获取历史交易日的最大天数,被抽取的股票也很难重复,从而可以达到较好的随机性。表3展示了随机抽取的2021年11月30日的100只股票描述性统计。④ 表3 2021年11月30日抽样结果的描述性统计 从表3可见,本次抽样抽取了股价为2.69元~183.696元的100只股票;下跌和上涨的市场深度都是在0~1范围内,均值分别为0.0461和0.0544,代表每1元的卖出或买入成交量,平均会带来0.0461元和0.0544元的价格下跌或上涨;买卖概率均值和中位数都为0.5左右,只有卖出概率的均值为0.4881,代表该交易日内,卖方卖出的意愿相对较弱。 本文的评价采用两个思路,一是准确率,二是绝对偏差。 准确率考察的是预测股价的变动方向,是否与实际股价的变动方向一致,采用计算公式: (18) 其中,accuracyi是第i只股票的准确率,Pi,t是第i只股票在t时刻的价格,E(Pi,t)是估计得到的第i只股票在t时刻的预测股价,T是该股票交易日内连续竞价阶段的交易分钟数,1(·)是示性函数,若括号中条件满足,则函数值为1。如果预测方法是无效的,那么预测得到的股价序列与真实的股价序列之间是不相关的,那么理论上,二者符号相同的概率应为50%,另外50%是预测下跌但实际上涨,以及预测上涨但实际下跌两种情况。进一步地,依据本文模型以及比较方法的设计思路,预测股价序列与真实股价序列之间应是正相关关系,此时公式(18)的计算结果应该大于0.5,偏离得越多,代表预测股价序列的有效预测越多,而不仅是靠“猜”。 本文同时也给出了绝对偏差的结果,⑤采用计算公式: errori=Pi,t-E(Pi,t) (19) 其中,errori是第i只股票预测股价相对于真实股价的误差序列,Pi,t是t时刻、第i只股票的真实价格,E(Pi,t)是预测模型对t时刻、第i只股票股价的预测。由于每只股票在交易日内有近240分钟的连续竞价时段,为了对每一只股票给出一个唯一的结果,本文进一步统计了每只股票errori序列的均值和中位数,这样每次抽样,都会形成100只股票的误差均值和误差中位数序列。 1.比较方法 本文的预测思路,实际上是通过第t-1期的市场信息预测第t期的价格,在已有文献中,这种逻辑一般被用来衡量市场价格效率,即:若t期和t-1期的价格具有较强的相关性,那么市场是无效率的(李志辉和孙广宇,2020)。因而本文选择如下思路构造两类共四个比较方法:一是股价滞后一期的lag_1方法,将t-1期价格直接视作对第t期的价格预测;二是AR(1)方法,即利用时间序列AR(1)模型,得到对第t期价格的样本外预测,并进一步划分为10分钟、20分钟和30分钟三个不同参数的AR(1)方法。 2.单次抽样结果展示 下面是与表3相同的2021年11月30日抽样,经过本文模型与比较方法分别进行股价预测后,关于准确率和误差的进一步结果展示。 图1从上到下、从左至右,分别是本文方法与滞后1期lag_1方法、AR(1)10分钟历史方法、AR(1)20分钟历史方法、AR(1)30分钟历史方法的比较结果,其中实心直方图为本文方法的结果,空心直方图为比较方法的结果,垂直线为x轴上的50%标记线,当直方图在标记线右侧集聚时,代表该方法是有效的。左上图显示了对于100只抽样股票中的绝大部分,本文方法的准确率都是超过了50%的,最大能到65%左右,通过计算,中位数为52.99%。lag_1方法看上去似乎并无差别,但中位数为52.38%,略差于本文方法。其余三图展示了类似的结果:相对于本文方法,三种参数的AR(1)比较方法的准确率都围绕在0.5标记线附近,或者略处于其左侧,代表其预测是“涨跌参半”的,不存在有效性。 图1 本文方法与四个比较方法的准确率直方图统计 图2是100只股票日内误差均值的直方图统计,若绝对值越小,则代表估计的股票价格与真实股价的日内误差越小,竖线标注了误差为0的位置。左上图显示了本文方法的误差围绕在0附近,略微右偏,根据公式(19),代表本文模型可能会系统性地低估股价。lag_1方法与本文模型的差异不大,但是也存在低估问题。其余三图的误差范围较大,虽然AR(1)模型采用OLS估计,但显然其样本外预测的效果并不好,而就本次抽样结果来看,AR(1)模型结果存在左偏现象,即存在系统性高估股价的问题。 图2 本文方法与四个比较方法的误差均值直方图统计 图3是100只股票日内误差中位数的直方图统计,同样是绝对值越小越好。图3显示了与图二类似的结果,只不过对所有方法而言,左偏或右偏的现象变得不太明显。 图3 本文方法与四个比较方法的误差中位数直方图统计 3.多次抽样结果展示 为了避免单次抽样结果存在的偶然性,本文进一步重复了30次抽样,以更全面地考察本文方法的效果。为了对多次重复抽样的结果进行展示,本文对单次抽样结果进一步做了如下处理: (1)统计单次抽样中,100只股票准确率的中位数,如前文所述,该值应该大于50%,才有可能大部分股票的准确率超过50%; (2)统计在单次抽样的100只股票中,本文方法准确率优于比较方法准确率的概率,作为相对准确率。如果本文方法优于比较方法,那么相对准确率应该大于50%,代表本文方法在过半的股票上,估计准确率是更好的; (3)统计在单次抽样的100只股票中,本文方法误差均值的绝对值小于比较方法的概率,若该值大于50%,代表本文方法在大部分股票上的估计误差更小; (4)统计在单次抽样的100只股票中,本文方法误差中位数的绝对值小于比较方法的概率,大于50%代表本文方法的估计误差更小。 图4的横坐标为30次抽样,纵坐标是每次抽样的100只股票的准确率中位数。依据前文分析,准确率大于50%才能说明方法有效,从图4可见,本文方法的准确率中位数大致在53%左右,意味着如果对多只股票的涨跌方向进行预测,那么其中有一半股票的准确预测率能超过53%。比较方法中表现最好的是lag_1方法,但中位数仍略低于本文方法;其他三个基于AR(1)的方法表现较为接近,且准确率低于50%,意味着样本外的预测反而体现出了“反转效应”,即模型预测为涨,而实际却是下跌。但是这种“反转效应”并不明显偏离于50%,所以难以作为反向指标。 图4 各方法的准确率中位数(30次抽样) 图5的横坐标是30次抽样,纵坐标是单次抽样的100只股票中,本文方法的准确率高于其余各个比较方法准确率的概率。如果概率值大于50%,代表在单次抽样中有超过一半的股票,本文方法是优于比较方法的。具体来看,本文方法的准确率在近60%的股票上,是优于lag_1方法的,而相对于AR(1)的三个方法,本文方法在约65%的股票上有着更好的准确率。 图5 本文方法相较于比较方法的优势(准确率) 图6的横坐标是30次抽样,纵坐标是单次抽样的100只股票中,本文方法的误差均值低于各个比较方法误差均值的概率。如果概率值大于50%,代表在一多半的股票上,本文方法相对于比较方法的误差更小。具体来看,本文方法只在约40%的股票上,有着小于lag_1方法的误差均值,这与前文的分析基本一致,即本文方法重在对走势方向的估计,而非精确价格的估计。而相对于AR(1)的三个方法,本文方法的低误差优势体现在了约90%的股票上,说明AR(1)模型的样本外预测效果并不理想。 图6 本文方法相较于比较方法的优势(误差均值) 图7的横坐标是30次抽样,纵坐标是单次抽样的100只股票中,本文方法的误差中位数低于各个比较方法误差中位数的概率。从图中结果来看,本文方法只有约15%的股票,误差中位数能低于lag_1方法,远低于图6对均值的考察结果。这是因为对单次抽样的100只股票中的大部分而言,本文方法的日内估计误差存在左偏,而根据公式(19),这可能是因为本文方法系统性地高估了t+1期的股价所致。对于AR(1)的三个方法,本文方法的误差中位数优势也有下降,相较于图6的均值优势,图7的中位数优势下降到了80%左右。 图7 本文方法相较于比较方法的优势(误差中位数) 本文构建了一个基于微观市场结构的股票日内价格预测模型,并使用A股市场上的高频数据对该模型进行实证检验。 在文章的前半部分,构建了股票买卖双方的演化博弈矩阵,并通过求解动态复制方程,得到买卖双方投资行为的方程表达式;由于本文认为t时刻的信息会通过影响买卖双方t时刻的投资行为进而影响t+1时刻的股价,因此本文通过市场深度来刻画投资行为与股价的因果关系,并通过进一步对投资者资金实力与相关参数的讨论,得到投资者行为对下一期股价的影响机制。 在文章的后半部分实证分析中,首先为前半部分得到模型中的变量赋予具体的计算方法,之后随机抽取2021年四季度A股市场的交易数据对本文模型进行实证检验。结果发现,本文模型能较好地刻画投资者行为与股价之间的关系。就单次抽样结果而言,对于抽取的100只股票中的绝大部分,本文方法预测的准确率都大于50%,并且估计的误差均值和误差中位数都集中在0附近,初步验证了本文方法的可靠性。多次抽样结果显示,如果对多只股票价格进行预测,本文方法对一半以上的股价预测的准确率超过53%,并且在60%左右的概率下超过其他三种方法,进一步说明本文方法对股价的走势预测是可以借鉴的。 总体而言,本文提出了一个基于投资者行为的股价预测模型,并使用市场交易数据对该模型预测的股价走势进行了验证,具有较强的理论意义和现实意义。在未来的研究中,学者们可以将本文的方法应用到其他金融资产(例如期权、期货)或者数字货币上。此外,本文的方法虽然只预测股价走势,不精准预测股票价格,但对投资者也有一定借鉴意义。 注释: ①通过软件Mathmatica 11.1计算得到。 ②由于万得最多只能获取近一个月内的高频数据,因此本文的实证数据来源于成文时的时间段。 ③由于股价收益率几乎都是零均值期望,因此ka和kb更新很快,初始值的影响不大。 ④由于以下原因,每次抽样可能存在部分缺失值:当日停牌、某时刻无成交量使得市场深度计算出现0/0型错误、买卖挂单无变化使得R_bidj,t计算出现0/0型错误。 ⑤虽然依据公式(17),本文的重点并非在于对股价的精准预测,而是估计股价变动的方向,不过为了进行完整的比较,我们还是展示了股价预测误差的结果。而为了使本文的预测股价,与后文所选比较方法的预测股价进行更为合理的比较,本文在预测股价时,首先对原始股价进行了归一化处理。
三、实证分析
(一)描述性统计

(二)结果评价方法
(三)比较方法与评价






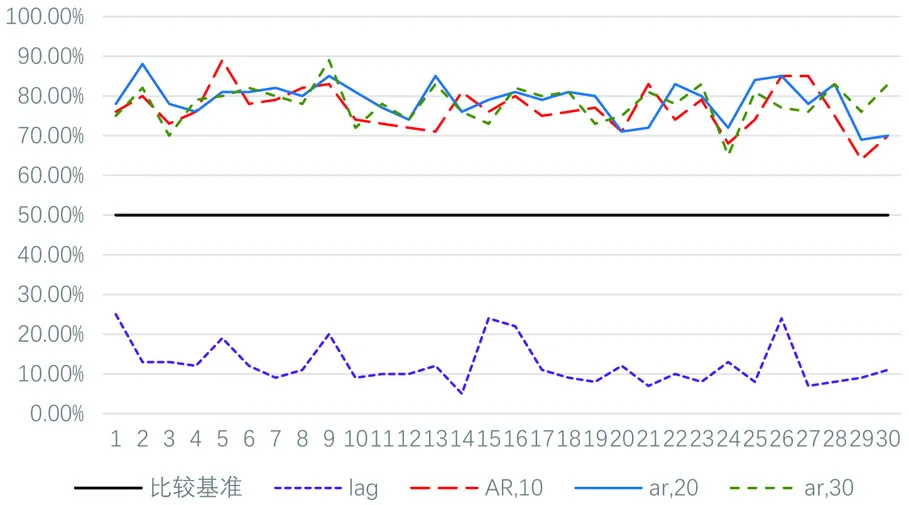
结论

