锯齿尾缘风力机叶片气动及噪声性能研究
马俊祥,赵振宙,郑康乐,张克凡,吴昊,张爽
(1.华能国际电力股份有限公司河南清洁能源分公司,郑州 450003;2.河海大学能源与电气学院,南京 211100;3.华能临河热电厂,内蒙古 巴彦淖尔 015002)
风力发电产业日益成熟,风电机组不断向着大型化、规模化发展[1-2],风力机叶片的噪声声压级也随着叶片的增长而不断增强。水平轴风力机叶片引起的环境噪声污染,在重视绿色低碳、可持续发展的当下是风电推广发展的重大阻力,因此控制运行噪声是风力机设计过程中需考虑的重要因素之一[3]。风力机运转产生的机械噪声与气动噪声是风电场噪声的重要来源,其中机械噪声通过改进机械部件工艺已经得到了很好的抑制[4]。而气动噪声则通过依据仿生学原理改造的锯齿型风力机叶片进行控制。根据最新的研究显示,风力机叶片的锯齿结构能够改变传统叶片模型边界层的流动方式,使流动分离得到改善[5]。
GHASEMIAN[6]基于五种不同的叶尖度比,运用不可压大涡模拟(LES)模型和FW-H声学来模型研究垂直轴风力机气动噪声,研究表明辐射噪声强度和转速具有直接关系,OASPL(总声压级)随接收器的距离呈对数趋势变化。GRUBER[7-8]在不同流速和攻角工况下对三十七个锯齿尾缘翼型进行实验测试,结果显示叶片前缘的锯齿结构能降低噪声,叶片后缘的锯齿结构能减少尾流。CHEN[9]等人基于k-ωSST湍流模型和FW-H 方程在不同风速(3~25 m/s)、不同转速(36~120 r/min)下对NREL Phase VI翼型进行气动噪声模拟,计算发现,在相同工况下风速越大,气动噪声越大,风轮转速越大,气动噪声越大。张兆德[10-11]等采用LES/Lighthill方法对二维翼型及1.5 MW大型风力机进行研究,发现相对风速对噪声的影响比攻角更大,进而提出降低风力机气动噪声的措施。黄乾[12]运用嵌入式大涡模拟和FW-H方程分析了锯齿对NACA 0018翼型的非稳态特征,研究表明长锯齿翼型影响了边界层的运动,降低了噪声的总声压级,具有降噪功能。OERLEMANS[13-14]团队应用相控阵麦克风阵列检测技术系统地研究了大型风力机的噪声声源,测试结果表明宽带后缘噪声是风力机的主要声源。
结合前人仿生锯齿的研究成果,本文以NREL Phase VI风力机作为基本模型,运用数值模拟的方法,研究在7 m/s风速工况下锯齿尾缘结构对NREL Phase VI风力机的气动及噪声特性的影响,进一步认识降噪机理,为找出理想的锯齿结构并应用于风力机降噪提供参考。
1 数值模拟方法
1.1 声学控制方程
1.1.1 Lighthill方程
Lighthill在1952年推导出了Lighthill方程,是认识和研究气动声学的基础方程。
(1)

1.1.2 FW-H方程
根据已知的Lighthill基本方程整理可得:
(2)
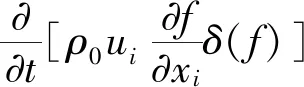
对风力机的气动噪声来说,单极子声源主要是叶片厚度噪声,偶极子声源主要是因为叶片非定常气动力。在低速流动中,偶极子是气动噪声的重要来源,四极子声源可以忽略。当达到超音速时,四极子源在气动噪声中显得非常重要。
1.2 湍流模拟
采用分离涡模拟(DES)的方法来控制流动。DES是Spalart在1997年提出的结合大涡模拟(LES)与雷诺平均(RANS)的混合模拟方法:在近壁面区运用RANS方法进行模拟,大量减少壁面的网格数量;在远壁面的主要流场区域运用LES方法进行模拟,保留了在主要流场区域运用大涡模拟得到的流场细节。DES 97是基于S-A模型,是DES最早的形式,其表达式为:
(3)
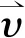
(4)
(5)
(6)
(7)
(8)
(9)
式(7)中S为涡量的绝对值,此外
(10)
g=r+cw2(r6-r)
(11)
(12)
常数项取值为:
κ=0.41,σ=2/3,cb1=0.135 5,cb2=0.622

(13)
式中:Δ=max(Δx,Δy,Δz),Δ取流场中x,y,z三个方向网格的最大值;参数CDES=0.65;dw表示网格中心到壁面的距离。这样,在dw
2 锯齿型风力机叶片气动数值模拟
2.1 几何模型
以NREL Phase VI风力机叶片为基本模型[15],对其叶片尾缘进行切割改型,得到锯齿尾缘NREL Phase VI风力机叶片。风力机是全部由S809翼型组成的两叶片水平轴风力机,翼型相对厚度0.209 5,风力机叶轮直径10.058 m,叶尖桨距角3°,用MATLAB程序进行坐标变换,输出.ibl文件并导入到Proe程序中进行叶片建模。NREL Phase VI锯齿尾缘叶片是保持原型叶片各个截面翼型弦长大小不变并将翼型尾缘长度约7.5%弦长处改造成锯齿形状而成,如图1所示。

图1 风力机模型
2.2 计算网格
首先对NREL Phase VI风力机原型用ICEM进行非结构性网格划分,然后使用Fluent模拟计算,再对结果进行后处理分析。本文不考虑塔架的影响,计算流场中入口与风力机的距离为6R(R为叶片半径长度),出口与风力机的距离为10R,流场壁面与风力机的距离为6R,使风力机尾流得到充分发展并减少了壁面对风力机的影响,数值模拟结果更为准确。为保证模拟结果的稳定性和准确性,先进行k-ωSST定常计算至结果收敛,再进行2周k-ωSST非定常计算,最后使用DES方法计算一个周期。
2.3 计算结果分析
2.3.1 锯齿对叶片表面压力系数的影响
选取5个具有试验数据的展向位置,进行压力系数的对比,进一步分析锯齿结构对风力机的影响。展向位置分别为0.300R、0.467R、0.630R、0.800R和0.950R。
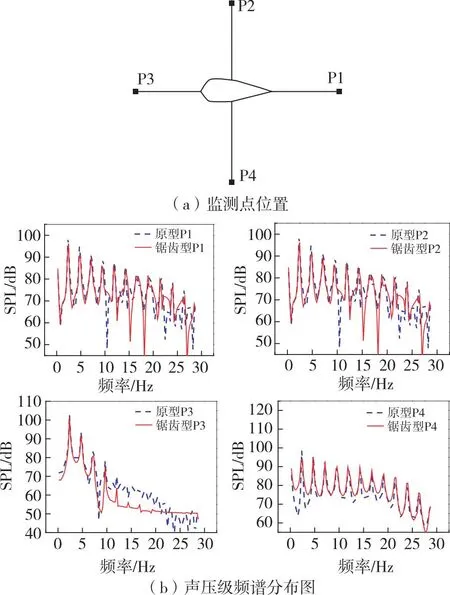
如图2所示,为7 m/s风况下的压力系数曲线图。在展向r=0.300R、x/c<0.3和x/c> 0.5处,风力机原型与试验值的压力系数吻合程度较好;而在x/c=0.4时,吸力面和压力面的压力系数的试验值明显高于数值模拟计算值, 风力机锯齿型与原型的压力系数曲线重合。在展向r=0.467R处,风力机原型的数值模拟值与试验值一致,在x/c>0.85处,由于锯齿尾缘漏气的原因,风力机原型下表面压力系数高于锯齿型压力系数。在展向r=0.630R处,风力机原型的模拟压力系数值与试验值吻合度很高,在靠近压力面前缘点位置处,风力机原型的压力系数值大于锯齿型。在展向r=0.800R处,风力机原型的模拟压力系数值与试验值吻合度最低。特别是在x/c<0.7处,压力面的系数绝对值远大于数值模拟值,是转矩出现差异的主要原因。在r=0.950R叶尖处与0.4 图2 7 m/s风况下叶片表面压力系数图 2.3.2 锯齿对叶片表面流动的影响 如图3所示,为7 m/s风况下NREL Phase VI风力机原型与锯齿型的表面压力云图和极限流线图。 图3 7 m/s风况下叶片表面压力云图和极限流线图 从云图上看,最大的压力区域出现在压力面叶尖部分前缘处,最小压力区域出现在吸力面的前缘处。在展向r>0.4R区域,尾缘段的压力值明显比中间段的大。从极限流线图上看,在叶片的压力面,两者流线相似;在叶片吸力面靠近叶尖尾缘区域,风力机原型相较于锯齿型出现了明显的分离现象,这说明叶片尾缘锯齿结构改变了壁面的分离模式,使流场得到改善。风力机原型的径向流动现象也比锯齿型更为明显,锯齿结构使叶根及连接部分产生了复杂的流动,有效地改变了叶根部分的流动状态。 利用DES方法和FW-H方程,对NREL Phase VI风力机的气动噪声进行数值模拟,本节针对气动噪声的模拟结果分析声信号声压指向性和监测点噪声频谱。选取的时间步长为0.017 4 s,风力机的转速为72 r/min,旋转一周大约需要0.833 4 s。 2.4.1 声信号声压指向性 监测点位置:如图4所示,分别于弦向l1=0.5 m、l2=2 m范围处在展向平面R=5.029 m布置五层,依次为0.300R、0.467R、0.630R、0.800R、0.950R。以叶片翼型的气动中心(0,0,0)为原点,进行两周设置,其中点间隔为15°,第一周为0.5 m,第二周为2 m。设x轴负方向180°,x轴正方向0°,y轴负方向270°,y轴正方向90°。 图4 风力机叶片噪声监测点位置 如图5所示,为7 m/s风速工况下风力机原型与锯齿型的声场指向性分布规律图,纵坐标SPL代表声压级。从图中可以看出,在7m/s风速工况下,同一展向平面和同一弦向范围内,风力机原型和锯齿型的声场指向性分布形状都相似,且除0°和180°方向处的监测点位置外,风力机锯齿型的声压级数值都低于原型,证明了锯齿结构可以有效降低风力机叶片声压级;而0°和180°方向出现的差异是改变其指向分布的体现,尤其是在展向平面r=0.630R和r=0.800R的0°方向监测点处,风力机锯齿型声压级也能得到较好的优化结果。同时在展向平面r=0.300R和r=0.467R的330°方向处,由于出现了尾迹流扰动,使得此处风力机原型声压级略小于锯齿型。 图5 声场指向性分布图 另外由图可知,在同一展向平面,l2=2 m弦向范围的噪声声压级除个别点外,均小于l1=0.5 m处的声压级,这表明与风力机叶片的距离越大,噪声的声压级越小,基本符合翼型声压级分布规律。l2=2 m的曲线很好地显示了偶极子特性;在l1=0.5 m处,由于该展向在截面翼型的实际攻角在α=15°附近,0°和180°方向监测点的声压级明显比l2=2 m处监测点的值小,且最大值出现在15°和165°方向监测点处,这一结果与前缘点噪声声压级最高的规律一致。 在同一弦向范围内,当l1=0.5 m时,风力机原型的大声压级在0°~30°、150°~195°和330°~360°方向之间,极大值集中出现在15°和165°方向处;最小噪声声压级在r=0.300R平面出现,最大噪声声压级在r=0.630R和r=0.800R平面处相互交错出现,其中在0°~15°、150°~165°和330°~360°方向下,r=0.630R平面处监测点的声压级比r=0.800R平面处监测点的声压级大,而在180°~210°方向下,r=0.630R平面处监测点的声压级比r=0.800R平面处监测点的声压级小,其他方向几乎一致。当弦向范围为l2=2 m时,r=0.300R、r=0.467R、r=0.630R和r=0.800R平面都表现出极好的偶极子特性,其中最大连线方向位于0°和180°处,最小连线方向位于90°~270°处。而r=0.950R平面则在90°~270°处连线方向最大,0°和180°处连线方向最小。 2.4.2 声压级分布频谱 风力机的气动噪声是周期性旋转的叶片与流动空气质点作用产生的压力脉动经由空气传播形成的。噪声声压级强度随着气流相对速度的增大而增强。旋转噪声具有离散性,基频时对应的噪声最强,高次谐音逐渐减少。 基本频率一般表示为: (14) 式中:n为转速,r/min;z为叶片数;i为谐波序号,i=1为基频,i=2,3,…为高次谐波。 图6为叶片不同监测点处声压级随频率分布规律图。图(a)为4个噪声监测点位置,噪声监测点是以叶片气动中心(0,0,0.950R)为原点,依次取正x轴、正y轴、负x轴、负y轴r2=2 m处,由于在该展向平面的攻角为3°左右,可认为P1在叶片的尾缘处,P2在叶片的吸力面处,P3在叶片的前缘处,P4在叶片的压力面处。即监测点的坐标分别为P1(2,0,0.950R)、P2(0,2,0.950R)、P3(-2,0,0.950R)、P4(0,-2,0.950R)。图(b)为7 m/s风速工况下监测点的频谱分布图。从图中可以看出,声压级沿叶片气动中心一周的分布有所不同。在点P1、点P2和点P4处,噪声声压级频谱呈宽频特性,而点P3处呈低频特性,尤以锯齿型叶片的低频特性最为明显。点P3和点P4处声压级的主频为2.4 Hz,强度最大;高阶谐波频率次之,分别为4.8 Hz、7.2 Hz。 图6 监测点噪声声压级分布 图7为不同监测点处声压级频谱分布图。图(a)为5个噪声监测点位置,噪声监测点是以叶片气动中心(0,0,z)为原点,沿正x轴展向取r2=2 m,即5个点的坐标分别为(2,0,0.300R)、(2,0,0.467R)、(2,0,0.630R)、(2,0,0.800R)、(2,0,0.950R)。图(b)为7 m/s风速工况下的监测点频谱分布图。从图中可以看出,噪声声压级沿展向越靠近叶尖部分宽频分布规律越明显,且当展向平面r/R>0.467时,声压的主频和高阶谐波频率一致,分别为2.4 Hz、4.8 Hz和7.2 Hz。在展向平面r=0.300R处,风力机锯齿型与原型的声压频谱差别最大,且风力机叶片叶根处紊乱的流线使风力机原型已不再遵循主频规律。在展向平面r=0.467R处,两者的吻合度最高,r=0.950R监测点处吻合度次之。 图7 监测点噪声声压级分布 本文以NREL Phase VI风力机为主要研究对象,将 NREL Phase VI风力机叶片进行锯齿尾缘改造。运用数值模拟方法对整体叶片进行计算,研究7 m/s风速工况下的气动特性及噪声特性,主要得出以下结论: 1)NREL Phase VI风力机原型与锯齿型的主要差别出现在尾缘部分,该截面上锯齿结构改变了其压力性能。 2)在叶片吸力面靠近叶尖的尾缘区域,风力机原型相较于锯齿型出现了明显的分离现象,这表明锯齿结构改变了壁面的分离模式,使流场得到改善。 3)7 m/s风速工况时,在同一展向平面,与风力机叶片的距离越大,噪声声压级越小,基本与翼型声压级分布规律相吻合。锯齿型叶片声压级明显低于原型,证明了锯齿结构的降噪特性;且声压级在叶片前缘处较大、尾缘次之,这与锯齿尾缘改善了流动状态有关,同时也说明了风力机叶片前缘与尾缘是噪声集中产生的位置。 4)在叶片尾缘处噪声声压级频谱呈宽频特性,而前缘处呈低频特性,尤以锯齿型叶片的低频特性最为明显。尾缘声压级的主频为2.4 Hz,强度最大;高阶谐波频率次之,分别为4.8 Hz和7.2 Hz。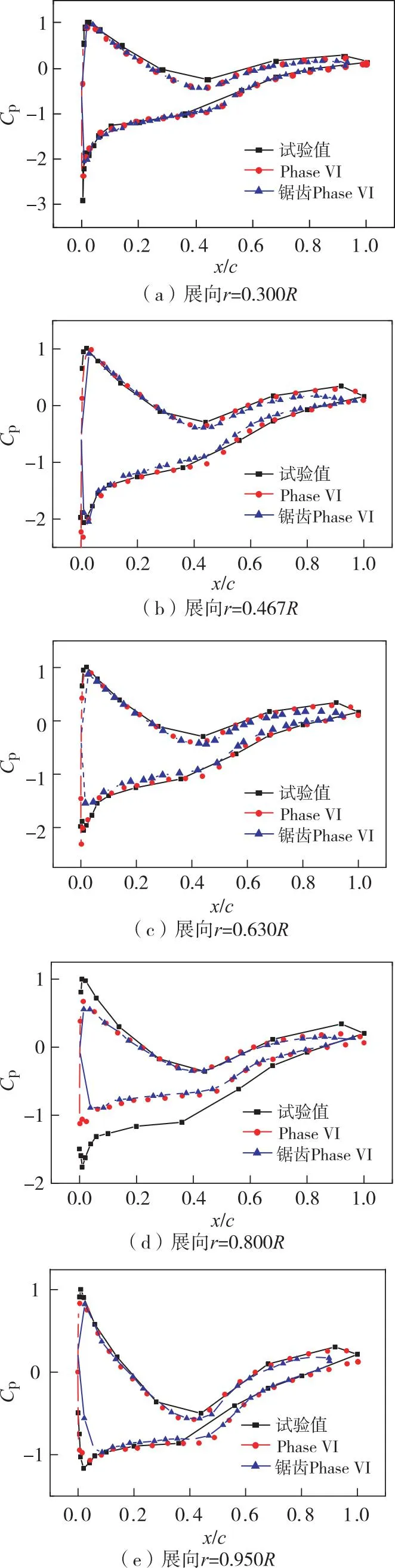

2.4 叶片噪声特性分析



3 结语

