基于数值计算和模型试验的泵站侧向进水结构优化
王 翌
(新疆水利电力建设总公司,新疆 乌鲁木齐 830091)
1 研究方法
图1所示为某泵站侧向进水结构的平面布局,图(a)和图(b)分别为该泵站的俯视图和A-A截面的视图;选用了UG的3D构造设计软件,并以1∶10的比例建立泵站侧向进水结构计算模型。

图1 泵站侧向进水结构的平面布局(单位:mm)
根据质量守恒、能量守恒和动量守恒定律,当流动介质为清水时,可不考虑温度变化,则连续性方程与质量守恒定律关系如式(1)所示[1-2]。
(1)

(2)
式中:ui为不同方向上的平均速度,m/s;xi为流体中某一点x方向上的动量分量,kg·m/s;μ为绝对黏度,Pa·s;τij为应力张量,Pa。湍流数值模拟使用Reynolds时均数模拟方法进行[3]。它可以有效克服计算量大的难题。
而湍流模型中,Realizable 模型由于能够完美地结合标准模型的特点,即能够计算近壁面处的黏性流动,又能准确地计算主流区附近的湍流,能够良好的捕捉到近壁面位置的涡结构,节省计算时间。因此,此次研究采用Realizable k-ε模型进行数值模拟,采用Fluent软件对其进行计算。利用二阶迎风进行离散,SIMPLEC算法求解,从而获得更高的计算效率。
2 泵站侧向进水前池多结构参数优化
在循环水泵机组中,由于侧向进水对水泵的抽水特性影响较大。故需优化侧向进水前池的结构,以改善水泵的抽水效率。通过试验研究,确定不同结构参数下进水流道内水流特性变化规律。由于响应面试验优化方法的测试时间更短,测试数量也更少,故可以在保证准确度的情况下,采用响应面法降低各因素的取值幅度,并对试验数据进行分析与讨论。以此优化各结构参数的最佳组合[4-5]。
考虑到扩散角α、坡度β、转向角γ对进水结构的水力性能影响较大,利用该三个参数作为优化侧向进水前池的参数,并将该三个结构参数当作响应面试验方法的自变量。同时,对该三个参数作三因素三水平试验,使用数值模拟的方法,对各个方案的侧向进水结构的流场进行模拟,以得到试验结果。
在此基础上,将所选择的影响因子与试验结果值进行比较,并将其与响应面优化模型进行比较,利用方差分析法,建立精确的试验数据及试验数据间的回归方程,从而实现回归模型的显著性判定[6]。在满足显著性指标的前提下,分析各结构参数之间的相互作用,探讨结构参数与优化设计指标之间的关系,得到能够提高出口断面流速分布均匀度的侧向进水结构参数。如果不能达到预期的效果,就会根据响应面方法的测试结果,反复进行以上的测试,直到达到预期的效果。
3 泵站侧向进水结构模型试验
按1∶10比例将优化后的模型开展不同条件下的泵站侧向进水流场试验,并将其与试验结果进行对比,对理论和试验结果的正确性展开验证。基于上述结论,本项目拟对不同工况下的泵站侧向进水流道进行相关试验。主要对优化后的泵站侧向进水结构内部水流特性,尤其是侧向进水池和进水流道内部流态等进行数值仿真。
该试验模型由引水段、侧向进水前池、进水流道和进水喇叭管等组成,且试验装置选用一台循环水泵作为电源。采用变频器控制循环泵的转速,进而对系统中的流量进行调整,并对不同管道的闸阀进行切换,实现了对水泵运行机组的顺序的控制,并保证了同一时间水泵均有相同的流量[7]。水流是使用循环水泵,通过输水管道输送至蓄水箱,之后再进入引水段。为了保证第二次进入引水段的流型稳定,引水段必须适当加长[8]。进水流道侧壁装有一块有机玻璃,可观察进水喇叭口的水流状态,也可便于转动度仪测量。在泵站侧向进水结构的测速剖面中,应用流速传感器进行流量测定,其误差值不能超过1%。使用丝线法,对侧向进水前池内的流态展开测量,丝线在侧向进水前池内摆动的水平投影方向应该不超过10°。
4 泵站侧向进水结构优化结果分析
4.1 原始模型数值计算结果
此次工程项目共有660 MW机组2台,每台机组配备3台立式固定叶混流循环水泵,3×50%的比例。循环水系统的运行方式为单元式,全负荷运行时,在考核的天气情况下,1机2泵同时运行,而1机1泵运行的情况,一般是在夏季低负荷或冬季中负荷的条件下。在“1机1 泵”和“1机2泵”两个工作状态下,采用了不同的设计方案,提出了12个不同的水位条件下的计算方法。在设计操作水位的原始模型中,对各种机组运行方案进行了计算,结果如表1所示。
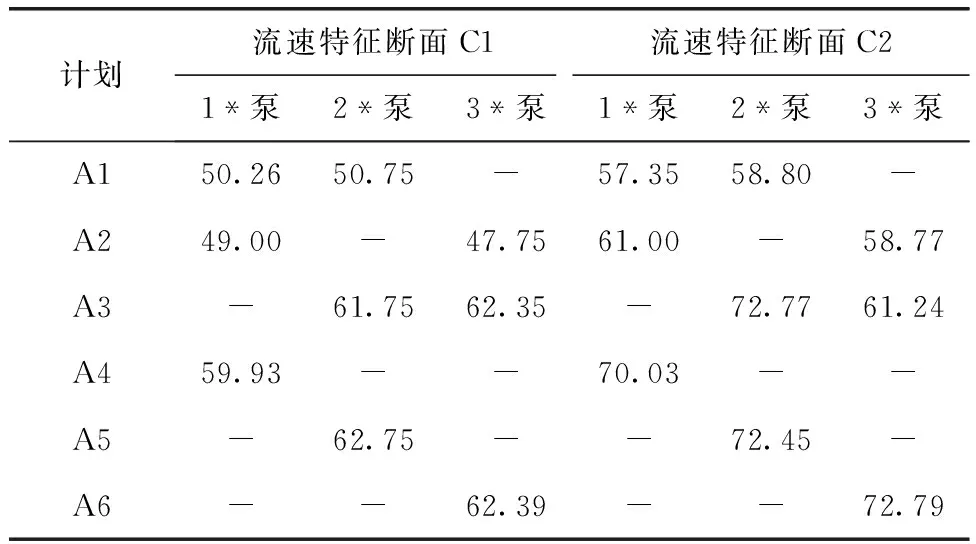
表1 设计运行水位不同机组运行方案C1和C2断面流速分布均匀度 %
由表1可以看出,在设计运行水位条件下,C2断面上两台水泵在不同工况下的流速分布均匀度较低,说明两台同时运行时,每个机组进入进水流道前,两台水泵间存在主流之间的干扰,使得两台水泵前池的流态比单台水泵较差。并且在不同的运行水位状态下,每个方案的特征断面流速均表现出较低的分布均匀度,且每一段的流速也不均匀。在A2工况中,1*泵的进水流道流速分布均匀度只有49.00%,3*泵为47.75%,这不能满足进水流道的速度要求,也不能保证进水流道的流动一致,并可能出现倒灌和漩涡等现象。
设计运行水位下每个水泵机组在流道出口断面处的速度分布一致,整体上表现为中部流速大,周围速度小。但在机组运行方案下,中间高流速区域与中心位置均发生了偏离,使得循环水泵的进水条件有所下降。
由表2可以看出,在每个机组的运行计划下,每个进水流道出口段的平均加权偏流角是65.73°,基本上达到了水力设计的要求。
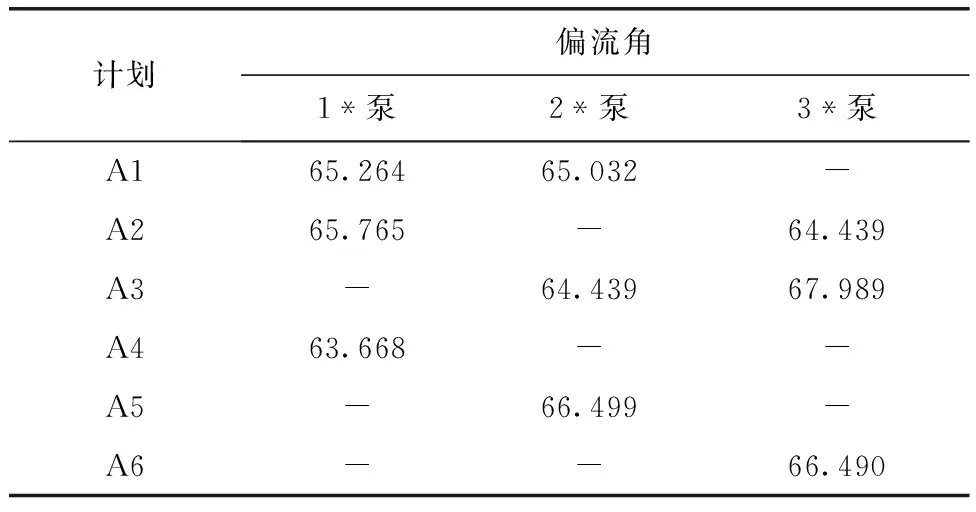
表2 设计运行水位不同方案流道出口断面流速加权偏流角 (°)
4.2 优化后侧向进水结构数值计算结果
为了优化侧向进水前池的不同结构参数,运用响应面法,进而得到以最佳流速分布均匀度为目标的数学模型的有关参数。通过对试验结果的分析,确定了优化后最佳的坡度、转向角和扩散角分别为8°、75°和11°。经改进后,侧向进水前池与进水流道在各种工况下的流动状态均优于原有模型,且无显著的偏流与大面积的回流漩涡;同时,在喇叭管附近,也并没有产生高强度的漩涡结构,在设计运行水位优化模型中,根据数值模拟的结果,对不同的机组操作方案进行了计算,并对流速特征断面C1和C2流速分布均匀度进行计算,结果如表3所示。

表3 设计水位不同方案流速特征断面C1和C2流速分布均匀度 %
通过表3可以看出,在特征断面C2上,流速分布均匀度较原设计有较大改善,改善幅度约为19.15%。计算结果显示,和原模型相比,优化后的模型能对侧向进水前池内已有的非理想流态进行调整与改善,从而提高了每一断面的流速分布均匀度。
不同机组在流道出口断面的速度分布比较一致,整体上表现出中部速度大,周围速度小的特点。对优化后模型的进水流道出口断面加权偏流角平均值进行计算,结果如表4所示。

表4 设计运行水位优化模型不同泵组合流道出口断面流速加权偏流角 (°)
由表4可以看出,在不同的运行方案操作模式下,所有机组在进水流道出口处的平均断面加权偏流角是78.44°,比原来的模型增加12.93°。
4.3 泵站侧向进水结构模型试验分析
在A1工况下,对优化模型的测速断面C1处的每一个测点进行流速测试,计算出流场的流速分布均匀度,并将其和数值计算进行比较,检验数值计算方法的准确性。对A1工况下优化模型特征断面C1处的流速分布情况进行分析,其中,A1工况1*泵的测速断面C1纵向测点流速如图2所示。

图2 A1工况1*泵的测速断面C1纵向测点流速
图2中,数值计算结果流速的横向变化趋势与模型试验结果相吻合。在1*泵C1断面上,多数测点负横向流速比正向流速大,主要原因是在进水流道入口附近,在转向段的影响下出现了偏流。同理,A1工况2*泵的测速断面C1纵向测点流速如图3所示,图3中,数值计算结果流速的横向变化趋势与模型试验结果同样相吻合。在特征断面2*泵C1段,多数情况下,纵向侧面负横向流速与正向流速接近;当处于进水流道段时,水流的流向基本上与入口段相一致,没有出现显著的偏流。对数值计算和模型试验的断面C1的流动速度分布均匀度进行分析,结果如表5所示。

表5 A1工况下特征断面 C1 流速分布均匀度 %
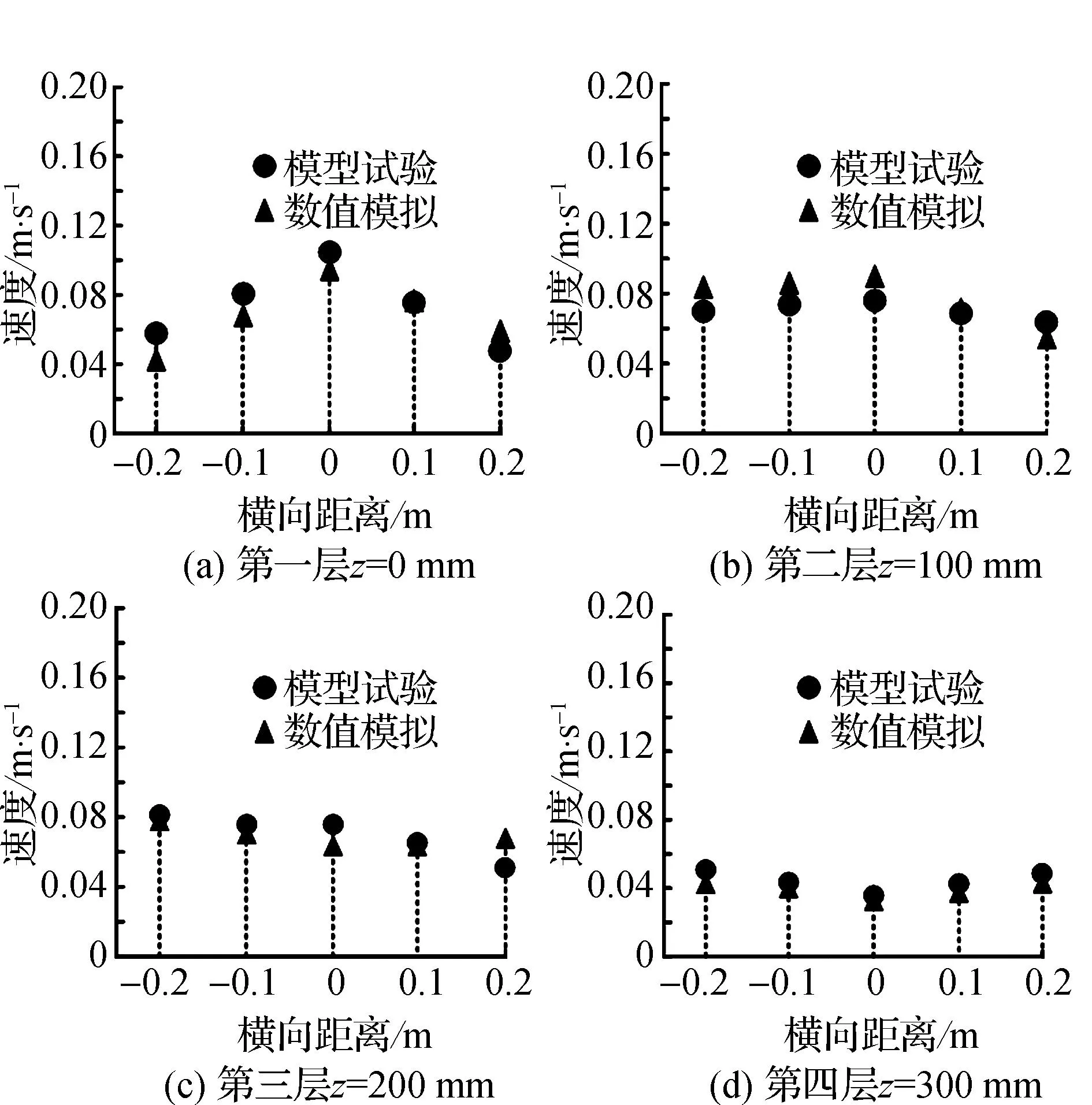
图3 A1工况2*泵的测速断面C1纵向测点流速
通过表5可以看出,模型试验和数值计算对1*泵和2*泵的结果比较接近,且1*泵和2*泵的相对误差值都在5%之内,分别为4.39%、4.82%。
5 结 论
为了使水流能够在泵站的进水前池中均匀地分布,并无大范围的回流、漩涡等现象。通过数值模拟、模型试验等手段,对泵站侧向进水结构中的水流形态及水力特征进行深入的分析,用响应面对原有的模型结构参数进行了优化。并通过试验进行验证。表明研究成果对类似侧向进水结构的泵站水力设计和水力特性的优化有一定的借鉴意义。但由于影响侧向进水结构内流动状态的因素众多,后续将对侧向进水结构内水流状态的变化规律进行深入研究。

