基于改进支持向量机的LCD液晶屏气泡分类识别

王曙敦，贺 杰

(深圳晶华电子股份有限公司,深圳 518000)

液晶显示屏不仅给人们带来了良好的视觉感受,也让任何时间地点的信息交互变成现实,现代科技的进步也迈上了万物互联的新台阶。作为信息交互的重要组成部分,液晶显示屏的应用前景非常广阔[1-2]。LCD显示屏是一种最常用的液晶显示屏,因其生产成本低廉,响应时间较快,目前已成为中低端现实市场的主流产品[3-4]。液晶显示屏的质量问题主要分为两类:一类是画质类问题,另外一类是功能性不足。其中,画质类问题大多由于线路不良引起,通过更换电路板等方式即可恢复。气泡类故障是最常见的功能性问题,此类故障产生原因相对复杂,通常无法进行维修[5]。因此对LCD液晶显示屏的气泡分类进行研究,提高液晶屏气泡分类识别的正确率,对于及时发现液晶屏的质量问题具有重要意义。

1 构建训练样本

1.1 基于轮廓面积的气泡

液晶气泡边缘通常为封闭曲线,而气泡背景大多是点线轮廓,封闭曲线的面积采用格林公式进行计算,在此基础上对各轮廓面积进行比较,找出其中的最小值,即可完成气泡标注。

格林公式的基本原理如下:令光滑曲线闭合区域上的连续函数为P(x,y)和Q(x,y),它们都具有连续一阶偏导,则:

(1)

式中:D为曲线闭区域;L为D的边界。

令P=-y,Q=x,则可以得到

(2)

由此可以计算出D的面积S为:

(3)

由式(3)可知,如果轮廓为直线或者是零,则S=0;对于气泡而言,其轮廓为封闭曲线,因此S>0。

本文采用Python软件对曲线的轮廓面积进行计算,为了避免在计算过程中受到噪声点的干扰,将筛选阈值设置为6像素。

采用外接矩形框将筛选结果中的气泡位置框出,这样可以将屏幕中82%的气泡标注出来,其余气泡则需要进行人工标注。

1.2 构建正负样本

气泡被标注后,其标注文档中就会有该气泡的相关边框信息,具体如图1所示。采用Python软件进行批量剪裁,其中,可以直接提取的气泡图像为正样本,随机剪裁的非气泡部分为负样本。

图1 标注文档部分信息截图

2 QPSO-SVM分类器

2.1 支持向量机

支持向量机(Support Vector Machines,SVM)是由Vapnik等人基于统计学习理论提出的一种机器学习方法,SVM处理非线性分类、回归问题的原则是将低维空间的复杂数据通过核函数映射到高维空间,在高维空间中构造最优超平面进行分类、回归,从而使问题得到简化,降低计算的复杂程度[6]。

SVM最优超平面构造示意图如图2所示,令H为最优超平面, H可将图中的数据分为两类,此时可以得到另外两个超平面H1和H2,它们均与最优超平面H平行,H1、H2上的数据到H的距离最近,这些数据就是所谓的支持向量。

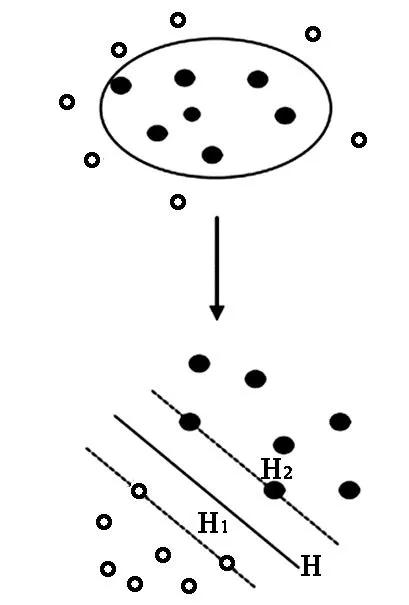
图2 SVM最优超平面构造示意图

支持向量机具有如下优点:

1) 对样本容量的要求较低,即使小样本也能获得较理想的计算效果;

2) 求解的思想是转化为二次规划问题求解,理论上确保全局最优解是存在的;

3) 计算结果只受支持向量的影响,降低了计算维度;

4) SVM的决策函数比较简单,简化了计算过程。

支持向量机分类原理如下[7]:令样本集为{(x1,y1),…,(xi,yi)}(xi∈Rn,y∈{-1,1}),高维空间超平面的方程可表示为:

wT·x+b=0.

(4)

式中:w为权向量;b为偏置量。

为了使样本集到超平面的距离最小,令判别函数f(x)=wT·x+b,且有xi∈Rn,|f(x)|≥1,则距离最小时有:

(5)

约束条件为:

y·(wT·x+b)≥1.

(6)

当样本集中元素满足yi·(wT·x+b)=1,这些元素即为支持向量,其余元素与超平面之间距离>1,该距离为2/‖w‖。

为了计算w和b,引入拉格朗日函数,则有:

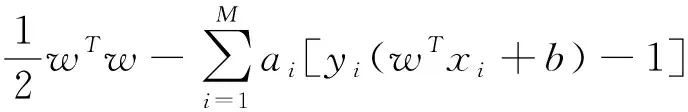
(7)

式中:ai(ai>0)为拉格朗日系数。

对式(7)中的w和b求导:

(8)

(9)

求导后可得:

(10)

将式(10)转化为二次优化问题,可得:

(11)

求解式(11),得到下列线性分类判别函数:

f(x)=sign(wT·x+b).

(12)

对于分类问题,SVM的求解思路是采用非线性函数将样本数据映射到高维空间,在高维空间建立分割超平面进行分类,为了使函数的推广能力和经验风险之间得到平衡,可以引入非负的松弛变量ξi,此时相应的约束条件变为:

s.t.y·(wT·φ(x)+b)+ξi≥1;ξi≥0 .

(13)

同时引入惩罚项,则有:

(14)

式中:C为惩罚参数,C>0。

则欲求解的问题变为:

(15)

引入核函数k(xi,xj),即可得到SVM分类判别函数:

(16)

常用核函数有多项式核函数、线性核函数和径向基核函数,为了提高SVM分类的准确性,本文采用径向基核函数,其表达式为:

(17)

式中:σ为核参数。

SVM的回归效果受惩罚因子C与核参数σ的影响很大,为了提高SVM拟合精度,需要对C和σ进行寻优。

2.2 量子粒子群算法

量子粒子群算法(Quantum Particle Swarm Optimization,QPSO)是基于PSO算法提出的一种改进算法,它认为粒子群在寻优过程中遵循量子力学[8]。在QPSO算法中,粒子能够实现整个可行解空间的搜索,且QPSO算法只有位置一个控制参数,其优化性能比PSO算法更好。QPSO算法的粒子采用薛定谔方程ψ(x,t)进行描述,然后利用蒙特卡洛模拟得到的粒子位置,具体如下:

(18)

式中:u为随机数,u∈[0,1],其值服从正太分布,pid(t)、L的值可根据下列式子确定:

(19)

(20)

pid(t)=φ·pid(t)±(1-φ)·pgd(t).

(21)

(22)

式(19)～式(22)中:M为粒子个数;D为维数;φ为随机数;φ∈[0,1],其值服从正太分布;pid(t)为第i个粒子在第t次迭代时的最优位置;pgd(t)为所有粒子在第t次迭代时的最优位置,为有粒子在第t次迭代时最优位置的平均值;β为收扩系数;m、n为收扩系数参数。

综合式(9)～式(12),得到QPSO算法粒子位置的更新方程为:

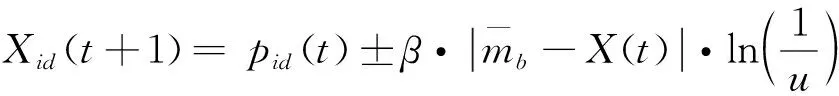
(23)

式中:当β≤0.5时,式(23)中的“±”取“-”,当β>0.5时,式(23)中的“±”取“+”。

相比PSO算法,QPSO算法既保留了PSO算法良好的优化性能,又简化了粒子寻优方式,操作更简便,且具有更强的全局收敛能力,目前在能源、交通、医疗等领域得到了广泛应用。

2.3 QPSO-SVM液晶气泡分类识别模型

采用QPSO算法对SVM的惩罚系数C和核参数σ进行优化,对支持向量机进行改进,建立基于改进支持向量机的LCD液晶屏气泡分类识别模型,建模流程如图3所示,建模步骤如下:

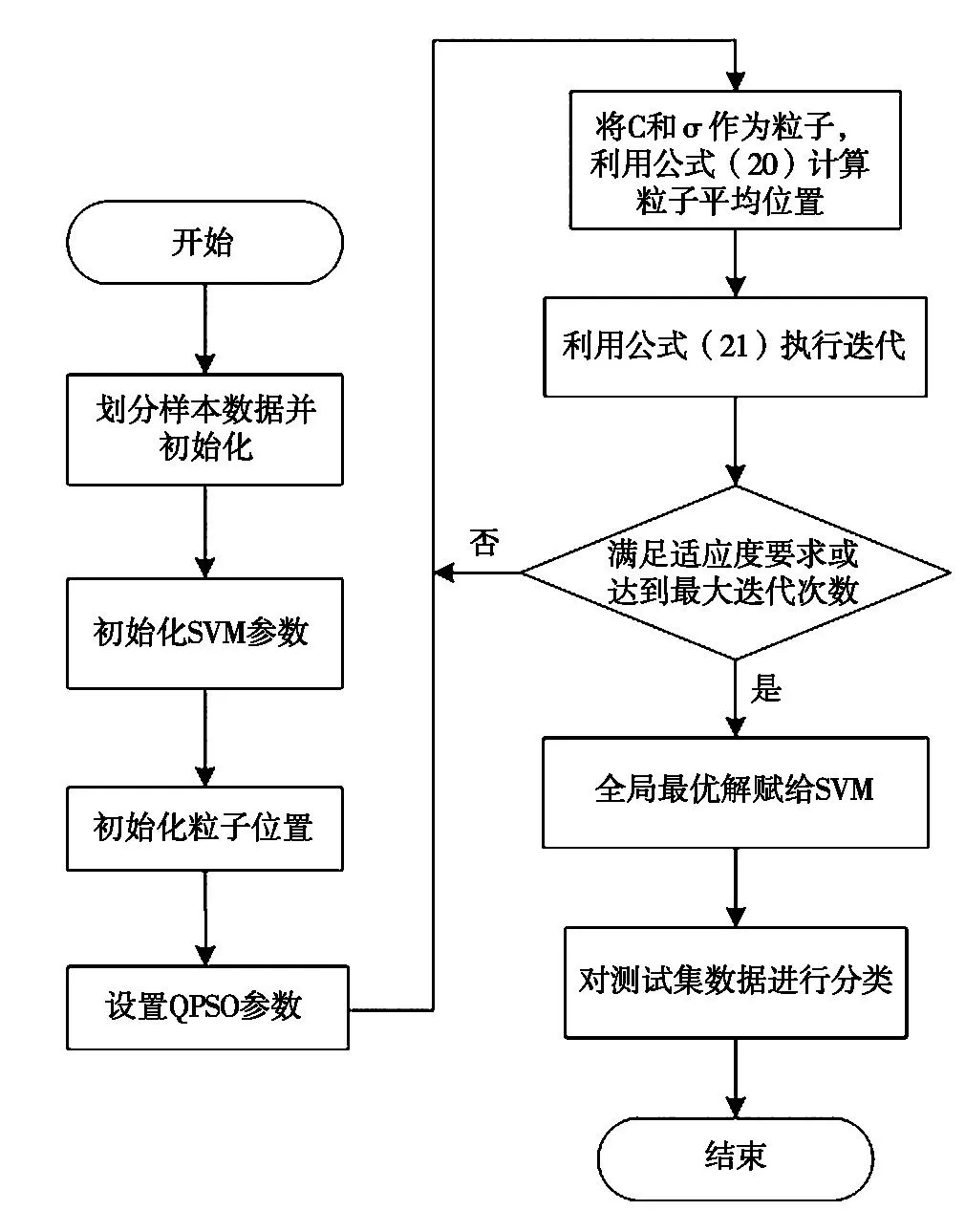
图3 模型流程图

1) 划分样本数据并初始化,将样本数据划分为训练集和测试集,并初始化气泡样本数据。

2) 初始化SVM参数,设置惩罚系数C和核参数σ的初值及搜索范围,计算初始适应度值。

3) 初始化粒子位置并对QPSO算法的相关参数进行设置,主要空间维数、粒子数目、最大迭代次数和收扩系数参数等。

4) 将C、σ作为粒子,利用公式(20)对所有粒子的平均最优位置进行计算。

5) 利用公式(21)执行迭代,对粒子当前适应度值进行计算,并与上一次的适应度值比较,如果优于,则进行替换,否则保持不变。

6) 确定种群最优适应度值,并与上一次的种群最优适应度值比较,如果优于,则进行替换,否则保持不变。

7) 利用公式(23)更新所有粒子的位置。

8) 判断迭代结束条件是否满足,若满足,则输出惩罚系数C和核参数的最优解,否则,返回步骤5)。

9) 将最优解赋给SVM,对测试集中液晶气泡进行分类。

3 仿真分析

3.1 QPSO-SVM模型分类结果

采用Python软件进行批量剪裁,构建仿真分析中所用的样本数据,将样本数据划分为训练集和测试集,它们分别用于模型的训练和检验分类效果,训练集和测试集的样本组成情况如表1所示。

表1 训练集和测试集的样本组成情况

采用下列四种常用指标对分类器的分类效果进行评价,它们分别为:

1) Accuracy:表示分类结果的总体正确率,主要用于衡量分类器的总体分类效果。

2) Recall:表示查全率,分类正确的气泡数量占总气泡数量的比重。

3) Precision:表示查准率,主要用于评价分类结果正确的样本占总样本的比重。

4) F1:表示查全率和查准率的平均值。

采用训练集数据进行训练,利用QPSO算法对SVM的惩罚系数C和核参数σ进行寻优,寻优结果为C=37.24和σ=6.35,将最优解赋值给SVM,利用改进支持向量机分类器对测试集样本进行分类,表2给出了改进支持向量机的分类结果指标。为了对比分析,采用支持向量机和随机森林两种常用的二分类方法对测试集样本进行分类,分类结果的各项指标也如表2所示。

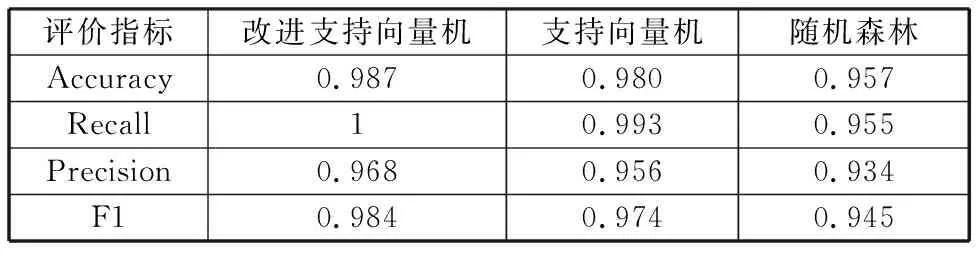
表2 三种分类器分类结果的各项指标

对比表2中的三种分类器的各项指标数据可以看出,本文所提改进支持向量机分类器的分类效果更好,验证了本文所提LCD液晶屏气泡分类识别方法的正确性和优越性。

3.2 工程应用分析

气泡分类完成后,利用滑动窗口法对LCD液晶屏幕上的气泡进行检测,提取其中的灰色部分。选取200个LCD液晶屏幕进行测试,屏幕中共有气泡250个,检测结果及检出率计算结果如表3所示。

表3 检测结果及检出率计算结果

从检测结果上看,本文提出的基于改进支持向量机的LCD液晶气泡分类方法具有良好的识别效果,对于边缘受遮挡和对比度较低的屏幕,都能够被正确识别出其中的气泡。

经检查发现,未检测出的气泡主要有两种:一种是气泡形状不完整,此类气泡通常由很多小气泡聚集而成,其边缘信息相对特殊,模型无法正确识别;另一种是气泡体积过小,通常都在2 mm以下,此类气泡的边缘信息无法正确提取。

4 结论

本文采用量子粒子群算法对支持向量机的惩罚参数和核函数进行优化,建立基于QPSO-SVM的LCD液晶屏气泡分类识别模型,采用LCD液晶气泡数据进行算例分析,并与其他二分类方法的分类效果进行对比,结果表明,QPSO-SVM分类器的分类准确率高于其他方法,验证本文所提LCD液晶屏气泡分类识别方法的正确性和实用性。