改进的边缘计算和全生命周期的排水管网监测方法*

韩丽明，张艳玲，赵 瑶，刘林越

(1.西安工业大学 电子信息工程学院,西安 710021;2.西安工业大学 计算机科学与工程学院,西安 710021)

在智慧城市的建设中,城市排水管网的智能监测体系的构建是智慧城市的重要组成部分,其中智慧管网中水情和井盖状态的监测是重中之重。管网异常无法发现,不仅会发生溢流的情况,还会严重危害人员生命安全,给社会带来非常大的生命财产损失[1-2]。

由于管网环境的恶劣性,传统的管网监测方法存在极大的误差,并且由于管网监测节点一般都采用电池供电,随着时间的变化,监测节点生命周期后期由于电池电压衰减导致监测数据传输丢包率增大,甚至停止工作。目前针对上述问题有以下几种解决方案:1) 通过能量采集来补偿电压,文献[3]利用温差能量来实现胎压的全生命周期监测,文献[4]利用风能为环境监测系统供能,延长其生命周期,文献[5]利用钹式压电发电来为智能井盖提供全生命周期能量;2) 采用多传感数据融合的方式节约节点能量,从而降低电压衰减并提高监测精度,文献[6]采用一种分布式传感器管理算法来降低传感器网的负载,文献[7]通过多传感数据融合来减小电压衰减,延长传感网的生命周期,文献[8]通过融合温湿度传感器数据,降低了电压对温室监测系统的影响,提高采集精度;3)使用低功耗的传感网和降低数据采集频率的方式来减小监测节点生命周期内的电压衰减,文献[9]、文献[10]通过降低采集频率来对环境进行长期监测。这些方法虽然一定程度上提高了监测精度,并降低了电池电压衰减对监测生命周期的影响,但鲁棒性很差,受工作环境尤其是温度和海拔的影响较大。

本文根据井下环境的特性[11-13]以及实现全生命周期高精度监测的目标,对监测误差来源进行分析,构建反射式超声测距误差补偿模型与基于Manony滤波算法的管网井盖姿态解算模型,以提高测量精度;引入边缘计算,以降低云端的数据压力;通过研究电池电压衰减对监测节点的影响,设计双电源稳压平衡电路,对GPRS模块进行单独稳压供电,以期解决传统电源供电下电压衰减导致监测不稳定以及鲁棒性差的问题,实现对排水管网全生命周期监测。

1 边缘计算和全生命周期的排水管网监测方法

所提出的排水管网监测方法具体步骤为

① 数据采集:使用超声波和陀螺仪对管网水位和井盖姿态进行监测;

② 边缘计算:对超声波进行温度补偿计算,对陀螺仪的6轴加速度与角速度数据进行姿态解算;

③ 数据传输:将监测的管网数据通过GPRS无线通信上传到云平台服务器进行存储展示;

④ 云平台接收:云平台选用ONENET平台来实现监测数据的存储、展示以及告警信息的推送;

⑤ 异常告警部分:当数据异常时,在上位机端显示告警信息,并推送邮件告知相关人员,同时在下位机端进行声光告警提醒过往行人车辆;

⑥ 双电源稳压:设计双供电稳压电路,对GPRS模块进行单独供电,采用稳压模块对电源输出的电压进行控制,保证输入GPRS模块的电压不会随着时间的推移发生电压不足的情况,从而增加了模块的稳定性。监测过程如图1所示。

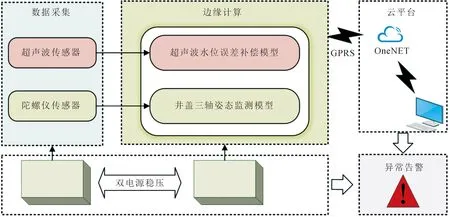
图1 基于边缘计算和全生命周期的排水管网监测流程

2 反射式超测距误差补偿与三轴姿态解算模型

2.1 超声波测距误差分析及建模

2.1.1 超声波误差分析

超声波频率较高,在直线方向上有着很强的传播能力,传输过程中衰减比较小,并且受介质的干扰较小,因此其传播距离非常远;同时超声波监测功耗很低,正常工作电流在2 mA以下,配合休眠模式的使用,功耗能进一步降低,有助于监测节点的全生命周期监测,非常适合在户外恶劣坏境下进行全天候的长距离监测;并且利用超声波来监测管网的水位,精度要高于传统的红外测距[14]。

超声波测距分为直射和反射两种[15],由于管网水位监测依靠水面反射声波来进行距离的监测,直射式超声波其工作方式需要在测量的起点和终点分别安装一个超声波探头,并不适合排水管网的水位监测,因此本文采用反射式超声波测距,反射式超声波测距的工作原理如图2所示,图中d为探头到水面的距离、H为探头到水底的距离,h为水深。

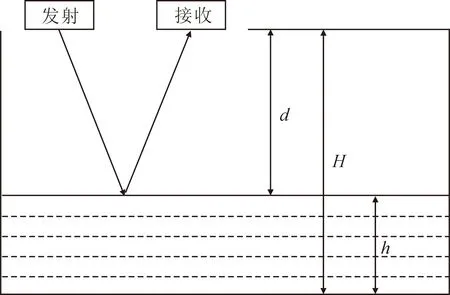
图2 反射式超声波测距原理

声波发射后定时器开始计时,当声波遇到水面反射回发射位置时,捕获口捕获到回波信号,定时器停止计时,记录的这一段时间为声波发射到返回的时间。初始化后,再一次发射声波,判断回波是否到达。管网井盖到水面的距离为

(1)

式中:d为测量的距离;t为声波从发射到返回的时间;v为声音在空气中的传播速度。但是由于水面与空气属于不同介质,导致v在实际应用中并不是一个常量,这是因为超声波在介质中传输会产生部分衰减,导致超声波实际传播速度与介质的弹性模量存在一定的函数关系[16],为了描述上述特性,引入一个传播常数为

(2)

式中:ω为角频率;c为平面行波中的相速度;a为衰减常数,故排水管网的超声波的声学特性可以用c和a来描述,这两个量为频率、压力和温度的函数,其中,排水管网的液体为单一介质水,超声波在水中的声学特性几乎不受频率变化,而排水管网的预埋深度严格遵守国家相关标准,其深度对排水管网水位监测影响为单一误差,故不考虑管网深度对超声波测距的影响,将不同地区之间的气压差距作为压力误差的主要来源;温度方面,主要受a的影响,a与介质的热传导性有关,与频率的平方成正比,因此在排水管网监测中可以用a/f2和c来描述超声波在排水管网中不同温度下的声学特性。综上,可以建立排水管网中超声波速度与温度、气压之间的关系为

v=∑i,jYijTipj=Y00+Y10T1+Y20T2+…+Y01p1+Y11T1p1+Y21T2p1+…+YijTipj,

(3)

式中:Yij为介质的非零系数,水的非零系数见表1,T为温度,p为管网所在地区大气压强,v为超声波速度。为了便于后计算,文中在p为一个标准大气压,即P=101.325 kPa的条件下进行后续建模仿真。当水温T为0～100 ℃、气压P=101.325 kPa时,水温T与超声波传播速度v的关系,以及水温T<40 ℃时的线性拟合关系如图3所示。

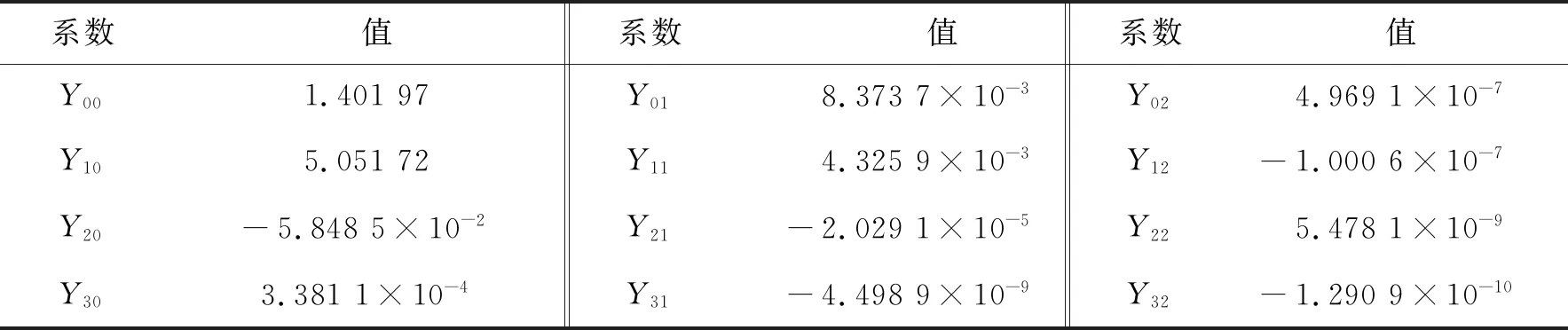
表1 水的非零系数

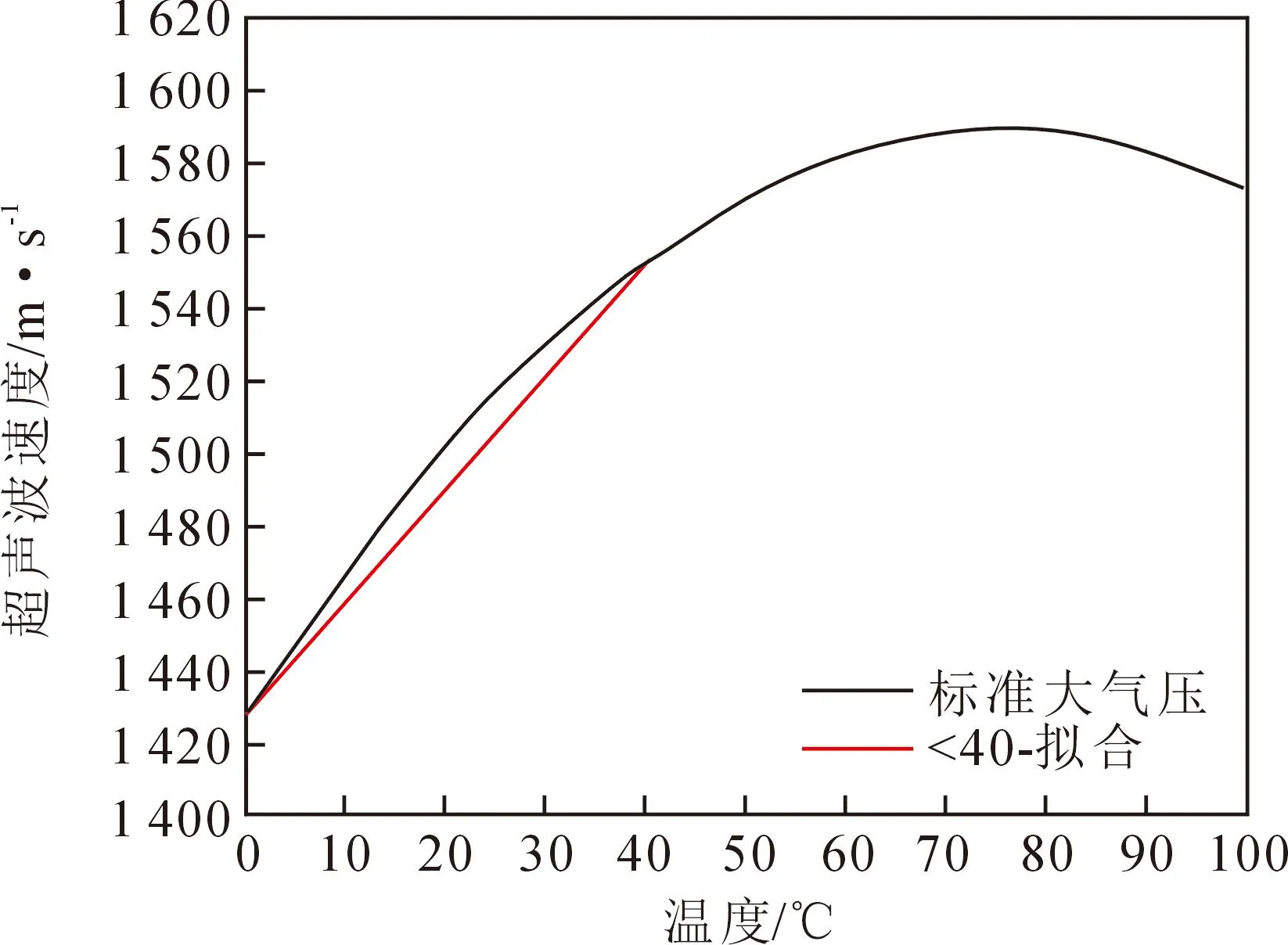
图3 超声波传播速度与温度的关系

由图3可以看出,在温度高于40度的情况下,压强为一个标准大气压的时候,温度对超声波速度的影响程度逐渐减小,将表1中非零系数以及标准大气压式带入到式(3)中,由于T4项以后对于排水管网的监测影响小于0.002 m·s-2,因此忽略不计,可以得到超声波在介质中的传播速度与温度的关系如下

v1=1401.97+5.4886T-6.0479×10-2T2-3.3634×10-4T3,

(4)

式中:v1为超声波在介质中的传播速度;T为介质当前的温度。

2.1.2 误差补偿

对于管网监测中的实际情况,不同管网的温度、压强往往都不同,由于管网深度都遵循同一安装标准,因此实际监测中不同管网的压强主要与当地所处海拔高度有关,故在误差补偿中取管网当地所对应的大气压作为压强参数,为了更加准确并节约能耗,大气压强通过调用中国气象站提供的测量数据获得;而温度不仅与季节有关,还与日夜间、以及排水管网的所处位置有关,因此温度通过监测节点上的温度传感器进行实时采集,以此来保证误差补偿的准确。

由式(3)可知,当超声波的传播介质为水的时候,超声波的声速与水的温度呈正相关,实际应用中,在温度小于40度并且海拔低于2000米的情况下,压力几乎对管网监测无影响,为进一步节约能耗,可以不用考虑海拔的影响,因此超声波传播速度在要求不高的常规管网环境下如图3所示可以拟合成线性方程进行误差补偿,线性方程如下

v=3.15T+1428,

(5)

则实际水位应该为

(6)

而对于特种、高海拔地区管道情况,超声波管网水位监测,应采用动态误差补偿,当温度大于40的时候,对监测结果采用式(5)进行误差补偿,对于压强的影响。则采用如式(3)所示的误差关系进行误差计算,则实际测量距离如下

(7)

2.2 基于Manony滤波算法的管网井盖姿态解算模型

2.2.1 四元数的测量

陀螺仪可以监测井盖姿态三个轴向的加速度和角速度,通过姿态解算可以反应出井盖的姿态变化。其硬件DMP可以将测得的角速度和加速度数据转换为4元组数据输出[17];陀螺仪与MCU通过IIC建立通信以后,会将DMP解算后的4元组数据传输到MCU中进行处理,通过下列公式可以将4元组数据进行计算从而得到欧拉角(俯仰角、横滚角、航向角):

(8)

式中:q0,q1,q2,q3为四元组数据,且四元组数据的平方和为1。

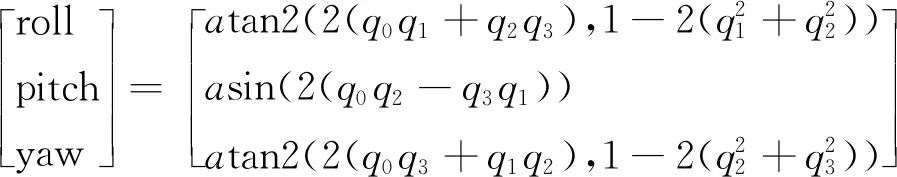
(9)

式中:roll为横滚角;pitch为俯仰角;yaw为航向角;q0,q1,q2,q3为四元组数据。

2.2.2 一阶龙格库塔法更新四元数

由于需要动态的对管网井盖姿态数据进行监测,因此需要对式(9)计算出的欧拉角进行实时更新,由于陀螺仪测量的原始数据为井盖三个轴向的角速度与加速度,故可利用测量的角速度来更新欧拉角,本文利用一阶龙格库塔法[18]对四元数的微分方程进行求解,一阶龙格库塔法方程如下

(10)

由上文可知四元数向量为Q=[q0,q1,q2,q3],将其带入式(10)所示的一阶龙格库塔法方程可得

(11)

式中:Δt为陀螺仪的测量时间间隔,从而进一步计算出对Q的时间导数如下

(12)

式中:ω为机体坐标系下的角速度,即陀螺仪的测量值;ωb为导航坐标角速度,根据一阶龙格库塔法,可以得到四元数的更新方程如下

(13)

上述四元数更新方程可以实时的更新陀螺仪测量的四元数,但是随着测量时间的增长,陀螺仪的实测数据会不断累积积分误差,会增大测量误差,因此本文利用Manony互补滤波算法做进一步的误差补偿。

2.2.3 Manony互补滤波算法

由于陀螺仪在长时间的测量中会不断累积积分误差,而MPU6050自身配置有一个加速度计,可以实时采集管网井盖运动的加速度,因此,为了纠正长时间测量的累积误差,采用Manony滤波算法将管网井盖水平面的加速度与重力进行对比、补偿,从而对陀螺仪测量过程中的积分误差进行弥补,具体过程如图4所示。

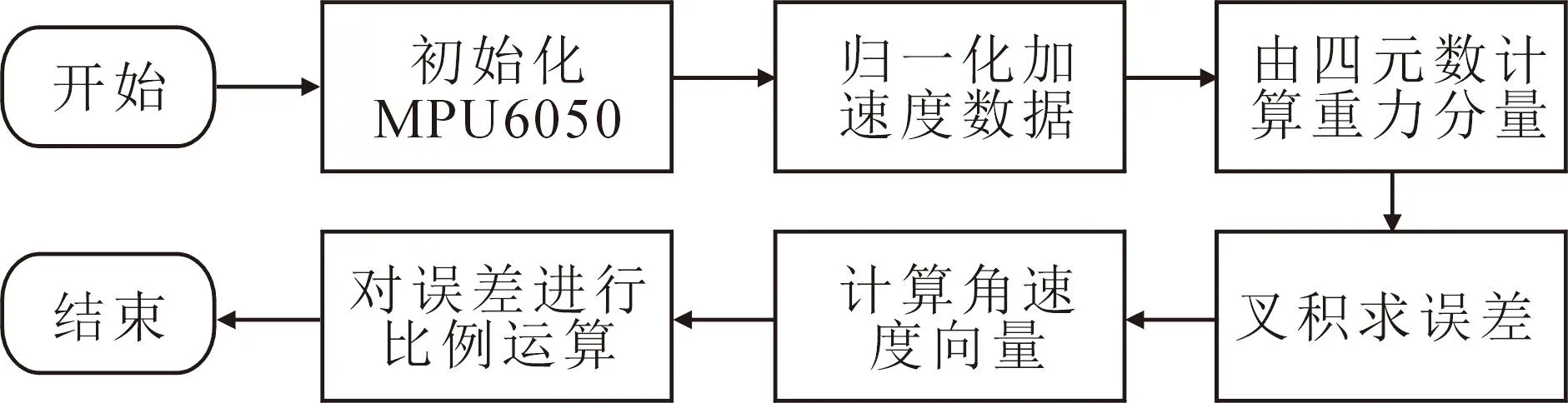
图4 Manony滤波过程

综上所述,利用上述方法可以极大的提高井盖姿态监测的精度,并且能够显著降低功耗,增加监测终端的续航,从而实现对管网的全生命周期监测。

3 边缘计算终端

管网监测往往有着节点数量庞大,监测数据量巨大,云端计算压力大的“三大问题”,而传统的监测方法通常采用“采集-传输-计算”的监测模式,这就导致后期的计算量压力非常大,为了解决这一难题,文中引入了边缘计算,极大的降低了数据的传输量,提高了管网监测的效率,边缘计算终端主要由数据输入,模型计算,误差补偿,结果输出,数据发送几部分组成,如图5所示为边缘计算终端的工作流程。

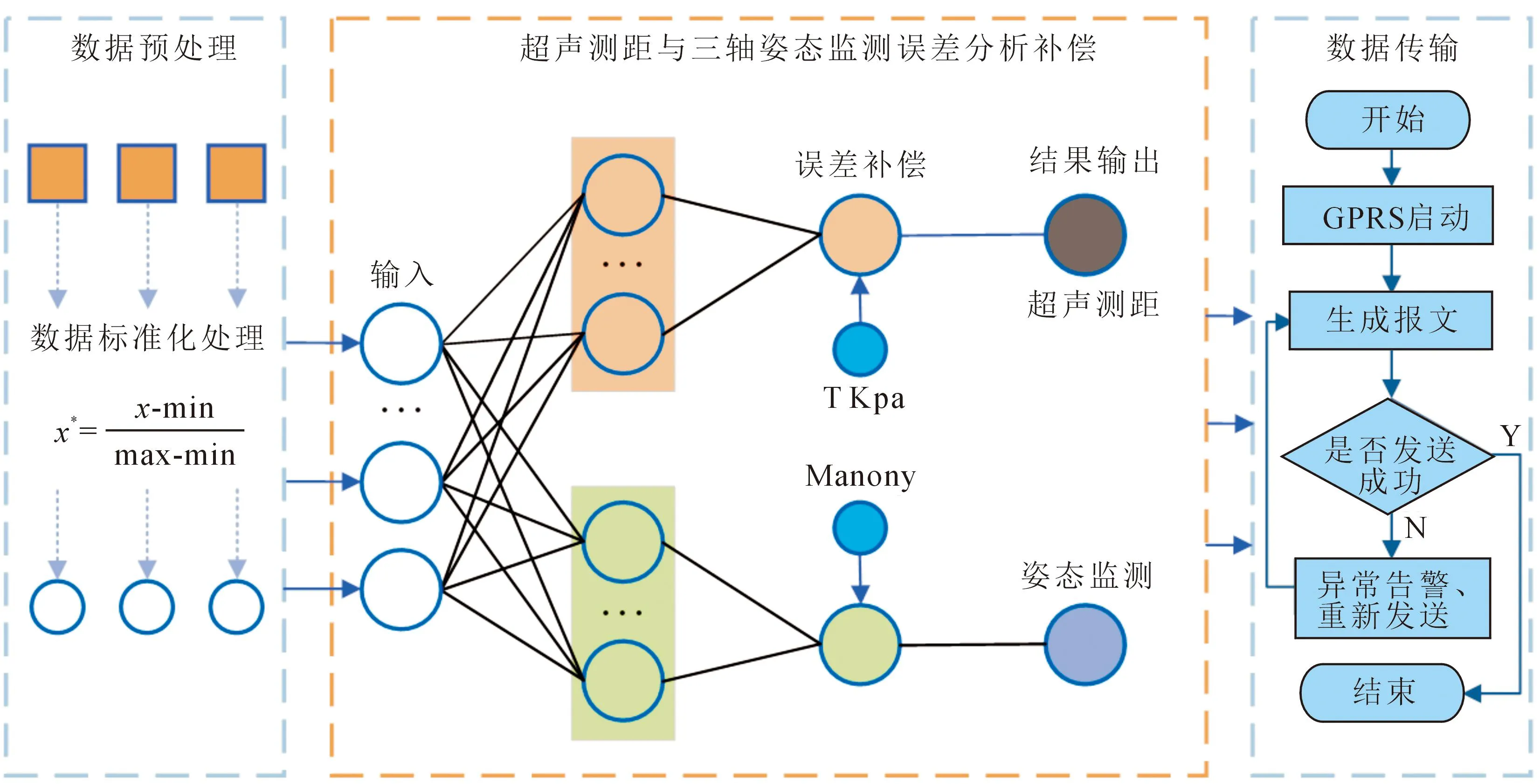
图5 边缘计算终端工作流程

终端利用超声波和陀螺仪对管网的水位和井盖姿态数据进行采集,并将数据传输到主控进行边缘计算,首先对原始数据进行归一化操作,去除离群值,然后将处理后的数据输入到反射式超声波误差补偿测距与三轴姿态监测模型中进行误差分析和误差补偿,以矫正传感器监测过程中产生的误差,提高监测精度,最后将经过边缘计算处理过的数据通过无线通讯传输到云端,终端各部分具体构成如下。

1) 边缘计算MCU:以STM32F103C8T6作为监测节点的MCU,用于监测节点数据的边缘计算处理。MCU分别以I2C和SPI协议接收超声波和陀螺仪采集的数据,并在本地进行误差分析、误差补偿后,将最终的监测数据通过UART传输到无线通信模块再发送到ONENET云平台上[19]。

2) 数据采集:通过HC-SR04以反射式测距方法对管网水位进行测量,使用MPU6050对管网井盖姿态的加速度和角速度进行测量,如图6(a)所示为HC-SR04电路图。通过MPU6050采集井盖姿态数据,它内部具有一个1KB的FIFO寄存器,能够缓存收集到的数据。只有当数据达到设置的阈值或者FIFO溢出(FIFO overflow)时才会触发MPU6050的中断系统,当再次静止时,陀螺仪加速度计的数据会达到寄存器ZRMOT_THR的静止阈值,MPU6050退出中断再次进入低功耗模式[20]。如图6(c)所示为MPU6050电路图。

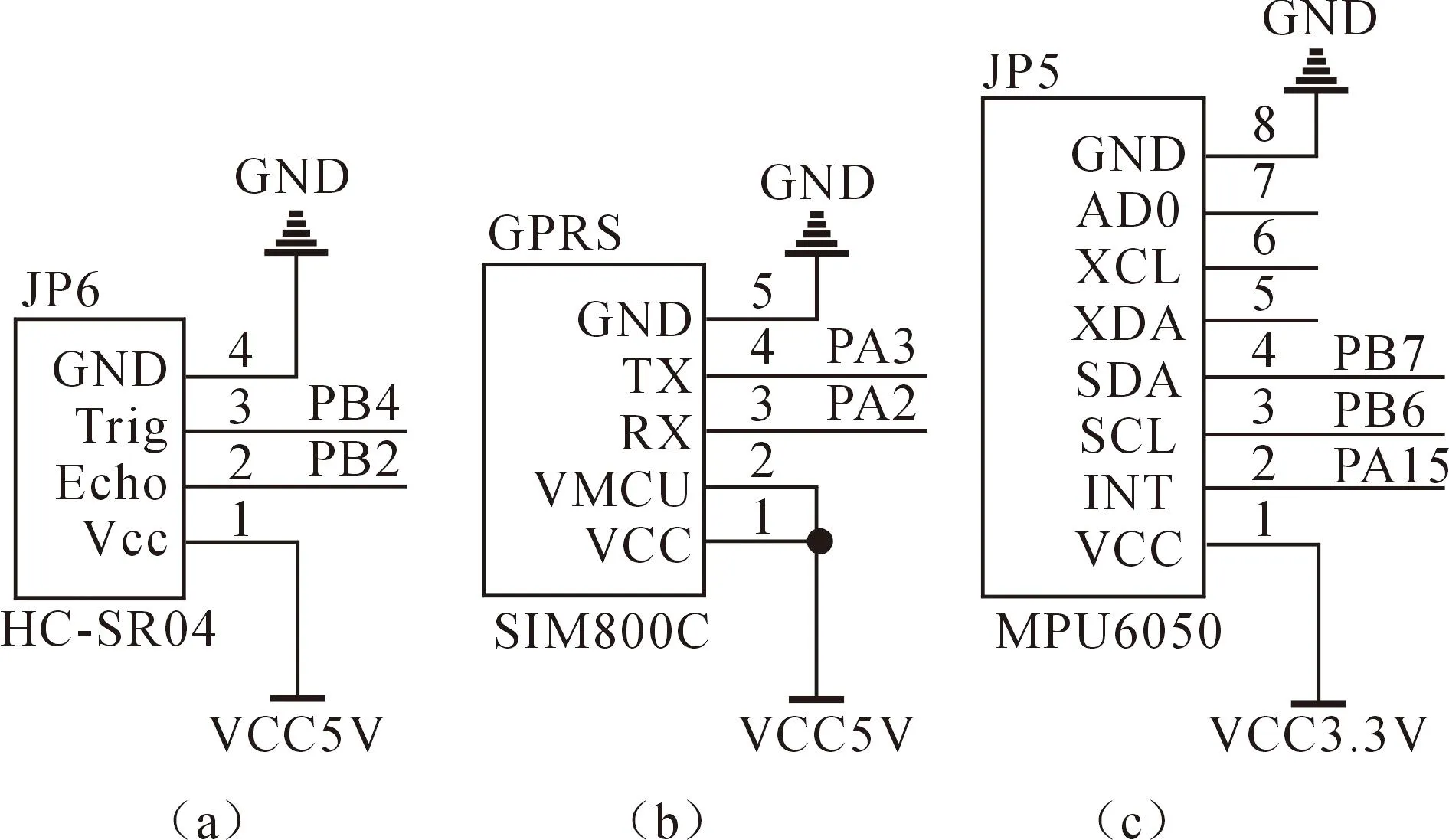
图6 传感器与主控的连接

3) 数据传输:以MQTT协议利用SIM800C上传边缘计算终端采集的数据,如图6(b)所示为SIM800C的电路图。边缘计算终端会将传感器采集到的水位和井盖姿态数据处理后以MQTT协议上传到云服务器中进行存储展示[21],存储起来以便后期查询使用。云平台一个页面可以添加多个图表,每个图表绑定对应的管网监测数据流后可以将数据以可视化图表动态显示出来,如图7所示为数据展示页面。

4) 双电源稳压电路部分:MCU和采集部分对电压的要求要低于GPRS部分,GPRS对电压的要求较高,当GPRS的电压小于正常工作电压时,无线通讯的信号会受到很大干扰,数据发送的丢包率会随着电源电压的降低而增大,因此采用双电源加稳压电路方法来作为系统的供电方式,以此来保证在监测节点的全生命周期内都能够稳定的监测管网数据。

4 实验测试及结果分析

为了测试本文提出的方法对管网的监测效果,分别采用本文提出的基于边缘计算和全生命周期的排水管网监测方法和传统的监测方法对某A地区部分管网进行监测,该地区平均海拔397 m,大气压95.92 kPa,最热均温度为35.5 ℃,在测试中记录了各项评价指标,对两种方法的测试结果进行对比分析,从而对本文监测方法的效果进行评估。

4.1 数据监测精度测试

4.1.1 水位监测

在水面平静和水面波动的情况下采用传统红外测距和本文的反射式超声波测距方式测量同一位置的水位到井盖的距离,通过与人工测量的实际数据对比,进而判断本文超声波测距方法的精度,如表2所示为不同场景、测试方式下测量数据的对比。

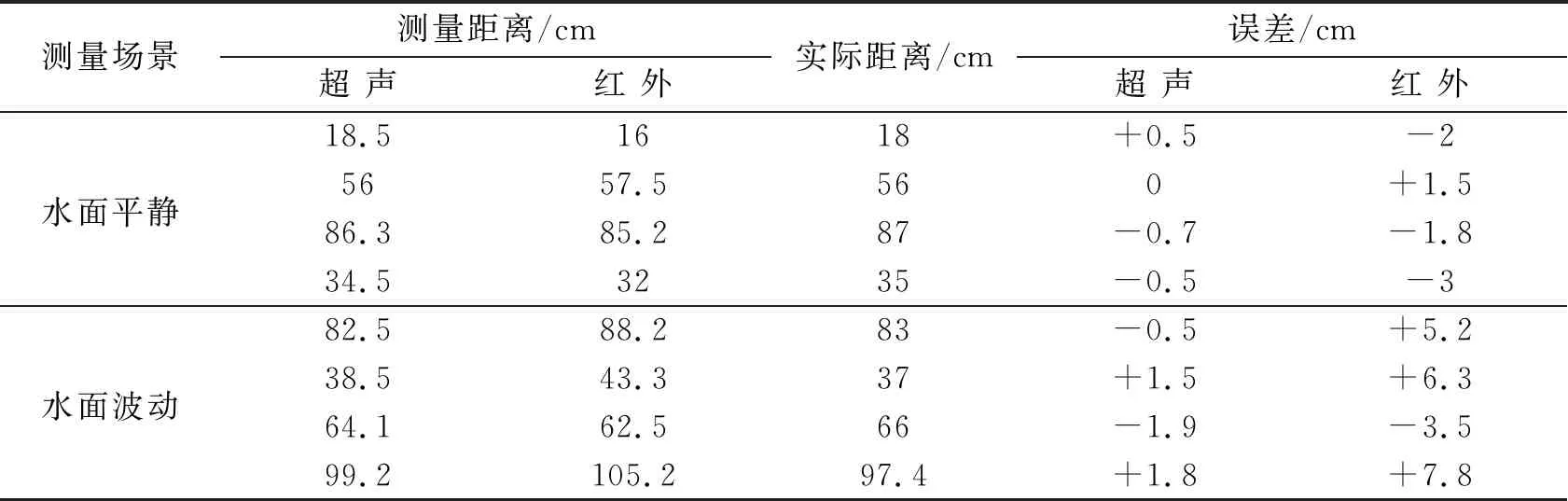
表2 水位监测精度对比

从表2中可知,在水面平静的情况下,本文方法测量的水位数据与实际测量的数据误差控制在1 cm以内,而红外测距的误差在1.5 cm以上;在水面波动的情况下,超声波测量数据误差在2 cm以内,红外测距在水面波动的情况下误差更大,在3.5 cm以上。可以说明本文采用的反射式超声波测距误差补偿模型更适合在井下环境工作,干扰较小,测量稳定。

4.1.2 井盖姿态监测

分别选择不同的方向以不同的角度倾斜管网井盖,同时观察监测数据曲线是否发生变化,以及灵敏程度,以此来判断基于Manony滤波算法的管网井盖姿态解算模型对井盖姿态的测量精度,如表3所示为不同倾斜角度下MPU6050采集的数据,如图7所示为管网井盖欧拉角的变化曲线图。

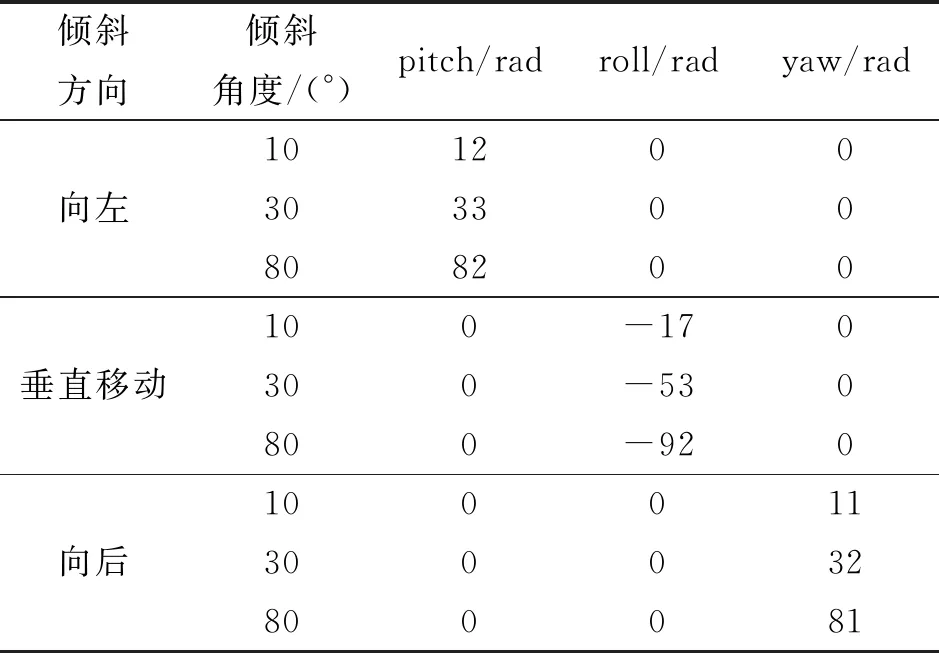
表3 管网井盖倾斜角度与三轴数据

测试结果表明,当管网井盖倾斜时,三轴姿态数据有非常明显的线性变化,能够很清楚的反映管网井盖姿态变化,并且经过边缘计算进行误差补偿后,三轴的精度进一步的提高,极大的提高了姿态监测灵敏度;同时如图8表明,在管网井盖姿态发生变化时,陀螺仪采集的数据曲线会发生突变,可见本文采用的基于Manony滤波算法的管网井盖姿态解算模型能够精确的反映井盖姿态变化。

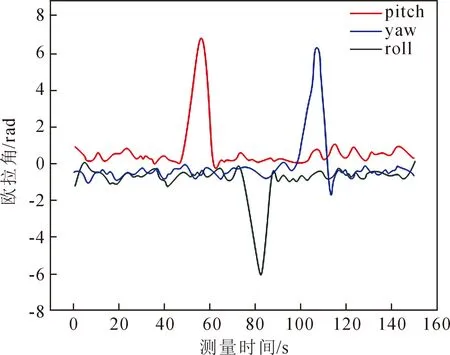
图8 管网井盖欧拉角变化

4.2 全生命周期监测稳定性测试

分别选择传统单电源供电和本文提出的的双电源稳压供电的监测节点,同时为了模拟监测节点全生命周期下的电压变化情况,需要先测量监测节点各模块在工作和低功耗状态下的平均电流,监测节点全生命周期不同时间节点的电源剩余容量为

(14)

文中采用18 650电池,水温为10 ℃、充放电次数为0～200次的电压与放电电量的估算模型[22],计算出对应的衰减电压,从而模拟监测节点在18个月的生命周期内随着使用时间增加导致电源电压发生衰减的情况,统计同一工作时间下两种监测节点发送数据量和云服务器收到的数据量,计算丢包率,以此来判断监测节点全生命周期的监测稳定性,如表4为丢包率对比。

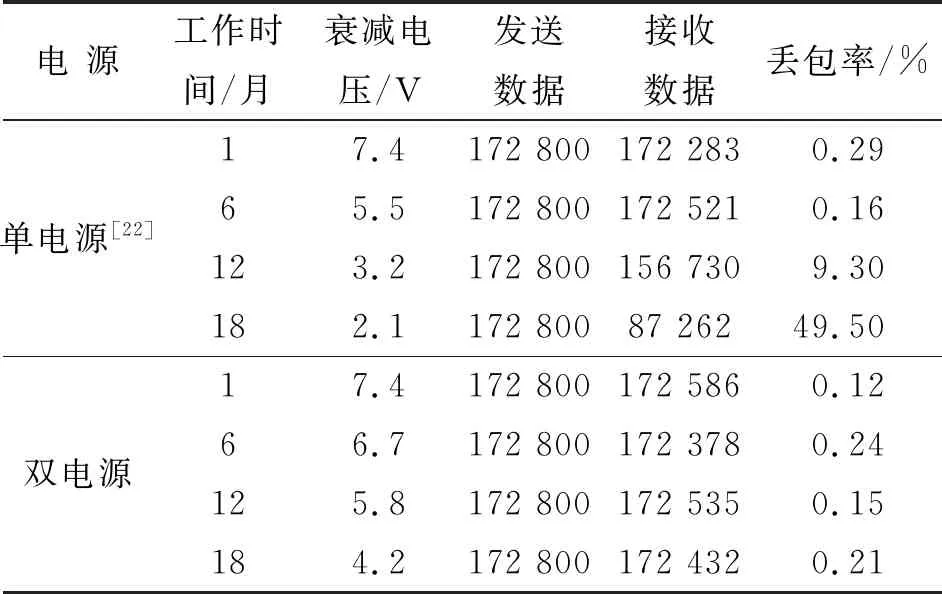
表4 丢包率测试

从表4可知,传统的单电源监测节点随着工作时间的增加,电压很快会降到3.3 V以下,而随着电压的下降,丢包率也会明显增大。在生命周期后期,当电压低于3.3 V时,丢包率快速增加,监测非常不稳定;而采用本文双电源稳压电路的监测节点全生命周期保持稳定的电压输入,抗干扰性较强,丢包率趋于稳定,在长期的使用下电压干扰较小,丢包率能维持在0.33%以下,可以说明该方法能够有效的解决监测节点全生命周期内电压衰减对监测稳定性的影响,延长系统使用时间。

5 结 论

1) 本文提出了一种基于边缘计算和全生命周期的排水管网监测方法,构建了反射式超声测距误差补偿模型与基于Manony滤波算法的管网井盖姿态解算模型,相较于传统的管网监测方法,本文提出的方法通过对超声波与陀螺仪的误差进行分析补偿,能够有效的提高测量精度,并降低海拔对管网监测的影响;同时引入了边缘计算,不仅能够极大的降低管网监测的数据量,还增加了边缘计算终端的续航时间,从而减轻后期数据处理压力实现对管网的全生命周期长期稳定的监测。

2) 文中方法在全生命周期内,能够精确测量管网水位和井盖姿态并进行异常告警,数据丢包率维持在0.33%以下,水位测量精度小于2 cm,系统运行非常稳定,并且具有良好的鲁棒性。为智慧城市建设以及智慧管网监测体系的构建提供了技术支撑,这将有广阔的应用前景,会使城市排水管网监测迈入一个智能化的时代。