配电网与电动汽车光储充电聚合商的协调互动策略

李耐心，文艺林，杜 鹏，杨宁辉，胡泽春

（1.国网冀北电力有限公司唐山供电公司，河北唐山 063000；2.清华大学电机工程与应用电子技术系，北京 100084）

0 引言

近年来，电动汽车[1]（Electric Vehicle，EV）、小型光伏发电[2]（Photovoltaic，PV）和储能系统[3]（Energy Storage Systems，ESS）在世界各国持续发展，已经成为智能电网和微电网框架的重要组成部分[4-6]。这些资源的接入改变了负荷侧的能源结构[7-8]。站在电网运营商的角度，将负荷侧可控资源纳入电网调度决策中，可提升电网运行的安全性和经济性[9-10]。站在可控资源的角度，利用其功率灵活性为电网提供可调能力可获得一定的经济补贴，最大化其使用价值[11-12]。

针对电动汽车、分布式发电和储能参与配电网调度，国内外学者已经开展了大量的研究。文献[13-16]构建了大量可调资源聚合后的可调能力等效模型，但并没有讨论如何利用该模型进行决策以及误差校验的方法。文献[17]考虑电动汽车有序充电提供的调节能力，以最小化网损为目标建立配电网最优潮流模型，只计及了电动汽车集群，没有细化到每辆电动汽车。文献[18]将电动汽车有序充电分为配电网指令生成、站内实施调控两阶段进行优化，但是配电网的潮流被简化为功率平衡的形式。文献[19-21]均采用分布式优化算法求解配电网最优潮流与电动汽车有序充电的联合优化问题，具有通信成本低和有效保护隐私的特点，但其中站内的调度问题都简化为聚合体的形式，没有考虑调度指令的进一步分解。

针对现有研究中的局限性，本文提出了一种配电网与电动汽车光储充电聚合商的联合运行优化策略。EV，PV 及ESS 由聚合商聚合为统一形式后参与配电网最优潮流的计算，得到对聚合商的调度指令，聚合商根据自身的利益计算出对该指令的反馈，配电网运营商需要在最优潮流计算中考虑该反馈。迭代收敛到一致的功率曲线后，在聚合商内部进行校验和再分配，将指令分配到每个资源上；本文设计了配电网与聚合商之间的信息交互机制，基于分析目标级联算法进行迭代求解，算法收敛的结果保证了配电网和聚合商双方的利益。在此基础上，提出了聚合商内部的校验和调度模型，得到每个资源的运行策略。

1 电动汽车光储充电聚合商可控模型

1.1 电动汽车光储充电聚合商能量流建模

电动汽车光储充电聚合商控制电动汽车、光伏发电系统及储能系统，三者之间可进行能量传输，也可与电网之间进行能量的交互。不同单元之间的能量流动关系如图1 所示。其中，S 表示储能系统，G 表示电网，X2Y表示功率从X流向Y，X和Y可取PV，EV，S 和G。

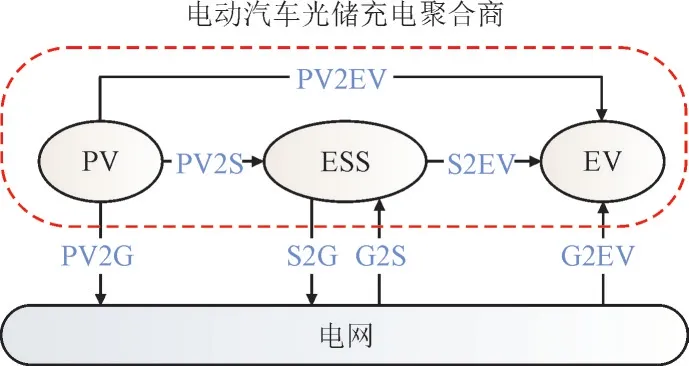
图1 电动汽车光储充电聚合商能量传输图Fig.1 Diagram showing energy transmission of aggregators of PV，ESS and EV

光伏发电系统所发出的电力可通过储能储存，或用于电动汽车充电，或直接卖给电网，其能量只能流出。储能系统接收光伏和电网的电力，可给电动汽车充电、向电网售电，其能量既可输出也可流入。电动汽车充电的能量来源可以是光伏系统、储能，也可直接从电网中获得，其能量只能流入。这些能量流动关系直接写成公式形式比较繁琐，因此使用“节点-支路关联矩阵”统一描述，加引号是因为它与图论中的节点支路关联矩阵不同。具体而言，将图1 所示的系统中光伏、储能、电动汽车和电网视为4 个节点，定义节点功率净流出矢量Pn与支路功率流矢量Pb如下：

式中：上标G，PV，S 和EV 分别为电网、光伏、储能和电动汽车。

定义节点-支路关联矩阵A如下：

由此，图1 中的系统能量流动关系可表示为：

式（4）包含了图1 中展示的聚合商中各个资源之间的能量流动关系，式（5）表示各个功率流动路径中流动的功率均为正。

1.2 可控资源聚合模型

聚合商位于配电网上的一个节点，该节点类型为PQ节点，其有功功率P具有调节能力。在最优潮流中，不考虑该节点内部的能量流动，而是将该节点的所有可控设备聚合为一体进行上报，不仅提高了计算效率，更重要的是保护了聚合商和用户的隐私。使用文献[22]提出的灵活资源模型，灵活资源在时段t消耗的功率需要满足功率和能量上下界约束，即：

对于不同类型的资源，其功率与能量上下界的生成方式不同。对于光伏发电，其功率上界为0，功率下界为其最大发电功率，能量上界为0，能量下界为从第1 个时段到第t个时段发出的全部电量。对于储能，其功率上下界分别为其充电和放电功率，能量上下界则分别对应电量充满和电量耗尽。需要注意的是，储能的荷电状态需要在规定时间内平衡，因此要求在最后一个时刻将能量恢复到初始水平。对于电动汽车而言，不考虑放电的情形，则其功率上界为最大充电功率，功率下界为0，能量上下界分别为其最快和最慢的充电能量变化曲线。生成不同资源的聚合模型后，将功率与能量边界参数叠加即得到聚合商整体的功率与能量边界，具体的建模形式与推导参见文献[23]，本文不再赘述。

在配电网的最优潮流计算中，仅需要聚合商整体的功率与能量边界信息。在用于生成迭代反馈的聚合商内部优化问题中，则需要考虑内部各个资源的能量流，此时无需考虑对每辆电动汽车分配功率，仍然使用聚合模型（6）对电动汽车进行聚合，收敛后的校验和再分配计算中才需计及每辆电动汽车的充电过程。

2 基于分析目标级联的配电网与聚合商联合优化策略

设聚合商的编号为l，所有聚合商的集合为L，聚合商的个数为L，则配电网与聚合商各自求解的问题及它们之间的信息交互机制如图2 所示。

图2 配电网与聚合商的模型与信息交互机制示意图Fig.2 Mechanism of model and information exchange between distribution network and aggregators

2.1 计及聚合商反馈的配电网最优潮流模型

本文最优潮流模型以最小化全时间段的总网损为目标，目标函数FDS如下：

式中：T 为优化所考虑的所有时间段的集合，Re（·）为取实部的运算符；s0,t为平衡节点在第t时段的复功率。

考虑辐射状配电网，使用DistFlow[23]表示潮流方程，则网络约束为：

∀t∈T ：

式中：i，j，h为节点编号；N+为去掉平衡节点的节点集合；（i，j）为从节点i到节点j的支路；A为支路的集合；h∈i为节点h与节点i相连；si,t为节点i在第t时段的复功率；Sij，t，Shi，t，Sh0，t分别为时段t从节点i流向节点j、从节点h流向节点i、从节点h流向根节点的复功率；zij，zhi，zh0分别为支路（i，j），（h，i）和（h，0）的阻抗；为zij复共轭；Iij，t为支路（i，j）上电流幅值的平方；vi，t，vj，t分别为时段t节点i和j电压幅值的平方；为节点电压平方的下限和上限。

式（8）—式（11）与传统的交流潮流方程在物理上完全等效，只是所使用的物理量不同，而式（12）是节点电压的上下限约束。式（11）是非线性等式约束，导致最优潮流问题非凸，因此对其进行二阶锥松弛[24]，转化为式（13）的形式。当配电网中没有反向功率流或反向功率流不大，且电压约束不起作用时，该松弛是精确的[25]。

配电网中的节点还需满足本地约束，对于固定负荷节点，本地约束即为功率注入值约束：

而可控节点的本地约束有所不同，除了式表示的功率和能量上下界之外，还需满足配电变压器的容量约束。假设可控资源聚合商都安装了无功调节设备，保证其对外无功净流量为0，则聚合商所在的配电网节点处本地约束包括：

式中：Pl,t为分配给聚合商l的总有功负荷；设聚合商l位于节点i，Ci为该节点的变压器容量。

式（15）为聚合商l的功率能量边界约束，式（16）计算出节点i的复功率，而式（17）表示配变容量约束。

求解最优潮流问题式（8）—式（10）、式（12）—式（18）可得到每个聚合商的有功功率该有功功率由配网运营商作为指令发送至聚合商l。聚合商通过计算其内部优化问题生成对该指令的反馈信息，即影子价格λl,t。配电网运营商在最优潮流计算中需考虑此反馈信息，则将目标函数改为增广拉格朗日函数F′DS：

式（8）—式（10）、式（12）—式（18）所给出的最优潮流模型是目标函数为二次函数的二阶锥规划问题，因此是凸规划问题，满足分析目标级联的收敛条件。

2.2 可控负荷资源聚合商的反馈模型

目标函数式（19）表示最大化聚合商的净利润，式中等号右边第一项求和表示从电网取电的成本，第二项求和表示向电网反送电所获的收益，第三项求和表示聚合商为电动汽车充电所赚取的利益，注意第三项求和前面系数为正，这是因为表示的是电动汽车向外流出的功率，为负值，最后一项是为避免多解而使用的l2正则化项。

约束条件首先包含第1 节所介绍的聚合商能量流模型式（1）—式（5）；式（20）表示聚合商对外满足配电网的指令，通过该式生成反馈信号；式（21）和式（22）是电动汽车聚合模型的功率与能量边界；式（23）和式（24）中表征了光伏发电的调节能力；式（25）和式（26）中给出了储能设备的功率调节能力；式（27）表示储能的能量平衡约束，保证结束时储能的荷电状态恢复到初始状态；式（28）约束了储能的能量变化范围。

聚合商的优化模型式（19）—式（28）为二次规划模型，由于电动汽车仍然是聚合模型，并且多个可控资源聚合节点可并行计算该内部优化模型，生成的反馈信息直接发回配电网，不仅提高了计算效率，还有效保护了各主体的隐私。

考虑聚合商反馈的配电网最优潮流模型式（8）—式（10）、式（12）—式（18）和考虑配电网指令的聚合商内部优化模型式（19）—式（28）之间交替迭代，从而收敛到一致的最优解。收敛后得到的最优解意味着配电网网损成本和各个聚合商总运行成本之和最低，符合配电网运营商和各聚合商的利益。

2.3 聚合商内部校验与再分配策略

迭代结束后，聚合商根据收敛的功率曲线结果将功率分配到每一个可控资源上。在此前的聚合商的优化模型式（19）—式（28）中，站内所有的电动汽车是聚合后作为一个整体来考虑的。当聚合商与配网运营商协同达到收敛后，需要将收敛后的聚合商总功率曲线具体分配为每个资源的功率曲线。由于聚合后的功率曲线不一定满足每辆电动汽车的充电约束，因此需要先校验再进行分配。

校验模型的目标是最小化实际功率曲线与指令曲线的偏差，需要在3.2 节模型基础上将目标函数改为式（29）的形式，同时去掉式（20）约束条件。而为了将功率分配到每辆电动汽车，需要去掉式（21）和式（22）约束条件，新增式（30）—式（32）约束条件。

式中：xm,t为电动汽车m在时段t的充电功率（标幺值，基值为额定功率）；am,t为电动汽车m在时段t的状态，其值为1 表示接入充电桩，0 表示未接入或已离开；M为所有电动汽车的集合；分别为电动汽车m到达时，离开时和最大的荷电状态（标幺值，基值为电池最大容量Bm）；Pchg为额定充电功率；ηEV为电池充电效率。

目标函数式（29）表示最小化指令功率曲线和实际可分配的功率曲线之间的偏差。约束条件式（30）表示电动汽车只能在接入充电桩时充电，并且充电功率在0 到额定功率之间可调；式（31）表示需要在电动汽车离开前满足其电量需求，但不能超过其电池最大容量；式（32）计算了所有电动汽车的聚合的总功率。

根据修正后的模型式（23）—式（32）即可计算出最大程度满足调度指令的聚合商内部所有资源的功率分配方式，计算得到的目标函数最优值若为0，则表示指令功率可以完全分配至聚合商内每个资源上执行。若计算得到的目标函数最优值大于0，存在不能完全分配的情形，此时最优解中的表示使得分配误差最小的聚合商总功率曲线，记为。将作为新的指令，进入下一步再分配的计算。

再分配计算中仍然遵循经济效益最大化的原则，由于此时的指令曲线已经经过校验，所以再分配的模型中又恢复了关于指令的等式约束，由式给出。聚合商内部指令再分配的优化模型为式（1）—式（5）、式（19）、式（23）—式（28）、式（30）—式（33）。

本节给出的校验模型与再分配模型均为二次规划模型，由于电动汽车的数量较多导致变量较多，而校验模型与再分配模型都需求解1 次，不在迭代的过程中，因此整个计算过程效率较高。

3 算例分析

3.1 系统设置

本文算例仿真中使用IEEE33 节点配电系统，系统拓扑如图3 所示。

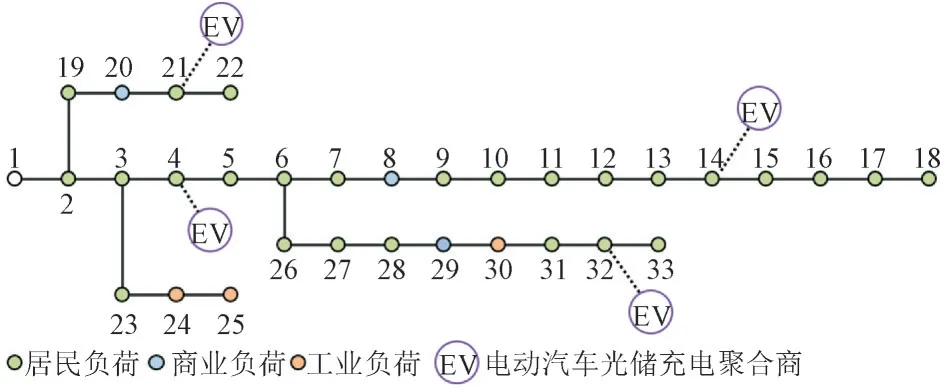
图3 IEEE33节点算例系统拓扑Fig.3 IEEE 33-node test case system topology

图3 中负荷节点包含居民负荷、商业负荷、工业负荷3 种，不同类型的典型日负荷曲线形状不同；节点4，14，21 和32 处接有电动汽车光储充电聚合商，每个聚合商包含的可控资源参数与规模如表1 所示；使用蒙特卡洛模拟生成每辆电动汽车的充电需求，零售电价和向电网反送电的电价均采用峰谷平3 段分时电价，电动汽车充电的服务费为恒定值，具体参数值见文献[22]。

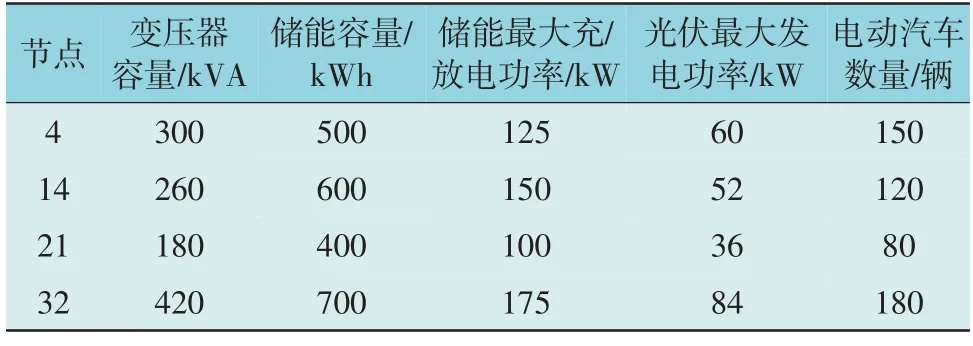
表1 聚合商可控资源规模Table 1 Scales of aggregators’controllable resources

3.2 仿真结果

3.2.1 收敛过程

迭代中网损计算结果与误差变化情况如图4所示，初始网损是对配电网运营商而言的最优值，经过协调之后配电网运营商做出了一定的妥协，若设置误差小于1×10-3则视为收敛，程序将在第11 次迭代达到收敛，收敛前后网损的变化不大。

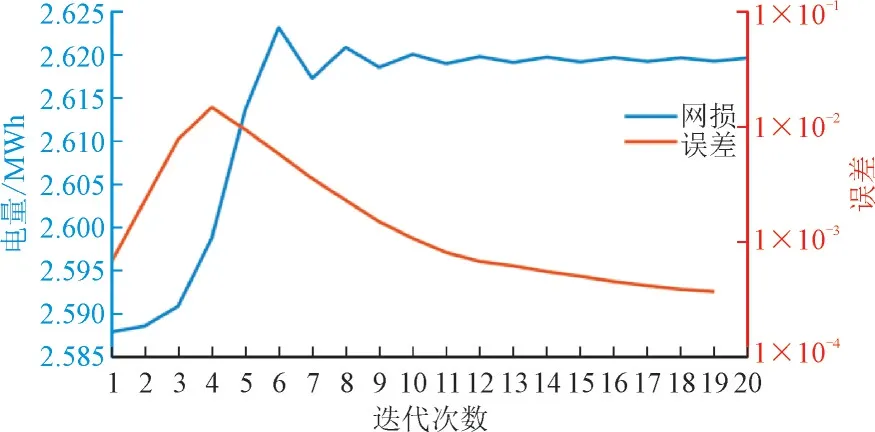
图4 迭代中网损与误差变化情况Fig.4 Changes in network loss and error during iteration

3.2.2 协调前后结果对比

图5 以位于配电网节点4 的聚合商为例，画出了初始指令功率曲线与协调一致功率曲线。

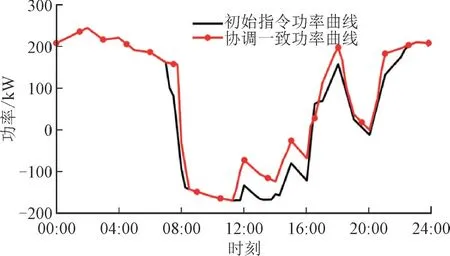
图5 迭代前后聚合商总体功率曲线对比Fig.5 Comparison of the overall power curves of aggregators before and after iteration

从图5 中可以看出，初始与收敛时的总体功率曲线也有不同程度的调整。表2 列出了协调前后所有聚合商净利润。由表2 可以看出，所有聚合商的净利润在协调后大大提高，这是因为计算初始指令的模型仅考虑了配电网网损却没有考虑到聚合商的利益。结合图4 中展示的配电网网损变化情况分析可知，经过本文的协调算法迭代后，在配电网网损变化不大的情况下显著提高了聚合商的收益，说明本文的协调算法很好地平衡了聚合商和配电网运营商的利益。

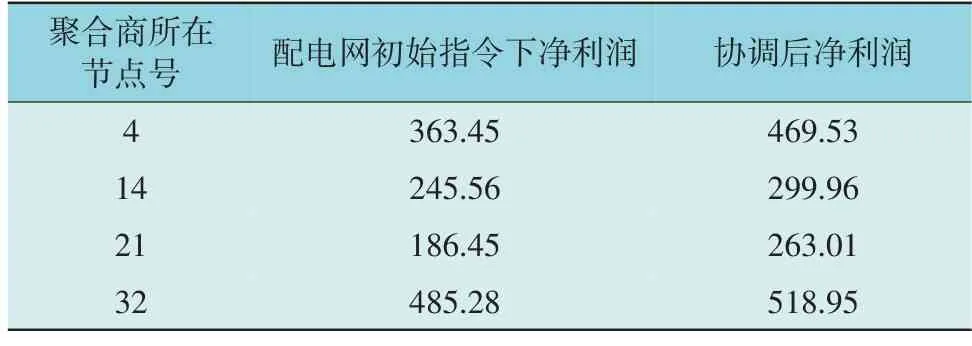
表2 协调前后聚合商净利润对比Table 2 Comparison of net profit between aggregators before and after coordination（元·d-1）

3.2.3 聚合商功率对指令的再分配结果

图6 展示了位于配电网节点4 的聚合商利用其所控制的资源对指令曲线进行再分配的结果，其中PG表示总体功率，PPV表示光伏发电的功率，PS表示储能充放电功率，PEV表示电动汽车总充电功率。从图6 中可以看出迭代收敛一致的功率曲线均通过了校验，各个聚合商都在利用其可控资源的容量进行调节，其共同特点是光伏发电均能完全利用，这也与聚合商的利益相符。

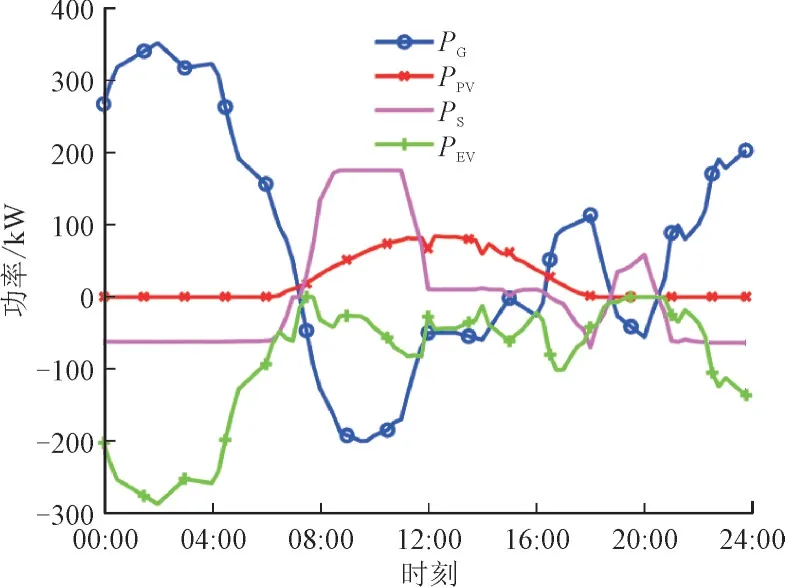
图6 功率再分配结果Fig.6 Result of power redistribution

4 结论

本文提出了配电网与电动汽车光储充电聚合商的协调策略。该协调策略能够充分考虑两者的利益，协调策略中的信息传递机制能够有效保护双方的隐私，并且使得配网运营商与聚合商的协调优化问题简化和分解，大大提高了求解的计算效率。在配网侧，使用二阶锥松弛后的Distflow 模型描述配电网侧最优潮流问题；在聚合商侧，使用简化的模型进行与配网运营商的交互迭代计算。配网运营商和聚合商通过有限的信息交换进行迭代计算，收敛后再将此时的功率曲线进行校验，并再分配到每一个可控资源。算例结果表明迭代过程中配电网的网损变化较小，但协调前后聚合商的净利润显著增加，验证了所提协调机制的有效性。协调后的功率曲线经过校验和再分配成功匹配到了聚合商控制的每个可控资源，该分配结果符合聚合商的利益。