考虑风光出力相关性与条件风险价值的孤岛型微电网经济调度

陈付雷，方毛林，汪辰晨，李金孟

（1.国网安徽经济技术研究院，安徽合肥 230000；2.中国能源建设集团安徽省电力设计院有限公司，安徽 合肥 230601；3.华北电力大学经济与管理学院，北京 102206）

0 引言

随着能源稀缺、环境污染等问题的日益严重，世界各国进行了能源结构变革，风、光等可再生能源得到了大规模发展[1]。由分布式能源构成的微电网系统依靠其经济成本低、环境友好、灵活性强等优势得到了广泛应用[2]。为了利用丰富的可再生能源满足远离主电网的岛屿、山区和其他偏远地区用户的用电需求，学者对微电网的孤岛运行模式进行了研究和应用[3]。然而，可再生电源的出力存在不确定性，在缺乏主电网的支撑时，可导致微电网供需两侧功率不均衡和输电线电压波动，严重影响了系统的安全稳定运行[4-5]。基于此，考虑可再生能源出力的不确定性对孤岛微电网调度运行进行优化是一个值得深入研究的问题。

目前，处理计及不确定性的微电网优化调度问题的主要方法为鲁棒优化方法。文献[6]提出了日前计划与日内调度的孤岛型微电网鲁棒优化算法。文献[7-8]提出了具有不同鲁棒调节参数的微电网自适应鲁棒优化调度模型，以提高大规模可再生分布式能源并入微电网系统的运行经济性和安全性。文献[9]建立了两阶段鲁棒优化模型，以找到微电网运行的经济性和稳定性之间的平衡点。然而，采用鲁棒优化方法确定最坏边界存在一定的主观性，并且随着智能算法、大数据技术的发展，微电网系统中的不确定性参数都会在预测情景附近波动[10]。

为此，基于场景生成的规划方法被应用于不确定参数建模，不确定性被模拟成一系列合理的离散场景，并且通过随机优化方法对场景进行求解，其优化结果与实际值非常接近[11]。文献[12-13]运用蒙特卡洛场景生成方法模拟可再生能源机组出力的不确定性，构建了微电网经济调度优化模型。在以往的研究中一般根据先验统计假设构建分布函数，导致拟合效果往往与真实情况相差较大[14]。另外，在微电网调度中，同一地区的风能和太阳能表现出了很强的相关性[15]，需要进一步深入研究。

此外，文献[11-13]缺少了可再生能源出力不确定性对目标函数影响的描述。为了评估参数不确定性对目标函数造成的风险损失，条件风险价值（Conditional Value at Risk，CVaR）理论在电力系统经济调度领域得到了很好的应用[16]。文献[17]考虑能源价格不确定性给电力系统调度运行带来的风险，采用CVaR 作为风险度量，建立了风险损失评估模型。文献[18]对风电、光伏出力的不确定性进行分析，在目标函数中引入CVaR 成本，对含可再生能源发电机组的虚拟电厂进行调度优化。在已有研究中，运用CVaR 对可再生能源出力不确定性造成的风险损失进行度量时，未对碳交易成本进行考虑。已有研究表明碳交易机制在提升微电网系统经济效益方面作用显著[19-20]。因此，本文在调度模型中引入碳交易机制，分析市场手段对降低系统运行成本和风险损失的作用。

综上，本文考虑风光出力的不确定性和相关性、风险损失及碳交易等因素对孤岛型微电网调度优化问题进行了研究。基于非参数核密度估计方法和Copula 函数构建风光出力联合概率分布模型，并通过蒙特卡洛模拟与K-means 聚类技术得到风光出力典型场景；运用CVaR 理论评估风光出力不确定性对系统造成的风险损失，构建了冷、热、电多能耦合的孤岛型微电网调度优化模型；分析碳交易机制对调度运行成本和风险损失的影响，利用可再生能源机组发电的优势，通过市场交易提升经济性。

1 风险损失和风光出力相关性建模

1.1 基于CVaR的风险损失度量

CVaR 表示在一定置信度水平β下，风险损失大于风险价值（Value at Risk，VaR）的期望。对于给定的β∈(0,1)，其对应的VaR 和CVaR 求解表达式如下：

式中：ψ(x,α)为风险损失不大于辅助决策变量α的分布函数；x为决策变量；ξ为导致系统风险损失的随机变量；ρ(ξ)为ξ的概率密度函数；f(ξ,x)为风险损失函数；αβ(ξ)为风险度量的VaR 值；R为实数；φβ(ξ)为风险度量的CVaR 值。

由于αβ(ξ)的表达式难以直接给出，参考文献[17]对CVaR 进行近似求解：

考虑到实际应用中概率密度ρ(ξ)求解的复杂性，对其进行离散化处理，将式（2）转换成式（3）所示：

式中：N为场景总数；pk为场景k发生的概率。

式（3）中α的最优值为αβ(ξ)。

1.2 风光出力典型场景生成

Copula 函数可以描述随机变量相关性，利用各变量的边缘分布函数求出联合分布函数[21]。由于不同类型Copula 函数的模拟结果存在较大差异。本文基于Spearman 秩相关系数、Kendall 秩相关系数指标，选取孤岛型微电网系统1 个月的风电、光伏出力数据，分别用Normal-Copula，Frank-Copula，Clayton-Copula 函数拟合风光出力，并计算Empirical-Copula 函数的秩相关系数，结果如表1 所示。各函数的指标值与Empirical-Copula 函数越接近，拟合效果越好。

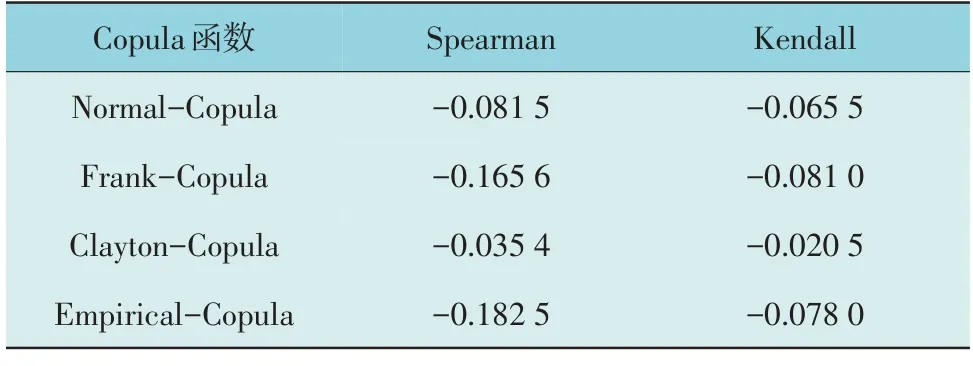
表1 Copula函数的秩相关系数Table 1 Rank correlation coefficient of copula function

由表1 可知，Frank-Copula 函数模拟的效果最佳，故而采用Frank-Copula 函数描述风光出力的联合分布函数。针对风光出力概率密度函数无法利用经验分布直接获取的问题，利用非参数核密度估计法建立概率密度函数。随后，运用蒙特卡洛抽样的方式进行场景生成，并基于K-means 方法进行聚类缩减得到风光出力典型场景。考虑累积分布函数的反函数求解难度较大的问题，利用三次样条插值法求解累积概率所对应的每个时段的采样风电和光伏出力。具体的典型场景生成步骤参考文献[15，22]。

2 计及CVaR 的孤岛型微电网系统多场景协同调度优化模型

本文构建了包含冷-热-电多能耦合的孤岛型微电网系统调度优化模型，系统结构如图1 所示。

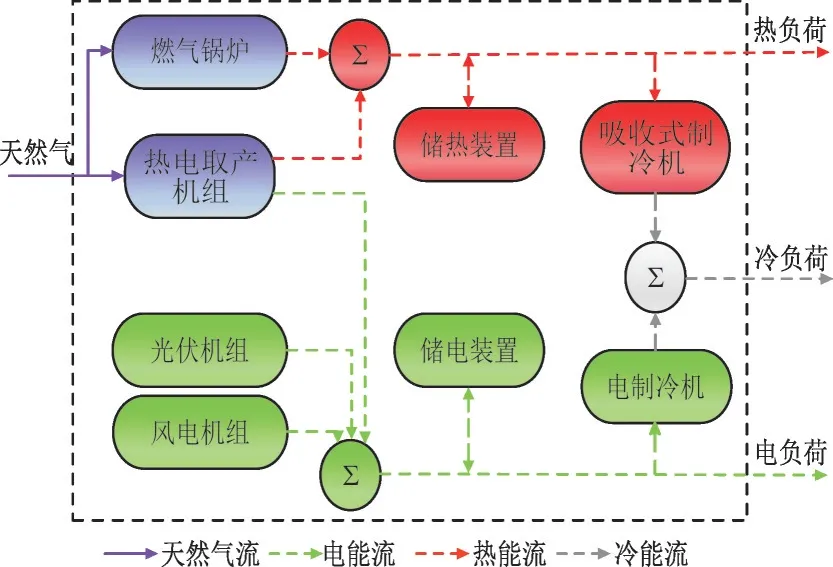
图1 孤岛型微电网多能耦合系统结构图Fig.1 Structure diagram of multi-energy coupling system of islanded microgrid

供能设备包括热电联产（Combined Heat and Power，CHP）机组、风电机组（Wind Power Plant，WPP）、光伏机组（Photovoltaic，PV）、燃气锅炉（Gas Boiler，GB）、吸收式制冷机（Absorption Chiller，AC）和电制冷机（Electrical Chiller，EC）；储能系统包括电储能（Electrical Storage，ES）和热储能（Thermal Storage，TS）；负荷类型包括电负荷、热负荷和冷负荷。

2.1 目标函数

优化目标设置为最小化系统日运行成本期望值的基础上，利用CVaR 进行风险规避。运行成本包括燃料成本Cfuel、运行维护成本Com、碳排放权交易成本Cct和环境污染惩罚成本Cenv。

2.1.1 系统运行成本

1）燃料成本为：

式中：t为调度时段，时间间隔为1 h，调度周期内共24 个时段；λgas为天然气单价；LHV为天然气的低热值；为CHP 机组的输出电功率，ηCHP,ele为CHP 机组的发电效率；为t时段燃气锅炉的输出功率，ηGB为燃气锅炉的能量转换效率。

2）运行维护成本为：

式中：λct为碳排放权交易单价；Et为t时段系统的CO2配额量，本文采取基准线法[23]确定该值；为t时段系统的CO2排放量；γ为系统碳配额系数，其值根据区域电网基准线排放因子确定；ϑCHP，ϑGB分别为CHP 机组和燃气锅炉的CO2排放强度。

4）环境污染惩罚成本为：

式中：I为污染气体类型总数；τi为第i类污染气体的排放惩罚系数；分别为CHP 机组和燃气锅炉的第i类污染气体排放强度。

系统中污染物类型包括NOx，SO2和CO2气体。

2.1.2 计及CVaR的调度优化目标函数

计及CVaR 的目标函数由2 部分组成：（1）多种场景运行成本的期望值；（2）CVaR 成本。通过引入风险偏好系数θ对CVaR 进行赋权，得到优化目标函数如式（8）所示。

一般认为θ值小于0.05 时为风险偏好，大于0.1 时为风险规避。

2.2 约束条件

1）能量转换约束为：

2）机组出力及爬坡约束为：

3）电储能单元约束为：

4）热储能单元约束为：

5）功率平衡约束为：

3 算例分析

3.1 系统参数与场景设置

为了验证已建模型的可行性和有效性，选取某一孤岛型微电网系统的数据作为算例进行分析。本文构建的调度优化模型为混合整数线性规划模型，利用GAMS/BARON 求解器进行求解。参考文献[21，24-25]给出系统运行的主要参数取值情况，如表2 所示；污染物排放参数如表3 所示；冷、热、电负荷曲线如图2 所示。根据历史数据，运用本文所提的典型场景生成方法生成5 个场景的风光出力曲线如图3 所示，其中采样规模设置为1 000 次。置信水平β=0.95，风险偏好系数θ=0.1。

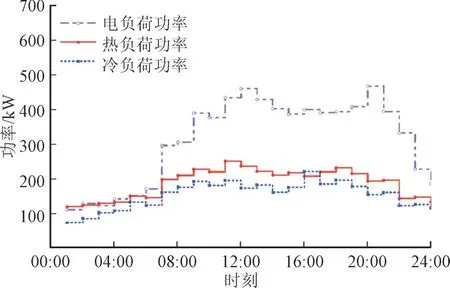
图2 微电网电、热、冷负荷曲线Fig.2 Curves for electric，thermal and cooling load of microgrid

图3 风光出力场景生成结果Fig.3 Results of scenario generation for WPP and PV output

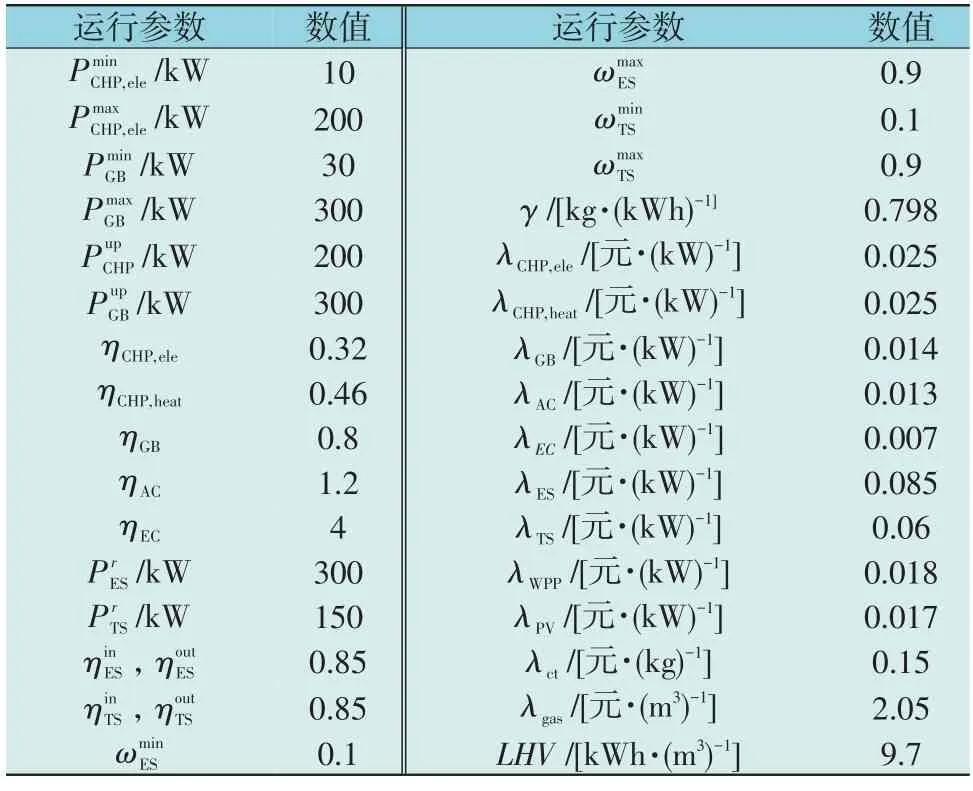
表2 系统运行参数Table 2 System operation parameters

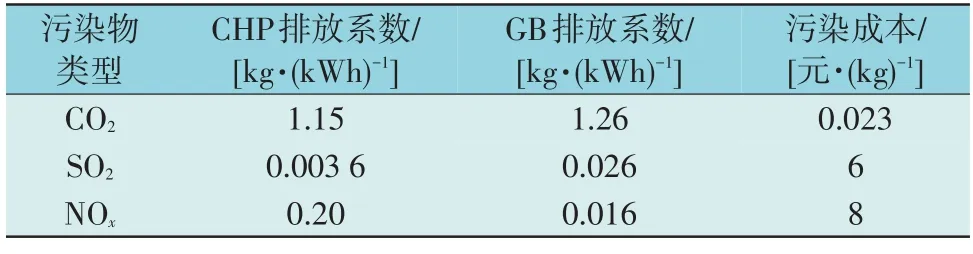
表3 污染物排放参数Table 3 Pollutant emission parameters

设置以下4 种情景进行对比分析：情景1，不考虑条件风险价值与碳交易机制进行调度优化；情景2，考虑条件风险价值，不考虑碳交易机制进行调度优化；情景3，不考虑条件风险价值，考虑碳交易机制进行调度优化；情景4，考虑条件风险价值与碳交易机制进行调度优化。

3.2 算例求解结果

3.2.1 能源供给结果

由于不同情景下系统通过调度满足冷、热、电用能需求的原理一致，并且不同风光出力场景只是数据值存在差异，不影响功率平衡机理，因此本节基于风光出力典型场景2，给出情景4 优化后的系统冷、热、电供能结果，其余情景不再赘述。

1）电负荷供给调度结果。图4 为电负荷的调度结果，图4 中在用电高峰时段（10∶00—20∶00），风电和光伏处于满负荷运行状态，未发生弃风弃光现象，系统通过CHP 机组和电储能设备放电满足其余的电量供应；在用电负荷需求低于电力供应时段（21∶00—5∶00），风电出力的多余电量被储存在电储能设备中，以满足高峰时期的用电需求；系统的弃风弃光总量为1 917.97 kWh。

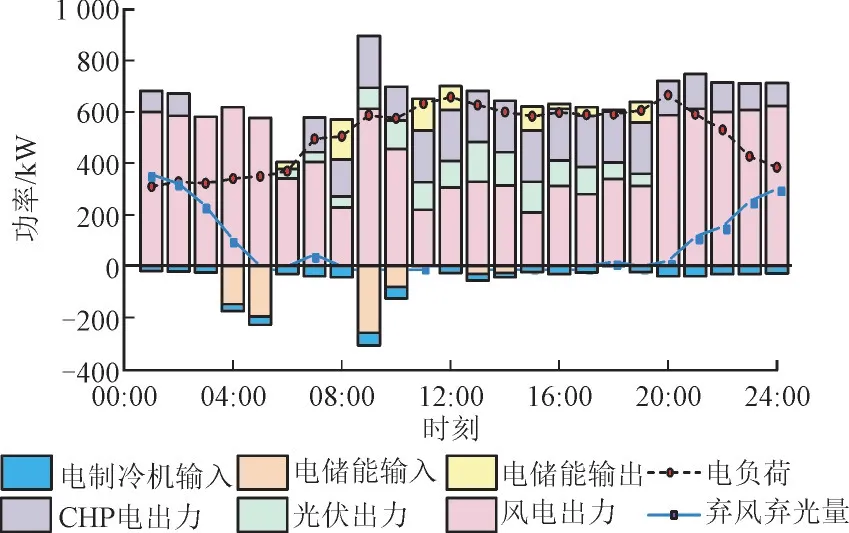
图4 电负荷的调度结果Fig.4 Scheduling result of power load

2）热负荷供给调度结果。图5 为热负荷的调度结果，图5 中在3∶00—6∶00，系统的热负荷由燃气锅炉提供，而在其他时段热负荷来自CHP 机组余热锅炉。结合图4 分析可知，3∶00—6∶00 电负荷需求较低，CHP 机组未出力，余热锅炉不提供热量；而在其他时间段CHP 机组处于运转状态，余热锅炉产生的热量基本满足系统用热需求。热储能装置在6∶00将多余的热量储存，并在18∶00 将热能放出。

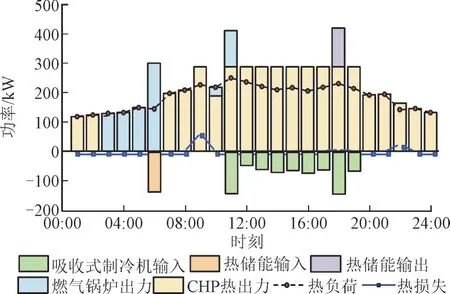
图5 热负荷的调度结果Fig.5 Scheduling result of heating load

3）冷负荷供给调度结果。图6 为冷负荷的调度结果，冷负荷由吸收式制冷机和电制冷机提供，二者协调运行以满足系统各时段的冷能需求。在11∶00—19∶00，冷负荷由吸收式制冷机提供，其余时段全部由电制冷机提供。11∶00—19∶00 电负荷需求较高，CHP 机组处于满负荷运行状态，余热锅炉产生的热量在满足用热负荷后，被输送到吸收式制冷机供给冷负荷；其余时段，电制冷机通过消纳可再生能源机组的发电量满足冷负荷。

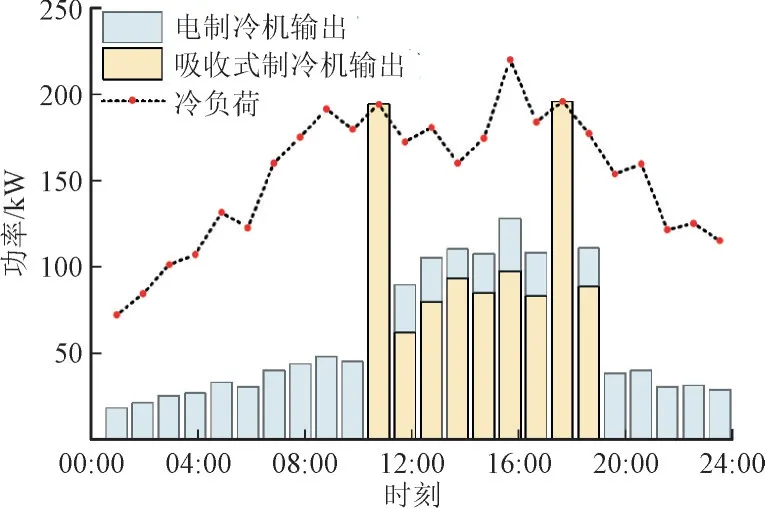
图6 冷负荷的调度结果Fig.6 Scheduling result of cooling load

3.2.2 调度优化结果

本文选取CHP 机组发电量、弃风弃光量、运行成本期望值和调度风险成本指标，对不同情景的调度优化结果进行对比，如表4 所示。

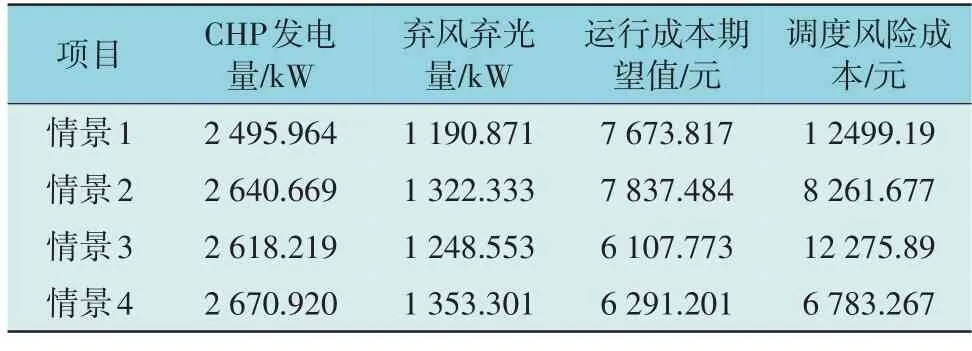
表4 不同情景的优化结果Table 4 Optimization results of different scenarios

3.3 调度结果分析

3.3.1 CVaR的合理性与优化效果分析

1）合理性分析：观察表4 可知，常规求解模型（情景1）求解时，微电网调度运行成本期望值为7 673.871 元，风险成本为12 499.19 元，按照式（10）求得的目标函数值为8 923.79 元。考虑CVaR 的调度模型（情景2）求解后，微电网调度运行成本期望值为7 837.484 元，风险成本为8 261.677 元，目标函数值为8 663.652 元。由此可知，考虑CVaR 后目标函数值降低了260.134 元，降低幅度约2.92%，体现了在目标函数中考虑CVaR 的合理性。

2）优化效果分析：以情景2 为例，考虑CVaR 进行经济调度时，相对于情景1，系统增加CHP 机组的发电量，减少风光机组的上网功率，以降低风光出力波动造成的风险损失。计算可知，系统用163.667 元的额外成本支出规避了4 237.523 元的风险损失；弃风弃光量增加了131.462 kWh，间接反映出系统应对风光出力波动的能力提升了131.462 kWh。因此，考虑CVaR 进行经济调度，可以帮助系统在计划制定阶段用较小的成本支出规避大额的风险损失。

3.3.2 碳交易机制效益分析

以情景4 为例，图7 展现了系统碳配额与碳排放情况。凭借可再生能源发电的优势，系统的碳排放量远低于配额值，富余的碳排放权额度为11 068.011 kg。按照碳交易价格0.15 元/kg 计算，微电网可获利1 660.20 元。

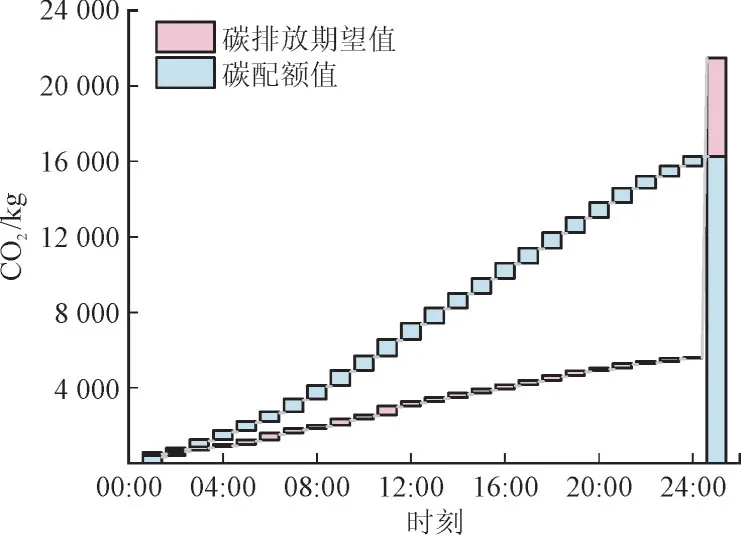
图7 调度周期内系统碳配额与碳排放情况Fig.7 Carbon quota and carbon emission of system in scheduling period

微电网作为以可再生能源作为主要电能输出的系统，在满足碳配额要求的情况下，碳排放权额度存在大量的富余，通过市场行为进行碳排放权交易、售出多余的额度，能够有效提高系统的经济性。

此外，对比情景3 与情景1 的调度结果，在碳交易机制影响下，系统运行成本期望值降低了1 566.044 元，降低幅度约20.40%，碳交易机制对微电网效益提升的作用显著。风险成本减少223.30元，减少幅度约1.79%，总体上看，风险成本虽有小幅度减少，但数值仍然很大。对比情景4 与情景2，系统运行成本期望值减少了1 546.283 元，减少幅度约19.73%，风险成本减少了1 478.41 元，减少幅度约17.89%。可见，碳交易机制不仅可以显著提升系统运行的经济性，而且可以有效降低系统的风险损失。

3.4 灵敏度分析

为了分析关键参数对优化结果的影响，选取风险偏好系数θ与碳交易价格λct，计算不同取值情况下调度优化的结果。

3.4.1 风险偏好系数对优化结果的影响

图8 为不同θ下的调度优化结果，θ的变化范围为0～0.15，间隔为0.015。由图8 可以看到，θ从0 增长到0.15，计及CVaR 的目标函数值从6 107.773 元增加到7 339.254 元。随着θ的增大，决策制定者越来越倾向于规避风光出力波动带来的风险，尽可能增加CHP 机组的发电量来满足用户负荷需求，导致更高的系统运行成本。此外，随着风光机组上网功率的减少，碳交易机制提升系统经济效益的作用也会降低。

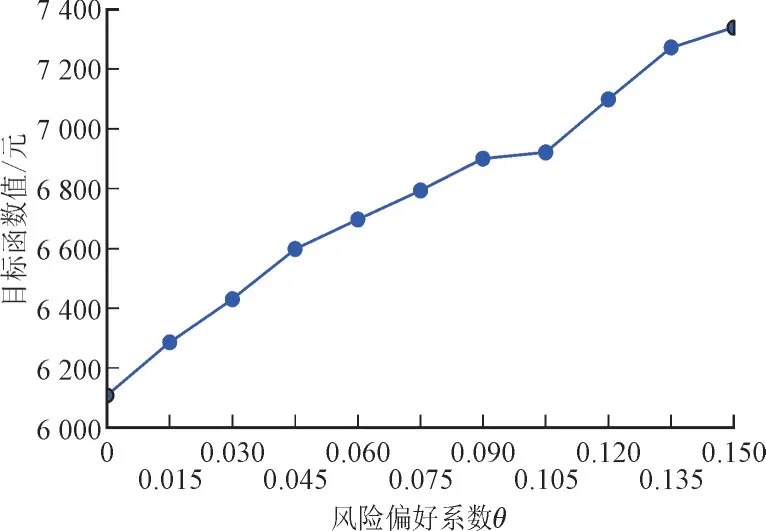
图8 不同θ 下的调度优化结果Fig.8 Scheduling optimization results with different θ

3.4.2 碳交易价格对优化结果的影响

图9 为θ=0.1 情况下，不同碳交易价格的调度优化结果，λct的变动范围为每吨100～200 元，间隔为10 元。由图9 可以看出，随着λct的增大，目标函数值由7 570.4 元减少到5 843.433 元。随着碳交易价格的增加，系统通过售出碳排放权获得的收益也会增加，降低调度运行成本的作用也会随之增强。

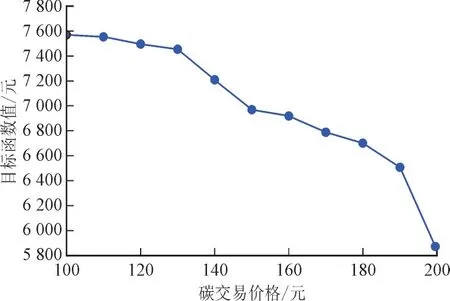
图9 不同碳交易价格下的调度优化结果Fig.9 Scheduling optimization results under different carbon trading price

4 结论

本文提出了一种综合考虑风光出力相关性与CVaR 的孤岛型微电网经济调度模型，计及机组发电、能量转换、碳排放配额、储能运行等约束。通过4 个场景的对比分析，验证了模型的有效性。主要结论如下：

1）计及CVaR 和运行成本对微电网进行经济调度，系统通过在计划阶段增加CHP 机组的发电量，减少风光机组的上网功率，实现了以较小的成本支出对大部分风险损失的规避。

2）碳交易机制的引入，有助于微电网系统充分发挥可再生能源发电的优势，通过市场途径提升运营效益、降低风险损失。

3）随着风险规避系数的增加，系统调度的目标函数值不断增大，反映了调度决策者对风险厌恶程度的升高；随着碳交易价格的变高，目标函数值不断降低，表明碳交易机制带来的经济提升和风险降低作用持续增强。

值得指出的是，本文只考虑了风光出力的不确定与相关性，并没有考虑风光出力与负荷的相关性，同时，碳交易价格也存在不确定性，如何在调度运行中考虑这些因素的影响是下一步深入研究的方向。