移相全桥直流变换器阻抗降阶建模及附加有源阻尼控制

李欢，姜文伟，陈鹏伟，李昊键

（1.直流输电技术全国重点实验室（南方电网科学研究院），广州 510663；2.南京航空航天大学，南京 211106）

0 引言

随着电力电子技术的快速发展及分布式新能源、直流负荷比例的增加，直流配电系统在灵活可控、配电容量和效率等方面的优势逐渐凸显，已成为未来电网乃至能源互联网的重要发展方向之一［1-3］。

国内外多家科研单位、高校和企业对直流配电系统的相关技术、实验系统和示范工程展开了持续研究［4-6］。然而，当换流站、负载变换器采用定功率或定输出电压控制时，在直流侧均表现为恒功率负载，其负阻特性易导致各子系统间出现交互问题，甚至在背景谐波作用下产生受迫振荡［7-9］，往往需配置一定的阻尼环节以保证系统稳定运行。

与无源阻尼相比，有源阻尼控制策略通常在控制环路中注入补偿信号来实现对电压电流的振荡抑制，在改善系统稳定性的同时避免了额外功率损耗，因而受到广泛关注。针对定直流电压控制的有源变换器，文献［10］采用直流母线电压反馈，提出了3种分别针对直流电压、d轴电流和d轴电压进行补偿的有源阻尼解决方案；文献［11］采用串、并联虚拟阻尼支路分别推导了直流电压反馈、直流电流前馈两类有源阻尼补偿环节；文献［12-13］则设计了扰动电流前馈和功率前馈的有源阻尼补偿环节，增强了电流内环对母线电压波动的跟踪能力；文献［14］针对DC/DC 源变换器采用电感电流反馈的有源阻尼方式增加虚拟阻尼支路，并指出虚拟支路的引入位置对系统不稳定极点的补偿效果存在较大差异。文献［15］提出一种计及低通滤波器的有源阻尼抑制方法，通过改变换流器的等效输出阻抗，使主导特征根向s域平面左移。文献［16］则通过附加虚拟电阻的下垂控制方式增强系统阻尼，提供系统稳定性。然而，当源侧变换器因黑盒限制或输出要求无法配置有源阻尼控制时［17］，若仍寻求输入/输出阻抗匹配以提高系统稳定性，负载变换器成为潜在的有源阻尼配置对象。

针对负载变换器，文献［18］以等效实现虚拟并联电阻为核心，设计了直流电压前馈的有源阻尼控制策略；文献［19-20］分别提出了适用于定功率站的交流电流反馈和直流电流前馈有源阻尼控制策略；文献［21］以直流侧电流为前馈，推导了定功率和定交流电压两种控制方式下的负载站有源阻尼补偿环节；文献［22］则提出了一种自适应输入阻抗调节方法，使虚拟阻抗与负载变换器输入阻抗并联以调节特定频段的负载负阻尼特性，控制器较为复杂。上述有源阻尼控制中，虽然反馈/前馈量覆盖面较广，且补偿环节形式、位置及对象也各有不同，但均局限于定功率或定交流电压控制下的负载站，面对其他控制模式下的负载站调节能力有限，使多源阻尼协调配置的需求逐步体现［23-25］。

为满足复杂系统中有源阻尼的多源配置需求，本文选取在高输入电压和中大功率场合得到广泛应用的移相全桥（phase-shifted full-bridge，PSFB）负载变换器作为主要研究对象，在建立其降阶小信号模型的基础上，采用并联虚拟阻尼支路的方式对输入电压前馈有源阻尼控制进行了溯源，并通过低频段阻抗换算提出了输出电压反馈有源阻尼控制策略，可等效实现PSFB 变换器输入端并联虚拟电阻进而强化系统阻尼的效果。最后，针对含PSFB 变换器的双端直流配电系统，通过时域仿真、小信号特征值轨迹对比和硬件在环实验，验证了PSFB 变换器阻抗降阶模型的准确性与有源阻尼策略的有效性。

1 PSFB变换器等效电路模型

1.1 开关模态分析

图1 展示了PSFB 变换器的基本电路结构，S1与S3 组成超前桥臂，S2 与S4 组成滞后桥臂；Di与DRi分别为源侧开关管反并联二极管与负载侧整流二极管（i=1，2，3，4），Cp、Lr、Lf与Cf分别为源侧电容、变压器T 的等效漏感、负载侧滤波电感与电容；up与uf为源测与负载侧电容电压；ir为变压器T 的原边输入电流，if和iL分别为负载侧滤波电感输入和输出电流，ip为桥臂输入电流；Pin和Pout分别为PSFB 变换器的输入和输出功率；K为变压器原副边匝数比。

图1 PSFB变换器电路结构Fig.1 Circuit structure of PSFB Converter

忽略开关损耗与结电容，PSFB 变换器工作波形可简化如图2 所示，D、Dloss和Deff分别为控制器实际输出占空比、丢失占空比和有效占空比，Ts为开关管开关周期。

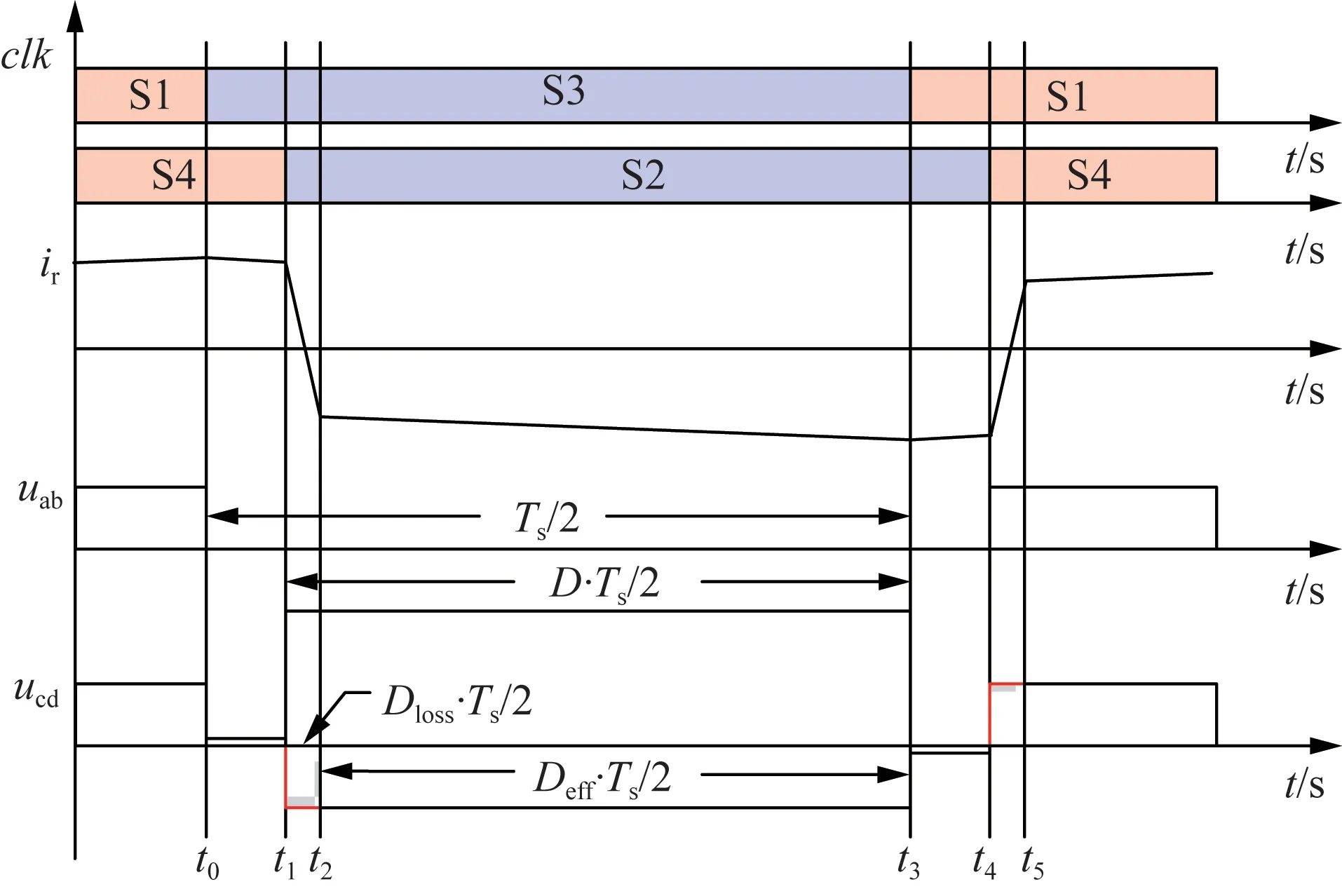
图2 PSFB变换器理论波形Fig.2 Theoretical waveforms of PSFB converter

若将半周期划分为开关模态1（t0—t1），开关模态2（t1—t2）和开关模态3（t2—t3），则t∈(t0，t1)时，S1 关断，D3 自然导通，变压器原边电流ir（t）和滤波电感电流if（t）满足式（1）—（2）如下。

类比可得含开关模态2和3的完整电流响应式，并给出关键参数Dloss和Deff的求解过程如式（3）所示。

式中含Δ符号的变量代表该变量的小扰动。

由if(t3)=if(t0)，可得：

式中deff和d分别为有效移相占空比和实际移相占空比。

通常Lr＜＜Lf，稳态下if(t1)近似为稳态值If，则式（3）可简化为Dloss=。

1.2 平均变量等效电路

为便于建立PSFB 变换器的状态空间模型，采用受控源来等效替代其中开关元件部分，构建PSFB 变换器平均变量等效电路。忽略开关管与变压器损耗，PSFB 输入功率Pin与输出功率Pout相等，如式（5）所示。

式中K(D)为占空比函数。

结合式（7）所示各开关模态下的uout、平均桥臂输出电压如式（8）所示。

假设up、uf在一个周期内的变化不大，可近似看做一个周期内二者恒定不变，可得：

若Lr＜＜Lf，可得变换器输入输出电压关系。

由功率平衡关系，可知PSFB 变换器输入输出电流关系满足ip=，PSFB 变换器平均变量等效电路如图3 所示，其中Rs和Ls为电源内阻和滤波电感；RL和LL为负载电阻和电感；ik为受控电流源，is为电源输出滤波电感电流。

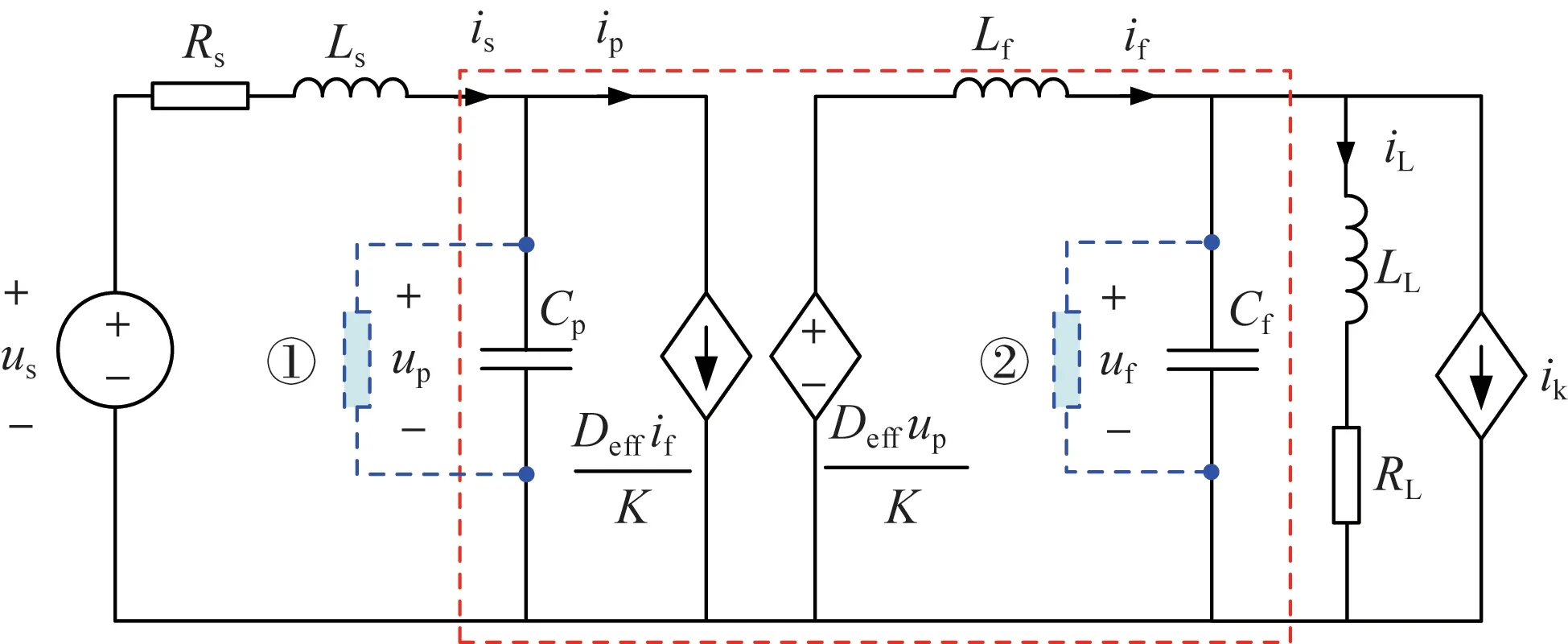
图3 PSFB变换器平均变量等效电路Fig.3 Average variable equivalent circuit of PSFB converter

2 PSFB变换器阻抗降阶模型

2.1 全阶小信号建模

PSFB 变换器的典型控制方式包括电压控制模式和电流控制模式二类。考虑输入电压响应与输入电压控制特性，以平均电流控制为例进行分析，其控制方程如式（11）所示。

式中：Kp、Ki分别为PI 控制器的比例和积分参数；角标1 和2 则分别为该控制参数属于电压外环和电压内环；和d*分别为滤波电感电流和移相占空比参考值；Zu和Zi分别为电压外环PI和电流内环PI输出的中间状态变量。

将变换器调制过程视为单位增益惯性环节，则有：

式中：Tδ为控制器延时；d为移相占空比；s为微分算子。

联立式（11）—（14），线性化后可得式（16）所示PSFB 全阶小信号模型。图4 进一步给出了小信号模型的完整框图，其中低通滤波器GLP(s)可按实际需要添加，且负载电路阻抗传递函数GL（s）可简化表达为：

图4 PSFB变换器全阶小信号模型Fig.4 Full-order small-signal model of PSFB converter

式中Gv（s）=Kp1+Ki1/s和Gi（s）=Kp2+Ki2/s分别为电压外环PI传递函数和电流内环PI传递函数。

式中：含Δ符号的变量代表对应变量的小扰动；含有角标0的变量代表对应变量的稳态值。

2.2 阻抗降阶建模

对于图4 所示全阶小信号模型，无论使用状态空间法还是阻抗法进行系统稳定性分析都是复杂的，且不利于后续有源阻尼控制策略的推导。为降低状态量之间的耦合性，将图4 中红色虚线框部分逐一定义为环节J1—J6，并作为备选的忽略环节，式（16）中相关的主电路方程可被重新描述为：

以降阶后振荡模态变化量小和状态量耦合性低作为目标，忽略某备选环节的振荡模态变化量可通过相应灵敏度进行估计。此时，系统状态空间矩阵为：

式中：Δx=［Δup，Δuf，Δis，Δif，ΔiL，Δzu，Δzi，Δd］；Δu=；A、B分别为系统矩阵和控制矩阵，其元素与式（16）和式（17）各状态量系数相对应。由于A阵各特征值λi（i=1，2，…，8）为系统的各振荡模态，则各振荡模态对J1—J6的灵敏度为：

式中：A11=J1J5/Cp，A14=J1J6/Cp，A17=J1/Cp，A41=J4/Lf，A44=J6J3/Lf，且A47=J3/Lf。

以表1 所示PSFB 变换器及其控制参数为例，考虑灵敏度和系数大小，最终选择忽略J2、J5、J6环节作为化简方案。图5 所示为简化前后系统特征值的对应关系，实际上为保证简化小信号模型低频段可行，靠近虚轴处的特征值差异应尽可能小，可以看出忽略J2、J5、J6时特征值与原始系统的特征值位置几乎一致。

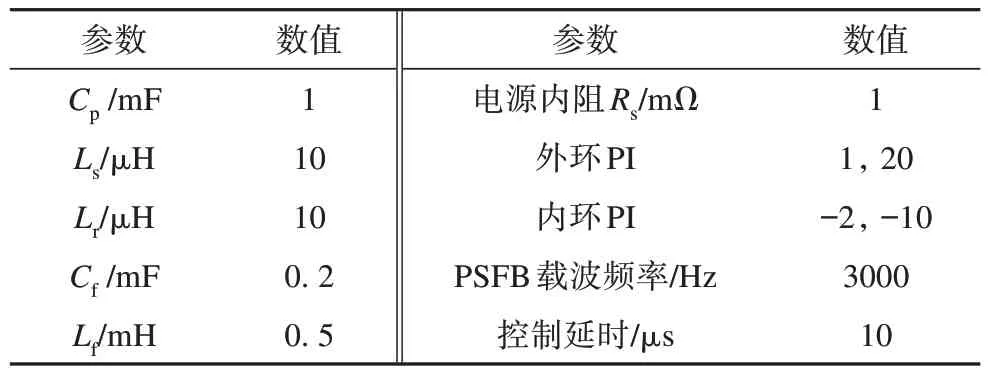
表1 PSFB变换器电路及控制参数Tab.1 Circuit and control parameters of the PSFB converter

图5 两种简化方式下振荡模态变化量对比Fig.5 Oscillation modal variations in two simplified methods

为进一步说明所选化简方案的依据，图6 对比了两种简化方式下的PSFB 变换器输入阻抗，可以看出忽略J2、J5、J6后的PSFB 变换器阻抗仅在500～600 Hz 时存在微小差异。结合图4，可得图7 所示降阶小信号模型，则PSFB 变换器源侧输入、输出阻抗降阶表达式分别为ZL（s）和Zo（s）。

图6 两种简化方式下阻抗曲线对比Fig.6 Comparison of impedance curves in two simplified methods

图7 有源阻尼补偿环节示意图Fig.7 Sketch diagram of active damping compensator position

3 PSFB负载变换器有源阻尼控制

3.1 输入电压前馈有源阻尼控制策略

有源阻尼策略一般通过在控制环路中注入补偿信号实现系统中虚拟阻尼支路的增加。若以抑制源侧直流配电系统为目标，则理想的阻尼支路配置应为图3 位置①。基于图7，假设Δus为0，图3 位置①引入虚拟阻尼支路Rvir1，推导源侧电容电压反馈补偿环节的基本形式为Mk1(s)与另一物理环节余项，如图7 红色实线框所示。考虑到物理电路部分小信号框图一般不变，故仅保留控制器部分所实现的效果。

此时Mk1(s)如式（22）所示，而小信号模型主要反映系统的低频特性，但仅影响Mk1(s)的高频特征，故将该环节简化为单位增益，即：

需要指出：若仅保留式（22）的高通特性，可进一步将其简化为一阶高通滤波器，从而减少补偿环节的参数量，降低设计的复杂度。

3.2 输出电压反馈有源阻尼控制策略

由于PSFB 变换器源侧一般为高压侧，采用输入电压前馈有源阻尼控制策略会导致额外的采样和测量成本。因此，本节尝试利用PSFB 变换器已有负载侧电容电压量测实现输出电压反馈的阻尼控制策略。为进一步阐述负载侧虚拟阻尼支路Rvir2与源侧虚拟阻尼支路Rvir1之间的关联性，将源侧电容右侧等效为负电阻，并代入Rvir1进行归算，则PSFB变换器引入虚拟阻尼支路Rvir1后的等效输入电阻Req可视为：

可知源侧电容处并联虚拟电阻对系统低频等值阻抗的影响，近似于负载侧产生ΔP0=的功率变化。若在负载侧电容上引入并联虚拟电阻Rvir2以同等减少这部分功率，即：

此时，输入与输出侧并联虚拟电阻满足：

基于图7 采用输出电压反馈的有源阻尼策略补偿环节Mk2（s）可设计为：

式中电源滤波电路阻抗传递函数Gs（s）和中间等效传递函数Gc（s）的表达式由式（28）给出。

忽略图7 中负载侧电压对电流内环的反馈，则代表框图蓝底部分的整体传递函数Gp(s)可视为一个不完整的电流环，其表达式为：

考虑到电流内环的带宽配置常远大于电压外环，故Gp(s) 可视为单位增益，则式（27）可简化为：

式中：Ak2为增益系数，Ak2=1/Rvir2Kp1；ωk2为转折频率，ωk2=Ki1/Kp1。

需要指出：1）虽然不同类型负载变换器的控制环路存在差异，但基本都以输出电压作为控制对象，因此本文提出的输出电压反馈阻尼控制策略及其推导过程理论上仍然具备适用性。2）接入场景（尤其是VSC 换流站主从、下垂等不同类型控制策略）以及负载变换器自身输出/输入阻抗会影响本文策略的应用，此时补偿器参数需要针对性调整。

4 算例验证与分析

为验证上述分析结论与有源阻尼补偿环节的有效性，以图8 所示双端直流配电系统为测试对象，其中各换流站采用三电平VSC 与伪双极接线方式，换流站1 采用定电压控制，换流站2 采用定功率控制，PSFB 变换器采用定负载侧电压控制。直流网络电压等级为±10 kV，负载侧电压为6 kV，系统参数除表1外，其余见表2。

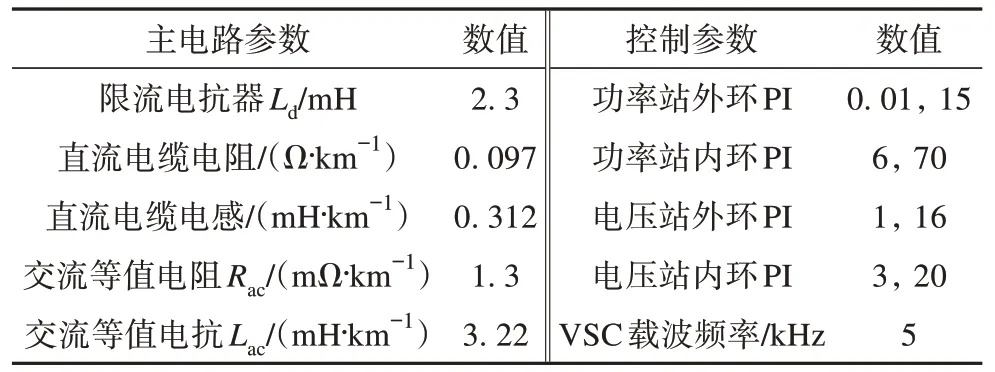
表2 直流配电系统电路及控制参数Tab.2 Circuit and control parameters of the DC distribution system

图8 双端直流配电系统结构图Fig.8 Structure of dual-terminal DC distribution system

4.1 阻抗降阶模型准确性验证

若负载电阻RL=2.5 Ω，以电磁暂态仿真阻抗扫频结果为参照，图9 为无补偿环节的降阶输入阻抗波特图，图10 为有补偿环节后的对比结果。可见，在1～1 500 Hz 的频率段内，所建立的输入阻抗降阶模型与扫频结果具有强一致性，能确保用于系统稳定性分析的准确性。图11 展示了引入式（31）所示补偿环节Mk2（s）前、后PSFB变换器输出阻抗。

图9 无补偿环节PSFB阻抗降阶模型与扫频结果对比Fig.9 Comparison of impedances between reduced-order impedance model and sweep frequency results for PSFB converter without compensator

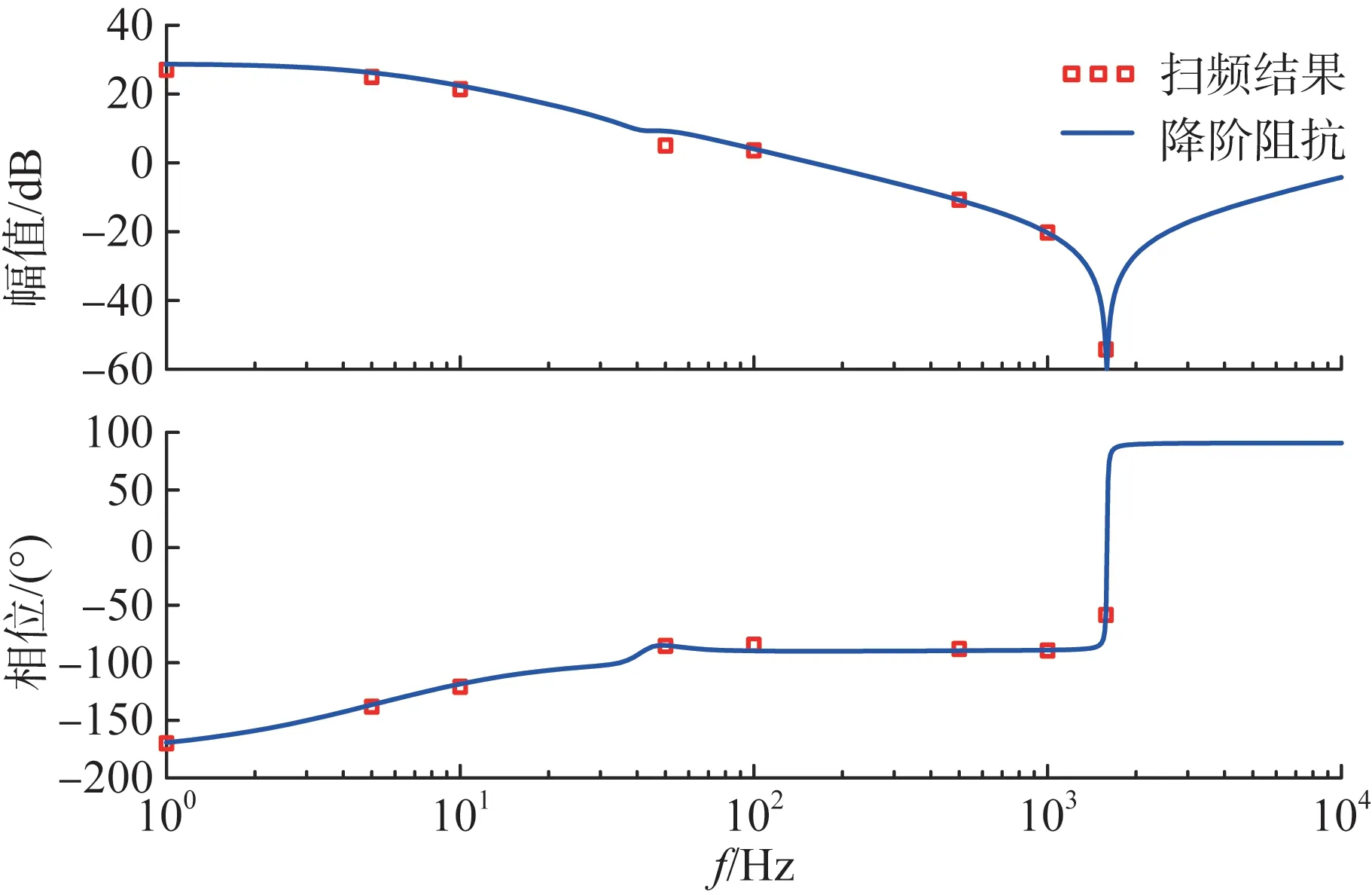
图10 有补偿环节PSFB阻抗降阶模型与扫频结果对比Fig.10 Comparison of impedances between reduced-order impedance model and sweep frequency results for PSFB converter with compensator

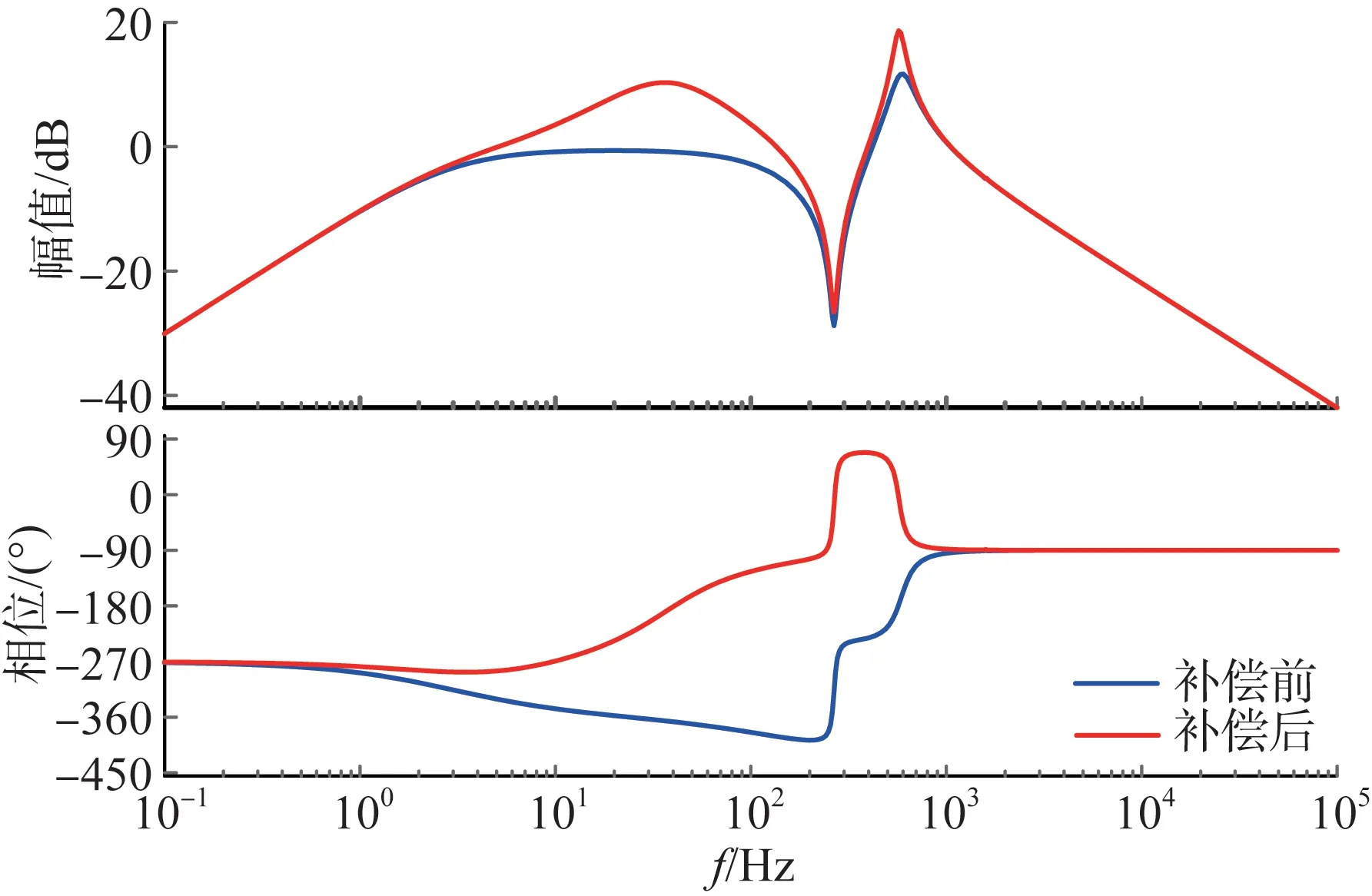
图11 补偿前后PSFB变换器输出阻抗比较Fig.11 Comparison of PSFB converter equivalent output impedances with and without compensator

4.2 补偿环节有效性仿真验证

若使P1和P2分别表示定功率站和PSFB 变换器的运行功率，则在P1=21.5 MW，P2=18 MW 与P1=25 MW，P2=14.4 MW 两种工况下，添加补偿环节Mk2（s）前后系统特征值变化如图12所示，即添加补偿环节后系统稳定性得到增强。

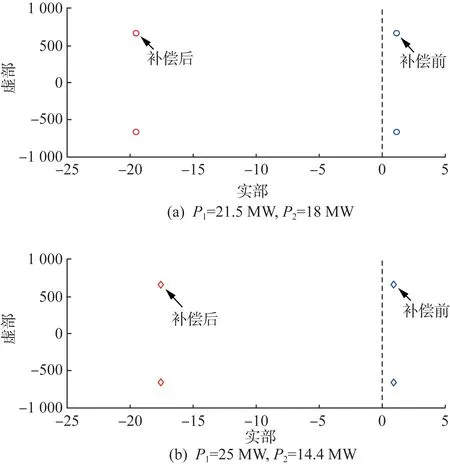
图12 补偿前后系统主导特征值Fig.12 Dominant eigenvalue of the system with and without compensator

基于上述分析，让定功率站在2.5 s 由吸收21.5 MW 功率阶跃到吸收25 MW 功率，此时直流母线电压振荡失稳，当在3 s 投入式（30）所示输出电压反馈补偿环节后，直流母线电压电流振荡收敛并最终稳定，如图13 所示。若定功率站吸收21.5 MW 功率时，PSFB 变换器增加600 A 恒流源负载，此时直流母线电压电流也将振荡失稳，当在3 s 投入式（31）所示输出电压反馈补偿环节后，直流母线电压电流同样振荡收敛且稳定，如图14 所示。类似地，结合式（26）推导出式（31）对应的输入电压前馈有源阻尼补偿环节Mk1（s）为：

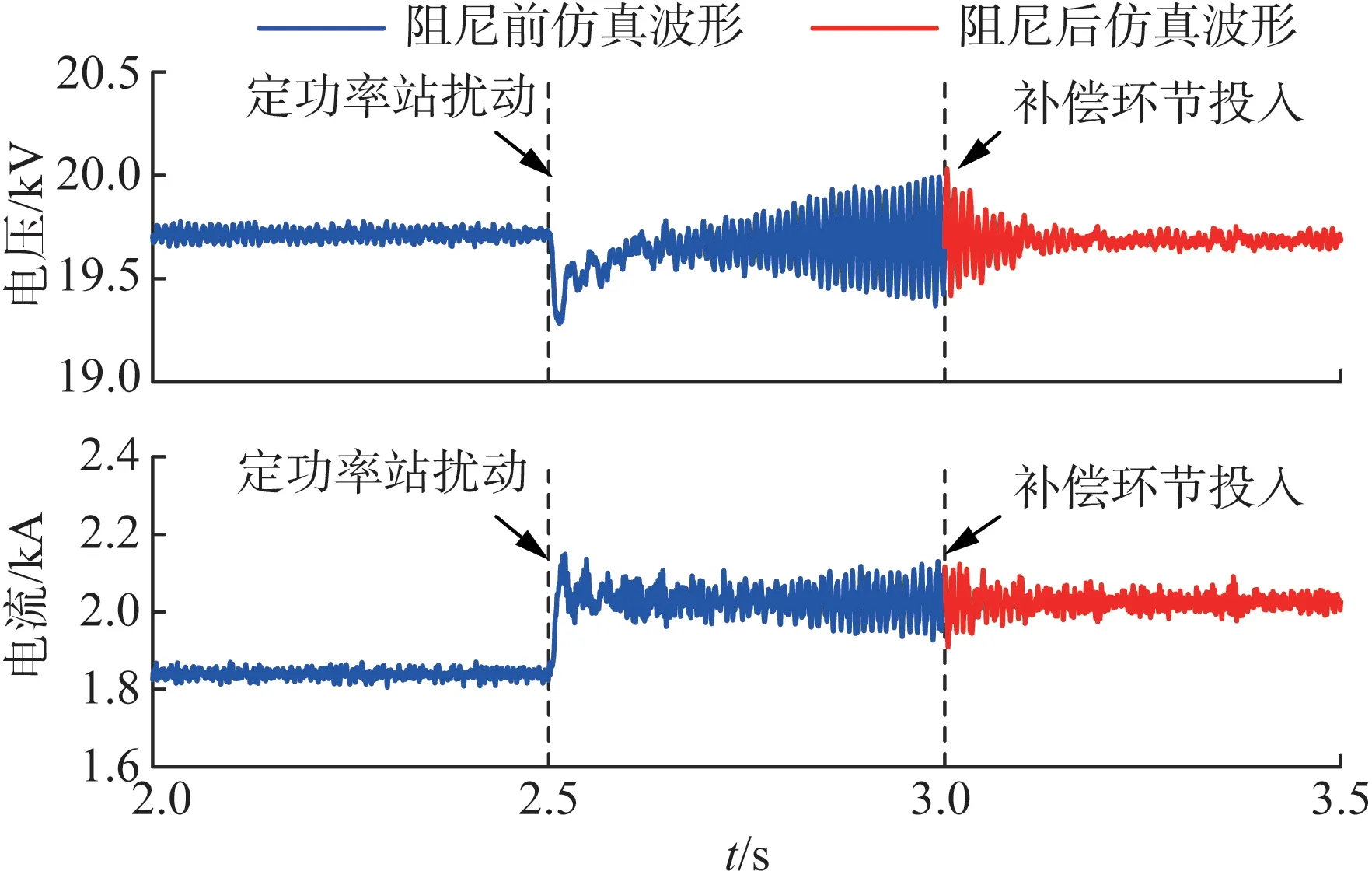
图13 定功率站扰动下的失稳抑制（投切Mk2）Fig.13 Instability suppression under the disturbance of constant power stations（using Mk2）

图14 PSFB变换器扰动失稳抑制（投切Mk2）Fig.14 Instability suppression under the disturbance of PSFB Converter（using Mk2）

此时，对比图13 和图14 两种工况，投切有源阻尼补偿环节Mk1（s）时的电压、电流响应波形分别为图15 和图16。可知，当采用输入电压前馈补偿环节时，同样能够抑制系统振荡，且两种补偿环节可以基于式（25）进行近似换算。因此，PSFB 变换器有源阻尼策略不仅对自身的振荡具有抑制作用，还可用于阻尼系统中其他换流器诱发的振荡。

图15 定功率站扰动下的失稳抑制（投切Mk1）Fig.15 Instability suppression under the disturbance of constant power stations（using Mk1）

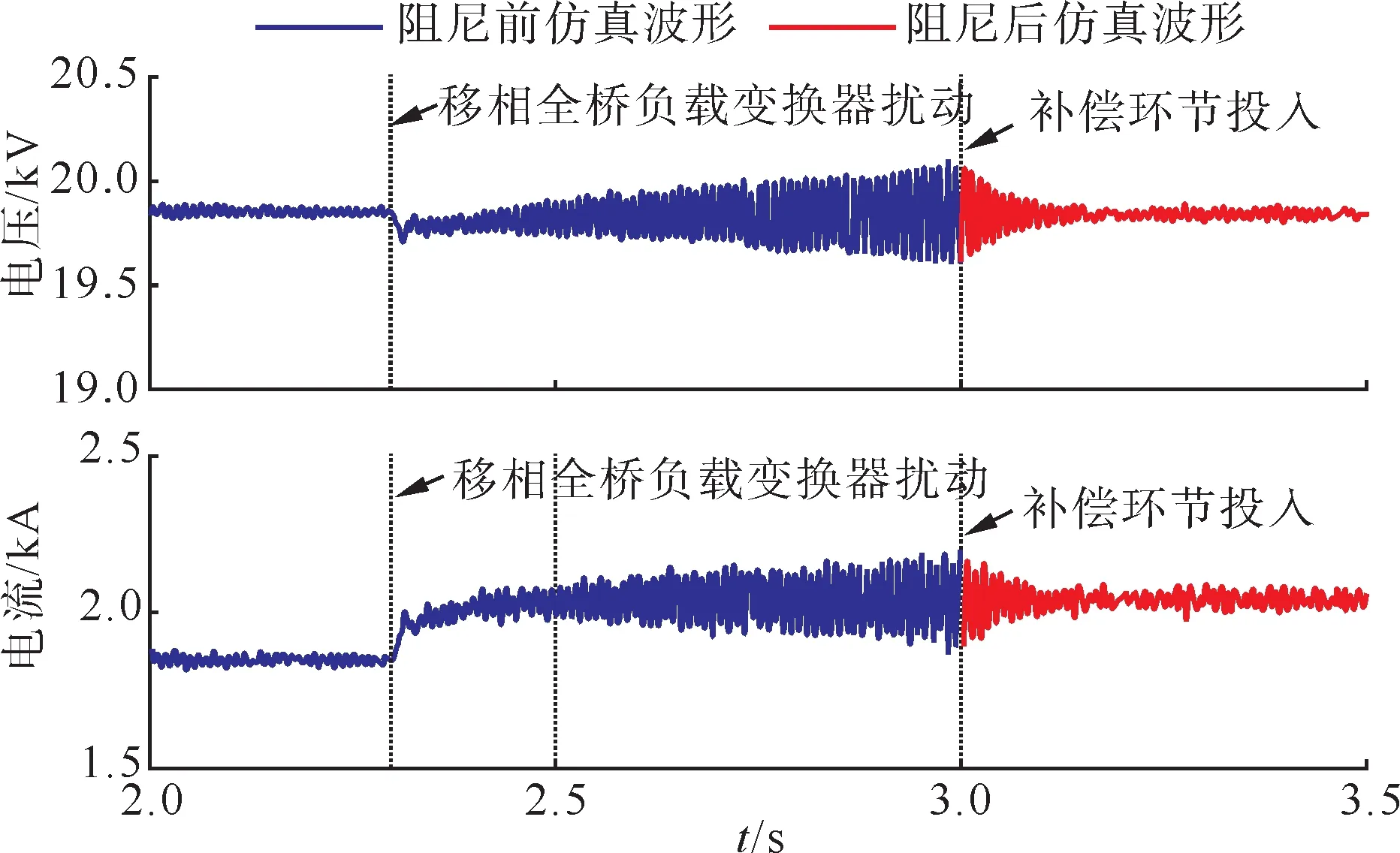
图16 PSFB变换器扰动失稳抑制（投切Mk1）Fig.16 Instability suppression under the disturbance of PSFB converter（using Mk1）

4.3 硬件在环实验验证

为进一步验证阻尼策略的实际应用效果，基于RT-LAB和DSP+FPGA 数字控制器搭建了硬件在环实验平台。受限于可用数字输出通道数量，仅对PSFB 变换器控制进行实际控制器实现，同时考虑到RT-LAB 仿真步长的限制，仿真步长设定为20 μs，而电路参数及控制参数保持不变。

以定功率换流站阶跃5 MW 为例，图17 与图18 分别为PSFB 配置有源阻尼补偿环节Mk1（s）前后的母线电压、电流波形。硬件在环实验结果表明其与 Simulink 离线仿真具有一致性，说明了所提输出电压反馈有源阻尼控制策略在极限传输功率提升和系统振荡抑制方面的有效性。

图17 定功率站扰动下实验波形（未启用Mk1）Fig.17 Experimental waveforms under the disturbance of constant power stations（without Mk1）

图18 定功率站扰动下实验波形（启用Mk1）Fig.18 Experimental waveforms under the disturbance of constant power stations（with Mk1）

5 结论

本文建立了PSFB 变换器阻抗降阶模型，采用并联虚拟阻尼支路对PSFB 输入电压前馈与输出电压反馈两类补偿环节进行了溯源推导，并提出了两种有源阻尼控制策略［26］。最后，通过双端直流配电系统的MATLAB/Simulink 时域仿真模型和硬件在环实验验证了所提PSFB 变换器阻抗降阶模型的准确性和有源阻尼策略的有效性［27］，结论如下。

1）基于平均变量等效电路搭建的PSFB 阻抗降阶模型与电磁暂态模型阻抗特征具有强一致性，确保了阻抗降阶模型用于稳定性分析的可靠性。

2）不同形式和参数的有源阻尼补偿环节均可对应PSFB 变换器的某一虚拟阻尼支路，并同时对PSFB变换器的输入、输出阻抗特性造成影响。

3）多端系统中有源阻尼控制策略不但可以抑制被补偿变换器引发的失稳振荡，还可以抑制由其他换流器诱发的振荡。