计及多元不确定性的氢电耦合微电网多阶段动态规划方法

王笑雪，高 超，刘一欣，梁 栋，侯世昌

（1.河北工业大学 省部共建电工装备可靠性与智能化国家重点实验室，天津 300130；2.天津大学 智能电网教育部重点实验室，天津 300072；3.国网冀北电力有限公司 秦皇岛供电公司，河北 秦皇岛 066000）

0 引言

微电网是集成多种分布式能源（distributed energy resource，DER）、储能系统（energy storage system，ESS）和负荷的小型发-配-用电系统，是优化能源结构、提高可再生能源渗透率的有效手段［1-2］。近年来，氢能发展得到了广泛关注，以分布式可再生能源制氢［3-4］、就近用氢［5］的氢电耦合微电网成为促进氢能发展和利用的一种新模式［6-7］。

投资经济性是影响氢电耦合微电网发展和推广应用的主要因素之一，也是微电网规划设计重点关注的问题之一。如何兼顾规划方案在投资成本、回收期、能源利用率等方面的综合表现，优化DER 长期投资决策和短期运行调度，是规划设计问题的核心难点。文献［8］基于偏远矿山的能源基础设施，针对微电网的规划与运行问题提出了一种分层决策模型，使2 个问题的决策变量得到独立优化；文献［9］提出了一种随机规划方法，考虑了新能源发电的不确定性，并引入燃料电池和电解水制氢提高系统对新能源的消纳能力；文献［10］在规划中考虑了燃料电池和电解水制氢系统的启停和退化，构建了包含冷、热、电和氢气的微电网混合整数线性规划模型；文献［11］在微电网规划设计问题中考虑了负荷需求等的不确定性，以确定DER 的类型、容量以及相应的最优运行策略；文献［12］提出了一种包括光伏、风机、沼气发电机和燃料电池的混合可再生能源系统，所提规划模型使系统在灵活性和能源利用率两方面都得到了提高；文献［13］考虑了网络拓扑、DER 容量、发电和需求的随机性，以最大限度降低微电网的投资、运营成本为目标构建了规划框架，并将其表述为混合整数非线性规划问题。上述研究提出了具有不同目标和约束的微电网经济规划方法，为微电网建设提供了有效的经济决策支持。然而，上述研究采用了单阶段规划模型，所有DER 均在规划周期的第一年进行投资建设。换言之，此类模型确定的投资决策包括DER 类型、规模或系统结构，但未考虑DER 的最佳投资时机。为应对未来可能的负荷增长，该规划方案可能会导致微电网初始阶段的容量冗余，造成不必要的能源浪费。此外，较高的初始投资成本也会给投资者带来巨大的财务负担。另一方面，随着光伏、储能等单位投资成本逐年降低，以动态规划视角考虑DER 在未来不同阶段的投资方案，有利于实现更好的源-荷匹配，提升长周期投资经济性。为此，文献［14］提出了一种多阶段随机优化模型，证明了多阶段投资具有更好的经济性，文献［15］提出了一种多阶段自适应规划方法，在得到与传统多阶段规划方法相似的投资决策前提下，具备更高的计算效率，然而文献［14］和文献［15］均未考虑源荷短期运行的不确定性。文献［16］针对独立型微电网提出了一种多阶段投资规划模型，考虑了可再生能源发电和负荷需求的不确定性，但是未考虑设备投资成本的不确定性。

本文提出了一种氢电耦合微电网多阶段动态规划模型，考虑了规划周期内光伏、电储能、燃料电池和电解水制氢单位投资成本的随机不确定性和光伏出力与负荷需求的不确定性，建立了随机-鲁棒混合多阶段规划模型。此外，考虑了光伏、电储能、燃料电池和电解水制氢系统的退化以及负荷增长等动态信息，从动态视角实施投资决策，使模型更具实用性。仿真结果表明，与单阶段规划模型相比，所提模型在投资成本、投资回收期、能源利用效率等方面均有显著改善。

1 氢电耦合微电网多阶段规划模型

本文设计的并网型氢电耦合微电网结构如图1所示，由光伏、电解水制氢、燃料电池、电锅炉、ESS和负荷构成，其中ESS 包括电储能、储氢罐和储热罐，负荷包括电负荷、氢负荷和热负荷。

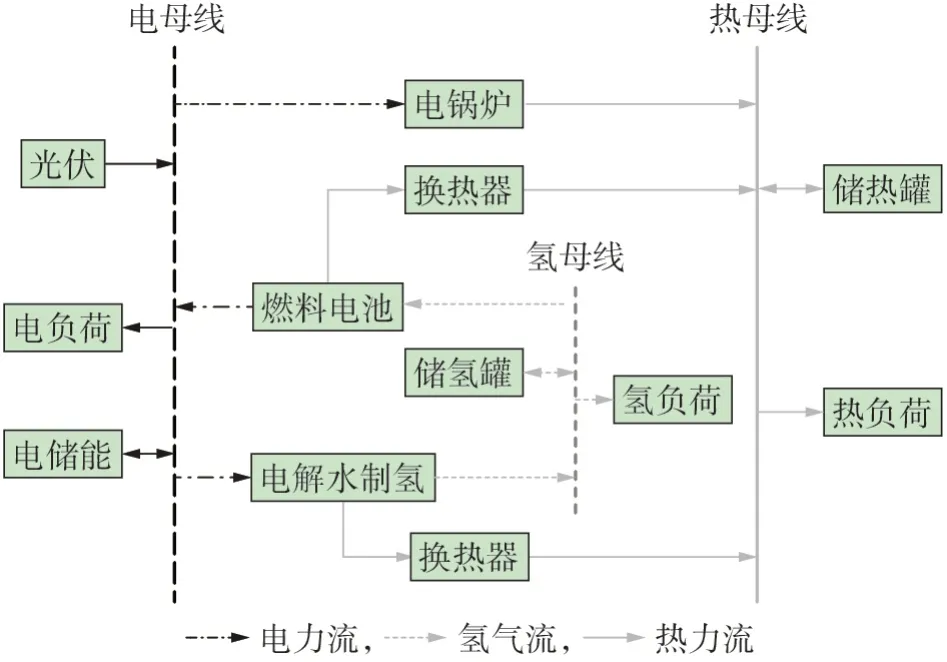
图1 氢电耦合微电网结构Fig.1 Structure of hydrogen-electric coupled microgrid

针对图1 所示的微电网，多阶段规划模型的目标函数如式（1）所示，包括各设备的投资成本Cinv、运维成本Com和残值Csal，其计算公式分别如式（2）—（4）所示。

式中：PV、 FC、 EZ、 EB、HeatS、 BAT、 HS 分别表示光伏、燃料电池、电解水制氢、电锅炉、储热罐、电储能、储氢罐；为设备k第n年的最小单元装机个数；为设备k的最小单元容量为设备k第n年的单位投资成本；NY为规划周期；rloan为贷款比例；SAIR为贷款年利率；r为折现率；Nloan为贷款年限；c和c分别为设备k1的单位运维成本和设备k2的单位运维成本；为设备k2第n年的有效容量；D为典型日集合；T为调度时段集合；ωn，d为第n年典型日d对应的权重系数；P和P分别为第n年典型日d下t时段的购电功率和售电功率；和分别为第n年典型日d下t时段的购氢体积和售氢体积；c和c分别为单位购电价格和售电价格；c和c分别为单位购氢价格和售氢价格；c和c分别为设备k1的单位容量残值和设备k2的单位容量残值。

为了计及规划周期内设备性能衰减的影响，提升规划方案对未来动态因素的适应性，本文在多阶段规划中考虑了光伏发电效率衰减约束（如式（5）所示）、燃料电池和电解水制氢峰值功率退化约束（如式（6）所示）和效率衰减约束（如式（7）所示）［17］。式（8）和式（9）分别表示计及效率衰减后燃料电池的氢-电转换和电解水制氢的电-氢转换关系。其余约束，如氢、热、电功率平衡约束和设备运行约束等具体见附录A。

相比于其他设备，电储能的使用寿命较短，因此除上述运行约束外，规划模型中还需考虑电储能的寿命约束。电储能的寿命可以用其全寿命周期的放电量来表示，当电储能累计放电量达到最大放电量时认为电储能寿命耗尽［16］，需要用新的电储能进行更换。计及电储能寿命约束的公式如下：

由于式（10）—（12）中存在二进制变量和连续变量的乘积项，因此引入L1n—L3n这3 个辅助变 量对其分别进行线性化处理：

结合式（13）—（15），将辅助变量代入式（10）—（12）中可得：

综上，氢电耦合微电网多阶段动态规划模型的变量可归纳为：

式中：x和y分别为由与规划层面和调度运行层面相关的变量组成的向量；和分别为第n年典型日d下t时段的光伏发电功率、电储能充电功率、电锅炉耗电功率和电负荷；和分别为第n年典型日d下t时段储氢罐充、放氢体积和氢负荷和分别为第n年典型日d下t时段燃料电池发电余热量、电解水制氢余热量、电锅炉产热量、储热罐蓄热量、储热罐放热量、弃热量和热负荷；分别为第n年典型日d下t时段电储能、储氢罐和储热罐的剩余存储容量；分别为第n年典型日d下t时段储氢罐充、放氢的摩尔流量；为第n年典型日d下t时段的储氢罐压力。为了更清楚地描述模型，本文给出了多阶段规划模型的紧凑形式，如下所示：

式中：c和d为目标函数式（1）的系数列向量；A、B、Q、G、W、F、M、R和I为各约束条件对应的变量系数矩阵；a、b、q、g、h和m为常数列向量；û如式（21）所示。约束条件中，Ax≥a对应式（13）—（16）、（18）；Bx=b对应式（17）；Qy≥q对应附录A 式（A7）、（A15）—（A18）；Gy=g对应式（7）—（9）和附录A 式（A1）—（A4）、（A6）、（A8）、（A13）；Wy≥h-Fx对应式（6）和附录A 式（A5）、（A10）—（A12）、（A14）；My=m-Rx对应附录A式（A9）；Iy=û对应式（5），表示各时段光伏出力和负荷需求等于其预测功率。

2 氢电耦合微电网随机-鲁棒动态规划模型

在动态规划模型中，设备的成本是影响投资经济性的主要因素之一。随着制造工艺的进步，设备的价格整体上呈下降趋势，但依然受一些不确定性因素的影响，成本存在一定随机波动性。为此，以对数正态分布拟合光伏和电解水制氢系统的单位投资成本［19-20］，以正态分布［21］和三角形分布［22］分别描述电储能和燃料电池投资成本的不确定性，最终通过蒙特卡罗抽样和聚类压缩得到设备逐年投资成本的随机概率场景。考虑投资成本不确定性后，式（2）转换为如下形式：

式中：Cinv，n为第n年各设备的投资成本；k∈{PV，BAT，FC，EZ}；ωs为场景s发生的概率；S为场景集；为第n年设备k在场景s下的单位投资成本。

此外，日内光伏出力和负荷需求不确定性以如下箱形不确定集合U描述：

式中：u为由不确定变量组成的向量；u和u分别为第n年典型日d下t时段的光伏出力和负荷功率；ΔP和ΔP分别为光伏和负荷预测功率的最大偏差；ΓPV和Γload分别为光伏和负荷不确定性调节参数，用于调整规划方案的保守性［1］。

综上，构建如下随机-鲁棒混合多阶段动态规划模型：

式中：E(cTx)为投资成本的期望值；Ω（x，u）为y的可行域。在式（24）中，外层为最小化问题，其中x是与规划决策相关的第一阶段向量，满足设备投资成本随机场景下总成本的期望值最小，内层为最大／最小化问题，可确定光伏出力和负荷需求的最恶劣场景，y和u是与运行决策相关的第二阶段向量。

结合式（19）、（22）、（24）可知，本文所构建的规划模型中，设备k第n年的投资容量Xkn为决策变量，其表征微电网投资主体将设备的投资由传统的第1年全部投入转变为“多阶段”执行。在此架构下，投资主体可基于设备k第n年单位成本、第n年负荷需求、分布式电源发电等信息，全面评估第n年投入设备k的价值，进而决定设备k的逐年投资方案，从而优化微电网每年的源荷匹配，提升规划方案的经济性。

多阶段规划模型可通过列与约束生成（column and constraint generation，C&CG）算法进行求解［16］。具体步骤如下：

1）根据光伏、电储能、燃料电池和电解水制氢的预测成本数据以及成本分布模型，通过蒙特卡罗模拟生成价格场景，并采用K-means 聚类法减少场景数量，得到价格场景及相应的权重系数ωs；2）基于文献［23］所提典型日选取方法，考虑规划期内负荷增长率和光伏衰减率，得到规划期内的典型场景和相应的权重ωn，d；

3）给定一组u值作为初始的最恶劣场景，设置下界值SLB=-∞、上界值SUB=∞以及迭代次数l初始值为1，根据最恶劣场景下的u求解主问题，并用主问题的目标函数值更新SLB；

4）将第l次迭代时主问题的解代入子问题进行求解，得到子问题最优值，更新上界SUB=

5）设置收敛阈值ξ=0.01，若(SUB-SLB)/SLB≤ξ则停止迭代，否则在主问题中引入新的割约束式（25），更新l=l+1，并重新求解主问题，更新下限SLB，跳转至步骤4）进行迭代求解直到算法收敛。

式中：α为辅助变量。

3 算例分析

本文将微电网规划周期设置为10 a，并设置系统的折现率为5 %［16］，贷款利率为6.5 %［16］，贷款年限为6 a，负荷增长率为3 %［24］，其余主要参数见附录B表B1。

BIM在施工过程中的质量控制的最大优点，就是提高了施工单位项目部内部班组实施质量信息的沟通效率，而且大大改善了施工单位与其他项目参与方的沟通组织及协调。基于BIM沟通，不管你在哪里，都能随时随地检查质量信息，移动端就能发出指令要求，就能要求整改并上传质量信息。坐在办公室的项目领导只需打开相关系统及软件，就能够实现查阅质量信息及发布远程管理指令，便于工程项目的远程管理、控制及组织协调。

以文献［25-27］中光伏、电储能、燃料电池、电解水制氢设备未来逐年单位投资成本预测为基准值，基于文献［19-22］构建的各设备投资成本分布模型（如附录B表B2所示），由蒙特卡罗模拟得到1 000个随机场景，并采用K-means 聚类法进行场景压缩，通过误差平方和（sum of squared error，SSE）确定场景数量，如附录B图B1所示。可以看出，SSE随着聚类数的增加而减小，当聚类数大于20 时，下降速度变得十分缓慢。因此，本文选取20 个随机场景以平衡准确性和计算效率，对应20 个光伏、电储能、燃料电池和电解水制氢未来的单位成本场景，如附录B 图B2 所示，其中每个场景发生的概率如附录B 表B3所示。C&CG 算法的收敛迭代过程如附录B 图B3所示。

3.1 规划结果分析

为了验证本文所提方法相比于单阶段规划方法以及未考虑投资成本不确定性的多阶段规划方法的优势，设置如下案例：

案例1，投资决策采用传统的单阶段规划模型，考虑设备的退化，负荷增长率设为3 %；

案例2，投资决策采用多阶段规划模型，考虑设备的退化，但不考虑投资成本不确定性（即不考虑投资成本的波动情况），负荷增长率设为3 %；

案例3，投资决策采用本文提出的多阶段规划模型，负荷增长率设为3 %；

案例4，投资策略与案例1 相同，负荷增长率设为4 %；

案例5，投资策略与案例3 相同，负荷增长率设为4 %。

图2、3 和附录B 图B4 分别展示了案例1 — 5 下DER 和ESS 的投资容量及投资时间、累计净现值和光伏本地消纳率。其中，光伏本地消纳率指光伏自发自用部分电量与光伏总发电量的比值。从图2 中可以看出，在相同负荷增长率下，多阶段规划模型的初始配置容量均低于单阶段规划模型，且考虑投资成本不确定性后的多阶段规划模型的初始配置容量更低。以负荷增长率为3 % 为例，本文提出的模型（案例3）相比于单阶段规划模型（案例1），光伏、电储能、燃料电池、电解水制氢、电锅炉、储热罐和储氢罐的初始投资容量分别降低了15.4 %、11.1 %、1.4 %、13.7 %、3.3 %、10.8 %、1.2 %；与此同时，相比于未考虑投资成本不确定性的多阶段规划模型（案例2）分别降低了5.4 %、6.2 %、0.7 %、12.6 %、1.1 %、7.3 %、0.6 %。另外，由图3 可知，采用本文提出的模型能在满足规划初期负荷需求的前提下，显著降低初始投资成本。

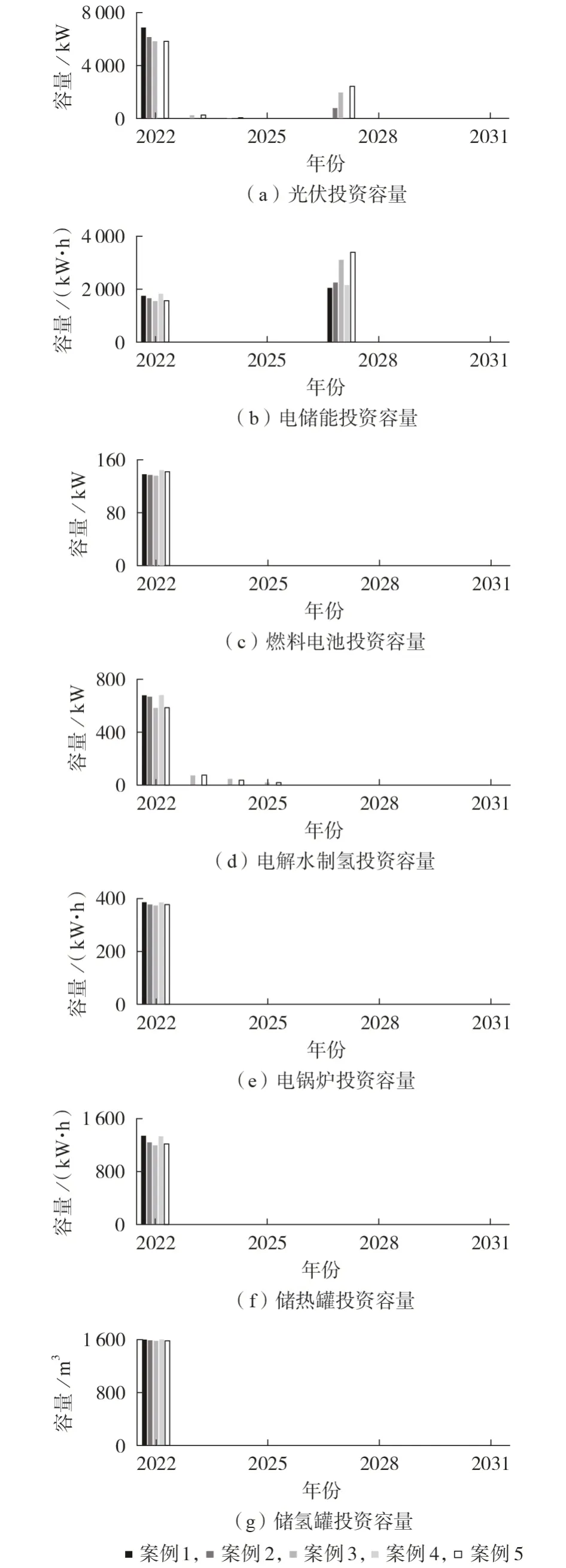
图2 案例1— 5的投资规划方案Fig.2 Investment planning schemes of Case 1-5

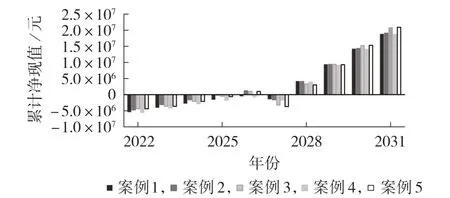
图3 案例1— 5的累计净现值Fig.3 Cumulative net present values of Case 1-5

此外，本文提出的多阶段规划模型将光伏和电解水制氢设备的投资分布在未来多个阶段，有效利用了设备成本降低的趋势，提升投资经济性。案例2 虽然同样采用多阶段投资策略，但未能充分利用设备成本波动特性，在2027 年投入光伏容量较低。相较而言，本文方法在2027 年增加了较大容量的光伏和电池配置，以提升后续阶段微电网运行的经济性。从图B4中可以看出，多阶段规划模型在初期光伏本地消纳率更高，源荷匹配性更强。在2027 年由于新增较大容量光伏，微电网上送电量增加，导致本地消纳率有所降低。此外，图2（b）中案例1 在2027年也配置了储能，这是因为单阶段规划模型同样考虑了电储能寿命约束式（10）—（12），因此在2027 年需要进行电储能替换。

假定贷款比例设置为0.8，案例1 — 5 的投资决策及成本如表1 所示。其中，投资回收期是指未来现金净流量的现值等于原始投资额现值时所经历的时间。可以看出，案例3和案例1相比总投资成本降低了近5.0 %，初始投资成本降低了近13.9 %，投资回收期缩短了近32.9 %。且随着负荷增长率的提高，多阶段规划模型初始投资成本降低的百分比进一步提升。这是因为随着负荷增长率的提高，单阶段规划模型将提高初始光伏／储能配置容量，以满足未来负荷增长需求。然而，在本文提出的多阶段动态投资策略下，负荷增长导致的容量需求将在未来以最经济的方式进行优化，因此光伏／储能的初始配置容量几乎相同，有利于缓解初期的资金压力，降低借贷成本。此外，案例3和案例2相比总投资成本降低了近3.6 %，初始投资成本降低了近6.5 %，投资回收期缩短了近1.4 %，体现了在多阶段规划中考虑设备投资成本不确定性的价值。

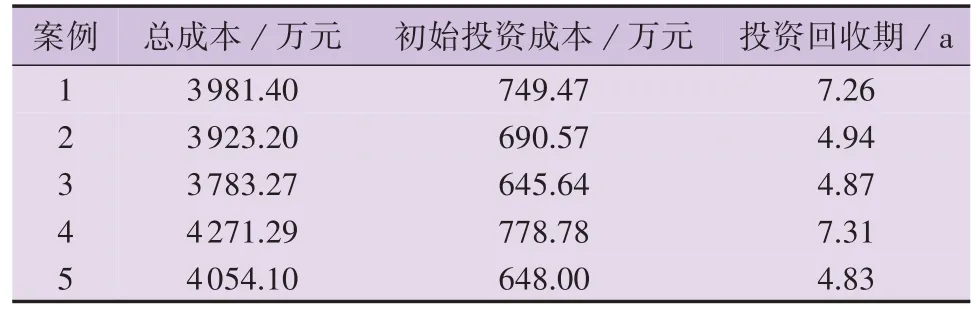
表1 案例1 — 5的投资决策及成本Table 1 Investment decision-making and costs of Case 1-5

此外，选取3 组不确定性调节参数分析其对规划方案保守性的影响，参数的选取以及规划总成本如表2所示，表中负值表示收益。

表2 不同不确定性参数下氢电耦合微电网的总成本和运行成本Table 2 Total costs and operation costs of hydrogen-electric coupled microgrid under different uncertain parameters

从表2 可以看出，随着不确定性调节参数的增大，氢电耦合微电网的总成本和运行成本均随之增加。换言之，微电网在制定日前调度计划时越多地考虑不确定性因素，得到的方案越保守，相应的规划周期内的总成本和运行成本也越高。通过灵活调整该参数，可实现对规划方案保守度的调整。

3.2 调度结果分析

以冬季某典型日的数据为例对调度结果进行分析。冬季24 h的购／售电价格和购／售氢价格如附录B 图B5 所示，某典型日下电、热、氢负荷如附录B图B6所示。该典型日的电、氢和热能流调度结果分别见附录B图B7 — B9，其中电、氢、热负荷对应的值是该典型日的最恶劣场景下的值。由图可知：［01:00，08:00）时段和24:00 时购电价格较低，微电网向电网购买电能，在满足电负荷需求的基础上，可以对电储能充电，也可以通过电解水制氢以及电锅炉产热分别满足氢、热负荷；［08:00，10:00）时段，光伏发电和电储能放电可满足电负荷需求，同时供给电解水制氢系统工作，产生的余热连同储热罐一同供给热负荷；［10:00，18:00）时段，光伏产生的电能充足，多余的电能可以供给电储能充电、电解水制氢和电锅炉产热，同时向电网出售富余的电能；［18:00，24:00）时段，由于电价较高，燃料电池和电储能发电满足电负荷需求，从而降低购电成本，并通过余热和储热罐放热满足热负荷需求、储氢罐放氢满足氢负荷需求。

4 结论

本文提出了一种氢电耦合微电网随机-鲁棒混合多阶段动态规划模型，所得结论如下。

1）所提模型综合考虑了规划阶段光伏、电储能、电解水制氢、燃料电池的投资成本不确定性以及运行阶段光伏发电和负荷需求不确定性。同时，模型计及了设备效率衰减、负荷增长等动态因素，确定最佳投资容量和时机，能够给投资者提供更加合理的投资决策。

2）所提模型以动态投资视角确定规划方案，可利用设备投资成本逐年降低属性，优化投资方案。在仿真案例中，与传统的单阶段投资规划模型相比，所提模型总成本降低了近5.0 %，初始投资成本降低了近13.9 %，投资回收期缩短了近32.9 %，具有较好的经济性。

附录见本刊网络版（http：//www.epae.cn）。