孤岛微电网中制氢负荷谐波功率分配策略

徐万万，王 斌，张良力，刘 江

（1.武汉科技大学 信息科学与工程学院，湖北 武汉 430081；2.武汉工程大学 电气信息学院，湖北 武汉 430205）

0 引言

21 世纪以来，全球变暖迫使能源低碳化转型，电-氢综合能源系统具有重要的环保和经济效益。将水电解制氢负荷与微电网相结合能够得到投资成本最低且灵活度最高的配置方案［1］。制氢单元由若干个电解槽单体组成，在电能、热能的作用下将水转化成氢气和氧气。为了实现电解槽的宽范围降压功能，电解电源通常由前级AC／DC 整流器和后级DC／DC 变换器组成，传统的大功率工业应用中采用6 脉波整流器和12 脉波整流器［2］，负荷特性包括瞬间大电流和非正弦周期性电流。因此，电-氢微电网中的谐波功率分配问题成为了新的研究难点。

针对非线性负荷引起的微电网中谐波功率分配问题，文献［3］提出了虚拟谐波电阻储能逆变器的控制策略，指出谐波控制不影响基波控制；文献［4］提出了自适应虚拟电阻方法，通过建立虚拟谐波阻抗与流入其谐波电流之间的代数关系，动态调整虚拟电阻值以实现均分；文献［5］提出了基于小扰动信号注入的自适应虚拟阻抗控制方法，通过检测注入微电网的小信号产生的有功功率来调整逆变器的虚拟谐波电抗，达到均分谐波功率的目的；文献［6］通过检测逆变器谐波功率分配偏差信号来设计触发控制，提出了一种分布式事件触发控制策略，并引入比例-积分控制来动态调整虚拟电感，在降低通信需求的基础上，实现了孤岛微电网功率的精确分配。然而，上述研究均以谐波功率在各逆变器间均分为目的展开，但在实际的微电网中，离谐波源电气距离近的变流器尽可能多地承担谐波电流，这有助于减小谐波的影响，所以谐波功率均分并不是必须的，只需要保证谐波功率不超过逆变器的剩余容量即可。当连接子网的优先级不同时，保证高优先级子网的电压质量比保证多台逆变器的公平性更有意义。

近年来，有学者基于虚拟阻抗控制的基本原理，提出了考虑微电网电压质量的谐波电流分配策略。文献［7］提出了一种自适应谐波阻抗重塑方法，实现了谐波电流按照容量均分，并提高了公共连接点处的电压质量；文献［8］基于两级式分层控制，提出了考虑电压质量问题的谐波功率均分策略；文献［9］针对母线2 倍交流电压频率的谐波分量，提出了基于启发算法抑制环流并补偿谐波电流的方法，但该方法仅适用于直流微电网。微电网的电压谐波补偿本质上是通过并联逆变器提供的低谐波阻抗通路来改变系统谐波潮流实现的。文献［10］采用虚拟负阻抗控制，并进一步根据各逆变器的剩余容量及谐波功率差值，对其负阻抗的大小进行下垂调节；文献［11］以改善电压质量为目标，提出了谐波功率分配策略，为谐波电流提供尽可能小的流通路径。

虽然上述方法对公共连接点处的电压质量具有一定的改善作用，但没有考虑子网优先级不同对电压质量的不同需求，且已有文献针对水电解制氢负荷的研究较少。为此，本文将文献［7］中所提谐波阻抗重塑方法拓展应用于考虑子网优先级的孤岛电-氢交直流混合微电网中，首先建立微电网、质子交换膜（proton exchange membrane，PEM）电解槽、功率转换系统的模型；然后，推导谐波视在功率的简化公式，以降低计算负担；最后，提出以保证高优先级系数子网电压质量为目标的谐波功率分配策略，在保证互联变换器（interlinking converter，ILC）不过载的基础上，基于重塑因子调整谐波阻抗，实现谐波功率在ILC 和交流子网之间的自适应分配策略。相比于文献［12］中的策略，本文所提策略不需要额外构造虚拟阻抗，硬件在环实验验证了本文所提策略的有效性。

1 考虑优先级的微电网功率协调控制

典型交直流混合微电网的拓扑结构由交流子网、直流子网、ILC 组成，制氢负荷接入交流母线，如图1所示。文献［13］将子网优先级分为3类，即具有关键负荷的A 类微电网、具有固定非关键负荷的B类微电网、具有非关键灵活负荷的C 类微电网，其中A 类子网的电压或频率偏差小于0.5 %，B 类子网的电压或频率偏差小于3 %，C 类子网的电压或频率偏差小于5 %。在此基础上，本文引入优先级系数ω，其代表各类子网的优先级，ω值越小，则子网的优先级越低。

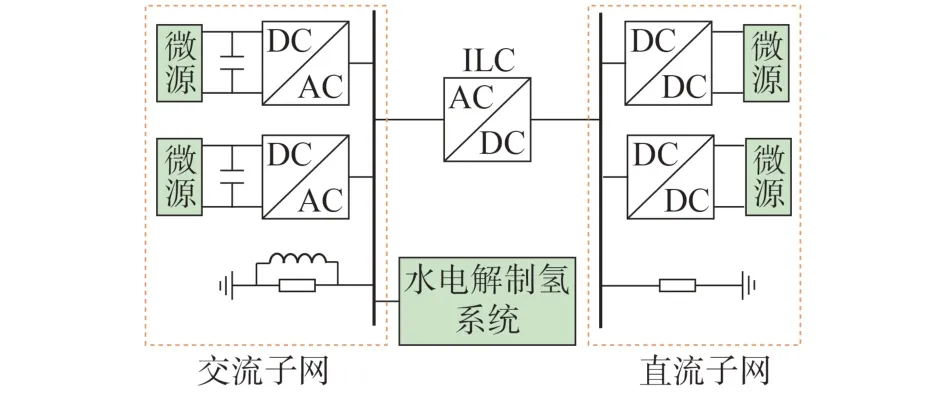
图1 混合微电网的拓扑结构Fig.1 Topology structure of hybrid microgrid

1.1 基于综合惯量的ILC控制

虽然低压微电网中的线路阻感比较大，但在LCL滤波器网侧电感的影响下，ILC连线阻抗以感性为主，根据交流、直流下垂控制策略，模拟交流子网的输出频率fac、交流电压Uac和直流子网的直流电压Udc，如式（1）所示。

式中：m、n分别为交流子网P-f、Q-U下垂系数；Pac，d、Pdc，d分别为交流子网、直流子网的实际传输有功功率；Qac，d为 交 流 子 网 的 实 际 传 输 无 功 功 率；fac，max、fac，min分别为交流子网允许的最大、最小频率；Uac，max、Uac，min分别为交流子网允许的最大、最小电压；Pac，dmax、Pac，dmin分别为交流子网允许的最大、最小传输有功功率；k为直流子网的P-U下垂系数；Udc，max、Udc，min分别为直流子网允许的最大、最小电压；Pdc，dmax、Pdc，dmin分别为直流子网允许的最大、最小传输有功功率；Qac，dmax、Qac，dmin分别为交流子网允许的最大、最小传输无功功率。根据交流子网和直流子网的功率相等，对应交流侧的机械-电磁功率与直流虚拟电容功率相等［14］，可得：

式中：Cvir为虚拟电容，表征了母线电压的维持能力；SIC为ILC 的额定容量；TJ为虚拟惯性时间常数，表征了ILC 的调频支撑能力。对式（2）两边求积分，可得：

式中：kh为直流侧和交流侧的耦合系数；Udc，n为直流侧额定电压；fn为交流侧额定频率。式（4）为ILC 的混合下垂方程，直流侧电压平方差与交流侧频率成下垂关系，因此本文中用电压平方差代替文献［13］中的电压差来计算电压偏差，假设功率由直流侧流向交流侧为有功功率的正方向，为了避免频繁切换，设置死区为0.02 p.u.，当电压和频率变化在死区范围内时，传输的有功功率Pdc-ref=0，无功功率通过UQ下垂控制。

1.2 优先驱动的ILC控制

定义子网偏差系数ηpu为：

式中：fpu为归一化交流频率偏差系数；U2dc，pu为归一化直流电压平方偏差系数。当子网有不同的优先级时，得到传输功率是研究重点。假设子网i为直流子网，子网j为交流子网，PILC，ij为子网i向子网j传输的有功功率，ωi、ωj分别为子网i、j的优先级系数，ηpu，i、ηpu，j分别为子网i、j的偏差系数，表述子网i、j的过负荷或轻负荷状态。ωi（ωj）越小，ηpu，i（ηpu，j）越大，即子网i（j）的偏差系数越高。ILC 传输功率的计算是整个控制的重点。

本文建立的优化模型如下［13］：

式中：J为目标函数值；Pnd，i、Pnd，j分别为最大功率跟踪控制下子网i、j的不可调度功率；Pload，i、Pload，j分别为子网i、j的实际负荷需求功率；Pun为系统中突变的负荷功率或电源的不确定功率。

由式（6）可知，J是关于ηpu，i(ηpu，j)的二次函数且导数为正，因此最优问题是凸优化，存在唯一的最小值。本文仅研究ILC 的功率传输问题，所以忽略子网之间的线路损耗。对于有条件约束的函数最优化问题，可采用拉格朗日乘数法进行求解，将有条件函数的极值问题转换成无条件函数的极值问题，通过引入一个未知的乘子λ，构造拉格朗日函数L(ηpu，λ)如式（8）所示。

再求其一阶偏导数的解，即为最优解，如式（9）所示。

当微电网系统中子网发生负荷或微元功率突变时，交流频率或直流电压达到阈值，ILC 与各子网有物理连接，根据式（9）计算得到ηpu，i(ηpu，j)，因此子网i向子网j传输的有功功率参考值P可根据式（10）得到。

式中：kp、ki分别为有功功率比例-积分控制的比例、积分系数。由式（10）可知，当子网i和子网j的优先级系数、最大传输有功功率已知时，可直接求出子网i和子网j之间的ILC 传输有功功率。当不考虑优先级时，每个子网的下垂系数相等。当优先级系数不相等，假设图1 中子网的优先级系数ωi∶ωj= 3∶1 时，如果子网的最大传输功率相等，则将其代入式（9）可得ηpu，i∶ηpu，j= 1∶3，较大的优先级系数表明频率或电压偏差更小，较小的优先级系数表明电压或频率偏差更大。本文所提ILC控制框图如图2所示。图中：Q为从子网i向子网j传输的无功功率参考值；i0为ILC 的输出电流，其谐波分量的提取方法可参考文献［7］；U0为ILC 的输出电压；iL为ILC 的电感电流；ih为谐波电流；ihc为谐波补偿电流；Rm为负荷等效电阻；ωf、Uref分别为基波角频率、基波参考电压；Em为相电压幅值；ST为谐波视在功率估算值；GU(s)为电压控制环的传递函数，采用准比例谐振控制器；GI(s)为电流控制环的传递函数；Gc(s)为谐波电流前馈传递函数；kc为谐波阻抗重塑因子；PWM 为脉宽调制信号。

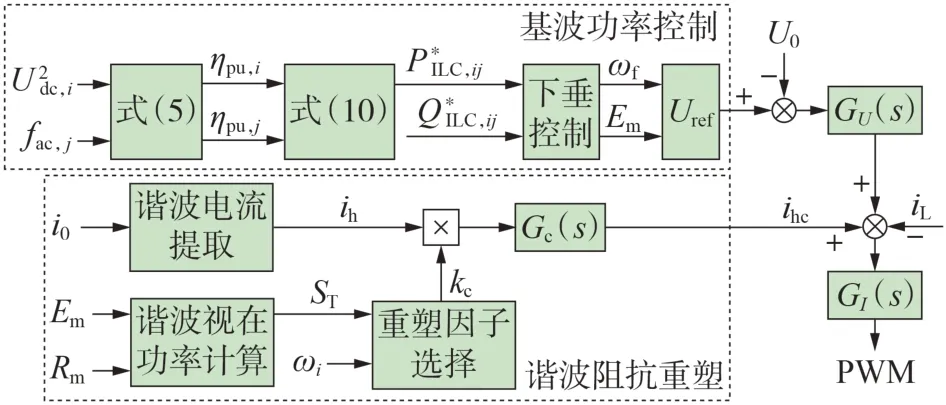
图2 ILC控制框图Fig.2 Control block diagram of ILC

2 制氢负荷建模与谐波功率估计

2.1 电解槽负荷建模

水电解槽系统包括功率转换系统、PEM电解槽、氢气储存罐、温控设备、补水设备等，为了简化所建立的电解槽模型，本文只考虑电解槽的电气模型，不考虑热模型。

根据文献［15］中电解槽的伏安特性试验结果，电解槽的主要能耗为热电阻损失，电解槽的电解总电压由开路电压Vocv、活化过电势Vact、扩散过电势Voh和欧姆过电势Vohm组成，因为扩散过电势的影响较小，故本文不予考虑。不同温度和压力下的开路电压Vocv可根据式（11）所示能斯特方程计算［15］。

式中：R为通用气体常数，取值为8.314 J／（mol·K）；F为法拉第常数，取值为96 458 C／mol；T为电解温度；z为电解反应过程中参与的摩尔电子数；αm（m∈{H2，H2O，O2}）为物质m的活度，对于理想气体，αm=Pm/P0（Pm为物质m的分压，P0为大气压），αH2O=1；考虑电解过程的热量损失，标准条件下的开路电压Vocv0由经验公式Vocv0=1.229-0.09(T-298)计算得到。

活化过电势Vact是由电化学活化过程中产生的损失造成的，用电化学动力过程中的巴-伏方程描述［16］，如式（12）所示。

式中：Ta、Tc分别为阳极、阴极的反应温度，不考虑热模型时，为电解温度；αa、αc分别为阳极、阴极的电荷转移系数；g为电流密度；g0，a、g0，c分别为阳极、阴极的交换电流密度。

欧姆过电势Vohm中膜电阻所占比例最高，当忽略其他电阻时，Vohm可表示为：

式中：δm为膜的厚度；σm为膜的电阻率，与电解温度T和含水量γ有关，可由经验公式式（14）得到。

根据上述公式，可得到电解槽负荷的外电气特性曲线，如附录A 图A1 和图A2 所示。当达到一定的电解电压后，电解槽可近似为恒电阻特性。

根据水电解的整体反应，制取1 mol的氢气需要2 mol 电子，2 mol 电子的电荷量为2×96 485 C，将该电荷量转化为电量，为2×96 485/3 600 A·h。标准工况下，1 mol 氢气的体积为22.4 L，即0.002 24 m3，所以制取1 m3氢气需要的电量为2 393 A·h。根据设计电流密度和有效电解区域直径计算电解槽电流。以某公司的实际2 kW 电解槽数据为例，估算膜电极数量的过程如下。

1）假设电流密度为8 000 A／m2，产氢速率为0.5 m3／h，产氧速率为0.25 m3／h，设计工作温度为80 ℃，工作压力为3 MPa，膜电极喷涂区域的有效面积为6 cm×6 cm，小室电压为1.75 V。

2）根据电流密度及有效电解区域直径计算得到电解槽的电解电流为8 000×36×10-4=28.8 （A）。

3）根据法拉第电流定义，在电极界面上发生化学变化物质的质量与通入的电量成正比，即电解槽的产氢速率与电解总电流成正比［17］。由上述计算可知，制取1 m3氢气的耗电量为2 393 A·h，则产氢速率为0.5 m3／h 时的耗电量为1 196.5 A·h，电解槽的小室数量为1 196.5/28.8≈42。则电解槽的电解电压为1.75×42=73.5 （V）。复合总功率为73.5×28.8=2 116.8 （W）。

2.2 功率转换单元建模与谐波功率估计

电解槽通过功率转换系统与微电网连接。为了模拟谐波功率最大的情况，本文中的AC／DC 转换采用不可控整流器，DC／DC采用Buck降压电路，通过改变Buck 电路的输出电解电流来改变电解槽功率，等效电路如附录A 图A3 所示。文献［18］针对二极管不控整流负荷，以d轴定位到相电压矢量的正方向上，根据电源相电压和负荷电阻计算得到d轴和q轴谐波电流最大值Ihdmax、Ihqmax以及谐波电流有效值Ihd、Ihq，分别如式（15）和式（16）所示。

定义d轴电流的自相关波形系数kd为d轴负荷电流的有效值与最大值之比，q轴电流的自相关波形系数kq为q轴负荷电流的有效值与最大值之比，电流的互相关波形系数为d轴负荷电流最大值与q轴负荷电流最大值之比。由式（15）和式（16）可得，谐波电流的自相关波形系数kd= 0.477 4、kq= 0.625 3，互相关系数为0.377 1，由于d轴定位到电压矢量的正方向，q轴电压uq=0，则可得谐波视在功率估算值ST为：

式中：Ud为交流侧电压经Park 变换后的d轴分量。当Rm和Em已知时，结合式（15）—（17）可估算得到电解槽负荷的谐波视在功率，简化了传统计算谐波功率过程中大量的平方、开方运算，降低了控制器的运算负担。

3 自适应谐波功率分配策略

3.1 谐波功率分配机理

1.2 节中微电网功率协调控制仅对基波功率分配有效，加入制氢负荷后，其产生的谐波电流／功率也应合理分配给ILC 和交流子网。交流母线电压vac见式（18）。由式（18）可知，ILC 可等效为可控电压源H(s)Uref与等效输出阻抗ZILC(s)串联，其中H(s)为ILC 控制系统的等效传递函数。交流子网中的分布式电源也是电压源模式，维持交流母线电压和频率稳定，其戴维南等效形式与ILC 一致，也是Hac(s)Uac与等效阻抗Zac(s)串联，其中Hac(s)为交流子网控制系统的等效传递函数。交流母线接入的制氢非线性负荷可等效为电流源iload。交直流混合微电网的戴维南等效电路如附录A图A4所示。

由式（18）可知，交流母线电压vac由三部分组成，由于参考电压为纯正弦电压，vac畸变的主要原因为等号右侧第3 项的电流源，其系数大小决定了vac的畸变程度。交流子网微源具有“即插即用”性质，等效阻抗难以确定，通过控制ILC 谐波阻抗能够控制谐波源在ILC 支路和交流子网之间的谐波分配。当ILC 谐波阻抗小于交流子网谐波阻抗时，谐波源脉动的谐波功率会通过ILC 的耦合作用传输到直流侧，导致ILC 直流侧出现多倍频脉动；当ILC 谐波阻抗大于交流子网谐波阻抗时，脉动的谐波功率会通过交流子网变流器的耦合作用传输到交流子网微源的直流侧，导致交流子网微源的直流侧出现多倍频脉动。

3.2 基于优先级和谐波阻抗重塑的ILC多模态运行

根据图2中的ILC控制结构，当交流侧有非线性负荷时，输出电流i0由基波电流if和谐波电流ih组成。ILC 的电压电流双环控制框图如图3 所示。图中：KPWM为逆变器的等效增益，取为Udc/2；Lr为滤波电感；Rr为电感寄生电阻；C为滤波电容。

图3 ILC的电压电流双环控制框图Fig.3 Voltage and current dual-loop control block diagram of ILC

根据图3，忽略Rr的影响，将i0作为扰动量，可计算得到等效输出基波阻抗Zf和谐波阻抗Zh为：

可推导得到ILC的输出电压U0为：

由于Uref不含有谐波成分，ILC 的输出基波电压由参考电压、基波电流、基波阻抗决定，而谐波电压由谐波阻抗、谐波电流决定，相互之间没有耦合。ILC的谐波阻抗伯德图如附录A图A5所示。

为了实现谐波功率按照优先级分配，首先提取输出电流进行分频谐波处理，本文建立的模型为三相三线制，负荷对称，所以不考虑偶数次谐波的影响。如果令式（19）的分子为0，则ILC 的等效谐波阻抗为0。理论上，ILC 没有谐波阻抗，引入谐波阻抗重塑因子kc［8］，通过式（21）所示谐波电流前馈传递函数Gc(s)即可实现电流前馈补偿。

谐波阻抗重塑因子kc的取值为：

式中：SILCr为ILC 的剩余容量。当ILC 所连接交流子网的优先级系数大于直流子网的的优先级系数时，kc=1，实现全补偿，谐波阻抗为0，负荷谐波功率由直流子网提供，ILC 直流侧出现多倍频脉动，能否实现全补偿受限于ILC的剩余容量；当ILC所连接直流子网的优先级系数大于交流子网的优先级系数时，kc<0，谐波阻抗增大，负荷谐波功率由交流子网提供，ILC 的输出电流正弦且对称，直流侧不会出现多倍频脉动；当ILC 所连接直流子网的优先级系数等于交流子网的优先级系数时，kc=0，谐波电流按照初始阻抗分流，ILC 提供部分谐波功率，直流侧会出现多倍频脉动。

综上，本文提出了一种自适应虚拟谐波阻抗重塑方法，通过实时检测ILC 的剩余容量、子网优先级和谐波容量视在功率来调节重塑因子。在不过载的情况下，当ILC 所连直流子网的优先级系数大于交流子网的优先级系数时，增大虚拟阻抗，由交流子网提供谐波功率；当ILC 所连直流子网的优先级系数小于交流子网的优先级系数时，减小虚拟阻抗，由直流子网提供谐波功率；当ILC 所连直流子网的优先级系数与交流子网的优先级系数相等时，按照各自的初始阻抗分配谐波功率。

4 实验验证与分析

为了验证本文所提策略的有效性和正确性，利用Easygo 实时仿真器搭建交直流微电网系统，结构如图1 所示。主电路采用PXIe-6500 仿真板卡实现，以1 μs 步长完成实时计算。控制器采用PXI-6300控制板卡实现，模拟信号采用内部总线传输，生成的PWM 信号由外部线路返回给仿真器PXIe-6500形成闭环。ILC 控制采用1.2 节和第3 章的控制方法，直流子网和交流子网采用下垂电源模拟。以功率由直流子网向交流子网流动为正方向，PILC为从直流子网向交流子网传输时的ILC 功率，当PILC>0 时，ILC 为逆变模式，当PILC<0 时，ILC 为整流模式。由于本文仅考虑谐波影响，不考虑无功功率问题，故仅对有功功率的谐波分配进行分析。相关参数取值如附录A表A1所示。

4.1 电解槽负荷等效阻抗特性验证

为了验证所建电解槽单体模型的准确性，将模型的仿真数据与电解槽的极化曲线实测数据进行对比，如附录A 图A6 所示，其中实测数据来自文献［19］中图19的Test B。由图A6可知，仿真数据与实测数据的最大误差出现在0.3 s 时，最大相对误差Δδmax=2.6 %，未超过3 %，该结果验证了本文所建电解槽单体模型的电化学特性是准确的。

基于第2章，将42个小室串联构成2 kW 电解槽制氢负荷，由不可控整流器加DC／DC 的Buck 电路与电解槽制氢负荷相连构成实际负荷，由不可控整流器与RLC等效阻抗相连构成模拟负荷。负荷A相电流的实测、模拟结果如附录A 图A7所示。由图可知，谐波电流波形重合，表明所选用的等效RLC 阻值可用于电解槽谐波功率估计。

4.2 负荷变化时基波功率协调控制验证

以直流与交流子网的优先级系数之比ωi∶ωj= 3∶1为例分析，直流子网电压偏差标幺值与交流子网频率偏差标幺值之比ηpu，i∶ηpu，j= 1∶3，2.5 s 时直流负荷从10 kW 增加到20 kW，交流子网的水电解制氢负荷为2 kW，线性负荷为5 kW，该负荷波动下的系统动态响应结果见图4。图中：ηpu，i、ηpu，j均为标幺值。

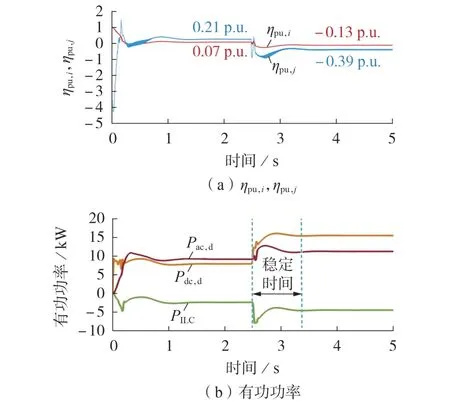
图4 负荷波动下系统的动态响应Fig.4 Dynamic response of system under load fluctuation

由图4（a）可看出，2.5 s 前ηpu，i= 0.07 p.u.，ηpu，j=0.21 p.u.，符合子网偏差系数的要求。由图4（b）可看出：2.5 s前，ILC传输的有功功率为-2.2 kW，直流、交流子网输出的有功功率分别为7.8、9.2 kW，可见直流子网的10 kW 负荷由直流子网和交流子网共同承担；2.5 s 后，ηpu，i= -0.13 p.u.，ηpu，j= -0.39 p.u.，也符合子网偏差系数的要求。ILC 传输的有功功率为-4.3 kW，直流、交流子网输出的有功功率分别为15.7、11.3 kW，可见直流子网的20 kW负荷也由直流子网和交流子网共同承担，稳定时间小于1 s。

2.5 s 时交流侧线性负荷从5 kW 增加到10 kW，水电解制氢负荷保持2 kW 不变，直流侧负荷保持10 kW 不变，该负荷波动下的系统动态响应结果如附录A 图A8 所示。由图可知：2.5 s 后实际的ηpu，i=-0.07 p.u.，ηpu，j= -0.21 p.u.，这也符合子网偏差系数的要求；交流子网的12 kW 负荷由直流子网和交流子网共同承担，稳定时间也小于1 s。

4.3 自适应谐波功率分配策略验证

当直流子网负荷为20 kW，交流侧子网为5 kW线性负荷和2 kW 水电解制氢负荷时，交流侧向直流侧提供功率，在2.5 s 时加入自适应谐波功率分配策略，由于此时电解制氢负荷功率均由交流子网承担，直流子网电压如图5（a）所示，交流子网电压如图5（b）所示。由图可知，直流电压的波动幅值小于1.5 V，ILC 输出A 相电压在2.5 s 前的总谐波畸变率（total harmonic distortion，THD）为4.17 %，2.5 s 后的THD 为4.11 %，加入自适应谐波功率分配策略前、后的THD 变化不大，这是因为此时直流子网不提供交流子网的谐波功率，kc=0。

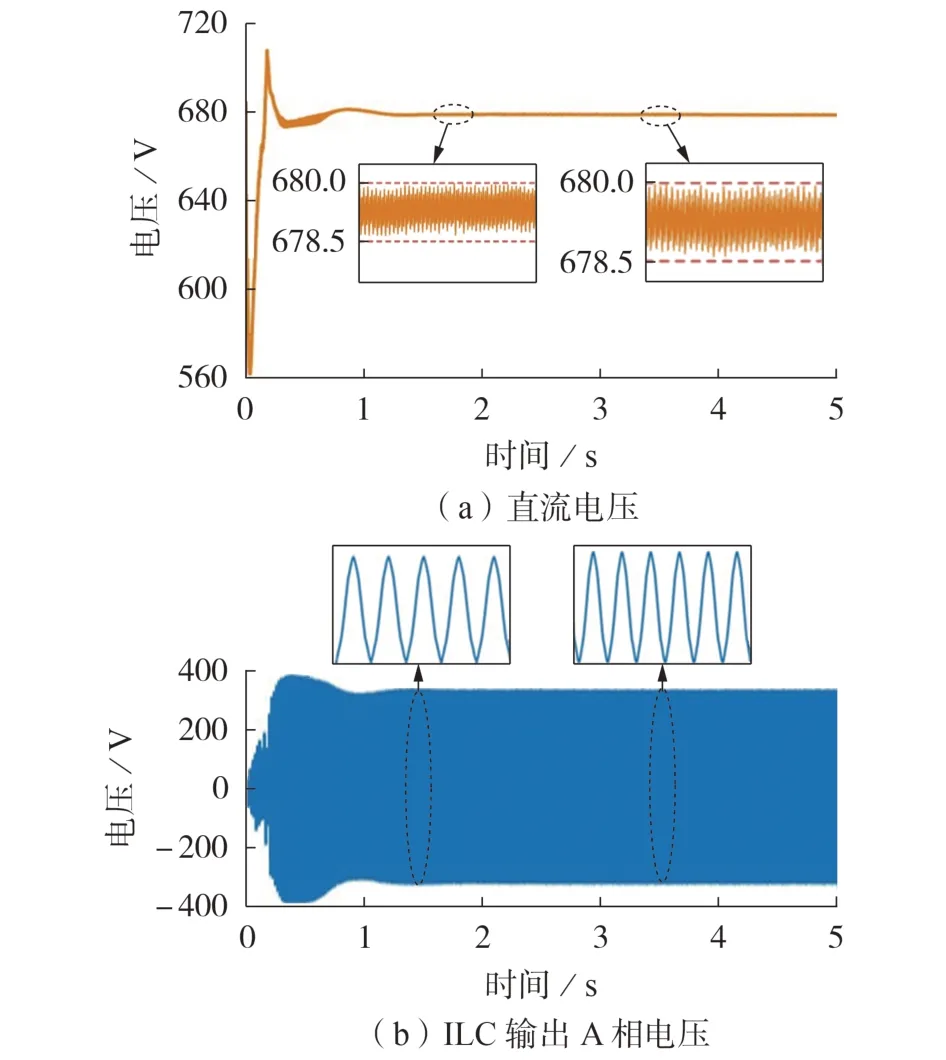
图5 加入自适应谐波功率分配策略前、后的结果对比Fig.5 Comparison of results between with and without adaptive harmonic power distribution strategy

当直流子网负荷为10 kW，交流侧线性负荷为5 kW，水电解制氢负荷为10 kW，直流子网向交流子网提供部分功率时，由于此时电解制氢负荷功率由交流子网和直流子网共同承担，kc=0，在2.5 s 时加入自适应谐波功率分配策略，kc=-5，ILC 传输的有功功率如图6 所示。由图可知，2.5 s 后，ILC 谐波阻抗增加，谐波功率由交流子网承担，直流子网电压波动减小，ILC传输有功功率的脉动功率降低。

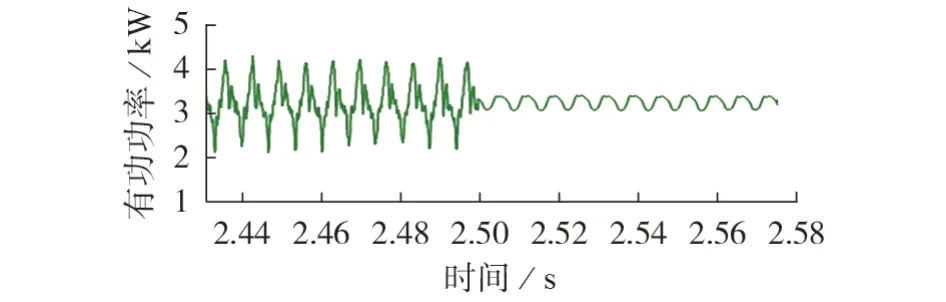
图6 加入自适应谐波功率分配策略前、后ILC传输的有功功率Fig.6 Transmission active power of ILC with and without adaptive harmonic power distribution strategy

当2.5 s 前直流子网与交流子网的优先级系数之比ωi∶ωj=1∶1，2.5 s后ωi∶ωj=1∶3，其他参数与前文相同时，交流电压曲线如图7 所示。由图可知，2.5 s后，ILC 谐波阻抗降低，谐波功率由直流子网承担，交流子网的电压THD 从10 % 降低到3.86 %，提高了高优先级子网的电压质量。

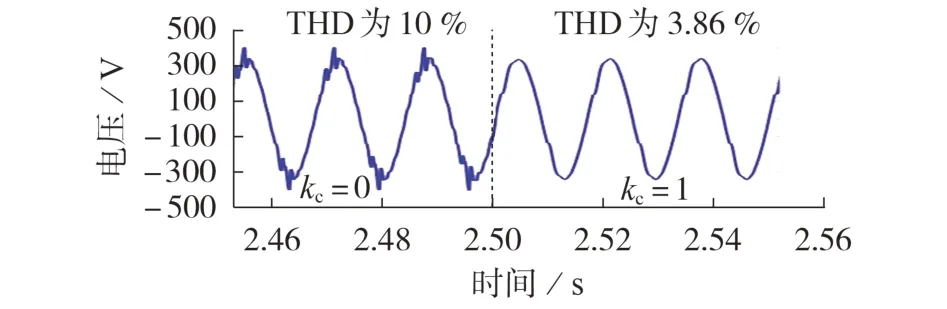
图7 交流电压曲线Fig.7 AC voltage curve

5 结论

针对交流制氢负荷接入微电网低优先级交流子网中，会导致高优先级直流子网电压出现多倍频脉动的问题，本文提出了一种考虑子网优先级系数的自适应谐波功率分配策略，并通过硬件在环实验进行验证，所得结论如下：

1）针对水电解制氢负荷，详细建立了PEM 电解槽和功率转换系统的模型，并根据实际电解槽数据估算小室数量，实验结果验证了估算值的正确性；

2）与常规的谐波功率均分不同，本文所提策略实现了在ILC 不过载的前提下，采用无须构建虚拟阻抗的方法实现了自适应、宽范围重塑ILC 谐波阻抗的目的，改善了高优先级子网的电压质量；

3）本文所提策略不需要通信获取，并计算实时的谐波功率信息，根据制氢负荷相关信息估算谐波功率，降低了计算负担。

附录见本刊网络版（http：//www.epae.cn）。