考虑线性区大小的电流互感器饱和识别方法研究

刘 义

（国家电投集团协鑫滨海发电有限公司）

0 引言

电流差动保护原理简单， 速动性好， 具有很高的灵敏度， 已被广泛用于线路及电气设备的主保护。差动保护能否可靠识别出区内故障， 主要取决于对应的电流互感器 （CT） 是否能够正确地传变故障和非故障电流 。当CT 发生铁心饱和时， 其二次电流会产生畸变， 从而影响差动保护的正确动作。

目前， 国内外学者提出了多种CT 饱和识别方案，包括时差法 、 小波变换法、 谐波比法等。其中， 应用较多的是时差法。该方法通过识别故障发生时刻与差流出现时刻是否存在时间差来区分区外和区内故障，当判别为区外故障时， 将保护闭锁一段固定时间。但是当闭锁期间发生区内故障时， 保护将延时动作。针对这一问题， 有学者提出CT 线性区开放保护的方法 ， 即在CT 进饱和时刻闭锁保护， 在CT 退饱和时刻开放保护。但是如何正确判断CT 进饱和时刻与退饱和时刻， 判别出CT 的线性传变区是实现此方法的难点。

1 CT饱和产生原理和波形特征

1.1 CT饱和产生原理

CT 的等效电路图如图1 所示， 图中Z1为CT 的一次阻抗，R2为二次电阻，L2为二次电感，R为CT 的二次负载电阻， L 为CT 的二次负载电感，Lμ为CT 的励磁电感。

CT 铁芯由铁磁材料做成， 铁芯中磁通与磁感应强度呈非线性关系。当铁芯不饱和时，Lμ的数值很大， 因此励磁电流很小， 一次电流几乎完全传变到二次侧； 当CT的一次电流增大后， 尤其一次电流中含有较大的直流分量， 铁芯开始饱和，Lμ迅速下降， 励磁电流增加 。当CT 严重饱和时， 此时二次侧电流发生明显畸变。

CT的饱和类型可以分为两类 ：

（1） 稳态饱和： 只考虑一次电流周期分量幅值的增加和互感器二次负载的改变对CT 饱和的影响， 忽略暂态非周期电流直流分量带来的影响；

（2） 暂态饱和： 只考虑短路时可能出现的暂态非周期直流分量对CT饱和的影响。因为传统电磁式CT对直流分量的传变特性较差， 直流分量无法传变， 会全部形成励磁电流， 从而造成CT 快速达到饱和状态，而且饱和程度一般很深。

1.2 CT饱和时的波性特征

CT饱和时的波形图如图2所示。

图2 CT饱和时理想与实际的二次侧电流波形

由波形图可以看到， 短路发生后， CT并没有立即进入饱和， 而是存在一个线性传变区， 在这一区间内， CT可以将一次侧电流正确传变到二次侧， 线性传变区的大小与CT 的饱和深度有关。所以当发生区外故障引起CT饱和时， 差动电流不会立刻出现， 而是与故障发生时刻存在一定的时间差， 时差法正是利用这个原理来识别区外故障的。CT 饱和后， 随着一次电流的减小， CT逐渐退出饱和， 在一次电流过零点附近同样存在一个线性传变区， 在一个周波内， 该线性区的大小与上一个线性传变区的大小相等。

2 基于线性区大小的门槛值辅助判据

2.1 CT 线性区的量化原理

由图1 的电路图可知：

在微机保护中， 由于二次负载极小， 且多为纯电阻， 同时为了简化分析， 我们不计CT 二次侧绕组的漏抗和铁芯损失， 可以得到：

化简得：

式中，

然后利用线性一阶微分方程的求解方法， 我们可以得到励磁电流与一次电流的关系式为：

而故障发生后， 一次电流通常可以表示为：

式中，Im为一次电流周期分量的幅值；a为电源电势的初始相角；φ为短路回路的阻抗角；C0为一次电流非周期分量的初始值；Ta为非周期分量衰减的时间常数。

将其代入式 （6） 可得：

由于CT 铁芯是否处于饱和状态取决于励磁电流的大小， 所以可以给励磁电流设定一个阈值， 当励磁电流的大小超过该阈值时， 判别为CT 饱和， 得到CT的饱和时刻， 再根据故障发生时刻就可以实现对线性区大小的量化。

2.2 双端输电线路线性区大小的确定

常见的双端输电线路的简化电路图如图3 所示。

图3 双端输电线路简化电路图

当双端系统T1时刻发生区外故障 （K2 点） 时， 由于该系统为线性系统， 所以可以将两个电源分开单独考虑， 然后运用叠加原理进行综合。只考虑电源ES时， 对应的简化电路图如图4 所示。

图4 只考虑ES时的等效电路图

故障前， 线路的电阻和电抗分别为RS+RL和XS+XL， 电流为Im， 线路的阻抗角为φ， 电源电势的初始相角为α； 故障发生后， 线路的电阻、 电抗、 电流和阻抗角均不发生变化， 则短路电流中的非周期分量为0， 式 （8） 可以化简为：

将相关参数代入， 同时令iμ=iN， 可以得到CT的饱和时刻T2， 此时线性区的大小为T=T2-T1。

只考虑电源ER时， 对应的简化电路图为图5所示。

故障前， 线路的电阻和电抗分别为RR+RL和XR+XL， 电流为I'm， 线路的阻抗角φ'， 电源的初始相角为α1； 故障发生后， 线路短路回路的电阻和电抗RR和XR， 电流为Im， 短路回路的阻抗角为φ， 利用公式（7） 可以计算得到非周期分量C0。

代入相关参数， 利用式 （8）， 令iμ=iN， 可以得到CT 的饱和时刻T'2， 此时线性区的大小为T'=T'2-T1。然后运用叠加原理， 可知双端系统区外故障时，CT 饱和线性区的大小为T+T'。

2.3 基于线性区大小的门槛值辅助判据

基于线性区大小的门槛值辅助判据是根据CT 饱和时的差动电流波形特征提出来的。区外故障时CT饱和引起的差流在二次电流线性传变区为零， 而区内故障时的差流呈正弦波的形状， 只有在二次电流过零点时刻才为零， 利用差动电流的这个特点， 我们可以定义一个阈值， 作为制动电流， 然后统计一个周波内大于该制动电流的点数N， 如果N>D（为与线性区大小相关的门槛值）， 则判断CT 饱和， 开放保护，否则判断CT 退出饱和， 闭锁保护。

对于正弦波来说， 我们选取第一个采样点值的0.8 倍作为制动电流的值。这样， 对于一个周波内的采样数据， 只有当差动电流采样值为零时， 才能满足差动电流小于该制动电流。门槛值D与CT 线性区的大小T 之间存在着一定的映射关系， 以一个周波取24 个采样点为例。当二次电流处于线性区时， 差流为零， 小于制动电流的采样点的点数为：

考虑一定的裕度， 选取两个点数的裕度， 门槛值选取为：

我们可以通过确定CT 的饱和时刻 （即励磁电流越限的时刻）， 同时根据故障发生时刻， 得到CT 的线性区大小T， 从而确定门槛值D的值。这样， 当时差法判别为区外故障闭锁保护时， 发生区内故障， N 值迅速变大， 超过门槛值D， 解除闭锁信号， 开放保护。

基于线性区大小的门槛值辅助判据实现流程图如图6 所示。

图6 基于线性区大小的门槛值辅助判据实现流程图

具体实现步骤为：

（1） 检测线路出现故障， 记录故障时刻T1；

（2） 获取一次侧电流数据， 根据式 （8）， 计算励磁电流；

（3） 若iµ>iN， 判断CT 饱和， 反之则为正常运行状态。其中iN是根据CT 不同精度所选取的阈值， 通常， 5P 型CT 取二次侧额定电流的5%， 10P 型取二次侧额定电流的10%。

（4） 根据CT 饱和时刻T2， 确定线性区得大小T；

（5） 根据线性区大小， 确定门槛值D；

（6） 统计一个周波内大于制动电流的点数N， 若N>D， 开放保护， 否则闭锁保护。

3 仿真实验

3.1 仿真条件

利用电磁暂态程序PSCAD/EMTDC 建立仿真模型， 如图7 所示。其中， 线路AB 两端分别采用电子式CT 和电磁式CT， K1 代表区内故障， K2 代表区外故障， 电压等级为500kⅤ， 两个电源初始相角相差10°。系 统 阻 抗ZS1= 1.05 +j22.18，ZS0=j28.09，ZR1= 1.06 +j24.92，ZR0=j35.47。输 电 线 路 参 数见表1。

表1 输电线路分布参数

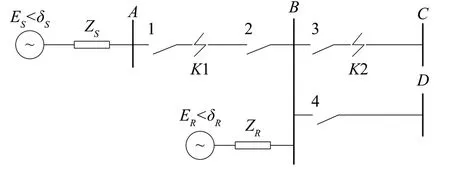
图7 输电线路仿真模型图

选取AB 线路长度为160km， BC 线路长度为40km， BD 线路长度为70km， 在线路各种短路故障中， 以单相接地故障和三相短路故障对电网造成的冲击最大。所以在下面的仿真计算中选取这两种短路故障情况进行分析。

3.2 仿真验证

（1） 单相接地故障

在上一节建立的仿真模型基础上， 设置K2 点处在0.2s 时发生短路故障， 0.4s 时出现K1 处的区外转区内故障。根据PSCAD 仿真中的到的数据， 运用结合新饱和识别方法的保护闭锁与开放方案， 可以计算出第一个线性区为4.8ms， 从而确定门槛值为10。运用仿真系统验证门槛值为10 的正确性， 图8 表示差动电流波形图， 图9 表示N值变化图。

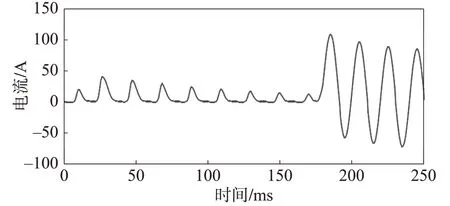
图8 差动电流波形图

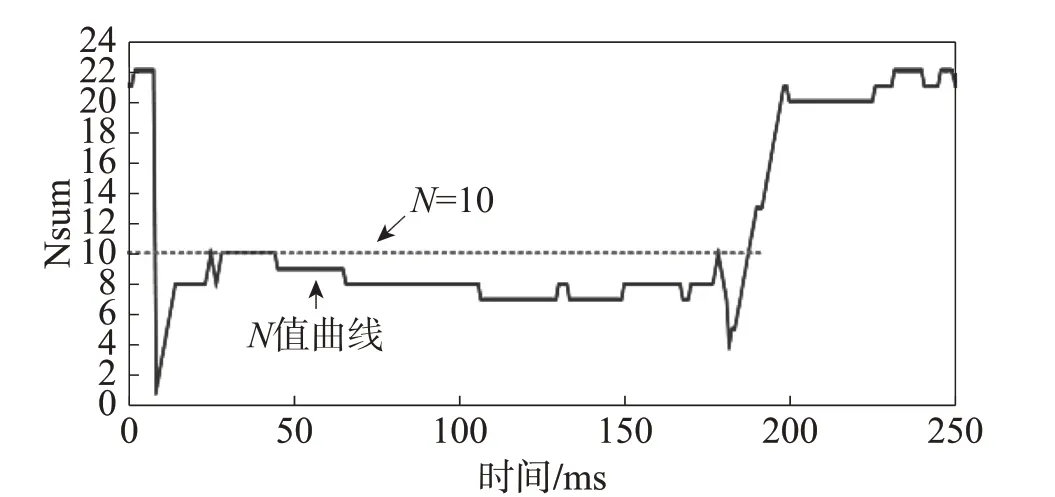
图9 N值变化曲线图

从图中可以看出， 发生区外故障时，N值曲线的最大值不超过10， 此时保护闭锁， 转区内故障后，N值迅速增大， 保护开放。

（2） 三相短路故障

根据PSCAD 仿真中的到的数据， 运用结合新饱和识别方法的保护闭锁与开放方案， 可以计算出第一个线性区为3.6ms， 从而确定门槛值为12。运用仿真系统验证门槛值为12 的正确性， 图10 表示差动电流波形图， 图11表示N值变化图。

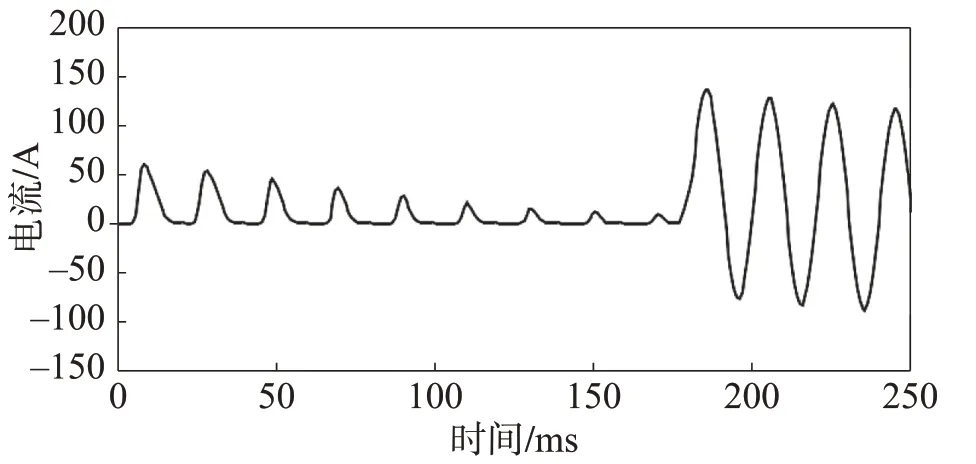
图10 差动电流波形图

图11 N值变化曲线图

从图中可以看出， 发生区外故障时，N值曲线的最大值不超过12， 此时保护闭锁； 转区内故障后，N值迅速增大， 保护开放。

4 结束语

本文针对时差法在区外故障时将保护闭锁一段固定时间， 当闭锁期间发生区内故障时保护延时动作的问题， 通过对CT线性传变区进行量化， 同时结合时差法， 提出基于线性区大小的门槛值辅助判据。当发生区外故障时， 首先由时差法识别出CT 饱和， 闭锁保护， 同时在闭锁期间， 利用辅助判据对系统进行监测，如果发生区外转区内故障， 大于制动电流的采样点数将越过门槛值， 从而解除闭锁信号， 开放保护。仿真结果表明了在区外转区内故障时该辅助判据的正确性。