基于高渗透率能源的新型储能系统配电网规划方法研究

王灵龙 张 璐

（国网重庆市电力公司永川供电分公司）

0 引言

近年来， 煤炭、 石油和天然气资源的供需以及全球碳排放持续上升， 导致不可再生能源消耗和环境污染问题日益突出[1-2］。分布式新能源发电以其安装方便、 环境友好、 利用率高等优点得到了迅速的发展[4］。关于新能源大规模接入分销网络的问题已经出现。光伏发电是间歇性的、 不稳定的和连续的， 它影响电网的安全和经济运行[5］。例如， 系统的双向潮流和接入点的电压限制不能解释本地消耗， 从而增加了系统的网络损耗。储能系统 （ESS） 的高效充放电和负荷波动的快速调节特性可以有效缓解新能源输出和负荷需求之间的时间匹配问题， 并形成对新能源的时空补充。因此， 在ESS 规则的支持下， 基于新能源连接大规模电网连接规划的概念应运而生。

1 规划方法分析

新型储能系统 （如钠离子电池、 液流电池、 固态电池等） 具有高效、 长寿命、 环保等优点， 在配电网中得到了越来越广泛的应用。高渗透率能源 （如太阳能、 风能等） 可以通过储能系统储存起来， 在风光不足时供给用电设备， 实现能源的平衡和优化利用。

基于高渗透率能源的新型储能系统配电网规划方法， 需要考虑以下几个方面： 确定储能系统的规模和数量， 首先需要确定储能系统的规模和数量， 根据可再生能源的产生量和负载需求量等因素， 确保储能系统的容量能够满足需求， 并在电网中实现有效的分布和管理。确定储能系统的类型， 不同类型的储能系统有着不同的特点和适用范围， 需要根据具体情况选择合适的储能技术， 如流动电池适用于长时间放电、 频繁充放电情况， 钠离子电池则适用于长期静态放电。优化储能系统的运行策略， 储能系统的运行策略可以通过预测、 控制和优化来实现， 在实时监测环境和电网状态的基础上， 实现储能的充放电、 联网和自主控制。考虑储能系统与其他设施的相互影响， 储能系统与其他设施 （如发电设备、 传输设施等） 相互协作， 在实现高效能源利用的同时， 还需要考虑不同设施之间的相互影响和协同作用。

总之， 基于高渗透率能源的新型储能系统配电网规划方法需要综合考虑技术、 经济和环境等多个方面的因素， 以实现可持续、 高效、 灵活和可靠的能源供应和利用。

2 考虑需求响应的配电网运行模型

2.1 目标函数建立

规划策略是在不影响用户正常生产活动， 以及风能和太阳能总消耗的情况下， 规划储能输出和可转移负荷输出， 从而实现配电网运营的经济性， 这本质上是一个多目标的最佳化问题。在本文中， 目标是最小化配电系统的总运营成本F。

式中，Cm为各单位的经营成本， 按公式 （2） 计算，CDR是需求响应成本， 按方程 （3） 计算，CESS.loss是指储能电池的损耗成本， 按方程 （4） 计算，CEP，Cpl分别是从上级电网购电成本和网损成本， 分别按方程（5） 和 （6） 计算。

cm,loss为机组运行的单位成本系数 （RMB/MW）；Pi为第i台机组的发电功率 （MW）；T为周期；I为机组的数量。

式中，C1为单位功率下可转移负荷 （RMB/MW），PTL,i(t) 是在时间t时第一个可转移负载的功率，NTL表示可转移负荷的数量。

CESS.loss单位功率损耗是指蓄电池的单位功率损耗成本， RMB/MW；PESS.i(t) 是指第一节蓄能电池在t时的充放电功率；NESS表示蓄能量的数量。

式中，p(t) 为时间t的电价，PPL(t) 为时间的净负荷功率。

closs为网络损耗的单位成本系数；Ik为在第k支路中流动的电流 （第一个节点是i， 最后一个节点为j），kA；rk为在第k支路中流动的电阻值。

2.2 模型求解方法

在DNOP 模型中， 等式约束即潮流约束是非线性的非凸约束， 因此很难求解， 需要处理目标函数和约束。本文所采用的解法是二阶锥规划 （SOCP）， 其标准形式可写为

式中，x是一个变量，x∈RN； b， c 是系数常数，b∈RM，c∈RN，AM×N∈R； K 表示二阶锥体或旋转的二阶锥体， 它们分别在方程 （8） 和 （9） 中显示， SOCP本质上是一个规划问题， 其解是最优的， 计算是非常有效的。使用仿真软件提供的复合求解器可以获得更好的结果。

在第2.1 节中， 系统总运行费用F 中的网损费用Cpl是一个需要线性化的二次函数。定义如下：

式 （6） 被转换成

然后， 对原始的功率流约束进行以下SOCP处理

经过上述线性化处理后， 本文建立的带源网络的储配电网运行规划模型可以看作是一个二阶锥规划问题。通过使用函数计算创建实数决策变量， 然后添加各种约束， 配置参数以设置求解器。最后， 对模型进行了求解， 该方法可以在较短的时间内得到最优解。

2.3 控制策略分析

式 （13） 给出了ΔP低压配电网的PⅤ与负荷之间的功率关系。

式中， ΔU是设定电压和实际电压之间的差， Ⅰ是设定电流和实际电流之间的差，U∗和I∗分别是设定电压和电流。

对于电池1和电池2， 它们的输出功率P1和P2与它们的SOC（充电状态），SOC1和SOC2相关， 如方程 （14） 所示。

将上述方程结合起来， 就可以得到方程 （15）

以电池1为例， 方程式 （15） 可以写成式 （16）

然后， 规划的控制策略可以写成方程式 （8）

这里C0是初始下垂系数。如式 （17） 所示， 规划控制是基于电池SOC建立新的系数， 可以更好地避免过充或过放电的电池。这是因为电池的SOC 是剩余的电池电源。它在电池控制策略中起着决定性的作用， 因为当电池SOC 过低时， 需要充分考虑尽可能少的充放电， 所以以电池SOC作为指示器非常合适的。

图1 显示了本文中的控制框图。如图1 所示，我们可以得到式（18）

式 中，G1（s） 是 传 递 函 数，G2（s） 是 输 出 功率闭环跟踪传递函数， 如式（19） 所示，Z0（s） 是变换器的等效输出阻抗。

式中， Gdroop 是动态下垂系数， 需要充分考虑方程 （18） 的稳定性， 可以得到方程（20）

根 据 式 （20） 和 分 析， 由 于 （SOC1/SOC2）n的存在，n的值大大影响了系统的稳定性， 并且通过计算知道它的值被推荐为1-5 以保持系统的稳定性。此外， 如方程（20） 所示， 当在合理范围内增加n的值时， 它可以大大提高电池单元1 （SOC1）和 电 池 单 元2 （SOC2） 的 收 敛 速 率， 电 池 单 元 吸收或释放功率的速率， 这可以进一步提高我们提出的策略的性能。

与传统的弧垂控制策略相比， 由于电池SOC更能代表剩余电池的功率控制， 规划了指标， 用电池SOC 代替电池电压作为参数， 可以更好地防止电池组过充过放， 保证电池组的运行安全。此外， 我 们 还 提 出 了 （SOC1/SOC2）n控 制， 这 意 味着如果电池组中的SOC 过于不同， 运用增加n来加速包中所有单元SOC 的一致性， 这比传统的弧垂控制策略具有更好的性能。

3 实例分析

3.1 模型建立

利用图2 所示的ⅠEEE33 辐射系统来验证本文建立的模型， 包括参考电压UB=12.66kⅤ和功率参考值SB=100MⅤA。该系统的网络参数依据之前研究， 配电网络包括一个风力发电机组 （WT） 、 一个光伏发电机组 （PⅤ） 、 五个可转移负荷（TL） 、三个可中断负荷 （ⅠL） 和两个储能系统 （ESS） 。规定电压 （额定值） 不得低于0.95 或高于1.05；支路电流上限为20kA； 上级电网购电的最大有功功率和无功功率不得高于5MW。最大无功功率不能大于3Mvar 或小于-1Mvar。节点2 的发电机输出功率不能超过1MW； 第一个ESS 的容量上限设为3MⅤA， 下限设为0.18MⅤA， 充放电功率不能高于0.4MW； 第二个ESS 的容量上限设为3MⅤA， 下限设为0.1MⅤA， 充放电功率不能高于0.3MW； 充电效率设为0.9， 放电效率设为1。运行周期T 的总数被设置为24。本文2.1 节中目标函数F 的参数设置如表1 所示。通过SOCP 和Matlab 中的复形求解器， 直接解决了该实例的操作规划问题。

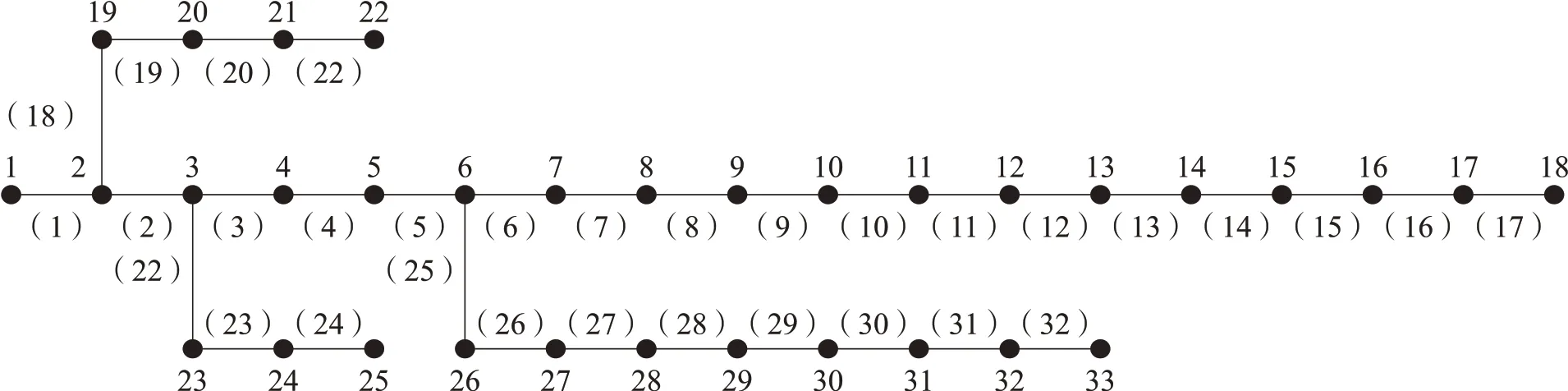
图2 IEEE33节点径向配电网

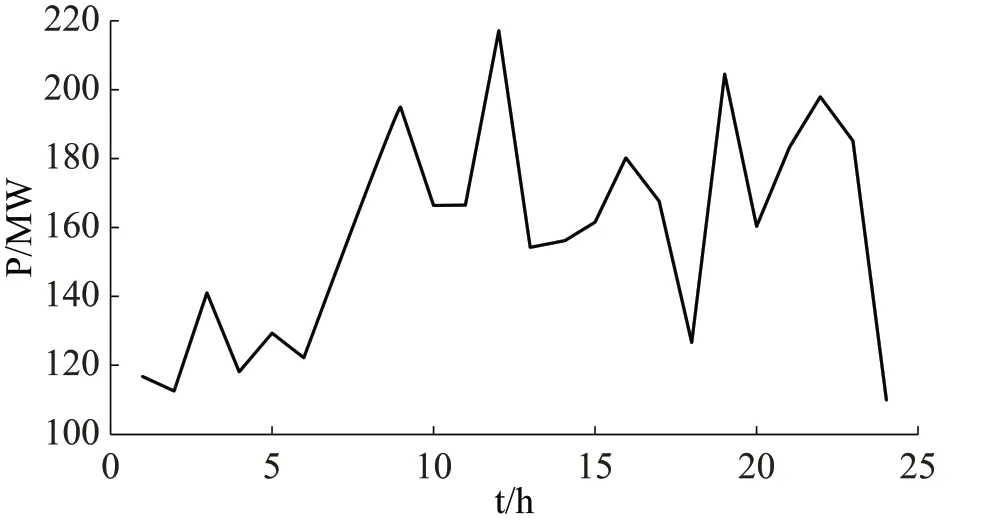
图3 总负荷曲线

在特定区域和总负荷曲线中， 每15min 选择WT 和PⅤ输出的每日时间序列数据， 每年365d。每个时刻的电价数据如图4 所示。WT 连接到17 个节点， PⅤ 连接到32 个节点， 发电机连接到2 个节点， ESS 访问节点设置为15 和23， TL 访问节点设置为5， 7， 13， 14 和20， ⅠL 访 问 节 点 设 置 为7， 13和19。

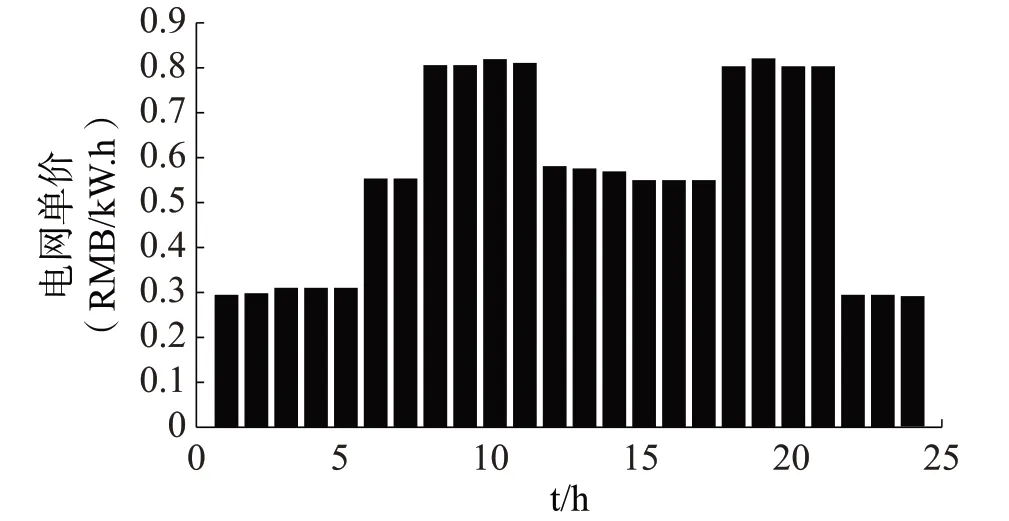
图4 购电价格

风力涡轮机具有以下输出特性：

（1） 全年产量变化很大。夏秋季风速越小， 风机产量越小。当春冬季风速较大时， 风机的输出量也较大；

（2） 光伏发电机组的输出在一天内变化不规则， 具有随机性和波动性， 光伏发电机组具有以下输出特性：

（1） 光伏产量具有明显的周期性， 呈现先增加后减少的趋势；

（2） 随机性、 PⅤ波动性明显， 最大值不确定。

对图中每四个矩的平均评价可以得到24h 的聚类结果。分别对这两种情景进行分析： 情景1： 光伏输出高达76 兆瓦， WT 输出小而稳定， 表明这一天典型的是晴天和无风； 情景2： 光伏和WT 输出非常低， 表明这个典型的一天是多云和多风的。

在两个场景中进行操作规划后的ESS 输出如图5 所示。

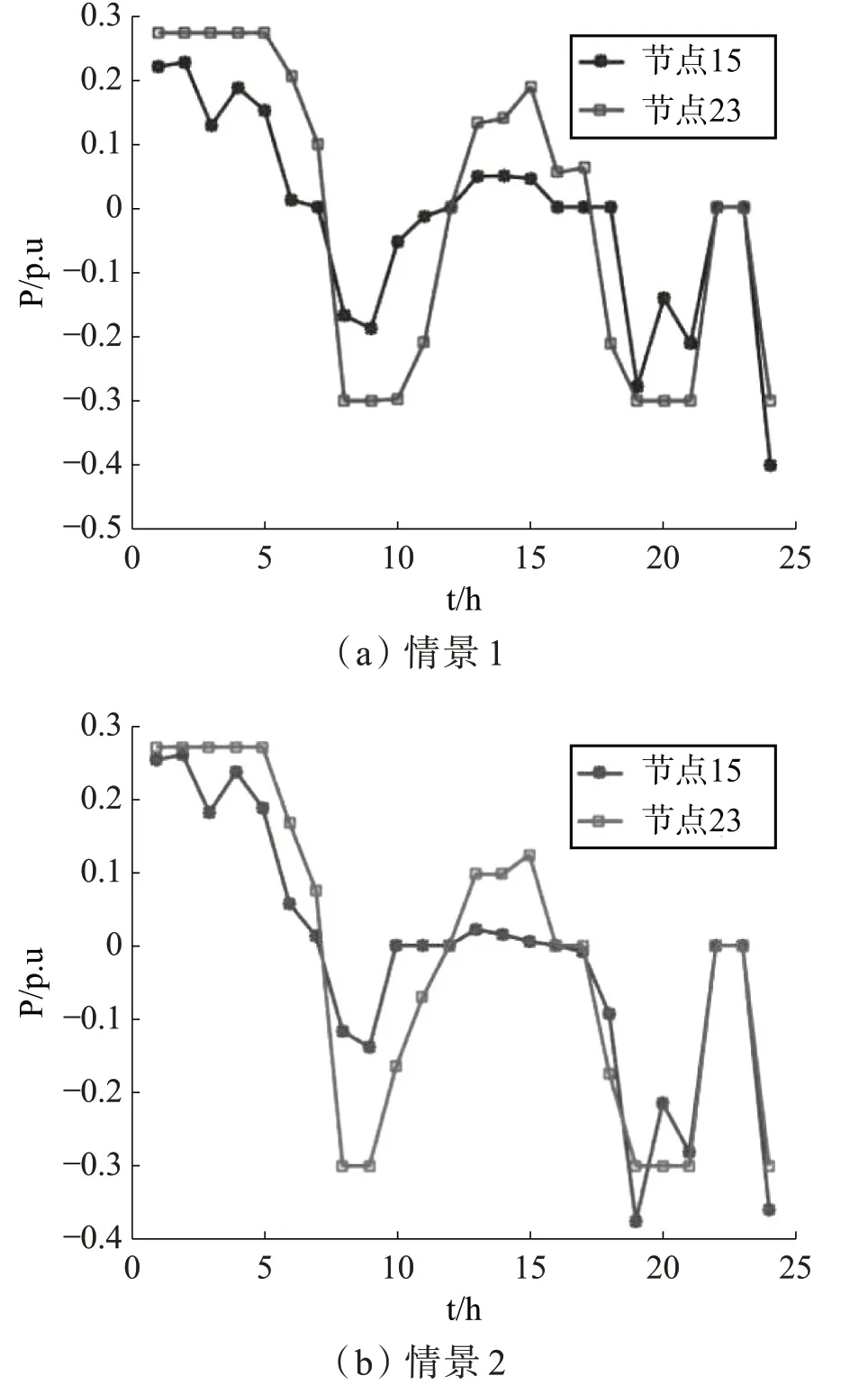
图5 两情景下ESS 输出波形

在两个场景中进行操作规划后的TL 输出如图6所示。

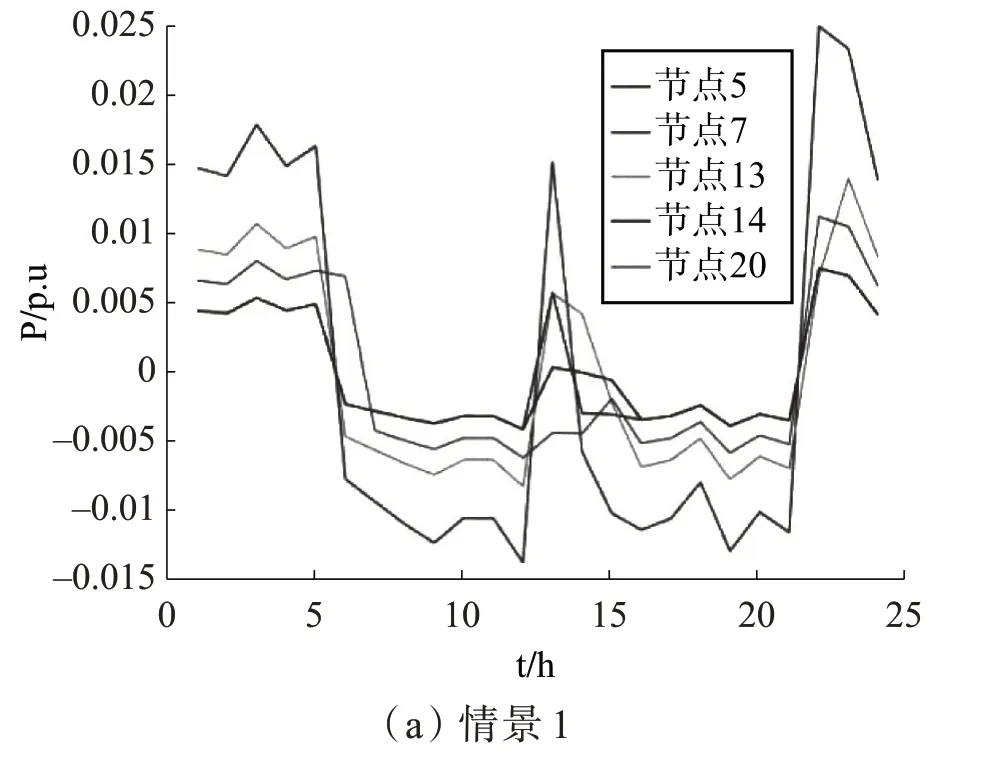
图6 两情景下TL输出波形

4 结束语

风力发电和太阳能发电机组配电网运行规划方法的研究对于整个电力系统的管理和运行具有重要意义， 可以提高系统的安全性和稳定性。本文建立了DNOP 模型， 并采用二阶锥方法求解该模型。基于ⅠEEE33总线系统验证了该方法的有效性。结论如下：

（1） 将全年365d 的小波和光伏输出量进行聚类和分割， 并将其聚类为典型场景， 得到各场景的景观聚类中心， 在后续规划过程中基本能够覆盖配电系统的年运行特征；

（2） 在建立DNOP 模型时， 综合考虑了源网络的负荷存储问题， 以单位运行成本、 需求响应成本和网络损耗成本为目标函数， 综合考虑了潮流约束、 需求响应约束和储能装置约束等条件。更符合配电网实际运行情况， 指标改善程度明显；

利用二阶锥方法和复数求解器的计算结果表明，该方法可以在总吸收风能和光能的基础上， 得到各典型场景的最低运行成本， 从而保证电网系统高效运行。