双耦合谐振子Fano共振特性的实验设计与研究
翟立朋,刘 悠*,程 琳,常凯歌,张俊武
(1.西安交通大学 物理学院 大学物理国家级实验教学示范中心,陕西 西安 710049;2.西安工程大学 理学院,陕西 西安 710048)
Fano共振最早是在1961年由意大利物理学家Ugo Fano在研究惰性气体的吸收特性时发现并解释的一种反对称共振现象[1],是因为气体分子系统中分离态能级与连续态能带进行量子干涉而产生的一种特殊的共振现象。随着人们对Fano共振研究的深入,这种特殊的共振状态已经被广泛应用在纳米超材料[2]、波导微腔[3]、石墨烯[4]、光子晶体[5]、电磁诱导[6]等前沿热点领域。
Fano共振与传统共振现象最重要的区别在于其共振谱线呈反对称分布。传统共振认为系统在做受迫振动时,当受迫频率与自身的固有频率相等时,系统做受迫振动的振幅最大,受迫频率与固有频率的差值越大,受迫振动的振幅单调减小,这种共振谱线称为洛伦兹线型,这在大学物理[7-8]和大学物理实验[9-13]课程中有比较系统地体现。Fano共振在共振点附近不仅出现了振动增强还出现了振动减弱的现象,所以构成了一种特殊的反对称线型。
Fano共振在大学物理和物理实验[14-16]中也有了初步的探索和应用。本文使用传统的谐振子模型,系统地解释Fano共振现象产生的动力学机理,详细阐述了Fano共振特性在大学物理实验教学中的设计与应用,设计并研究了一种既包含了传统共振也包含Fano共振的物理实验仪器,以期提高物理实验课程内容的高阶性、综合性和创新性。
1 Fano共振的动力学原理

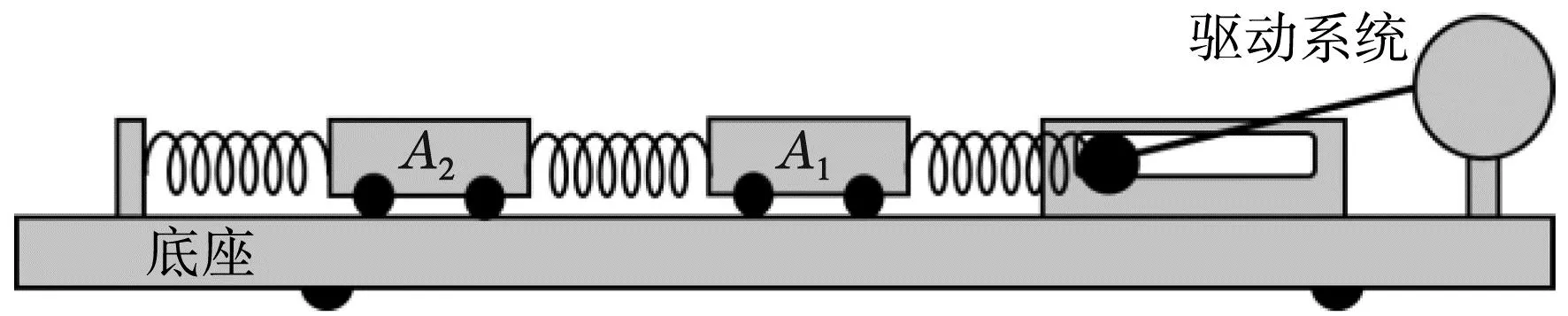
图1 双耦合谐振子共振实验仪结构图
为了更清晰的进行双耦合谐振子模型的动力学分析,将图1所示的仪器结构图转化为如图2所示的受力模型图,上下两个模型分别表示振子处于平衡状态和非平衡状态时的受力情况,其中x为弹簧的原长,而x0、x1、x2表示的是驱动振子、振子A1、振子A2的位移,m1、m2为两个振子的质量。
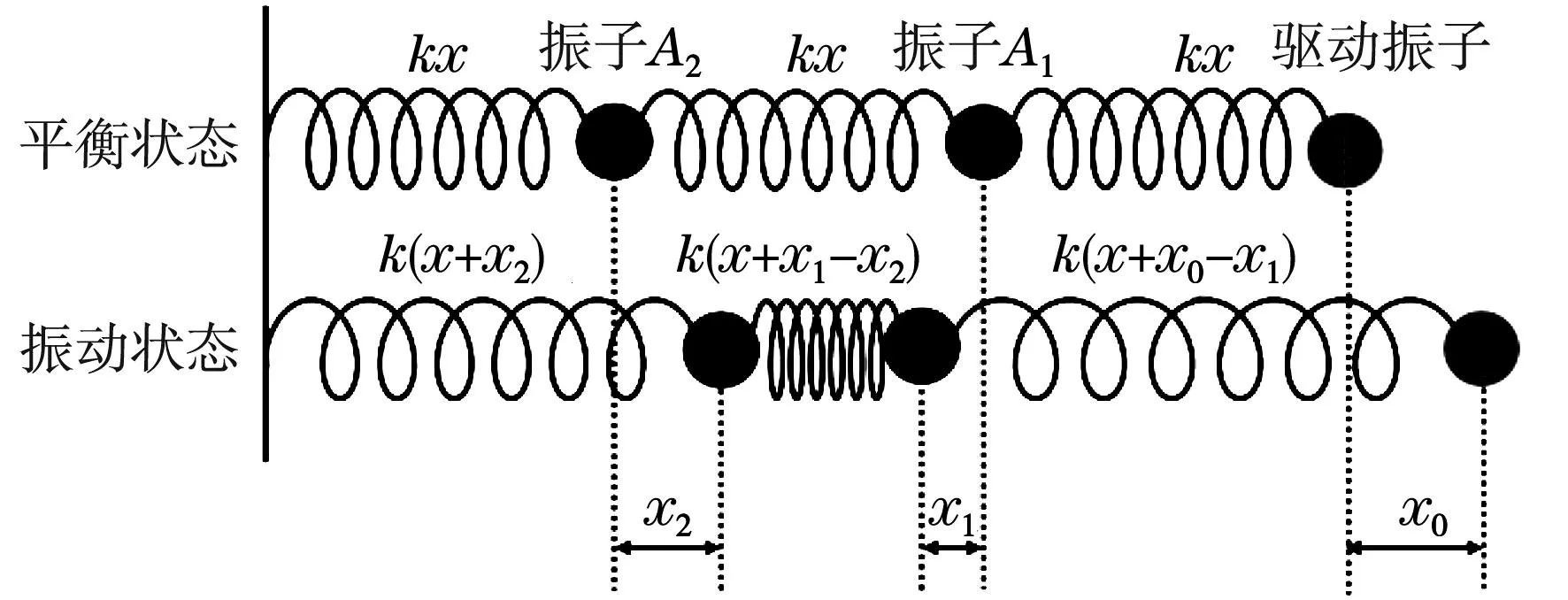
图2 双耦合谐振子共振实验受力模型图
振子A1、A2的动力学方程可表示为
(1)
(2)
将上式整理可以得到:
驱动振子受驱动力的控制做频率特定的简谐振动,可表示为
x0=A0eiωt。
振子A1、A2做受迫振动,在受迫振动稳定以后做频率与驱动频率一样的简写振动,则x1和x2解的形式可表示为
x1=A1(ω)eiωt,
(3)
x2=A2(ω)eiωt。
(4)
将(3)(4)解的形式代入到(1)、(2)动力学方程中,待定系数以后可以得到:
(5)
(6)
从(5)、(6)关于振动的表达式可以看出,当满足:
2k+iμω-m1ω2=0 ,
(7)
2k+iμω-m2ω2=0 ,
(8)
A1(ω)和A2(ω)的分母都为最小值,即振幅强度最大,可以出现共振峰。当满足式(8)时,A1(ω)的分子为零,此时共振的最大值和最小值会出现状态叠加,量子物理中解释为暗模状态和亮模状态的叠加,即Fano共振现象。
A1(ω)和A2(ω)中不仅包含了振子的振幅信息还包含了振动的相位信息,所以还可以将其表示为
A1(ω)=|A1(ω)|·eiφ1(ω),
(9)
A2(ω)=|A2(ω)|·eiφ2(ω)。
(10)
结合欧拉公式可以得到:
(11)
(12)
其中imag和real分别表示取虚部和取实部运算。对于两个振子的相位差,可以使用(9)(10)直接做差,也可以设:
Δφ=φ1(ω)-φ2(ω) ,
由欧拉公式,可以得到:
ei(φ1-φ2)=eiΔφ=cosΔφ+isinΔφ,
将(9)(10)两式相除得到:
对应到实部和虚部:
整合以后可以得到:
则相位差Δφ可表示为
(13)
这样即从理论上得到了双耦合谐振系统的振幅和相位差。
图3所示的(a)、(b)分别展示了该系统的幅频与相频特性。从幅频特性上可以看到每个振子都有两个共振峰,两个振子的自由振荡频率ω1和ω2处分别对应式(7)、(8)计算得到的共振频率,这与常规的共振特性是一致的。但振子A1在ω2附近会出现一个强度为零的谷,导致该处的幅频曲线呈反对称分布,即为Fano共振现象。

ω/(rad·s-1)(a)


ω/(rad·s-1)(a)
2 双耦合谐振子共振仪设计与测量方法
2.1 双耦合谐振子共振仪设计
按照如图1所示的结构,本文设计了如图5所示的双耦合谐振子共振仪。共振仪主要包括信号源、驱动电机、驱动振子、振子A1、振子A2五个部分。

图5 双耦合谐振子共振仪实物图
信号源输出特定频率的方波信号,控制驱动电机产生对应频率的转动,驱动电机与驱动振子之间通过机械杆相连,这样驱动电机与驱动振子之间具有完全相同的振幅、相位。驱动振子、振子A1、振子A2之间通过弹簧连接,形成双耦合共振系统。为了测量振子的振动周期和振幅,在振子上安装BWT61CL型蓝牙加速度(陀螺仪)传感器,对振子运动的加速度进行实时测量。
2.2 振幅与相位差的测量方法
从加速度传感器得到的数据需要经过处理才能得到本文需要的振幅与相位差。从传感器得到a(t)数据以后,首先经过时间积分可以得到速度随时间的变化关系:
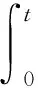
(14)
对速度进行时间积分以后即可得到位移随时间的变化关系:
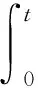
(15)
如图6(a)所示,当驱动频率为1.562 5 Hz时,双耦合系统陀螺仪输出的A1、A2振子加速度随时间的变化关系数据。经过时间积分以后可以分别得到图6(b)、(c)所示的速度时间关系和位移时间关系数据。可以看到双耦合振子在做简谐振动时,振子的平衡位置有轻微的抖动,这也是本模型可能出现测量误差的地方。
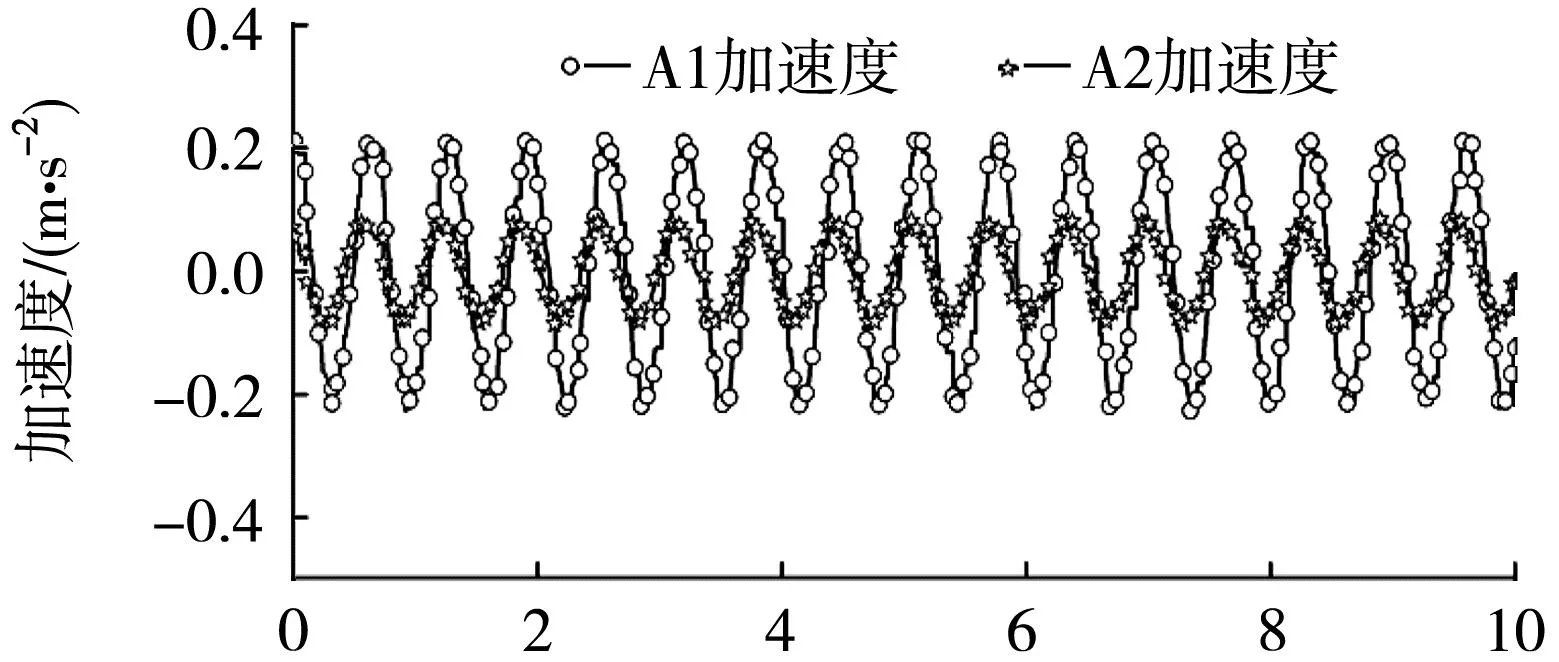
t/s(a)
得到振子的位移时间关系以后,对x(t)进行离散傅里叶变换得到:
(16)
A(f)代表的是每个不同频率下对应的振幅,即振子振动的频谱。从频谱中找到最大值及其对应的频率,即为此时振子受迫振荡的振幅和频率。如图7(a)所示,经过频谱变换以后可以得到各自振幅和频率的具体数值。两个受迫振荡的频率与驱动频率1.562 5 Hz吻合,一方面证实了稳定受迫的频率与驱动频率一致,另一方面验证了该方案测量频率和振幅可行。图7(b)画出了本文所有测量点受迫振荡频率测量值与驱动频率的相对误差,发现频率测量误差不会超过5.0%。

频率/Hz(a)
借鉴李萨茹图形测量相位差的原理[3],将两个振子的振动合成为如图8所示的李萨茹图形。因为振子做受迫振动的频率都等于驱动频率,所以李萨茹图形为椭圆。将测量数据拟合后即可得到椭圆方程:
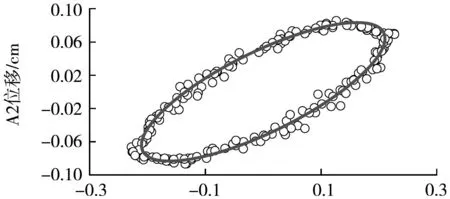
Al位移/cm图8 相位差的测量
中的相位差Δφ为0.692 rad。
3 双耦合谐振子模型的Fano共振特性
本文设计的双耦合谐振子共振仪,两个振子的质量分别为
m1=195.71 g ,
m2=299.80 g ,
两个弹簧的劲度系数为
k=6.445 N/m ,
小车运动过程中阻尼系数为
μ=0.216 ,
控制驱动电机的振动频率在[0.625 00 Hz,1.718 75 Hz]范围内,均匀选取36个测量点,得到了双耦合振子各自的幅频曲线和相频曲线。
图9所示为所搭建的双耦合共振仪测量得到的幅频曲线和相频曲线,其中点代表测量值、线代表的是理论值。从图中可以看出,双耦合谐振子振动过程中出现了两个共振主峰,并且振子A1在第一个共振峰附近的振幅接近零,即出现了Fano共振现象;在Fano共振的频率范围内两个振子之间的相位差发生了突变。另外,图9所示的幅频曲线既包含了经典的洛伦兹共振,也包含本文所展示的Fano共振。实验上幅频相频的变化规律、共振主峰的位置、Fano共振谷的位置都与理论结果吻合很好,说明该模型有很好的应用可行性。

频率/Hz(a)
4 结 论
本文先从理论上详细阐述了双耦合谐振子的共振特性,使用双耦合振子模型可以非常好地展现出反对称的Fano共振现象,同时在实验上设计了一种双耦合谐振子共振仪,给出了具体的实验测量方案,为Fano共振现象在基础物理和基础物理实验教学体系中的应用提供了理论和实践方案。本文为了测量振幅和相位差,结合离散傅里叶变换和李萨茹图形对双耦合谐振子模型,详细阐述了实验数据的处理过程,提高了该实验的综合性和挑战度,也得到了与理论值吻合非常好的Fano共振数据,为新实验的开设提供了充分的理论和实践依据。该实验还可以在劲度系数、阻尼系数、振子质量比等参数对Fano共振特性的影响等方面进行更深入的拓展研究。

