基于距离加权的矩形拟合方法研究

杨洋

（深圳市华汉伟业科技有限公司，广东 深圳 518000）

1 引言

机器视觉作为自动化系统中的“眼睛”和“大脑”，在推动智能制造向智能化、柔性化发展中起着重要作用。当前，机器视觉主要有测量、定位、识别、表面质量检测四大应用场景。光学测量作为实现非接触式测量的关键技术和手段，在自动化生产过程中起着重要作用。在平面测量中，点、线、圆和矩形等作为常用的设计要素和基本几何基元，解决上述基本几何基元的精确估计，是实现精确尺寸估计关键技术。

图像中的几何测量是图像分析和理解的重要内容，也是机器视觉的基础技术之一。为了满足装配、测量、品质分类等场景的要求，很多时候需要从图像中提取感兴趣的几何形状，如直线、圆、椭圆、矩形等，并对它们进行分析和计算，如求取它们的位置、方向、尺寸、面积、周长等参数。基于轮廓的矩形拟合方法主要存在以下两方面的问题：①图像轮廓的提取不一定准确，可能会受到噪声、遮挡、光照等因素的影响，导致轮廓不完整或不规则，从而影响矩形拟合的效果；②矩形拟合不一定稳定，可能会受到轮廓点分布不均匀或离群点的影响，导致矩形拟合结果与目标不一致或有较大误差。

为了解决上述问题，本文提出了一种基于距离加权的矩形拟合算法，通过引入一个加权函数来给不同距离的点分配不同的权重，从而降低噪声和异常值的影响，提高拟合精度和鲁棒性。加权函数，给距离近的点更高的权重，给距离远的点更低的权重，如Gauss、Huber、Tukey 等加权方法。

本文首先介绍了基于距离加权的矩形拟合方法的原理和步骤，然后通过实验验证了该方法在不同类型和条件下的图像上的有效性和优越性，并与其他常用的矩形拟合方法进行了比较和分析。最后，总结了本文的主要工作和创新点，并指出了未来需要改进和完善的方面。

2 研究与方法

矩形拟合是一种常用的图像处理技术，矩形拟合的基本思想是根据一组点集（xi，yi），根据预测值和真实值的误差的平方和最小的原则，完成矩形参数的估计，从而实现目标检测、识别或测量等功能。矩形是由相互正交和平行的四条直线构成的，因此很多直线拟合的方法，可以用来解决矩形拟合的问题。常用的直线拟合的方法有霍夫直线检测[1-2]、最小二乘直线拟合[3-5]、RANSAC直线拟合[6-8]等。本节首先介绍基于直线一般方程的最小二乘参数估计方法，然后结合聚类方法阐述点集划分的方法，最后给出矩形拟合的基本步骤和原理阐述。

2.1 最小二乘直线拟合

直线的一般表示形式为ax+by+c=0，其中a2+b2=1。设输入的点的坐标为（xi，yi）（i=1，2，…，n），根据最小二乘原理，可以建立目标函数为

2.2 坐标点集合聚类分割

输入的坐标是一个数组集合，由于矩形拟合需要获得每条直线对应的点的坐标，因此需要对数据点进行划分。本文坐标点分割的流程为：

1）根据轮廓点，获取凸多边形表示；

2）获取凸多边形中距离最远的两个点，确定为矩形对角线的两个点；

3）根据所述矩形对角线的两个点，确定矩形的另外两个点，确定方法为从剩余的轮廓点或凸多边形剩余的点中，寻找与所述矩形对角线的两个点分别形成的直线的夹角与90 度的差最小的像素点，以作为矩形中剩余的点。通过以下公式来寻找矩形中剩余的点：

4）将对寻找到的像素点进行位置校正，以使得校正后的像素点与所述矩形对角线的两个点分别形成的直线的夹角呈90°，可以通过以下公式来校正，以获得剩余的两个点：

5）计算各轮廓点与所述初始矩形四边条的距离，根据距离，将轮廓点分割到与四边条中最短距离的那一边，以将轮廓点分割为四组，每边对应一组。

2.3 基于距离加权的最小二乘拟合

本文提出了一种基于距离加权的矩形拟合算法，它通过引入一个加权函数，给距离近的点更高的权重，给距离远的点更低的权重，从而降低噪声点对拟合结果的影响。对于矩形的四条直线可以分别表示为

由于通过2.2 节已经把输入的边缘数据点分割为四条直线对应的数据点的集合，可以建立约束目标函数为

权重初始化为，对a、b、c、d、e、f和λ分别求偏导数，并令其偏导数等于0，可以获得参数a、b的初始解。后续可以根据Gauss-Newton 方法进行迭代计算，获得a、b最终解。a，b取值后，可以获得矩形的4 个点的坐标为

对于权重参数，常用的有三种：Gauss、Huber、Tukey，这三个权重函数的应用效果都很好。Huber 权重定义表示为

Tukey 权重定义表示为

式中，τ为削峰因子，δ表示点到对应直线的距离。这些点的权重在0～1 之间滑动变化，越接近理想拟合直线的点，所获得的权重越大，否则权重越小或者等于0。对于阈值τ的选择，通常经过距离的标准差近似估计获得。标准差的近似可以根据下式获得[10]：

3 结果与讨论

本文对6 个不同大小、不同旋转角度的矩形进行测试，获得Least Square、Huber 和Tukey 三种情况下的矩形拟合结果，获得拟合的矩形的中心（xc，yc）、主轴角度θ、主轴长L1和次轴长L2，Huber、Tukey 迭代次数为10 次。测试结果数据见表1。

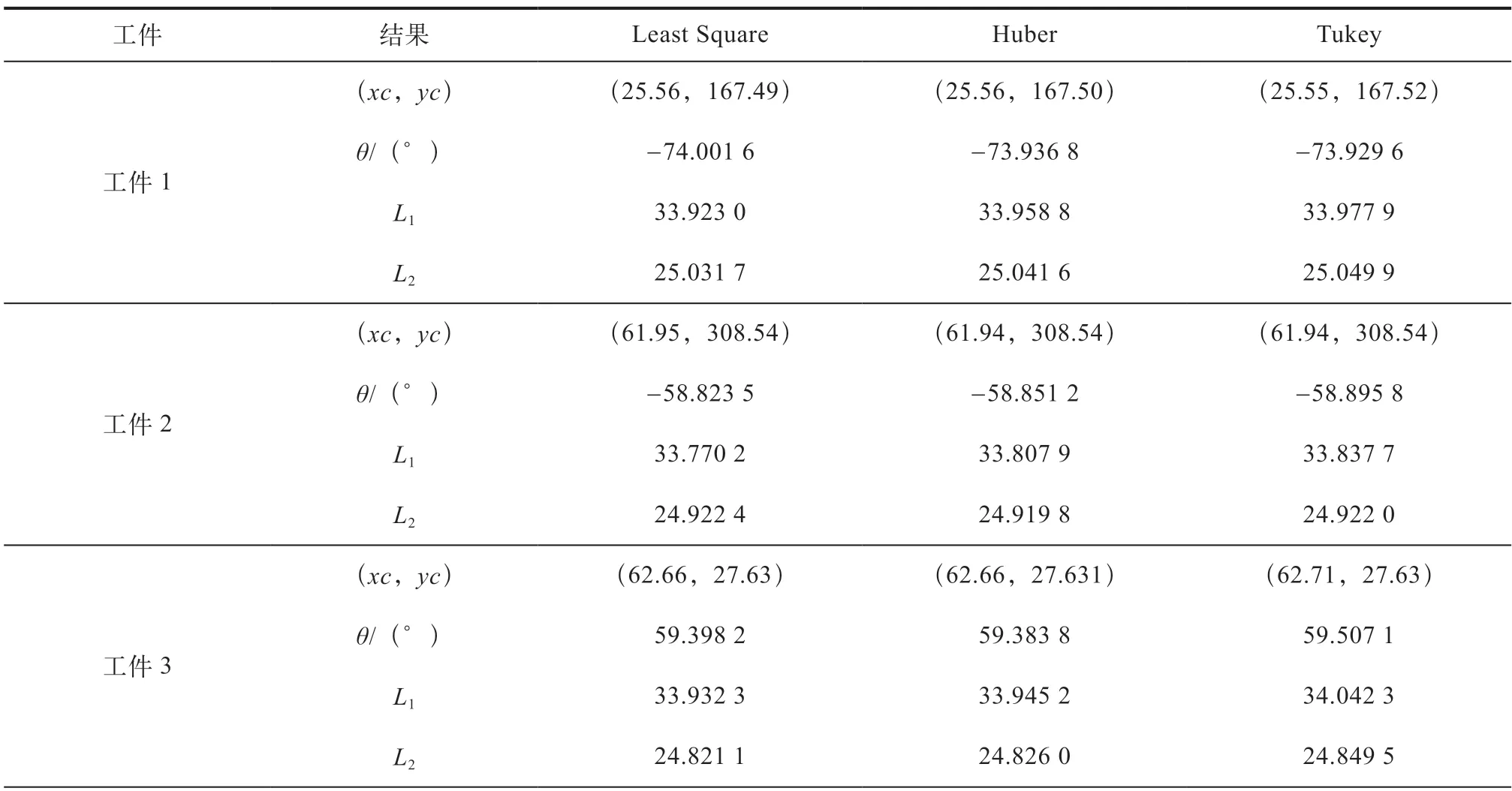
表1 测试结果数据

输入的图像数据自上而下，自左向右，依次为工件1～工件6，不同算法的检测结果如图1 所示。

图1 输入图像及不同算法检测结果

传统的方法通过提取点的坐标，通过直线拟合获得拟合的矩形信息。本文将2 个正方形进行拟合测试，测试结果表明本文方法的两个矩形的边长的差距更小，具有更好的拟合效果，测试结果如图2 所示，红色为传统方法的计算结果，绿色为本文计算结果，测试数据见表2。

图2 对比测试结果图

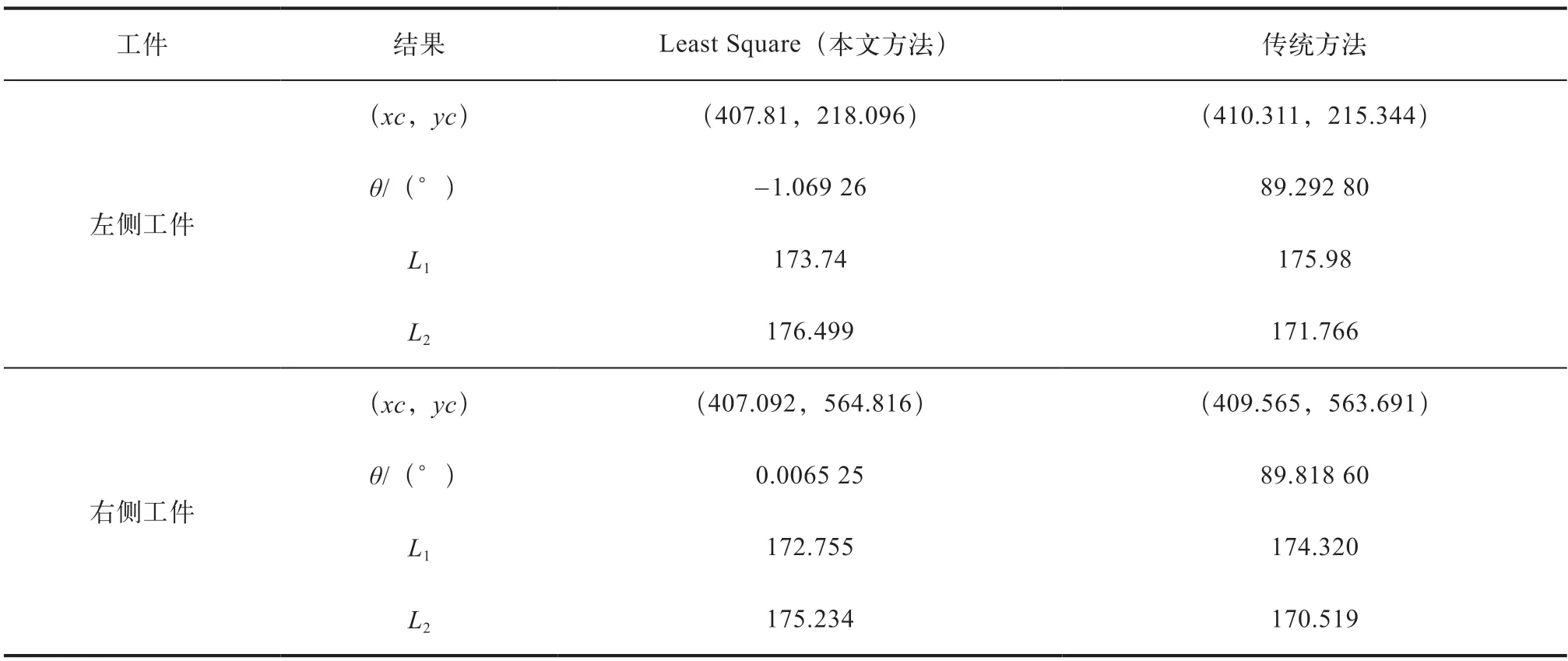
表2 对比测试结果数据

4 结束语

本文提出了一种基于距离加权的矩形拟合算法，通过引入一个加权函数，给距离近的点更高的权重，给距离远的点更低的权重，从而降低噪声点对拟合结果的影响。通过几何相似性，对输入的数据点进行分割，划分为四组直线数据，将矩形参数的回归转化为基于直线参数的回归，最后利用最小二乘法求解矩形模型的参数，利用了矩阵运算和迭代优化的方法，提高了算法的效率和收敛性。在机器视觉、智能制造等领域，可以利用矩形拟合来识别物体的位置、姿态、尺寸等信息，从而实现精准的控制和优化，具有很好的应用和落地前景。

矩形拟合在智能制造领域有广泛的应用场景，如在半导体、3C 电子制造、新能源等领域，成为解决测量工艺节点的关键技术。主要应用：半导体中掩膜板、Wafer晶圆的宽度、高度测量等；新能源领域中极片尺寸测量、极片清洗槽宽度测量等；3C 电子制造业中，手机面板、中框、背板等尺寸测量。