Sequential CI feedback fusion state filter for sensor networks
ZHENG Bai-Fu,GAO Yuan
(School of Electronic Engineering,Heilongjiang University,Harbin 150080,China)
Abstract:In order to reduce the computational burden of the sensor networked fusion center and fully utilize the sensor information,a sequential CI fusion Kalman filter with feedback structure is presented. This feedback structure sends back the state fusion prediction and the fusion error variance information of the fusion center to the local sensors as prior information,the filters work separately to calculate the new local state filter and its filtering error variance at the local sensor,which will be sent to the fusion center,and then the sequential CI fusion will be made according to the arriving orders of local estimators. A sequential fusion algorithm framework with feedback structure is established. Simulation experiments shows that this algorithm has good estimation performance and significantly reduces the computational burden of the fusion center. Compared with the centralized fusion filters,this algorithm reduces the computational pressure and burden of the fusion center,and improves the fault tolerance of the network. It has higher estimation accuracy than the sequential CI fusion filters without feedback.
Key words:feedback structure;sequential fusion;covariance intersection fusion
0 Introduction
The multi-sensor information fusion method is extensively employed in practical engineering fields such as target tracking,integrated navigation,industrial monitoring,and fault-tolerant control in recent years. Information fusion estimation is an important branch of multi-sensor information fusion theory[1]. The theoretical methods for multi-sensor information fusion filtering mainly consist of the centralized and distributed fusion filtering approaches. Although the centralized fusion filter keeps global optimality,it becomes computationally burdensome and exhibits poor fault tolerance when the number of nodes in the sensor network is large. The distributed fusion estimation approaches send each sensor's estimation to the fusion center for fusion,and can effectively reduce the computational burden on the center. The commonly used approaches for distributed fusion estimation include ones weighted by matrices,diagonal matrices,scalars,and CI fusion[2]. The first three approaches require calculating the cross-covariance matrices among local sensors which is challenging in practical applications. The CI fusion approach does not need the knowledge of the error cross-covariance matrices among those actual estimates,while it employs a convex combination of local estimation error variance matrices[3]. Compared with the distributed fusion approaches weighted by matrices,diagonal matrices and scalars,although its accuracy is decreased,the CI fusion approach avoids the calculation of the cross-covariance matrices which will result in increased computational burden. The common CI fusion approaches encompass the batch CI fusion algorithm,sequential CI fusion (SCI)algorithm and parallel CI fusion algorithm. The fast SCI fusion in [4]was presented to transform the huge pressure on the synchronous optimization and fusion into multiple sequential two-sensor fusion at the fusion center,significantly reducing the computational burden. In [5],a SCI fusion robust Kalman filter is presented,and the fusion filtering estimation obtained has higher accuracy than local filtering estimation. Its robustness is presented to ensure that the uncertainty of the actual filter error variance or its trace to the noise variance has the minmum upper bound. However,these algorithms primarily focus on enhancing information accuracy at the fusion center while neglecting improvements on local tracking performance and estimation accuracy.
In recent years,the state estimation problems in the networked systems are discussed extensively. The commonly used distributed fusion methods to obtain the local filters using their own sensor information,which is sent to the network center to fuse and form an open-loop mode,and the fusion center will fuse the filtering results with higher accuracy. To further enhance the overall accuracy of the networked system,the information feedback process from fusion center is added to the above open-loop structure to form a closed-loop mode,that is,the fusion estimation information obtained at the fusion center is used for forecasting,and then the fusion prediction value is fed back to each local sensor as prior information to promote a better and more accurate closed-loop estimation. In[6],the fusion filter with feedback structure is presented for dynamic systems first,and it was proved that its tracking performance and overall accuracy achieved through distributed fusion with feedback structures are identical with those attained via centralized fusion,that is,the distributed fusion estimation with feedback structure has global optimality. Its essence is to employ the feedback structure to reduce the tracking error of each local sensor and improve the local tracking performance. In[7],the feedback distributed recursive fusion estimation of multi-sensor systems with correlated noises is studied,and it is proved that the distributed fusion with feedback structure has the same accuracy as the centralized fusion. An optimal distributed fusion filter with feedback structure is presented for multi-sensor linear discrete-time stochastic systems in[8],which has the same accuracy as the centralized fusion filter when compared. In[9],a distributed fusion optimal predictor with feedback structure is presented for a multi-sensor systems with random parameter matrices and correlated noises,and has the same estimation accuracy as the centralized fusion predictor. A distributed Kalman filter with feedback structure for multi-sensor systems is presented whose filter error matrix has singular covariance in[10],its tracking performance is equivalent to that of a centralized fusion filter. Although those above distributed fusion estimation algorithms with feedback structure form the optimal recursive fusion,the computational burden of calculating the cross-covariance matrices among the local estimators is huge,and moreover,the fusion center experiences significant leisure time while waiting for all sensor data to arrive before performing fusion.
Toovercome the limitations of the common distributed fusion methods with large computational burden and large leisure time at the fusion center,a SCI fusion filter with feedback structure for multi-sensor networked systems is presented. By utilizing the SCI fusion algorithm,this algorithm not only avoids the calculation of the cross-covariance matrices among sensors,but also enhances overall fusion accuracy. Furthermore,this algorithm structs an efficient scheduling of processing time at the fusion center,named as the SCI feedback fusion algorithm.
1 Problem formulation
Considerthe linear discrete time-invariant multi-sensor networked system
x(k+1)=Φx(k)+Γw(k)
(1)
yi(k)=Hix(k)+vi(k),i=1,2,…,L
(2)
wherekis the discrete time,x(k)∈Rnis the state,yi(k)∈Rmi,i=1,2,…,Lis the measured output of sensori,w(k)∈Rris the process noise,vi(k)∈Rmiis the measurement noise,Φ,ΓandHiare the constant matrices with suitable dimensions,andLis the number of sensors.
Assumption 1w(k) andvi(k) are uncorrelated white noises with zero means and variancesQ(k) andRi,j(k),respectively
E[w(k)]=0,E[vi(k)]=0
(3)
(4)
where T is the transpose,andδijis the Kronecker function,i.e.δii=1,δij=0(i≠j).
Assumption 2 The initial statex(0) is mutually independent ofw(k) andvi(k)
(5)
withE[x(0)]=μ0
E[(x(0)-μ0)(x(0)-μ0)T]=P0
(6)
To enhance the utilization rate of fusion estimation information,a feedback structure is added based on the previous fusion estimation,that is,the filtering information of the local sensor is sent to the fusion center,and the fusion center performs fusion filtering and calculates the one-step fusion prediction estimation and the corresponding error variance matrices,which are fed back to the local sensor as the prior information to participate in the local next-step filtering estimation calculation. After that,the new local filter value is sent to the fusion center for the next fusion. The whole process forms a complete feedback mode. To further reduce the leisure time and computational burden at the fusion center,the "serial" method is used to estimate the fusion state. Fig.1 shows the SCI fusion filter structure with feedback structure,which is constructed by using the SCI fusion algorithm,named as SCI feedback fusion filter.
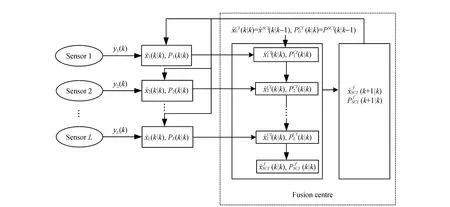
Fig.1 SCI feedback fusion filtering structure
2 SCI feedback fusion filtering algorithm
2.1 Filter estimation at sensor nodes
In the networked system,the sensor node is regarded as the local sensor,and the fused predictor is used as the prior information to obtain the filter.
Lemma 1[11]According to Projection Theory,for the networked system (1)and (2),the local optimal Kalman filters are obtained under Assumption 1 and 2
(7)
(8)
(9)
(10)
Pi(k|k)=[In-Ki(k)Hi]Pi(k|k-1)
(11)
Pi(k+1|k)=ΦPi(k|k)ΦT+ΓQ(k)ΓT
(12)
(13)
2.2 SCI Fusion estimation at fusion center
Lemma2[12]The SCI fusion algorithm is obtained by performingL-1 steps of SCI fusion estimation by the arrival order
(14)
i=2,…,L
(15)
(16)
(17)
(18)
Remark1 Since the sequential fusion approach is adapted,the fusion center only used 2 groups of filter estimation each time,and the minimizing performance index by the optimal weighting coefficientw(i-1)is a simple one-dimensional nonlinear optimization problem,which can be solved quickly by the golden section method.
2.3 SCI feedback fusion filtering algorithm
Theorem 1. Under Assumption 1 and 2,the SCI feedback fusion Kalman filter for the networked system (1)and (2)is formed as
at fusion center:
(19)
(20)
(21)
(22)
(23)
(24)
at sensor nodes:
(25)
(26)
(27)
(28)
(29)
Prove. Substituting (8)and (10)into (7)yields
(30)
Ψfi(k)=[In-Ki(k)Hi]Φ
(31)
and the filter error variance matrices satisfies the Lyapounov equation
Δfi(k)
(32)
where
Δfi(k)=[In-Ki(k)Hi]ΓQ(k)ΓT[In-
(33)
Based onLemma 2,the fusion center use the SCI fusion algorithm. TheL-1 steps two-sensor SCI fusion filters and error variance matrices are obtained as
(34)
(1-w(i-1))×(Pi(k|k))-1]-1,i=2,…,L
(35)
where
(36)
(37)
The sequential fusion resultsare used to make a one-step prediction at the fusion center
(38)
(39)
(40)
(41)
Substituted (38)~(41)into equation (7)obtains the local filter (25)at the next step. Then substituting (39)and (40)into equation (11)yields (28). Eq. (19)~(24)is obtained by substituting (25)and (28)into (34)~(37). The prove is completed.

3 Simulation example
Consider a three-sensor tracking system
(42)
yi(k)=Hix(k)+vi(k),i=1,2,3
(43)



Fig.2 Fusion filter tracking curves
The accumulated error curves are shown in Fig.3,where the solid curves represent the accumulated error squares of the SCI feedback fusion filtering estimation,the dashed curves represent the accumulated error squares of the SCI fusion filtering estimation,and the dotted curves represent the accumulated error squares of the centralized fusion filtering estimation respectively. The accuracy of the SCI feedback fusion Kalman filter is verified to be higher than that of the SCI fusion Kalman filter,but lower than that of the centralized fusion Kalman filter.
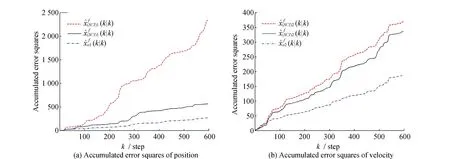
Fig.3 Accumulated error squared curves
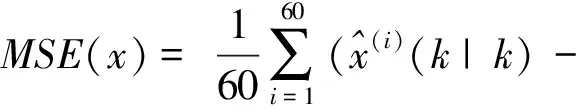
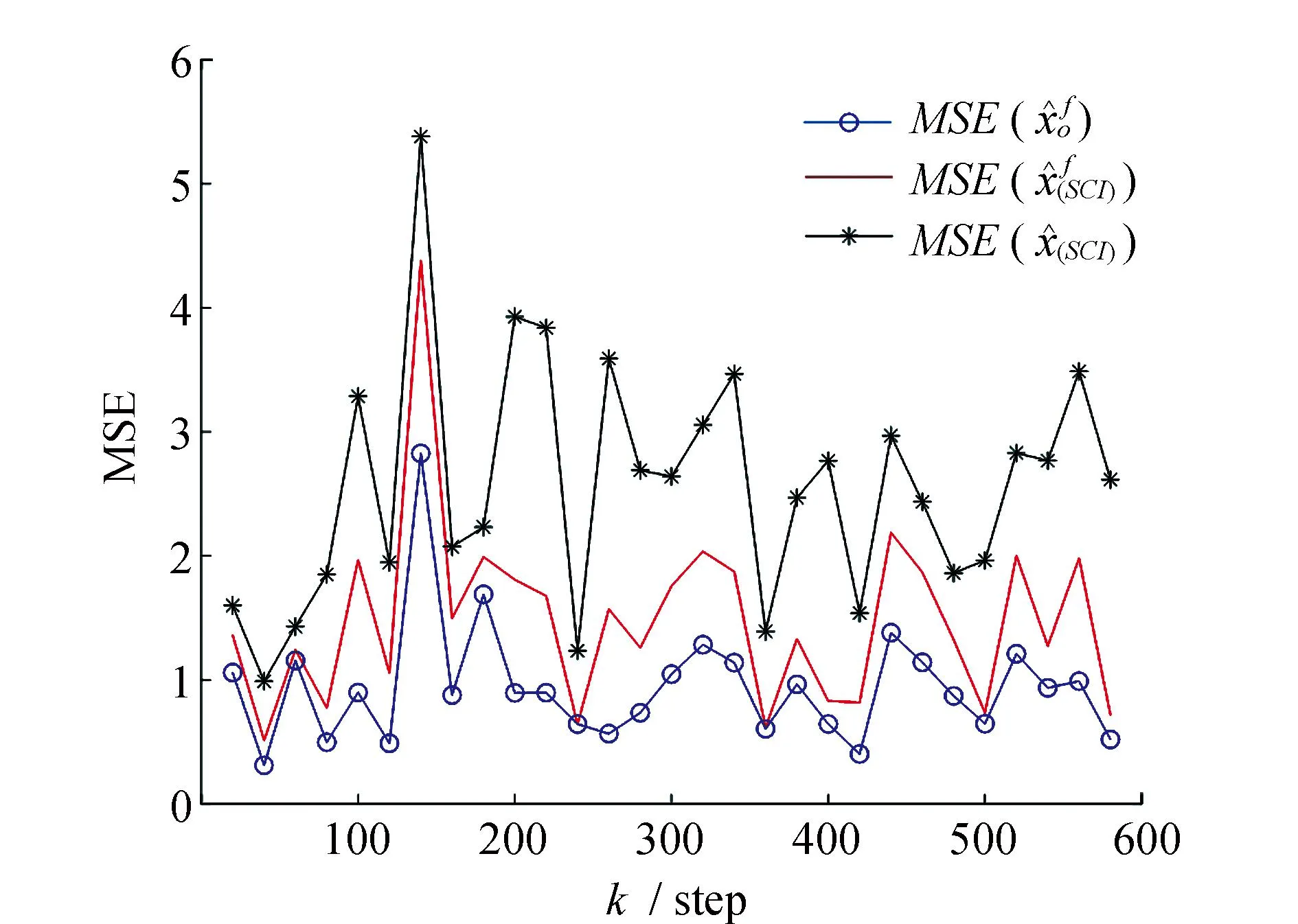
Fig.4 MSE curves of different fusion algorithms at fusion center networked
4 Conclusions
For the multi-sensor networked systems,the SCI feedback fusion algorithm has been presented which introduces a feedback structure,and it has been proved that its accuracy is higher than the previous SCI fusion and local sensors. The simulation example verifies the effectiveness and accuracy of the SCI feedback fusion estimation algorithm,which reduces the computational burden and the leisure time of the fusion center.

