土体类型差异对大跨度综合管廊抗震性能影响

戎密仁, 冯超, 庞银萍, 陈耀辉, 刘喜坤, 戎虎仁, 马骁

1. 河北地质大学 a. 城市地质与工程学院, b. 河北省地下人工环境智慧开发与管控技术创新中心, 河北 石家庄 050031; 2. 首尔科学综合大学院大学, 韩国 首尔 06983; 3. 河北雄安京翼质量检测服务有限公司, 河北 雄安 071700; 4. 山西大学 电力与建筑学院, 山西 太原 030006; 5. 大连交通大学 国际教育学院, 辽宁 大连 116028

0 引言

地下综合管廊的抗震性能对其正常使用影响较大, 国内学者针对这一问题进行广泛, 并取得了显著成果, 如: 史晓军等[1]、 仉文岗等[2]、 魏奇科等[3]和陈守一等[4]基于相似理论, 利用振动台试验系统,研究峰值加速度地震波作用下管廊各部位及周围土体的动力响应, 得到不同PGA 作用下管廊各部件及周围土体位移、 应力分布规律; 岳庆霞[5]基于位移时程输入法, 分析了地震波输入方向、 人工边界类型及土体—结构作用面属性差异对管廊动力响应准确性影响; 研究者基于动力时程分析法, 分析了管廊破坏特征及非一致地震激励下管廊动力响应差异, 得到了土体—结构相互作用面的分离、 滑移情况及管廊受力薄弱部位[6-8]; 部分学者研究了不同分析方法在管廊抗震分析中的适用性及精确度问题, 为管廊抗震相关工作的研究提供新思路[9,10]; 也有部分学者基于有限元理论, 研究不同地震波输入方式作用下综合管廊动力响应, 得到了综合管廊动力响应差异规律[11,12]; 王长祥[13]利用ABAQUS 软件, 分析不同入射角度地震波作用下预制综合管廊的整体抗震性能, 得到不同入射角度下管廊内力、 位移分布规律; 王程[14]基于整体动力时程分析法, 研究管廊接缝张开量与地震波峰值加速度关系, 得到二维模型计算时张开量的折减系数; 杨剑等[15]利用FLAC 软件, 研究液化土体埋覆下综合管廊抗震性动力响应, 得到土体液化后的加速度、 位移、 孔压比等参数变化规律。

综上所述, 研究者主要针对地震波类型差异、 不同方法差异对管廊的抗震性能影响进行研究, 而关于土体差异影响下管廊抗震性能变化方面的研究相对较少, 对大跨度综合管廊的抗震性能分析少之又少; 然而, 土体性质差异对于地下结构的安全性、 耐久性影响较大, 且土体类型数量较多、 物理参数复杂, 不同土体对地震响应程度不同, 易造成地下结构各部位受力不均, 导致地下结构破坏; 在地下综合管廊工程中, 为了避免不同土体类型地震响应差异造成的结构坍塌、 内部管道破裂等灾害, 对不同土体埋覆下综合管廊的抗震性能研究就显得极其重要、 迫切。 本文以济南市水厂南路综合管廊工程项目为依托, 通过动力时程分析法与有限元理论模拟研究相结合的方法, 系统研究不同土体对大跨度综合管廊的抗震性能影响;该研究结果为国内外大跨综合管廊在抗震设计、 规划与现场实施等方面提供指导。

1 工程背景与相关参数

1.1 大跨综合管廊结构

济南市水厂南路综合管廊全长1 617.864 m, 为综合舱和电力舱组成的矩形双舱结构(图1); 其中: 综合舱净宽4 000 mm、 净高3 500 mm; 电力舱净宽2 300 mm、净高3 500 mm; 结构地板、 顶板、 侧壁厚度为500 mm、 中隔板厚300 mm, 均采用C35 混凝土浇筑,其混凝土参数如表1 所示; 上方覆土厚度为3 500 mm。

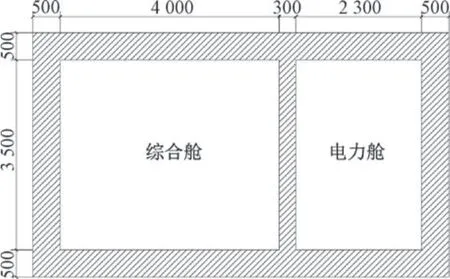
图1 济南水厂南路综合管廊示意图(mm)Fig.1 Schematic diagram of pipeline corridor of Shuichang South Road in Jinan City

表1 混凝土物理参数Table 1 Physical parameters of concrete

1.2 土体类型及力学参数

建设场地属于第四系地貌单元, 为黄河冲积平原, 场地地势较低, 地形较平坦; 主要由人工填土及洪积成因的粉土、 粉质黏土及砂土组成(表2)。

表2 济南市水厂南路岩土工程地质评价Table 2 Geotechnical engineeringgeologl evaluation of Shuichang South Road in Jinan City

因人工填土的力学性能存在较大不确定、 且分布深度较浅, 对地下综合管廊的受力影响较小; 本文仅对粉土、 粉质黏土、 砂土埋覆下综合管廊的抗震性能进行分析研究, 该区域的典型土体参数见表3[17]。

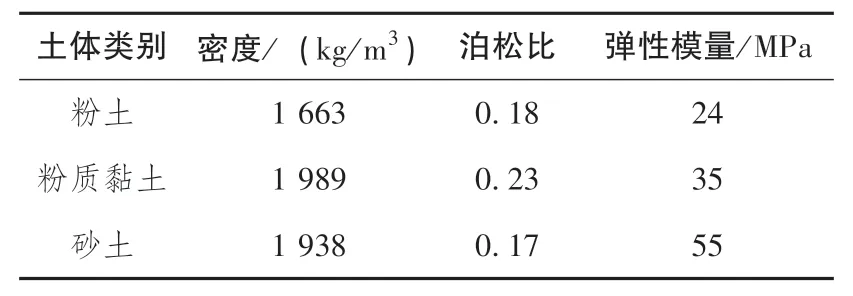
表3 土体物理参数Table 3 Physical parameters of soil

1.3 地震参数确定

该地处于齐河—广饶断裂带、 桑梓店断裂带、 卧牛山断裂带影响范围之内, 抗震设防烈度为VI 度,场地类别为III 类, 抗震设防烈度峰值加速度为0.1 g, 罕遇地震加速度为0.22 g[18], 地震动加速度反应谱特征周期为0.65 s, 且无砂土液化现象。

2 大跨度综合管廊抗震理论

2.1 土体—结构相互作用确定分析

土体—结构的相互作用对综合管廊的动力响应有重要影响, 由于土体与混凝土材料物理性质差异性较大, 导致土体与管廊结构之间接触力学性质较为复杂。 为确保理论模拟结果准确性, 拟采用接触面力学分析法研究土体与管廊结构二者之间的相互作用。

接触面的力学关系通过定义主、 从面关系及接触面属性来实现, 即: 当土体与结构在相互作用面法线方向发生接触时, 二者之间存在传力关系, 反之则不存在; 同理, 当在相互作用面切线方向发生接触时,可进行切向力的传递, 且切应力τ大于极限切应力τcrit时, 二者处于滑动状态, 反之则处于粘结状态;极限切应力可表示为:

式中:p为法向力,μ为摩擦系数。

2.2 黏弹性边界确定分析

为消除地震波的反射及低频失稳等影响, 在在动力分析模型的四周施加黏弹性边界, 即在模型四周和底部设置黏弹性边界—弹簧阻尼元件, 弹簧刚度及阻尼系数确定过程如下。

地震纵波波速:

地震横波波速:

式中:λ为拉梅常数;ν为泊松比, E 为弹性模量;ρ为土体密度。

弹簧法向刚度:

弹簧切向刚度:

法向阻尼系数:

切向阻尼系数:

式中:α为平面波与散射波幅值比, 通常取0.8;G为等效剪切模量;β为物理波速与视波速的比值,通常取1.1;A为边界节点所代表的面积和, 取0.9;γ为结构几何中心到人工边界点的距离[19,20]。

2.3 等效节点荷载分析

在反射波被完全吸收后, 可将振动问题转化成四周及底部节点的自由场运动问题, 即地震波加速度荷载以等效节点力的形式施加在四周边界节点上。 此时的等效节点力主要包括自由场位移计算、 地震波传播速度计算及等效节点力计算3 部分, 节点应力状态与地震波速度及位移的函数关系可表示为:

式中:K为弹簧元件的刚度系数,C为弹簧元件阻尼系数,u为人工边界节点处的位移向量,u·为人工边界节点处的速度向量。 边界节点的等效荷载为:

式中: A 为节点影响面积。

经反射后的地震波到达地表时, 其三维场应变可表示为:

当S 波入射时, 边界节点任一时刻的位移及速度可表示为:

底面等效节点荷载可表示为(以底板下部为例,其他几个面同理):

通过上式可将任一时刻地震波加速度转化成模型四周各节点的节点力, 加速度时程曲线则转化成各节点力随时间变化的幅值曲线, 进而完成地震波加速度等效节点荷载的转化, 可实现模型地震等效荷载的施加。

3 理论模型建立

3.1 地震波选取

选取埃尔森特罗N-S 方向地震波能量较为集中的前15 s 作为地震荷载, 进行分析计算并将峰值加速度调整为0.1 g, 以实现理论模拟济南地区抗震设防烈度, 校正后的地震波加速度时程曲线如图2 所示。

图2 N-S 方向0.1g 地震波时程曲线Fig.2 Time history curve of 0.1g seismic wave in N-S direction

3.2 本构模型选择

为研究不同性质土体差异对综合管廊抗震性能的影响, 在建立理论模型时, 应将土体和混凝土结构的本构模型分别考虑, 具体为: ①考虑选用黏弹性边界进行了基本假设, 在动力分析时的土体采用弹性本构模型; ②分析管廊在地震荷载作用下的受力状态, 混凝土本构模型采用塑性损伤模型(CDP 模型)。

3.3 土—结相互作用设置

为准确研究地震荷载作用下管廊结构与周围土体的滑移现象, 拟采用“表面与表面接触” 方法实现管廊外表面与埋覆土体之间的接触, 建立二者之间的相互作用关系。

将地下综合管廊外表面设置为主表面, 与其接触土体表面设置为从表面, 跟踪方式选择有限滑移方式; 将接触面法向的接触属性定义为“硬” 接触, 切向接触属性定义为“罚” 接触, 摩擦系数取为1, 所得的土体—结构接触对如图3 所示[16]。

图3 土体—结构相互作用接触对Fig.3 Soil-structure interaction contact pair

3.4 地震波输入及黏弹性边界实现

在黏弹性边界完全吸收反射波时, 地震波的输入问题可转化成边界节点的自由场运动问题, 即将地震波加速度采用等效节点力的方式作用在模型边界节点上; 具体黏弹性边界及等效节点力的实现方式如下:

第一步: 对所要施加黏弹性边界及等效节点荷载的模型外部边界面施加大小为1 的均布荷载, 并约束其法线方向位移, 计算得到边界节点影响面积及反力文件;

第二步: 提取边界节点编号及坐标, 并将地震波加速度积分得到相应的地震动速度及位移荷载文件;

第三步: 将地震波时间间隔、 模型尺寸、 土体弹性模量、 泊松、 密度等参数输入到基于黏弹性边界及地震动输入理论编制的MATLAB 程序中, 计算得到荷载、 节点幅值及弹簧阻尼器单元文件, 最后导入inp文件实现黏弹性边界及等效节点荷载的施加; 等效节点力、 黏弹性边界实现分别如图4、 图5 所示。

图4 地震加速度等效节点力Fig.4 Equivalent nodal forces of seismic

图5 黏弹性边界Fig.5 Viscoelastic boundary

3.5 大跨综合管廊抗震性能研究工况

因剪切波(S 波) 对地下管廊结构的抗震性能影响较大, 故在X 方向输入地震波模拟S 波作用; 通过施加砂土、 粉土、 粉质黏土等3 种埋覆土体, 来分析研究埋覆土体性质差异对综合管廊抗震性能影响, 进一步分析其相应的位移、 加速度、 应力响应等参数。

4 抗震特性与机理分析

4.1 位移变化及机理研究

在管廊结构顶部、 底部选取特征点, 得到相同地震荷载条件下, 砂土、 粉土、 粉质黏土等3 种土体埋覆下结构的位移变化特征和不同方向的位移时程曲线(图6)。 分析可知: ①因地下管廊自身刚度较大, 在地震荷载下管廊自身变形较小; ②在S 波地震荷载作用下, 3 类土体埋覆下综合管廊的位移时程曲线趋势基本一致, 但不同方向的位移有所差异; 均在地震波输入方向(X 向) 位移远远大于Y、 Z 方向的位移,且管顶位移均大于管底位移; ③粉土埋覆下综合管廊的位移最大为0.145 m; 砂土埋覆下综合管廊的位移最小为0.102 5 m。

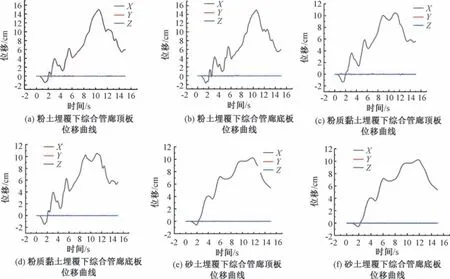
图6 不同土体埋覆下综合管廊位移时程曲线Fig.6 Time history curve of displacement of comprehensive pipe gallery under different soil coverings

根据理论分析结果得到3 种不同土体埋覆下综合管廊顶板、 底板的位移汇总表4。 分析可知: 砂土埋覆下综合管廊的相对位移差与峰值位移规律相同, 其相对位移最小为2.774×10-4m, 粉土埋覆下综合管廊的相对位移差最大为6.02×10-4m。

表4 综合管廊顶板、 底板位移差Table 4 Displacement difference between roof and floor of pipe gallery

综上分析可得出: ①3 种土体埋覆下地下综合管廊顶板、 底板的峰值位移及位移差均随土体弹性模量的增大而减小; ②在相同地震峰值加速度作用下, 随埋覆土体弹性模量的增大, 土体的刚度也随之增大,位移响应随之减小, 顶板与底板的位移差也逐渐减小; ③下部土体发生较大的位移变形, 比上部土体先发生破坏。

4.2 加速度响应分析与机理研究

分析3 种不同土体埋覆下综合管廊顶部与底部沿X 向的加速度时程曲线(图7) 和加速度放大系数(表5) 可知:

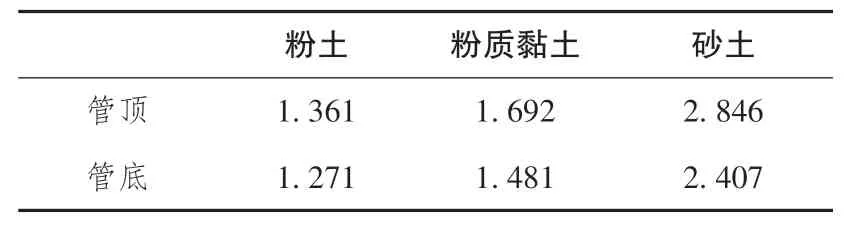
表5 管廊顶板、 底板加速度放大系数Table 5 Acceleration amplification coefficient of roof and floor of pipe gallery

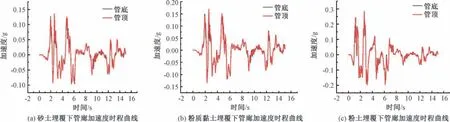
图7 不同土体埋覆下综合管廊加速度时程曲线Fig. 7 Time-history curve of acceleration of pipe gallery under different soil coverings

①随土体弹性模量的增大, 结构—土体相互作用振动频率接近地震振动频率, 造成加速度增大; ②管廊下部土体率先发生破坏, 地震波能量在传播过程中耗能较大, 则管廊下部加速度小于顶部加速度; ③加速度和放大系数变化规律与位移响应规律不同, 但整体上均随土体弹性模量的增大而增大, 且管顶峰值加速度大于管底; ④砂土埋覆下综合管廊峰值加速度放大系数最大为2.846, 粉土埋覆下综合管廊加速度放大系数最小为1.271。

4.3 应力响应分析与机理研究

图8、 图9 分别表示3 种不同土体埋覆下综合管廊顶板、 底板、 中隔板处X 方向的应力时程曲线、 整体结构应力分布规律云图, 分析可知: ①3 种不同土体埋覆下综合管廊的应力与加速度变化规律均相同,与埋覆土体的弹性模量呈正比, 中隔板应力最大, 管顶应力次之, 管底应力最小; ②最大峰值应力为0.12 MPa, 在砂土埋覆下中隔板位置处, 远远小于混凝土极限抗拉强度; ③3 种不同土体埋覆下管廊结构的整体应力分布规律一致。

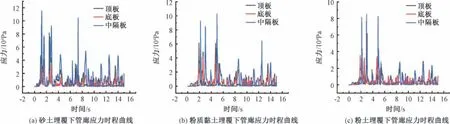
图8 不同土体埋覆下综合管廊应力时程曲线Fig.8 Time history curve of stress of pipe gallery under different soil coverings

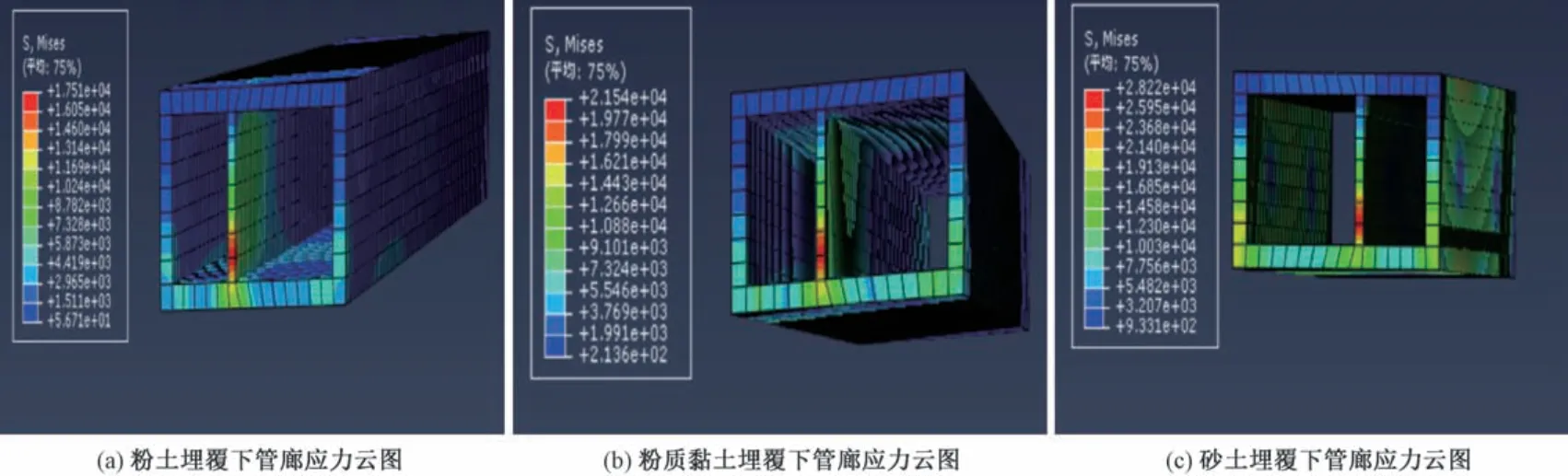
图9 不同土体埋覆下综合管廊应力云图Fig.9 Stress cloud diagram of pipe gallery under different soil coverings

5 结束语

基于黏弹性边界理论和ABAQUS 有限元思想, 系统研究了砂土、 粉土、 粉质黏土3 种不同类型土体埋覆下双舱大跨综合管廊结构的抗震性能, 阐述了其力学特性与机理, 得到如下结论:

1) 研究并确定了大跨综合管廊结构中, 3 种覆土影响下管廊结构抗震参数; 在分析研究土体-结构之间的相互作用机理、 黏弹性边界、 地震波荷载施加等方面理论基础之上, 提出了大跨综合管廊的抗震理论, 明确了类似结构的抗震分析研究理论。

2) 在3 种土体覆土下管廊结构抗震理论, 研究并提出了理论模型中的地震波施加方式、 土体与管廊结构的本构模型与相互作用关系、 黏弹性边界等关键性问题的实施方法。

3) 3 种不同土体埋覆下综合管廊的位移以X 方向为主, 但随土体弹性模量的增大而减小; 粉土埋覆下管廊结构的位移最大为0.145 m, 位移差的最大值为0.602 mm; 砂土埋覆下综合管廊结构的加速度最大,且管顶加速度均大于管底加速度, 峰值最大为0.284 6 g; 最大应力均在地震荷载输入5 s 时, 管廊结构中隔板处应力大于底板、 顶板; 其峰值应力为砂土埋覆下综合管廊的中隔板板位置, 为0.12 MPa。