计算音系学:原理、方法及未来发展

赵永刚 黄捷

(西安外国语大学 英文学院, 陕西 西安 710128)

0 引言

随着世界科技的飞速发展,交叉学科不断繁荣,计算语言学研究也取得了长足的进展,其中计算音系学的兴起正是这一领域的重大成果之一。 计算音系学既属于音系学,又属于计算语言学,是音系学的跨学科研究。 关于计算音系学理论的思考,最早可追溯到早期SPE(Sound Patterns of English,简称:SPE)音系学的规则推导理论,即有序排列规则可组构成有限状态技术(Finite State Transducer,简称:FST)的理念。 尽管计算音系学研究涉及形式语言学理论,以及各种不同的研究方法,但这些研究的共同目标都表现为使用计算方法来分析和探究自然语言的复杂语音和音系现象,也就是在一系列“逻辑上的可能形式”中找出音变规律。 如今,这一研究领域已广泛涉及语音识别与合成(技术)、语音处理和语音交互等诸多方面。 自20 世纪90 年代初以来,音系学研究从基于规则的理论开始转向基于制约条件的理论框架,如OT 理论(Optimality Theory,简称:OT)(Prince et al.,2004),激发了语言学家对如何使用有限状态技术将OT 理论加以模式化的深入探讨,此后对OT理论、自动学习、语法与语音/音系界面等方面的研究皆成为这一领域的热点论题。 随着自然语言信息处理和人工智能的步步深入,计算音系学在未来的若干年内必将成为语言学的一个新的重点研究领域。

计算语言学是计算机科学、数学、逻辑学、语言学等学科结合下产生的一门新兴交叉学科,旨在通过分析自然语言现象,建立数学模型,将语言形式化,进而利用计算机软件处理、模拟并生成人工语言。 形式语言学建立了一整套形式化的原则和规则系统,试图从语言结构内部寻找对语言现象的解释。 计算音系学是计算语言学下的一个分支,主要任务是用计算方法或者形式化的方法来阐释自然语言中复杂的语音现象,探索音变规律。 计算音系学和语音技术、语音识别、语音模拟等息息相关。 本文通过厘清计算音系学的定义、研究方向和研究范围,阐述计算音系学的有限状态模式和联结主义这两大主要研究方法,并以具体语言现象为例,分析两种研究方法的具体应用,旨在唤起国内语言学界对计算音系学的重视,阐释该学科研究现状和推进学科前沿,激发语言学家、计算机科学家以及自然语言处理方面的专家进一步认识语言学的计算方法和认知理据,促进人工智能向更纵深层次发展。

1 计算音系学的基本定义和发展历程

1.1 计算音系学:计算语言学的分支

计算语言学是集计算机科学、数学、逻辑学、语言学于一体的交叉学科,旨在通过计算机来进行人类语言研究,和计量语言学、数理语言学、自然语言理解、自然语言处理、人类语言技术等学科密切相关,基本架构就是通过研究分析自然语言,构建数学模型,利用计算手段对形式化的语言进行编辑处理,最终目标是模拟生成人工语言。 计算语言学的构成要素可以用下图表示(Halvorsen,1988:20;袁毓林,2001:159):

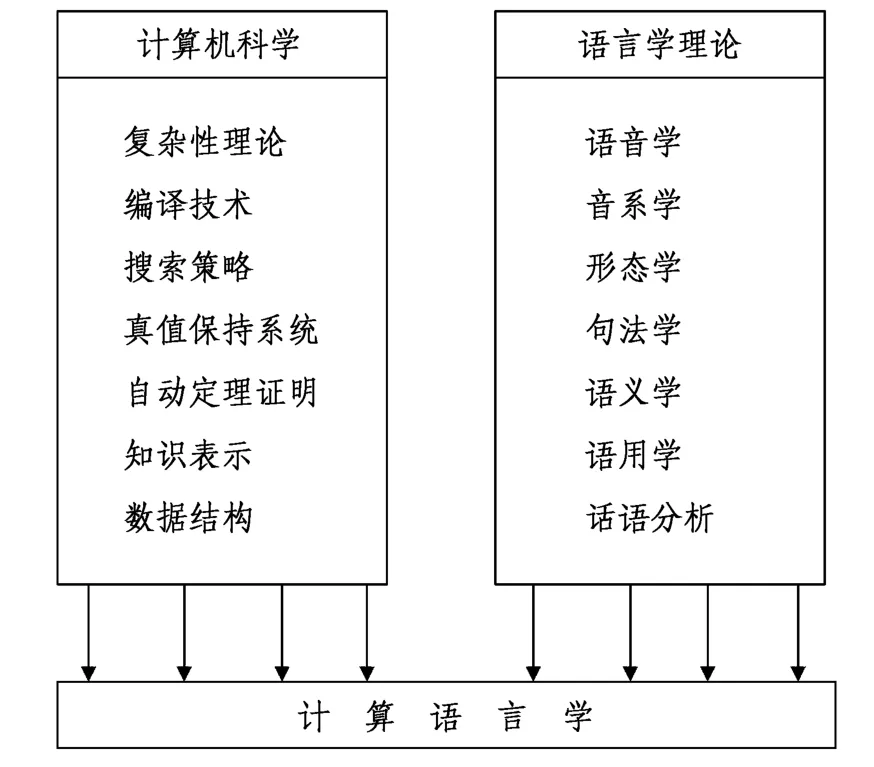
图1 计算语言学架构图

目前,计算语言学研究的重点主要放在自动编排、自动分析和自动化研究上。 语言学家以计算机为工具,来进行诸如文本信息检索、文献自动分类、自动文摘、语音自动识别与合成、机器翻译以及文本信息的提取和过滤等复杂工作,进行纵深层次的语言分析和语言处理。 计算语言学有五个任务:(1)语言学问题,即从语言学角度出发去看待计算语言处理的问题。 自然语言处理需要解决诸如语句分割问题、句子的语义等语言学问题。 (2)语言的形式化,我们需要用数学工具把语言学问题表述成语言模型,并将研究的问题在语言学上加以形式化,严密而规整地表示出来,才有利于语言处理。 (3)计算形式化,语言模型需要被计算机的算法描述成为一个可计算的模型,从而实现计算形式化,计算机语言中的前向或后向最大匹配算法、动态规划算法等,就是为了实现计算的形式化。 (4)编程阶段,完成了前三个任务之后,才可以开始这个任务,即使用编程语言实现这个计算模型。 (5)评估,我们需要对计算机处理的结果进行评估,通过计算某些指标,如准确率、召回率等,评估任务完成的情况。 语言学理论进入计算机程序的过程,Halvorsen(1988:201)用图2 表示:

图2 语言学理论到计算机程序流程图

计算语言学和自然语言处理都是对自然语言的研究,但研究的侧重点存在差异。 前者强调建立纯数学的语言模型,用纯粹数学的方法来描述语言结构,后者是要让计算机像人一样能懂语言,其本质是要把语言学数学化。 两者研究的核心问题都是语言的自动理解和自动生成。 自然语言处理从计算机科学的角度出发,主要用来进行语言计算(语音与音系、词法、句法、语义、语用等各个层面上的计算)、语言资源建设(计算词汇学、术语学、电子词典、语料库、知识本体等)、机器翻译与机器辅助翻译、手写和印刷体文字识别、语音识别及文语转换、信息检索(搜索引擎、信息抽取与过滤)、文本分类等。 自然语言处理的研究是为了促进机器的智能化,从而实现信息的有效处理(王萌等,2015:151),而计算语言学的主要应用在机器翻译、语音识别、语音合成、语料库分析等领域,更专注于理解语言规律,提高语言输入和输出水平。

计算音系学是计算语言学的最新领域之一,计算音系学把计算语言学理论、技术和方法应用于语音研究,把语言学家、音系学家和计算机科学家等不同研究群体聚集在基于制约的音系领域,借鉴基于制约的语法以及约束编程的见解,探索在现代非线性音系学中利用制约条件,来形式化和实现基于制约的音系学。 计算音系学是利用数理计算和形式化方法来分析自然语言中复杂的语音现象,总结出音变规律的语言科学。 史蒂文·伯德(Steven Bird)(2003:30)认为计算音系学是语言形式化和计算技术在音系信息表征和语音处理中的具体应用。 计算音系学的出现,为语音技术尤其是语音分析技术提供了新的解决思路。 一方面可以帮助语言学家分析和解释语音现象,另一方面也可以促进自然语言处理在语音信息处理方面的发展。 计算音系学的核心应用就是文语转换(Text-to-Speech,简称:TTS)和自动语音识别(Automatic Speech Recognition,简称:ASR)。 TTS 的核心任务是以文本中词的序列作为输入,产生声学波形作为输出。 ASR 的核心任务是以语音的声学波形作为输入,产生单词串作为输出。 语音自动处理的主要方法有:贝叶斯公式(Bayes formula)、噪声信道模型(Noisy Channel Model)、N 元语法(N-gram Grammar)、隐马尔可夫模型(Hidden Markov Model,简称:HMM)等,这些方法奠定了计算语言学包括计算音系学中各种统计方法的基础。 赵忠德等(2009:35)认为音系学家们经常被数据分析所困扰,很难从文本中获得并保存语料进行实证研究,对语料的分析也很难全部用手工进行。 因此,计算音系学的研究重点并不是为了将音系理论用在计算机上(也可能是计算分析的副产品),而是着重于音系学理论本身的更新和发展(Heinz,2011:140)。 国内有关计算语言学的研究日益进步,如俞士汶(1993)、袁毓林(2001)、刘颖(2002)、冯志伟(2011)等。 赵忠德等(2009)首次提出计算音系学这个分支学科,强调计算方法在音系分析中的重要地位。 赵忠德等(2011:339)认为当今计算音系学存在四个关键的延展领域:优选论、自动学习、语法与语音界面以及支持音系描写。 然而,对计算音系学的研究和认知都相对滞后。

1.2 计算音系学的研究主题和方向

计算音系学的研究领域十分广泛,具体包含语言理论与形式重建、实践应用、自动学习和计算音系学与语法和言语的交互四大部分(Bird,1994)。 计算音系学的实践和应用涉及语音识别、语音合成、语音处理和语音交互四个方面。 语言理论与形式重建是在已有理论上的更新,或在形式语法的基础上重新构建形式体系,进一步完善和创建更加合理有效的音系理论框架。 实践应用主要与自然语言处理、计算机程序研发息息相关,一方面可以帮助音系学家测试音系理论,另一方面对词库音系学、自主音段音系学、历时音系学等音系学领域的发展具有重要意义。 自动学习通过观察人类语言学习的过程,统计并分析数据,总结规律,建立形式模型,实现计算机的自动处理,为音系研究提供有效数据。 机器学习是自然语言处理中的重点和难点。 音系-句法交互和形式重建息息相关,语言研究者试图推进句法-语音和句法-音系之间的交互作用(赵永刚,2016:24),若某一音系理论同样适用于句法学和语义学,那也一定适用语法学,也有助形式语法的重建。 反过来,语法形式又可以作用于音系学,完善音系学理论。

计算音系学属于形式语言学的范畴,其模型建构和形式模拟都离不开音系学和计算机科学的跨学科发展。 第一,形式语言学、计算机理论与音系学理论之间的关系应该纳入计算音系学的研究之中。 音系学离不开形式化的方法,形式框架比较(如SPE 和OT)需要形式语言和逻辑之间的等价性,大规模约束模型的有效优化需要有限状态模式。 诸如标准化(unification)、谓词逻辑(predicate logic)、模态逻辑(modal logic)、类型理论(type theory)、分类语法或者逻辑(categorial grammar/logic)、有限状态模式(finite-state devices)、形式语言理论(formal language theory)等,都是建构理论与形式的重要参考。 第二,自然语言处理和自动语音识别(NLP/ASR)对计算音系具有重要影响。尽管语言处理领域不被视为计算音系学,但概率模型对自然语言问题具有很大的认知效用。 第三,自动学习模型依赖计算音系学的研究结果。 音系学的计算模型与语法和言语的计算模型相结合,可以模拟人类言语行为和语言习得的测试模型,以及为音系学家概括特定的有用数据。 例如,认知计算模型特别关注音系和音系组配习得的计算方法,以及婴儿和儿童对单词切分的习得。 第四,大规模语音数据处理与计算音系学的关系密切。 计算音系学的大部分工作依赖于语料库语言学方法论知识的共享体系,同样,几乎总是有必要对语料库进行预处理以满足特定语言研究的需求。 认知计算建模涉及语音数据语料库,或来自刺激“语料库”的行为结果,或两者兼而有之,如语音习得认知建模工作运用了有限状态OT(Hayes et al.,2008)。 以上所提的许多研究都借鉴了形式语言学理论的共同基础,大部分音系认知计算模型都集中在音系组配和音系学习领域。 基于约束的音系学习方法和对音系变异的随机方法都是有意义的(Daland,2014)。 计算音系学研究呈现出三种趋势:数据科学和模型比较、使用计算模拟对音系现象进行建模、以及用定理和证据表征音系模式的计算性质(Heinz et al., 2016)。 总之,计算音系学四大研究方向深入到了语音技术的各个领域,对自然语言的音系学研究有着重要作用。

2 计算音系学的主要研究方法

语言家在分析自然语言时,经常需要处理大规模语料,而人工分析耗时耗力,容易出错,造成实验结果不够客观。 面对这种情况,研究者在传统语言学分析的基础上,将计算方法与语料分析结合起来,形成了计算语言学。 早在20 世纪80 年代初,赫尔辛基大学计算语言学教授基默·寇斯克尼弥(Kimmo Koskenniemi)最先在分析芬兰语(后扩展至其他语言)时就提出了计算音系学与形态学的有限状态两级模式(Koskenniemi,1983;Kaplan et al.,1981)。 冯志伟早在1979 年便详细介绍了乔姆斯基(Chomsky)等形式语言学理论中语法的四种类型:有限状态语法、上下文无关语法、上下文有关语法和0 型语法,以及与之相应的四种自动机:有限自动机、后进先出自动机、线性有界自动机和图灵机(冯志伟,1979:34),对后来的计算语言学研究产生了重要影响。 计算音系学将数理计算方法和音系研究结合起来,主要有两大计算方法:有限状态模式(Finite-state Models)和联结主义方法(Connectionist Methods)(Bird,1995;赵忠德 等,2011:339)。

2.1 有限状态模式

有限状态模式主要指两级音系学(two-level phonology)这种模式,接近于经典音位学和SPE 音系学的方法。 有限状态模式最初应用于计算机、机械电子电路等,后推广至管理学、自然语言处理等领域,该方法同样适用于语言学研究。 现存的自然语言中,大多数语言(如英语)在言语表达上属于无限语言。 这些语言通过构词法或复杂句式,不断产出新的表达,具有强大的自我再生能力。 无限语言的研究不仅对计算语言学家意义重大,也对所有关心自然语言的人意义非凡(Borschev et al.,2004:2)。 语言的句法结构、音系结构等语法规则都可以用有限状态模式来研究,从而使无限状态语言模式化,将无限转化成有限,这一点和乔姆斯基的生成语法有异曲同工之妙。 乔姆斯基用形式化方法研究自然语言,利用数理逻辑对语言进行定义:给定一组符号(一般是有限多个),称为字母表,以∑表示,又以∑∗表示由∑中字母组成的所有语符列(或称字,也包括空句子和空符号串)的有限或者无限集合,∑∗的每个子集都是∑上的一个语言。 例如,若令∑为26 个拉丁字母加上空格和标点符号,则每个英语句子都是∑∗中的一个元素,所有合法的英语句子的集合是∑∗的一个子集,它构成一种语言(Chomsky,1956)。 道格拉斯·约翰逊(Douglas Johnson)(1972)很早就表明可以用有限状态均值对音系学的某些方面进行建模,罗纳德·开普兰等(Ronald M.Kaplan)(1981)则展示了一种将多个有限状态传感器编译成单个有限状态传感器,以实现SPE 风格的改写规则,该技术在开普兰等(1994)中有详细解释。

有限状态模式在音系学中主要应用在两个领域:音系改写规则(Phonological Rewrite Rules)(Johnson,1972)和两级规则(Two-level Rules)(Koskenniemi,1983)。 有限状态自动机(Finite State Automaton,FSA)为它们提供了计算支持。 FSA 又可具体划分为确定性FSA 和非确定性FSA。 确定性FSA 是指系统中由一个状态到另一个状态时的目的状态是确定的,而非确定FSA 中由一个状态转换到的目标状态是不确定的、可变化的。 其中,确定性有限状态转换器(Deterministic Finite State Transducer, DFST)形式化为七元组:＜q0,Q,F,Σ,δ,λ,Λ>①q0∈Q,q0 为初始态,Q 为状态的有限集合;F⊆Q,F 为终止态,是Q 的子集;Σ 为一组有限的输入符号(输入字母表);Λ 为一组有限的输出符号(输出字母表);δ 是Q×Σ→Q 中的函数,是转移集,它将一种状态和一个输入符号映射到另一种状态;λ 是Q×Σ→Λ 中的函数, 亦称转换函数(发射函数),它将一种状态和输入符号映射到输出符号。 这就准确描述了确定性有限状态转换器下输入到输出的过程。(Borschev et al.,2004:2)。 值得注意的是,FSA 只能进行状态间的变化,不能进行产出。 为了弥补这一不足,有限状态转换器应运而生,与自动机不同的是,有限状态转换器不仅能够改变状态,还可进行相应产出。 有限状态转换器不仅可以描述输入到输出的过程,还可以产出输出项(即表层结构)。 音系改写规则和两级规则是有限状态转换器最明显的两个应用。

两级规则(Two-level Rules)最早由寇斯克尼弥(Koskenniemi,1983)提出,用于建构计算机模型分析词形的认知和产出。 寇斯克尼弥构建了他的基于约束的模型,该模型不依赖于规则编译器、组合或任何其他有限状态算法,他称之为两级形态学。 寇斯克尼弥早先发明了一种用有限状态术语来描述音系交替的新方法。 与中间阶段的级联规则和它们导致的计算问题不同,规则可以被认为是直接约束词串表层的语句。 多个规则不会按顺序应用,而是并行应用。 每条规则都会限制某种词汇/表面对应,允许、要求或禁止相对应的环境。 他的两级形态学基于三个思想:规则是并行应用的符号到符号约束,而不是像改写规则那样按顺序应用;约束可以指词汇语境、表层语境或同时指两个语境;词汇查找和形态分析同时进行。 同样,一个复杂的音系规则通常包含多个子规则,底层形式每经过一个规则都会映射一个实际不存在的新词汇形式,直到形成最终的表层形式。 整个音系变化过程只需输入、输出和转换器三个组成成分。 有限状态转换器将音系底层形式作为输入形式,表层形式为输出形式,音系改写过程如图3 所示(Beesley et al.,1992:2):

图3 词汇形式-表层形式中的有限状态转换器

从图3 可以看出,有限状态转换器将多个规则组合成一个转换器,压缩成词汇形式(底层形式)到表层形式过程中的唯一规则。 此过程模拟了音系底层形式到表层形式的变化,极大简化了形态规则、音系规则等,降低了规则的复杂性。 两级模型与经典生成音系学的不同之处在于它提出了平行规则而不是连续规则。 这样就避免了单个词形派生过程中中间阶段的存在。 “两级模型”这个名称反映了这种设置,其中只有词法和表层“存在”,甚至在逻辑上也没有中间层。 OT 框架下的音系学家,对传统的有序改写规则进行了尖锐批判。 OT 理论就是一个两级理论,具有相似的并行制约条件,许多优选制约条件都可以简单地表示为两级规则。

2.1.1 音系改写规则中的有限状态模式

20 世纪60 年代形成的经典生成音系学理论,由一系列有序的改写规则(rewriting rules)组成,通过一系列推导过程将抽象的底层音系形式转换为表层语音形式(Chomsky et al., 1968)。 音系规则用来描述音系底层形式到表层形式的变化规律,是经典生成音系学的理论基础,通常用改写规则来表示。 音系改写规则通常与词汇形态变化形式相关,如φ→ψ/λ___ρ,其中φ 是替换的目标,ψ 是替换后的形式,λ 是替换目标的左边语境,ρ 是替换目标的右边语境,所有这四个成分都是常规表达式(Hetherington,2001:1)。 这个表达式和经典生成音系学中的改写规则“A→B/X___Y”一样,当A出现在X 和Y 之间的语境中时,A 要发生音变,变成B,也就是“XAY→XBY”。 自然语言中的现象通过形式化的规则,就成为音系的推导公式。 在计算音系学中,这些规则被称为语境敏感改写规则(Context-sensitive Rewrite Rules),它要比普通表达式或者语境自由改写规则(Context-free Rewrite Rules)更加强大。

有限状态转换器在音系改写规则中的应用十分普遍。 劳瑞·卡尔杜恩(Lauri Karttunen)(1998:3)以约克茨语①约克茨语(Yokuts):美洲土著人约克茨人所用的语言,以前主要居住在圣华金河谷南部和内华达山脉附近的山脚下,也可以称为Yawelmani 语。(Yokuts)为例,描述了该语言中元音交替的三个过程:圆唇化(rounding)、低音化(lowering)、缩短(shortening)。 当然,该语言里存在着共谋现象(Conspiracy)和绝对中和化(absolute neutralization)问题,很多学者都对此做过讨论,在此不做赘述。 以下以[ʔu:t+hIn]→[ʔothIn]为例,探究其中元音从输入到输出经历的三个步骤,如图4 所示:

图4 约克茨语中元音交替的改写三个过程②图4 和图5 中的符号“.o.”表示组合操作。

从图4 可以看出,[ʔu:t+hIn]→[ʔothIn]的过程经历了圆唇化、低音化、缩短三个步骤,[ʔu:thIn]首先经过圆唇化变成[ʔu:thun],再经过低音化变成[ʔo:thun],最后元音的长音缩短变成[ʔothun]。 约克茨语中的元音变化规则明显,顺序固定,适用于有限状态模式。 通过将三个规则合并可得到唯一转换器,如图5 所示:

图5 约克茨语中的元音交替的组合

通过对比约克茨语元音交替过程,可以发现,运用有限状态转换器下的元音变化更简洁清晰,实现了输入到输出的直接转换,减少中间环节,明显优于传统音系改写规则。 两级模型避免了非常有问题的规则排序,其作为过程模型之所以具有吸引力,也是因为它是基于有限状态自动机这种简单装置,它们可以通过多种网络和设备来实现。 总之,有限状态模式在音系改写规则上的应用十分普遍,有限状态转换器是对多个规则的合并,是在传统音系规则上的进一步创新。

2.1.2 有限元方法在两级规则上的应用

寇斯克尼弥最早于1983 年提出有限状态下的两级模型(Two-level Model)。 和音系的改写规则类似,两级规则也是生成音系学对音系底层形式到表层形式的描述。 这一理论最初用于芬兰语形态学的研究,后被广泛应用于各种自然语言。 该模型由三种形式(形态、词汇和表层表征)和两个与它们相关的规则系统(词库规则和音系规则)组成,如图6 所示:

图6 两级模型图

如图6 所示,该模型可以用有限状态转换器表示,并且易于实现。 事实上,该模型有两个方面:一方面它属于描述音系现象的形式主义方法,另一方面,它是一种计算装置,它将特定语言的描述为能够识别和生成词汇形式的操作系统。 两级规则的两级性指的是词汇层(lexical form)和表层(surface form)。 自然语言中经常会存在底层形式与表层形式不一致的情况,两级规则的出现就是为了合理解释这两个层级的差异现象(Koskenniemi et al.,1988:335)。 如3.1.1 中提到的约克茨语的元音交替过程也可以用两级规则来解释(Karttunen, 1998:3)。

与有限状态模式在音系改写规则中的应用相同的是:元音的圆唇化、低音化、缩短三个规则都被组合成一个有限状态转换器,降低了规则的复杂性。 不同的是,音系改写规则中,规则之间遵循严格的顺序,而两级规则中转换器内部规则之间处于平等地位,没有顺序性。 依据图7 所示的规则,约克茨语的圆唇化通过词汇环境的控制来实现,而低音化和缩短的共同影响则是[ʔu:t+hIn]中的u 变成了o。 因此,这三个规则之间不存在顺序性,每一个规则的使用和其对应的输入项无关,可单独构成一个大的规则。 这三个规则共同构建了一个有限状态转换器,再与输入联系起来。 因此,改写规则的基本计算操作是组合,涉及将规则应用于语符列以及合并规则本身;而对于两级规则,相应的操作是交叉组合和融合交叉。

图7 约克茨语元音交替中的两级规则图式

两级规则在其他语言中同样适用。 寇斯克尼弥等(1988:335)以芬兰语中“lasi”(意为“玻璃”)为例,分析了两级规则中的词汇形式和表层形式。 芬兰语中“玻璃”一词在表示“部分”的复数形式时,其词汇形式为“lasiIA”,这里“lasi”为词干,“I”为复数词尾,“A”为表示“部分”概念的词尾,而其复数的表层形式为“laseja”。 从“lasi”到“laseja”的变化,蕴含着三个变化,这三个变化可以分别用两级规则和音系改写规则分析如下:

(1)两级规则:i: e＜=＞___I:

音系改写规则:i→e/___I

芬兰语中“i”只有在后接复数后缀“I”时才会变成“e”。 如“lasi”进行单复数转化时,词干最后的“i”受到后面的“I”的影响变成了“e”。 即[lasiIA]→[laseIA],那么

(2)两级规则:I: j ＜=＞:V___:V

音系改写规则:I→j /V___V

芬兰语中,词缀“I”和词尾“A”都对应元音,根据(1)可知“I”前的音位“i”变成了“e”,“I”在两个元音之间变成了语素“j”,即[lasiIA]→[lasejA]。 由“A”到“a”的过程实际上是元音和谐的过程

(3)[A ∶a|O ∶o|U ∶u]=>∶Vback∶Vnonfront∗

最后一个音位严格遵守元音和谐规则,要求词尾元音和词干元音在前后特征上保持一致,因此,“A”受词根“e”[+前位性]特征的影响,变成了前元音“a”,即[lasejA]→[laseja],而中间的元音只要不是前元音,任何元音都可分布于此。 当然,规则(3)并不属于两级规则,因为输入输出之间并不是双向的。 从以上分析可以看出,芬兰语中词汇底层到表层的转变,同样可以利用有限状态模式来完成,通过将(1)、(2)两个两级规则组合起来形成一个有限状态转换器。

总之,从有限状态模式在音系改写规则和两级规则上的应用可以看出,它们对约克茨语的描述是相同的,都是从底层形式到表层形式的映射,只是从不同的角度将复杂的元音转换关系简化为更易理解操作的音系关系(Karttunen,1998:4)。 当然,基于经典音位学、弗斯(Firthian)音系学和自然生成音系学(所有这些都是陈述音系学方法),两种基于约束的方法都是通过音系规则约束引入,从而导致其分析与陈述音系学非常相似。 音系改写规则和两级规则的共同点是都以FSA 为计算基础,用于解释语言中的普遍联系。 音系改写规则中规则之间具有严格的顺序性,而两级规则中条件之间是对立平等的。 值得注意的是,音系改写规则中的各规则之间是垂直分布的,而双约束关系将满足相同语境的规则结合起来,形成平行的有限状态转换器。 也就是说,音系改写规则描述的是不同情境下的规则,且规则间存在顺序性。 两级规则适用于相同语境的规则集合,对顺序性没有要求。 同时,前者的核心在于组合,通过将规则顺序性连接起来形成有限状态转换器,而后者更关注规则之间的相互关系和相互影响。 综上所述,有限状态模式可以用来描述音系现象,通过规则组合而得到有限状态转换器,从而简化中间环节,对理解和优化音系规则具有重要意义。

2.2 联结主义方法

除有限状态模式外,联结主义方法(Connectionist Methods)也是计算音系学经常使用的一种研究手段。 这一理论认为“复杂的认知能力来自简单处理单位,即神经元之间的互动,像语言这样的复杂行为反应了这些神经网络的基本特点”,人类对行为和精神状态的理解都是基于对大脑神经元的认知(赵忠德 等,2011:367)。 联结主义方法也被称为平行分布处理方法,最初产生于发展心理学,在20 世纪80 年代成为一种流行的研究方法。 该方法主要用来解释人类行为出现的方式和原因,模拟人类认知习得、知识存储和信息提取,与认知科学紧密相关,广泛应用于语言学各个领域,如语言处理、语言感知等。 尽管联结主义方法在不同领域的应用各不相同,但都蕴含着认知科学中的“连接”思想。 知识起源的两种观点——先天遗传说和后天培养说——都与联结主义相关。 先天遗传说不仅是基因间相互作用的结果,还受外界环境的影响(Elman et al.,1996:xi)。 同样,后天习得的过程也会受到某些特定基因的影响。 因此,这两种观点并不是简单的对立关系,而是相互联系,共同作用。 联结主义倡议以许多相互联结且平行运作的单元所构成的网络,来仿真人类的信息处理过程(赵永刚,2012:38)。 联结主义方法的核心就是系统内部之间的相互联系,各个分子间相互刺激,从而共同维护系统的稳定性。

联结主义方法是一个由神经元和权重(weights)组成的复杂网络系统,核心是平行分布式处理(Parallel Distribution Processing)和浮现特征(Emergentism)(Elman et al.,1996:50)。 联结主义方法是一个非常复杂的网络系统,由两个基本元素组成:组成元素(也叫节点或单元,类似人造神经元)和元素间的加权关系(Elman et al.,1996)。 节点从输入中选择合适的元素,输入到下一个节点,传送刺激,构成完整网络系统。 由于元素间的加权关系不同,节点之间的关系也存在差异,部分节点联系紧密,部分节点间联系不大。 刺激从一个节点传递到另一个节点,两个节点的联系越紧密,传递的刺激越强,反之则越弱。 詹姆斯·麦克莱兰德(James McClelland)等(2009)提出自然语言处理实际是模拟大脑信息处理的过程,无数人造神经元共同组成网络系统,每个神经元再通过这个网络系统同时作用,将刺激传递下去。 大多数情况下,输出是多个刺激共同作用的结果。

正是因为人类的认知行为是刺激通过神经网络传递下去的,信息传递的方式就显得尤为重要。戴维·普拉特(Dawid Plaut)(1998:144)介绍了联结主义方法下的三种信息流方法:正反馈神经网络、重复反馈式神经网络和多模块神经网络。 它们分别反映了信息传递的三种方向。 其中,正反馈是神经系统网络最简单的结构,即刺激是从输入到输出的单向传递,方向固定,功能单一。 但实际上自然语言还受到时间、环境等其他多重因素的影响,因此这一理论也存在缺陷。 重复反馈式神经网络是更符合现实情况的信息流方法,它强调系统中神经元相互作用直到实现相对稳定的动态平衡。 丹尼斯·马雷沙尔(Denis Mareschal)(2003:32)通过对三四个月幼儿关注点的变化与表征构建的关系进行研究,总结出这一过程的联结神经网络,如图8 所示:

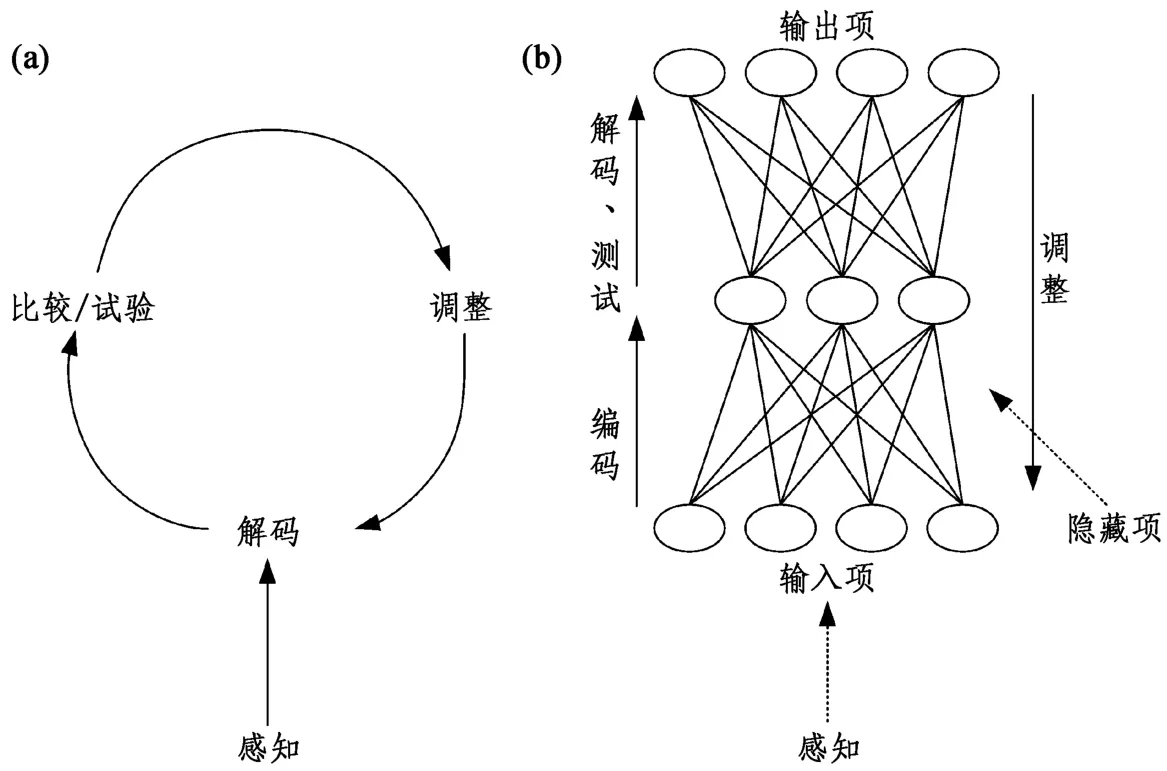
图8 婴儿对新信息感知过程及自动解码的神经网络

图8(a)表示婴儿对新信息的感知过程,图8(b)模拟了婴儿神经网络的自动解码过程。 该图主要反映了幼儿关注点变化过程,符合正反馈神经网络的特点。 假设幼儿先前接触过有关“猫”形象的输入,那么在同时接收到“猫”和“狗”的照片时,幼儿对狗的关注度会更高。 因为“狗”在这一情境下是新的输入,幼儿会对新信息投入更多关注,并对其解码处理,然后变成自己的内化知识。 从该实验中可以得出:幼儿对新信息表现出更大的兴趣,通过对新信息进行处理,内化成自身知识的一部分。 同时值得注意的是,幼儿吸取的知识往往是范畴化的知识,如在看到“狗”的形象时,不会仅仅是对特定的某一只狗的理解,而是对种群的整体认知。 所以下次再接收到另一只“狗”的形象时,尽管和之前的形象不同,但仍当作已有认知对待,不会投入更多关注。 该原理类似人类活动中的条件反射。 人类往往通过实践习得能力,通过对环境产生刺激进行反应,越陌生的刺激系统处理时间越长,相同或类似刺激需要的时间则较短。

联结主义方法还可以用来解释很多自然语音现象,如发音同化(Sound Assimilation)和元音和谐(Vowel Harmony)。 元音和谐作为一种常见的语言现象,通常是指一个单词中的所有元音相互影响,最终达到和谐状态,包含某些相同或者相似的特征。 以芬兰语(Finnish)中元音和谐现象为例,研究者通常利用两级规则分析芬兰语中的元音和谐现象,并将其划分为两个平行条件,指出芬兰语词干中的最后一个元音会影响后缀元音的选择。 乔治·莱考夫(George Lakoff)(1988)讨论了音系过程中的三层表征:底层形式的形态音位层(morphophonemic level)、音位层(phonemic Level)和表层形式的语音层(phonetic level),并指出这三个层次之间为正反馈关系。 安尼莉·提卡拉(Anneli Tikkala)基于神经网络系统,提出一种名为FinnPro 的研究工具,建立交互刺激传递模型(Interactive Spreading Activation Models)和模拟词汇产出过程(Word Production Process),研究芬兰语中的元音和谐现象,该原理类似人类活动中的条件反射。 和有限状态模式不同的是,提卡拉首次利用神经网络来研究芬兰语中的元音和谐现象。 这种网络系统又包含选择网络(Selection Network)和控制网络(Control Network)两个子系统。 芬兰语中包含八种元音,根据元音和谐规则,可将其分为三类:前元音、后元音和中元音。 其中,前元音和后元音属于和谐元音。 芬兰语中存在两种元音和谐现象,一种是词干中的元音和谐,一种是在给词干添加词缀时产生的后缀和谐。 图9 是提卡拉从神经网络的角度分析了芬兰语中元音和谐的原理。

图9 芬兰语中的元音和谐的神经网络系统

如图9 所示,利用FinnPro 工具所研究的元音和谐过程,明确将音节层和音位层分隔开来。 这一系统下的元音和谐受四个节点控制:刺激前节点和终止前节点、刺激后节点和终止后节点。 如图所示,实线代表刺激传递的方向,虚线代表终止。 箭头表示刺激传递的方向。 刺激前节点激活所有前元音:/y ä ö/,刺激后节点激活所有后元音:/u a o/,它们同时也可以反过来刺激自身。 元音之间相互抑制。 刺激前节点将刺激传递到终止前节点,刺激后节点传递刺激至终止后节点。 终止前节点抑制终止后节点和任何包含后元音的音节核的产生。 反过来,终止后节点也会抑制终止前节点和任何包含前元音音节核的产生。 节点与节点之间相互作用,互为掣肘。

综上所述,自然语言的音系结构十分复杂,受到多种制约条件的限制,很难用经典音系学中简单的形式化规则来描述音系变化过程。 联结主义方法为语言分析提供了计算机模拟的支持,也构建了音系本质研究的计算基础(Touretzky et al.,1989:372)。 当然,架构联结机制模型,分析音位在多个位置的同时插入、删除、突变等现象,对分析音系现象也极具开创性。

3 计算音系学发展现状

3.1 国外计算音系学发展现状

随着人工智能的发展,计算音系学开始引起广泛关注,语音技术也成为学界关注的热点。 当前国内外计算语言学发展迅猛,计算音系学作为计算语言学的一个分支,理应得到足够重视。 国际计算语言学协会计算音系学特别研究小组(ACL Special Interest Group in Computational Phonology,简称:SIGPHON)于1991 年成立,专注于计算音系学的研究。 整体来看,国际上有关计算语言学的成果较多,但专门针对计算音系学的研究成果依然较少。 随着自然信息处理和人工智能的发展,计算音系学必将成为研究的重点领域。

国外语言研究者往往将计算音系学与语言现象结合起来,以两种研究方法为核心的音系学研究方法,探究其跨学科功能。 尤其是在自动学习和语音交互上,如优选论在音系规则中的功能、联结主义方法在语言处理中的应用等。 计算音系学发展初期,海外研究者汲取各领域的知识,迎来了理论发展的高潮期,相关理论蓬勃发展(Johnson,1972;Elman et al.,1996;Bird,1994;Plaut,1998)。伯德(1995)指出了计算音系学的两大研究方法:有限状态模式和联结主义方法。 基础框架构建之后,学术研究者开始将目光转向理论在自然语言现象中的具体应用(Karttunen,1998;Koskenniemi et al.,1988;Hetherington,2001)。 与此同时,还有一些跨学科学者通过建立模型来模拟语言产出过程(Tikkala,2000;Mareschal,2003)。 尽管计算音系学的发展已经有了一段时间的历史,但整体还处于学科发展的建设阶段。

目前,进行计算语言学研究的国家主要有美国、英国、德国等。 美国的语言学研究一直位居世界前列,除了传统语言学专业,美国大学还非常注重语言学和其他专业结合产生的交叉学科,如计算语言学、心理语言学、神经语言学等。 其中,这些大学开设的计算语言学专业通常是有计算机系和语言学系联合培养,如斯坦福大学、宾夕法尼亚大学、芝加哥大学、爱丁堡大学等;大多数大学都将这一专业设置在计算机或工程学院下,少数学校的语言学系也有这一专业。 开设语音处理相关专业更是寥寥无几,英国爱丁堡大学的语音与语言处理专业(MSc Speech and Language Processing)在国际上较为有名。

3.2 国内计算音系学发展现状

与国外相比,国内在计算音系学领域的探索相对较少,且集中在二语习得领域,与自然语言现象的结合并不是很多。 国内有限状态模式主要应用在自然语言处理方面,而联结主义的探索较为普遍。 葛鲁嘉(1994)第一次提到联结主义研究方法,指出这一手段在认知科学上的重要性。 后来的研究者逐步将联结主义应用在语言学上,特别是二语习得。 杨剑峰和舒华(2008)通过研究英语词汇阅读的平行分布方法是否同样适用于汉字阅读,得出中英文具有普遍的加工机制。 值得注意的是,和乔姆斯基不同的是,联结主义方法主张规则不具有先天性,而是“基于对大量输入语料的统计学习而浮现出来的特征”。 王迈(2015)在前人研究的基础上,较为全面地将联结主义的主要特征总结为:节点、关系、并行、容错性、自动学习、遗忘和规则浮现。 同时指出对无限集的分类是以破坏细节特征规则为代价的,并不是最好的选择,这是进行联结主义分析时需要注意的问题。 柴春丽(2010)指出语感是联结主义方法的一个典型应用,正是由于输入的一次次重复,刺激了神经网络系统,才促使了权重的增加,熟练是学习的表面产物。 尽管频率对语言习得其至关重要的作用,周昱(2014)却强调频率并不是决定性的唯一条件,如二语学习者接触英语冠词的频率最高,但掌握顺序却靠后。

整体来看,现阶段国内使用计算方法分析或者模拟音系现象研究还不是很多。 一方面,国内语言学研究者更偏向语言本体的研究,提到计算往往都望而却步,语言学学者缺乏计算机、数学背景,在这一领域的研究中受到局限。 另一方面,尽管硕士阶段国内开设语言学专业的院校非常多,但研究理论语言学的学者相较较少,基于学习难度和就业需要,可以开设这个专业方向的高校寥寥无几,学生更多偏向应用语言学领域。 过去,语音相关研究基本都是计算机专业的人在做,随着自然语言处理、人工智能、机器翻译等领域遭遇瓶颈,研究者发现计算机科学家并不能解决所有语言问题,这一领域需要语言学家的参与。 目前,越来越多的公司开始招募语言学专业的人才,如谷歌、讯飞等科技公司。 面对计算语言学发展的“黄金时期”,叶子(2017)提出高校语言学专业人才培养需要进行两方面转变:“首先,语言学基础学科,如音系学、句法学、语义学等应当加大形式化描述的比例,要让学生在语言学实例中感受数学模型的运用。 其次,要加大基础课程中数学学科的分量。 对语言学来说,由于支撑核心的句法语义现象的数学主要是离散数学,因此有必要将这门课程作为重点课程。”

4 结语

综上所述,本文通过概述计算音系学基本定义、分析其两大主要研究方法的具体应用、国内外培养现状,旨在系统介绍这一学科,让读者初步了解计算音系学这一领域。 计算音系学作为计算语言学下的一个分支,利用计算方法来研究音系学中遇到的问题,与自然语言处理相得益彰。 计算方法的利用可以在很大程度上系统化、模式化语音产出和感知的过程,降低语音研究者的时间成本。同时也应该看到,计算机遵循指令而不会做出判断,虽然非常擅长评估语法的一致性和描述的充分性,但除非程序员提供必要的信息(即衡量由语法分配给字符串结构准确性的标准),否则他们无法测试解释充分性。 总之,在智能化快速发展的新时代,语言学家应当转换自己的身份,积极参与并融合其他学科最新发展,共同推进人类语言知识的更新与进步。 人工智能是新时代的创新,人类对人工智能既有向往又有敬畏。 事实上,该研究的意义在于提高人类生活的智能化,给人类提供生产或者生活的便利,而不是完全取代人类大脑,解放人类双手。 语音输入、语音识别技术的开发,也可以进一步推进生产和生活的智能化,提高人类的生活质量。