冲击荷载下配筋率对泵站框架梁动力响应的影响

张玉民，陆 亮

(山东润泰水利工程有限公司，山东 泰安 271000)

钢筋混凝土梁结构是工民建中常用的工程结构。既有研究表明，混凝土和材料和钢筋均属于典型的率相关材料，在爆炸和冲击荷载作用下，结构的动力响应和静载作用下有显著的区别。通常率相关材料的强度会随加载速率的增大而显著提高。罗绪昌等[1]基于ABAQUS数值模拟系统的研究了钢筋混凝土深梁在冲击荷载作用下的动力响应。结果表明，梁的塑性发展程度随加载速度的增大而增大，随混凝土强度的提高，梁沿长度方向的剪力显著增大。赵武超和钱江[2]综合采用物理模型试验和数值模拟分析了混凝土梁在冲击荷载下的局部响应特征，结果表明，惯性力和负向支座反力均会影响梁体局部响应阶段。付应乾和董新龙[3]基于1∶1模型试验分析了落锤冲击下钢筋混凝土梁的破坏形态，结果表明，低速冲击下，梁的破坏表现为弯曲破坏，高速冲击下，梁的破坏由弯曲破坏转变为剪切破坏。许斌和曾翔[4]基于室内冲击试验，研究了动荷载下钢筋混凝土梁的破坏形式，结果表明，惯性力会梁的剪力分布发生，并在此基础上给出了估算梁承载能力的计算方法。易伟建和史先达[5]基于能量等效原理，分析了冲击荷载下钢筋混凝土剪力墙动力响应行为，结果表明，冲击能量和墙中最大位移成线性增长；当轴压比小于0.3时，轴力对结构的抗冲击能力有利，小轴压比情况下可以不考虑轴力进行设计。

目前的相关研究主要集中于冲击荷载作用下梁的破坏形式。实际工程中，由于设计荷载及结构形式的不同，梁的配筋率均会有所差异，不同配筋率对钢筋混凝土梁的动力响应行为研究较少。基于目前研究的不足，本文采用ABAQUS数值软件建立计算模型，系统的研究了不同配筋率和不同加载速度对梁的破坏形式的影响。本文的研究可为钢筋混凝土梁在动力作用下的设计和加固提供参考。

1 有限元模型及计算参数

1.1 模型建立

建立典型钢筋混凝土梁计算模型如图1所示。梁的长度为1.0m，截面尺寸为0.1m×0.1m，纵向受力钢筋采用HRB335φ10钢筋，箍筋采用HRB335φ8@50钢筋。混凝土保护层厚度为20mm。

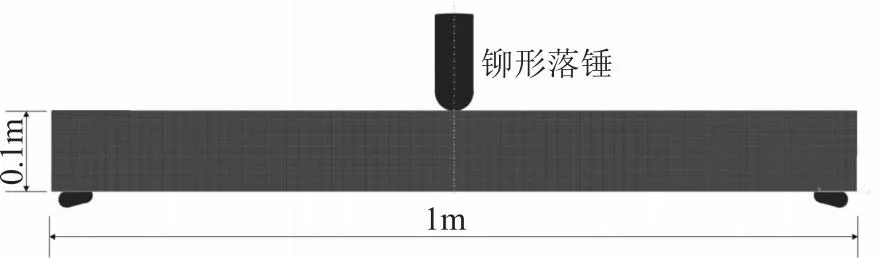
图1 数值计算模型

试验采用的钢筋混凝土梁加载器为典型的铆形重锤。通过改变锤头几何尺寸和增大密度可以保持落石的冲击能量不发生改变。数值模拟中，锤头与钢筋混凝土梁上表面的接触设置为面面接触。混凝土和锤头网格采用C3D8R减缩单元，钢筋采用truss单元模拟。加载速度分别为4.9、6.9和9.8m/s。模型最终的网格总数为135310，节点个数为146120。

1.2 计算参数

既有研究表明，混凝土材料和钢筋采用均属于典型的率相关材料。为充分考虑结构加载速率对材料力学响应的差异性。针对混凝土材料本位采用混凝土塑性损伤本构(CDP损伤本构)。该本构通过定义损伤因子描述混凝土在动力作用下材料的损伤和劣化，可以较好的模拟混凝土在冲击爆炸荷载下的力学响应。混凝土的计算参数见表1。受压和受拉损伤因子如图2所示。

表1 混凝土材料参数

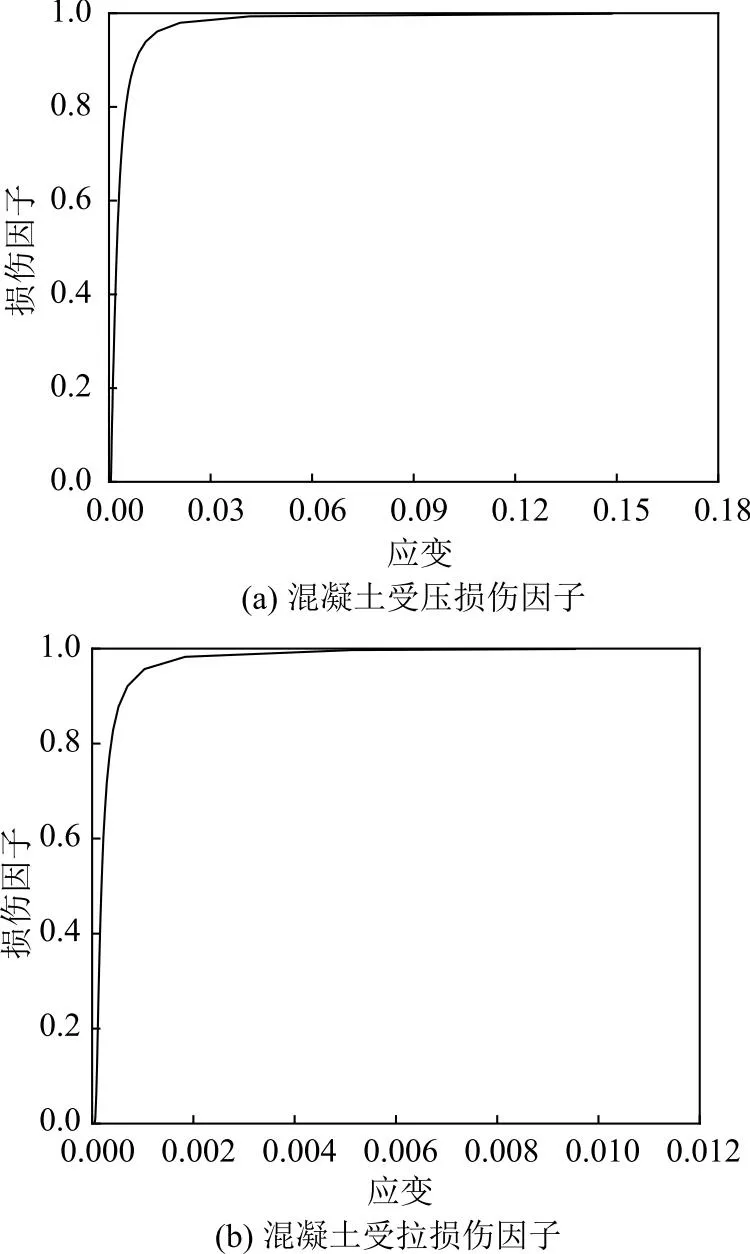
图2 混凝土损伤因子

为考虑钢筋材料的率相关性，本文使用三折线模型，根据林峰等[6]的研究，在不同的应变率下，钢筋的杨氏模量基本一致，钢筋的屈服强度和极限强度随应变率的变化规律为：

(1)

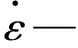
本文试验中HRB335钢筋参数见表2。

表2 钢筋材料参数

2 计算结果与分析

2.1 配筋率对冲击力的影响

3种不同配筋率对落锤冲击力的影响如图3所示。结果表明，3种配筋率下落锤的冲击力时程曲线均表现出先迅速增大随后减小最后平稳的过程。对应梁的变形为压缩加载和回弹典型阶段。3种配筋率工况下，落石的最大冲击力随配筋率的增大而增大，这是因为配筋率增大对应钢筋混凝土梁的有效刚度增大，从而导致落锤的冲击力增大。以冲击速度为4.9m/s为例，当钢筋混凝土梁的配筋率由2.57%增大至2.67%时，落锤的最大冲击力由147kN增大至159kN，增大比例为8.2%。当钢筋混凝土梁的配筋率由2.67%增大至2.78%时，落锤的最大冲击力由159kN增大至209kN，增大比例为31%。总体来看，随钢筋配筋率的增大，梁的承载力明显提高。随着冲击速度的增大梁的变形模式由弯曲变形逐渐向剪切变形转变。

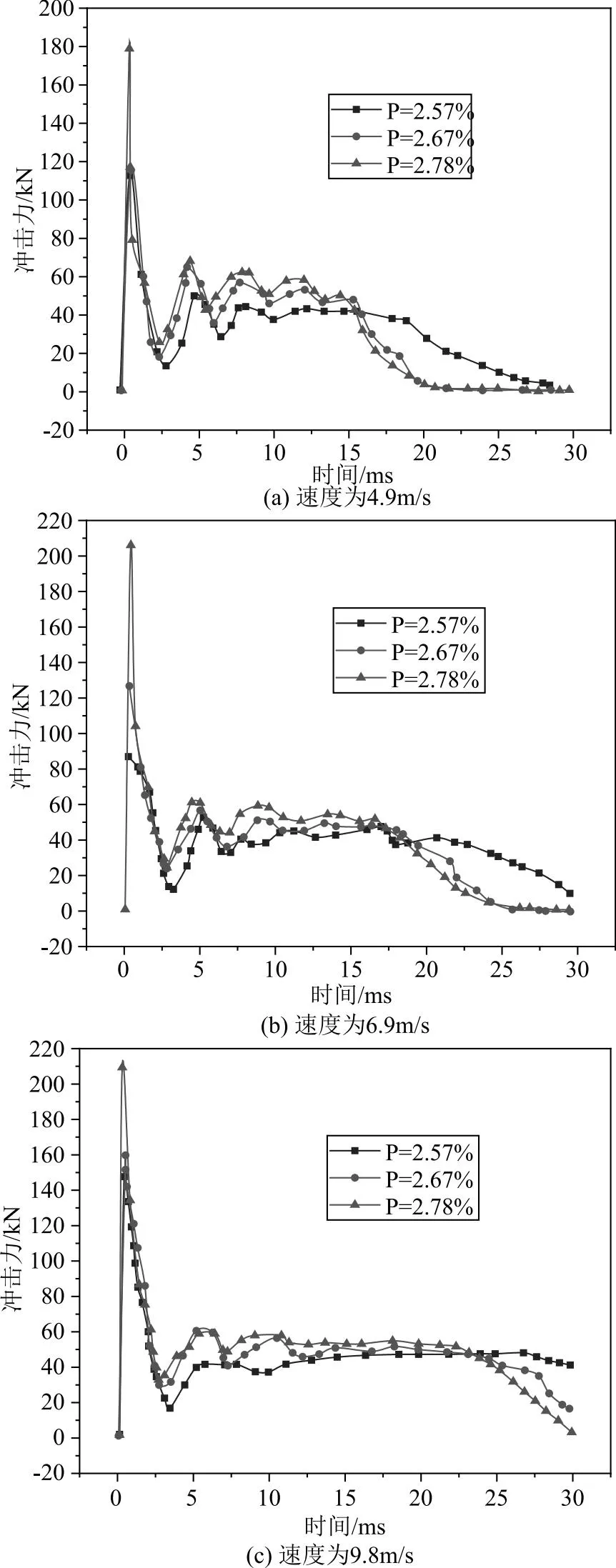
图3 配筋率对落锤冲击力的影响

混凝土梁在不同加载速度下的变形模式如图4所示。结果表明，混凝土梁的变形裂缝首先由梁跨中开始发生，随冲击力的增大，梁的裂缝逐渐扩展贯通，随冲击速度的增大，梁的挠曲变形显著增大，当速度较小时，梁主要表现为弯曲破坏，当速度较大时，梁的变形主要以剪切变形为主。

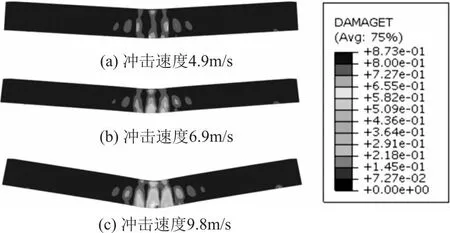
图4 混凝土损伤变形模式

2.2 配筋率对梁跨中位移影响

钢筋混凝土梁跨中位移变化规律如图5所示。

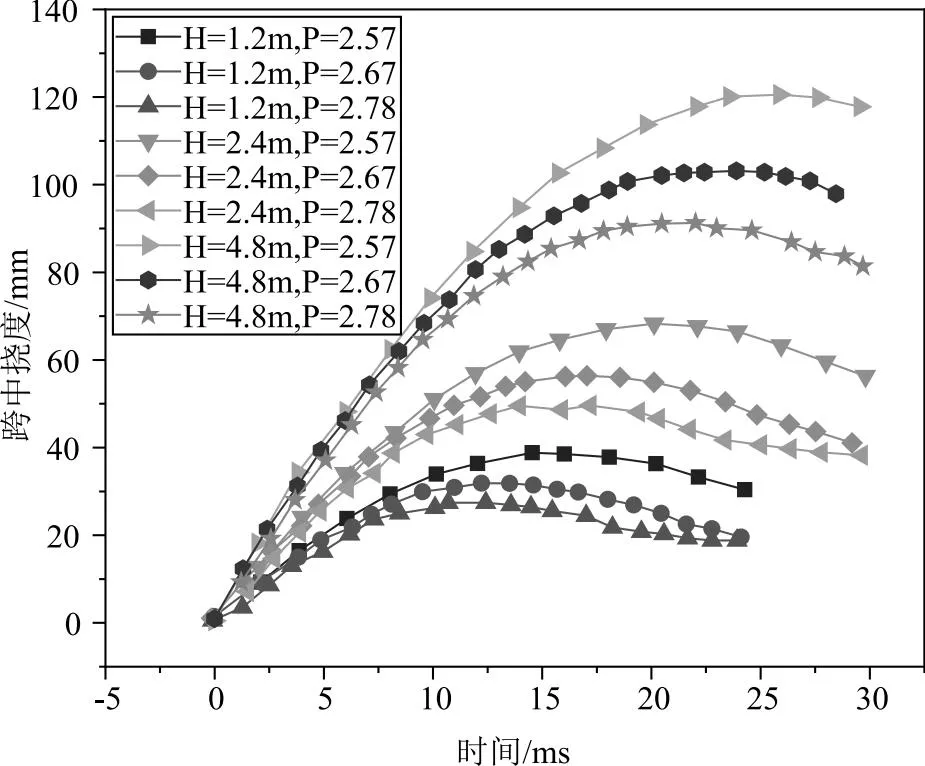
图5 钢筋混凝土梁跨中位移规律

结果表明，不同冲击速度及不同配筋率下，梁的跨中位移时程曲线表现出相同的趋势。随时间的增大，梁跨中位移迅速增大，随后保持稳定。在不同冲击速度及不同配筋率下，钢筋混凝土梁稳定时对应的位移为梁不可恢复塑性变形。在冲击速度为4.9m/s和配筋率为2.57%时，梁的最大变形和塑性变形为38.8和30.3mm。在冲击速度为4.9m/s和配筋率为2.67%时，梁的最大变形和塑性变形为31.8和20.5mm。在冲击速度为4.9m/s和配筋率为2.78%时，梁的最大变形和塑性变形为27.4和18.7mm；在冲击速度为6.9m/s和配筋率为2.57%时，梁的最大变形和塑性变形为68.3和56.3mm。在冲击速度为4.9m/s、配筋率为2.67%时，梁的最大变形和塑性变形为56.3和241.0mm。在冲击速度为4.9m/s和配筋率为2.78%时，梁的最大变形和塑性变形为49.6和38mm；在冲击速度为4.9m/s和配筋率为2.57%时，梁的最大变形和塑性变形为120.5和117.2mm。在冲击速度为4.9m/s和配筋率为2.67%时，梁的最大变形和塑性变形为103.1和97.8mm。在冲击速度为4.9m/s和配筋率为2.78%时，梁的最大变形和塑性变形分别为91.2和81.3mm。显然，相同冲击速度下，随配筋率的增大，跨中最大挠度和最终塑性变形均显著减小，梁的抗变形能力随梁配筋率的增大而提高[7]。

2.3 配筋率对梁破坏模式的影响

汇总得到钢筋混凝土梁的加载-位移。结果表明，不同冲击速度和配筋率下，梁的冲击力-变形曲线表现出相同的趋势。在梁的压缩阶段，跨中位移随冲击力的增大而增大，在梁反弹阶段，梁的位移随冲击减小而减小。达到稳定时，梁的变形为不可恢复塑性变形。以冲击速度4.9m/s为例，在3种不同配筋率工况下，落锤冲击力随跨中挠度增大而呈波动变化趋势。可见，梁在冲击荷载下，发生反复的压缩和回弹，表现出弯曲变形趋势。增大冲击速度至6.9m/s时，在最小配筋率工况下，梁在跨中位移最大值达到40mm时逐渐稳定，此时梁的变形逐渐由弯曲变形转变为剪切变形，而其他2种配筋率较大的梁仍然表现为弯曲变形。继续增大落锤速度至9.8m/s时，除配筋率为2.78%的梁表现为弯曲变形以外，其他两种配筋率的梁均表现出典型的剪切变形的特征。总体来看，随配筋率的减小，梁在动荷载作用下发生剪切破坏的概率在增大。

3 结语

基于数值模拟开展泵站框架结构梁在动荷载作用下的动力响应，得到如下结论。

(1)不同配筋率下，落锤的冲击力时程曲线均表现出先迅速增大随后减小最后平稳的过程。增大梁的配筋率，可以提高梁的承载力。此外，随冲击速度的增大，梁由弯曲变形逐渐向剪切变形转变。

(2)混凝土梁的裂缝首先由跨中开始，随着冲击力的增大，梁的裂缝逐渐扩展贯通，梁的挠曲变形显著增大。速度较小时，梁主要表现为弯曲破坏，速度较大时，变形以剪切变形为主。

(3)落锤的冲击速度相同时，梁的抗冲及抗变形能力均有所提高，冲击速度大于临界速度时，进一步增大冲击速度，配筋率对梁的抗变形能力的影响不再显著。