常用投影大地线的高效展绘及Mathematica实现
周东权,刘 敏,魏 冲,边少锋,张思远
常用投影大地线的高效展绘及Mathematica实现
周东权1,刘 敏2,魏 冲3,边少锋1,张思远1
(1 中国地质大学(武汉)地质探测与评估教育部重点实验室,武汉 430074;2 中国人民解放军91001部队,北京 100830;3 中国人民解放军92823部队,三亚 572000)
针对大地线方程的复杂性及高效展绘难以实现的问题,以第三扁率改化大地问题正反解的计算公式,根据法截线方位角与大地方位角的数学关系提高大地方位角计算精度,并提出了等间距内插的大地线展绘方法;利用Mathematica建立了精度自适应控制模型,提高了等间距内插的效率和精度;利用Mathematica强大的绘图功能实现了不同距离和应用场景下不同地图投影的大地线展绘,挖掘了大地线展绘的应用价值。实验结果表明:该方法在精度可控的条件下能实现对任意长度大地线的高效率展绘,不同地图投影的大地线展绘在不同的应用场景下具有独特的意义。
第三扁率;Mathematica;大地线展绘;等间距内插;自适应控制模型
0 引言
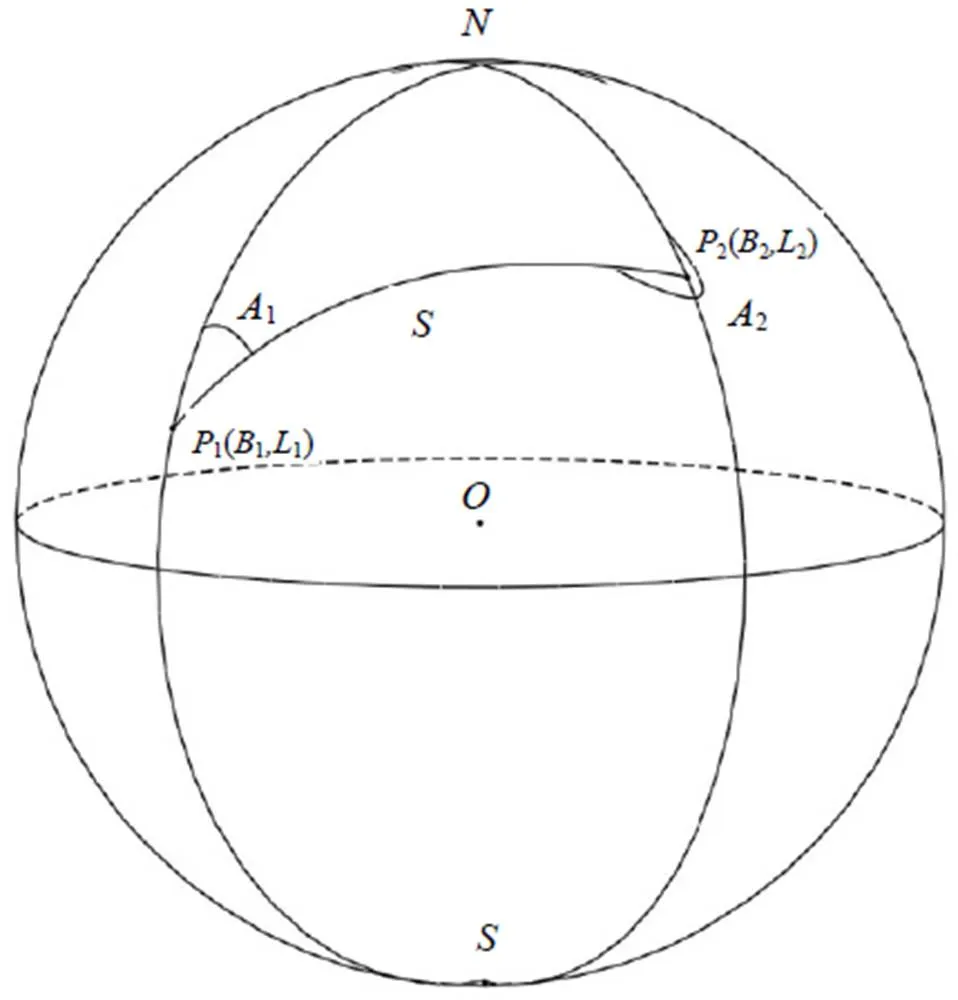
图1 大地主题解算示意图
随着计算机代数系统的不断发展,大地主题解算的精度和效率也得到了提升[3-4]。与传统的研究不同的是,计算机代数系统对大地解算公式进行了系统的革新,并能创新性地讨论贝塞尔大地解算等传统思路的新方法,简化了大地主题正反解的公式,并提高效率[5-6]。同时符号计算的出现也能够针对过往大地问题研究中缺乏考虑的问题,在建立新的参考椭球的基础上,提出新的大地问题解算方法,如顾及高程的大地问题解算方法[7-8]。大地问题解算算法的不断完善,为大地线的高精度展绘提供了算法基础[9-10]。
大地线由于本质是一条空间曲面曲线,与平面曲线的绘制不同,函数方程复杂,需要综合解算的方法来实现展绘[11-12]。“以直代曲”是大地线展绘的常见方法,即通过大地解算,得到大地线上一系列密集的点位,通过点与点的连接实现大地线的展绘。为此,相关学者在该思路的基础上,提出了大地线的内插方法,根据地球曲率计算最大插值间隔,建立绝对精度阈值约束的内插算法,提高了大地线的绝对精度,却由于过多的内插点降低了大地线的展绘效率[13]。针对大地线展绘算法中内插参数与精度自适应匹配的问题,学者建立了大地线展绘长度误差与拱高误差的定量评估模型,提出了一种有效控制阈值的快速展绘算法。由于现有大地线展绘方法大多建立于大地线方程在投影中的精确表达,继而建立的矢量数据模型[14],形式单一,往往建立在墨卡托投影等角和固定比例尺的条件下,无法满足许多场景的应用。
Mathematica是基础研究、应用基础研究以及工程技术领域流行的计算机代数系统[15-16],在参考椭球数学计算分析、微分几何分析、地图投影和数据归上有着系统的强大的数学分析能力、符号推导能力和可视化能力,具有便捷快速地建立任意投影的强大能力。基于此,本文在改化公式的基础上,利用Mathematica建立大地线展绘算法,实现大地线在常用投影的高效展绘,挖掘可视化技术在大地测量学的应用价值。
1 算法的基本原理

图2 算法流程图
在计算得出各个点的大地坐标后,同时可以得出各点的空间坐标,利用Mathematica的强大内核,完成在不同投影的展绘。
2 大地主题解算
2.1 大地线长S计算

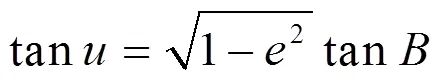
球面归化纬度与球面大圆弧长的数学关系式如式(3)所示
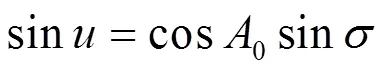
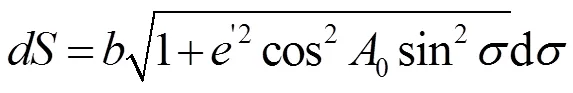

则
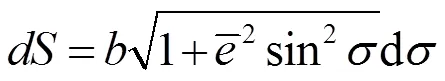
根据牛顿二项式展开定理的推广,可进一步展开,如式(7)所示


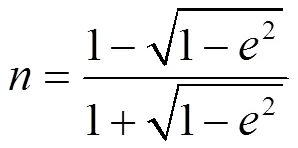
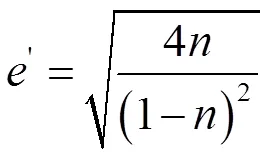

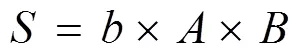
式中:

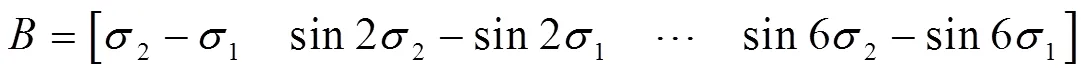
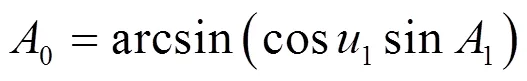
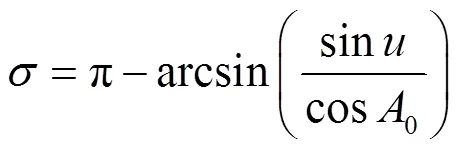
2.2 大地方位角计算及修正
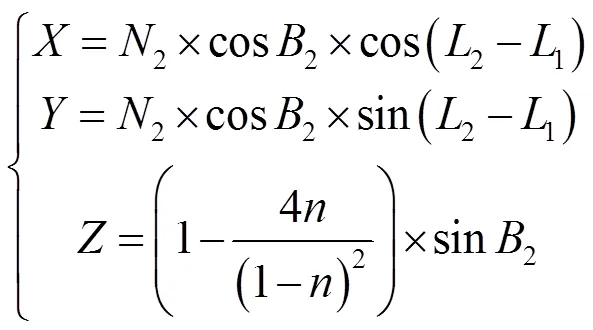
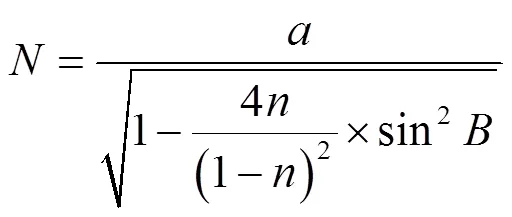



2.3 基于Mathematica的语法设计
Mathematica有强大的符号计算功能和制图能力,可以利用简洁的语言设计大地主题正反解计算的代数分析,如在大地方位角计算及修正等复杂的公式中,Mathematica能利用简单的语句设计,实现两点间大地坐标相关函数的计算。在计算过程中,与Matlab、Python等数值计算分析编程语言相比,Mathematica只需要最简单的函数自定义,即可将代数计算中复杂代数关系进行关联,从而实现复杂的代数推导及结果输出,涉及多元矩阵等计算时,代数系统能在操作页面建立并识别矩阵,与数值计算工具相比,更加简单便捷。其计算精度之高对于大地线的推导、改化和模型构建都提供了重大帮助。同时,Mathematica还能利用简单的语言建立复杂的地图投影,并实现自定义设计地图投影。对于Matlab、Python等数值分析语言,自定义地图投影需要复杂的嵌套函数以及程序设计,而在代数系统上,能利用内置的强大的数学工具及投影函数,对常用投影如Mercator投影,能够一句代码实现地图投影的建立,自定义参数的任意设定,同时能过通过代数推导,并利用Mathematica强大的绘图能力,实现自定义地图投影的建立,是大地线代数推导及展绘实现的坚实基础。
2.4 精度自适应控制模型
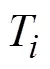
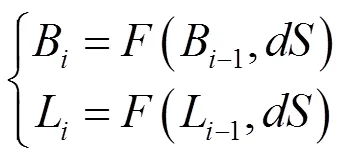
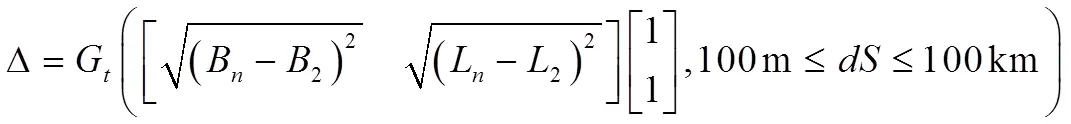
3 结果分析
3.1 大地线在空间直角坐标下的展绘
根据上述算法描述、内插方法和绘制要求,通过Mathematica12.0作为测试环境,分别对不同实验数据进行了大地线展绘实验,实验中所使用的参考椭球为克拉索夫斯基椭球,实验数据如表1所示。

表1 大地线展绘实验数据
大地方位角可从上述大地方位角计算及修正方法得出,即大地经纬度的变化会带动平行圈的变化,从而带动大地方位角的变化,因此大地线的展绘精度与两点大地经纬度以及大地方位角有关。三个算例的实验结果如表2所示,从中可以获知,算例2中大地方位角大,同时由于在大地线的展绘过程中,随着纬度的增加,大地方位角的减少幅度也在不断增加,会对展绘精度造成一定的影响。 算例3中,由于大地线的展绘从南半球到北半球展绘的过程中经过,大地方位角也由逐步变小到逐步变大,因此在展绘的过程中精度也在波动变化。
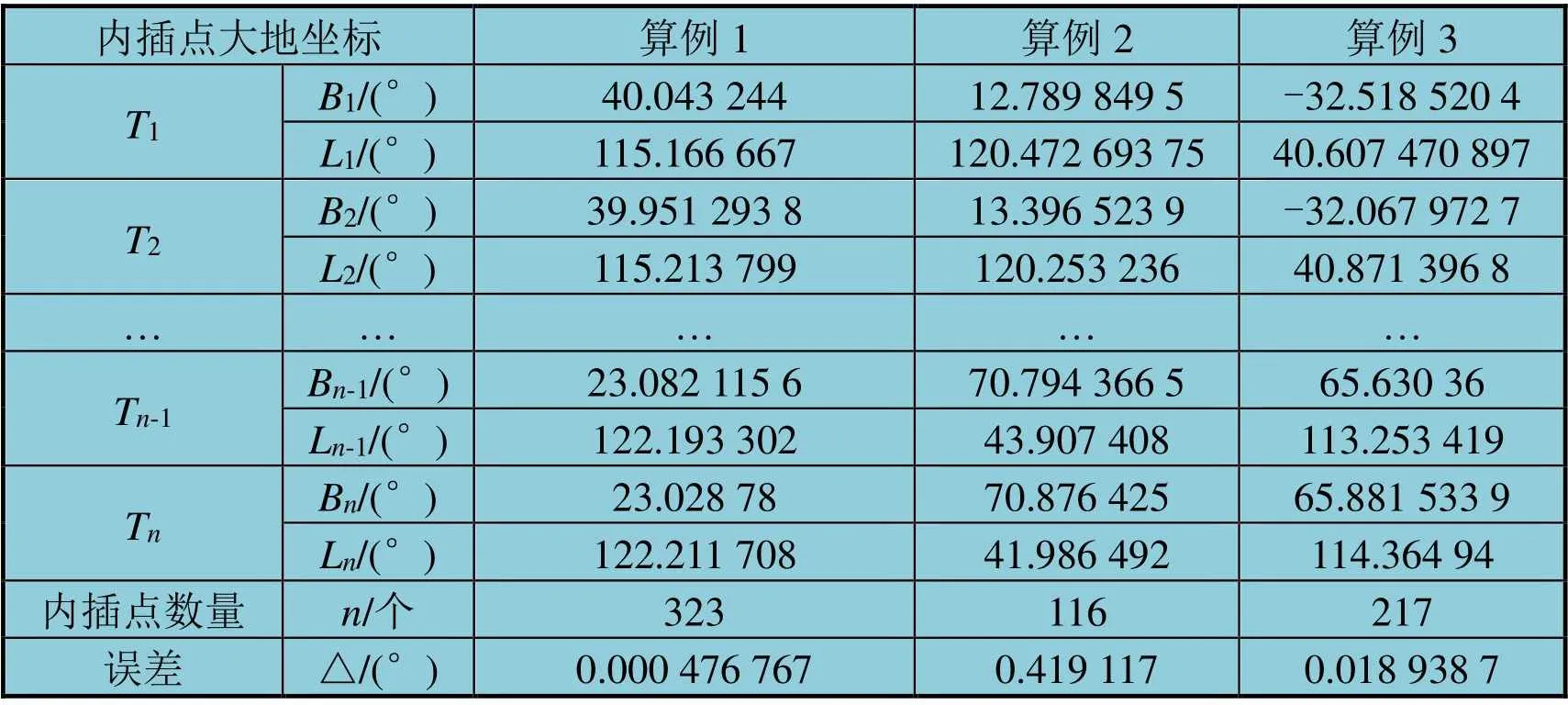
表2 大地线线展绘实验结果
此次展绘的实验结果还表明精度自适应控制模型根据大地线的展绘情况,选择了满足精度的内插间距,且满足了大地线绘制高效率的要求,同时可以得知,大地线展绘过程中,内插点数量与大地线长无关。总的来说,大地线的内插过程中大地方位角变化幅度越小,其展绘精度越高,三个算例的误差计算结果如图3所示,可以看出,算例1两点位于中低纬度,因此在51次的自适应调整中,精度都能保持较好,而算例2由于是从低纬度向高纬度展绘,而且终点纬度较高,精度较低,且精度变化较大。算例3由于是从南半球向北半球进行展绘,自适应模型随着调整次数的增多,即内插距离的逐步增大,精度得到了较好地调整,基本能满足展绘要求。理论条件下,算例2和算例3由终点向起点进行展绘能够得到精度更高的展绘结果,尽管如此,在精度自适应控制模型的调整下,都在满足条件的情况下实现了大地线高效率的展绘,这在未来大地问题的解算中,以及大地问题可视化算法进一步优化上,都具有一定的作用。

图3 精度自适应误差计算结果
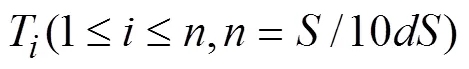

图4 内插点空间三维散点图
3.2 大地线在常用投影下的展绘
大地线是地球椭球体表面一条空间曲面曲线,在辨识和使用时往往要将其投影在地图上,其是一个曲面向平面投影的过程,不同的数学映射关系会构成性质不同的投影,按变形性质主要分为等距投影、等角投影、等积投影和任意投影。由于应用场景不同,往往采用不同的地图投影,地图投影的不同会影响大地线的展绘及使用。本文在不同场景的地图投影下对大地线进行了展绘,探究其特性。
Mercator投影是正轴等角圆柱投影,其没有角度变形,恒向线在其投影上表现为一条直线。三个算例在Mercator投影上的展绘如图5所示,蓝色为大地线,绿色为恒向线。通过三个算例在Mercator投影上的绘制可以得知:Mercator投影在两极变形大,在低纬度地区变形小,算例1大地线距离较短,大地方位角变化也不大,同时位于较低纬度,经差也较小,其投影变形小,因此在地图上近似为恒向线。而算例2和算例3距离远,大地方位角变化大,算例3大地线还跨越南北半球,投影变形大,可以看出与恒向线具有较大差别。总的来说,大地线在地图上展绘的表现形式受到地图投影变形以及大地方位角的影响,大地线与恒向线的关系和性质在船舶大洋航行、精确制导等场景应用中具有一定的意义。
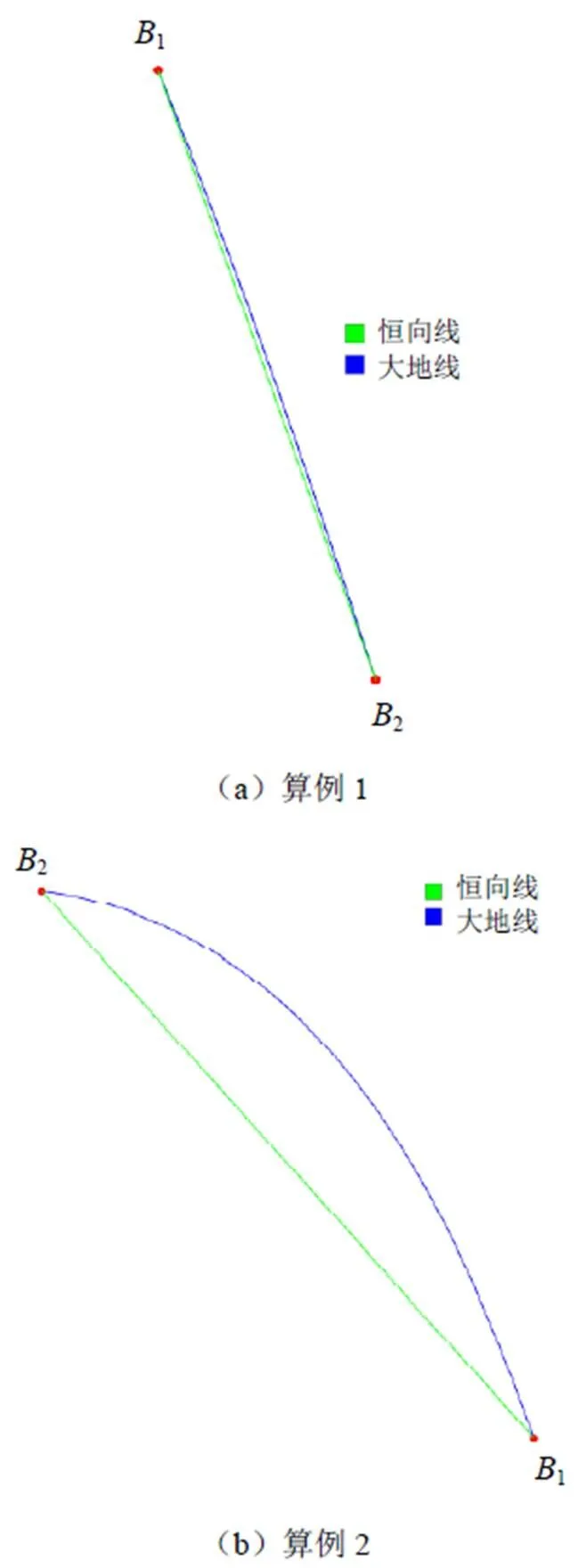
大地线是地球椭球体上的最短曲线,其在地图平面上的视觉表现会因为不同的地图投影而发生变化。常用的地图投影除了Mercator投影还有Gauss投影和Lambert投影。Gauss投影虽然较大程度地降低了地图投影产生的变形,但是并没有保持真实的方向,因此图6可以看出恒向线在该投影上表现为一条曲线,大地线则因为投影变形较小更加满足其为最短路径的视觉定义。Lambert投影是拟定的正形圆锥投影,常用的包括:Lambert Conic Conformal投影和Lambert Azimuthal EqualArea投影,前者适合中纬度东西方向的地图绘制,变形较小,因此可以看出图7中算例2的大地线绘制中,能够较好地满足大地线为最短曲线的视觉效果。总而言之,在短距离的大地线展绘中,不同投影大地线与恒向线的差别不大,而长距离的大地线展绘,不同投影性质下的地图投影会影响其展绘的视觉效果,同时地图投影参数如Central Scale Factor等的设置也会进一步影响其视觉效果,Mathematica强大的绘图能力进一步提高了大地线的应用价值。


4 结语
本文在利用Mathematica强大的数学分析功能探究大地问题正反解算法的基础上,通过将等间距内插展绘的应用扩展至展绘精度及内插间距自动调节的自适应模型,同时利用Mathematica强大的绘图能力,实现了常用投影的大地线高效展绘,得出了以下结论。
1)本文利用第三扁率对大地问题正反解的算法进行改化,提高了大地问题正反解的计算精度和计算效率,同时利用法截线方位角与大地方位角的数学关系,通过修正项的引入降低了大地方位角的计算误差。
2)针对大地线是一条空间曲面曲线的特殊性,提出了基于等间距的内插方法,通过内插点线段连接的方法提出了大地线展绘的基本思路,同时利用Mathematica设计了内插间距的自适应模型,在提高精度的情况下同时提高了展绘效率。
3)结合大地线可视化的具体应用场景,利用Mathematica强大的制图功能展示了大地线与恒向线的关系,并根据不同距离和不同应用场景对不同投影下的大地线展绘进行了初步探究,提高了其应用价值,对后续具体科学问题的探究打下了基础。其使得展绘算法的应用不再局限于墨卡托投影平面,具有一定的科学性。
[1] 边少锋,李厚朴. 大地测量计算机代数分析[M]. 北京:科学出版社,2018:9-23+38-42.
[2] 董箭,李彬彬,彭认灿,等. 顾及拱高误差的墨卡托大地线快速展绘算法[J]. 测绘科学,2020,45(9):43-51.
[3] 张晓东,涂玲,刘宝. 基于Mathematica的控制系统根轨迹探究性实验[J]. 实验技术与管理,2022,39(12):163-168.
[4] 郑天瑞. 利用Mathematica求解正轴圆锥投影的标准纬度[J]. 现代导航,2022,13(5):383-386.
[5] 吴祖新,郑中义. 大地线航法在智能船舶上的应用[J]. 舰船科学技术,2023,45(1):180-185.
[6] 纪兵,边少锋. 大地主题问题的非迭代新解[J]. 测绘学报,2007(3):269-273.
[7] CHANG S,JI B,WU M,et al. Evaluation of Height Correction on Loran Signal's Groundwave Transmission Delay Model[J]. IEEE Antennas and Wireless Propagation Letters,2022:1-5.
[8] SEIF M R,GHALENOEI E. Numerical determination of the geodesic curves: the solution of a two-point boundary value problem[J]. Earth Observation and Geomatics Engineering,2018,2(1):26-35.
[9] PEŠKA P,MIKEŠ J,RÝPAROVÁ L. Almost Geodesic Curves as Intersections of n-Dimensional Spheres[J]. Lobachevskii Journal of Mathematics,2022,43(3):687-690.
[10] BASELGA S,MARTÍNEZ-LLARIO J C. Intersection and point-to-line solutions for geodesics on the ellipsoid[J]. Studia Geophysica Et Geodaetica,2017:1-11.
[11] 计宇阳,金立新,丁佳波. 复数高斯投影的大地线曲率与代曲直距[J]. 海洋测绘,2021,41(6):31-35.
[12] 周江华,苗育红,成文生,等. 贝塞尔大地反解问题的高效率算法[J]. 测绘学报,2002(2):108-111.
[13] 唐红涛,王微,杨永崇,等. 椭球面上绘制大地线的算法[J]. 测绘科学,2015,40(4):7-10.
[14] 刘文超,卞鸿巍,王荣颖,等. 大椭圆航线设计的空间矢量方法[J]. 测绘学报,2015,44(7):741-746.
[15] 王海鹰,闫浩文,梁晓鹤. 经典范畴认知下地图的局限性[J]. 海洋测绘,2023,43(1):78-82.
[16] 赵自豪,李鹏慧. 最小径集求解方法及Mathematica实现[J]. 湖南科技大学学报(自然科学版),2022,37(2):27-32.
Efficient Mapping of Common Projected Geodetic Lines and Mathematica Implementation
ZHOU Dongquan, LIU Min, WEI Chong, BIAN Shaofeng, ZHANG Siyuan
In view of the complexity of geodetic line equation and the difficulty of efficient plotting, the formula of the forward and backward solutions of geodetic problem with third flatteningis changed, the accuracy of geodetic azimuth calculation according to the mathematical relationship between normal transversal azimuth and geodetic azimuth is improved, and an equidistant interpolation geodetic line plotting method is proposed. A precision adaptive control model was established by using Mathematica to improve the efficiency and precision of equal spacing interpolation. Using the powerful mapping function of Mathematica, the geodetic line plotting of different map projections under different distances and application scenarios is realized, and the application value of geodetic line plotting is explored. Experimental results show that the method can achieve high efficiency geodetic line drawing of arbitrary length under the condition of controlled accuracy. Geodetic line plotting of different map projections has unique significance in different application scenarios.
Third Flattening; Mathematica; Geodetic Line Plotting; Equidistant Interpolation; Adaptive Control Model
P226
A
1674-7976-(2023)-06-422-09
2023-06-20。
周东权(1999.08—),广东化州人,硕士研究生,主要研究方向为椭球大地测量计算机代数分析。
国家自然科学基金项目(42074010)

