医用口罩过滤效率相关性正态标准化与去标准化换算

杨盛宇,方珍文,陆珊珊,赵铖光

(广西壮族自治区医疗器械检测中心,广西 南宁 541000)

过滤效率是指滤材滤除细菌等微生物气溶胶以及粉尘、雾霾等非微生物颗粒物气溶胶的水平。过滤效率是医用口罩的核心技术指标,高过滤效率是保障广大人民群众呼吸健康的关键[1]。疫情期间,新型冠状病毒导致呼吸系统的发病率和病死率急剧增加,人们对于口罩的使用量暴增[2-3]。然而过滤效率检测周期长,直接导致口罩的短缺,因此缩短过滤效率的检测周期是加快应急检验的核心,也是解决应急时期口罩短缺问题的关键。

过滤效率包括颗粒过滤效率和细菌过滤效率,其中细菌过滤效率检测繁琐,周期长,成本高;而颗粒过滤效率检测简单,周期短。若颗粒过滤效率与细菌过滤效率存在相关性,将极大地缩短过滤效率的检测周期。

疫情开始前,国内外学者在过滤效率方面进行了大量的研究。基于Kuwarbara流场理论[4-5],大量研究表明最易穿透滤材的空气动力学粒径范围为0.1～0.3 μm[6-8];Lee等[9]发现最具穿透力颗粒粒径与口罩滤材纤维尺寸呈正相关;温占波等[10]研究发现熔喷布医用口罩的过滤效率受材料纤维直径的影响,纤维直径越大,过滤效率越差;周惠林等[11]发现不同材料口罩的过滤效率不同,主要体现在对颗粒物的静电吸附和物理隔离的效果不同;Samy等[12]认为颗粒物最具穿透力粒径与流速有关;Maus等[13]使用光学计数器检测滤材对不同气溶胶的过滤效率,但无法辨别生物气溶胶和非微生物气溶胶;沈伟等[14]进行了口罩阻隔性能的研究,但没有理论支撑;Zheng等[15]发现不同形状微生物过滤效率不同,金黄色葡萄球菌一般成群聚集成束,一定气流下,碰撞打碎成单个球菌,且细胞内部承受一定撞击力(约为345～414 kPa),可近似为球形固体颗粒[16]。上述研究表明,过滤效率检测使用的气溶胶颗粒都是颗粒的空气动力学粒径,并非过滤效率相关性理论基础的物理直径。

为缓解口罩短缺带来的压力,刘思敏等[17]通过相关性分析给出试验结果,当口罩的非油性颗粒过滤效率达到86%以上时,细菌过滤效率(BFE)可达98%以上;刘兴兰等[18]指出当细菌过滤效率达到95%及以上时,颗粒过滤效率(PFE)增量变小。上述研究虽然发现颗粒过滤效率与细菌过滤效率的相关性,但相关性分析只停留在试验的基础上,并没有给出理论证明。

因此,为缩短应急时期医用口罩的检测周期,本文在国内外学者研究的基础上,从理论和试验2方面对口罩过滤效率的相关性进行探究。以几何标准偏差和几何均值为切入点,依据几何标准偏差和几何均值的数学模型,利用正态分布标准化和去标准化的换算关系,将呈现偏态分布的颗粒物粒径转化为对数呈现正态分布的粒径,在已知颗粒过滤效率的前提下,直接求解细菌过滤效率。运用统计学分析软件SPSS 17.0,对全国部分医用外科口罩过滤效率的实测结果进行统计学分析,得到细菌过滤效率与颗粒过滤效率的相关性结果,将结果与理论值相比对,进一步验证细菌过滤效率与颗粒过滤效率的相关性。

1 过滤效率的检测方法及粒径分布

1.1 口罩规格及来源

试验用口罩均为口罩生产企业送样到广西壮族自治区医疗器械检测中心的样品,其中生产企业包括稳健医疗公司、德福莱公司、宝菱康公司、方宏科技公司等,涉及口罩的规格包括长方挂耳型、平面耳挂式、DW1-S,长方形、挂耳式等。

1.2 颗粒过滤效率

参照YY 0469—2011《医用外科口罩》,使氯化钠固体颗粒气溶胶(中值直径为(0.075±0.020) μm,空气动力学粒径约为0.3 μm,几何标准偏差不超过1.86 μm)以(30±2) L/min的空气流速通过预处理的口罩,使用TSI-8130过滤效率测试仪(美国提赛环科股份有限公司)测定医用口罩的PFE。

1.3 细菌过滤效率

使用ZR-1000口罩细菌过滤效率测试仪(青岛众瑞智能仪器股份有限公司)向喷雾器中输送金黄色葡萄球菌菌悬液,收集产生的细菌气溶胶(平均颗粒直径为(3.0±0.3) μm,几何标准差不超过1.5 μm)作为阳性质控值c,再收集放入样品后采样器得到的细菌气溶胶作为试验样品计数之和T,通过BFE=(c-T)/c×100%,求得BFE。

1.4 过滤效率与粒径的正态表达

过滤效率检测使用的氯化钠固体颗粒气溶胶及细菌气溶胶都是由不同粒径大小的颗粒组成,颗粒粒径分布呈现偏向一边的拖长尾状态,颗粒粒径越小,分布量越大,粒径越大,分布量越小,故长尾处于粒径大的一边,几何均值μ为颗粒物分布的中位数,颗粒粒径分布如图1所示[1]。

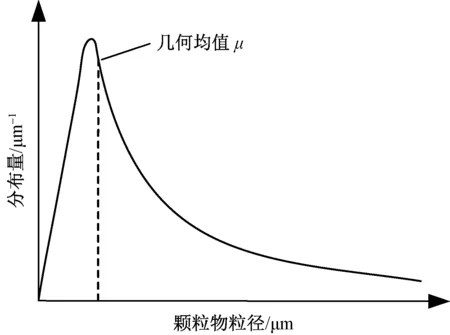
图1 颗粒粒径分布Fig.1 Particle size distribution

几何标准偏差σ是指颗粒物粒径分布偏离中值粒径(几何均值μ)的距离,几何标准偏差越大,表示偏离几何均值距离越远。颗粒物分布呈现拖长尾,但其对数后呈现正态分布。绘制氯化钠固体颗粒气溶胶和金黄色葡萄球菌气溶胶对数后的粒径正态分布图,如图2所示。

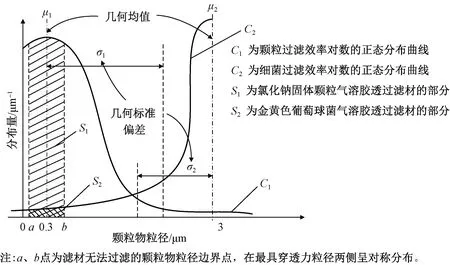
图2 颗粒物粒径对数的正态分布Fig.2 Normal distribution of particle size log

吉泽晋等[16]使用安德森采样器测定大气中的微生物,结果表明空气中没有单独的浮游菌,而是存在大小不同的菌落,滤材对菌落的过滤能力远大于对单个颗粒的过滤,即尺寸较大的颗粒物更容易被滤材过滤。在约30 L/min的空气流量下,最易穿透的颗粒粒径约为0.3 μm,穿透滤材的颗粒集中在0.3 μm的对称两侧,如图2中S1、S2所示。在已知颗粒过滤效率时,依据正态分布标准化与去标准化,可以计算出S2。当细菌过滤效率达到95%时,计算出颗粒过滤效率的最小值。

2 口罩过滤效率的相关性验证

2.1 过滤效率实测值的相关性

2.1.1 剔除离群值前过滤效率实测值的相关性

广西昌鑫、德福莱和双健等多家生产企业送样到广西壮族自治区医疗器械检测中心中的26批次医用外科口罩中的过滤效率的实测值如表1所示。对26批次口罩过滤效率的实测值进行拟合,拟合后的数学模型如图3所示。其中,拟合系数R2=0.697,表明通过实测值得到数学模型的拟合程度为69.7%,数学模型具有一定可靠性。

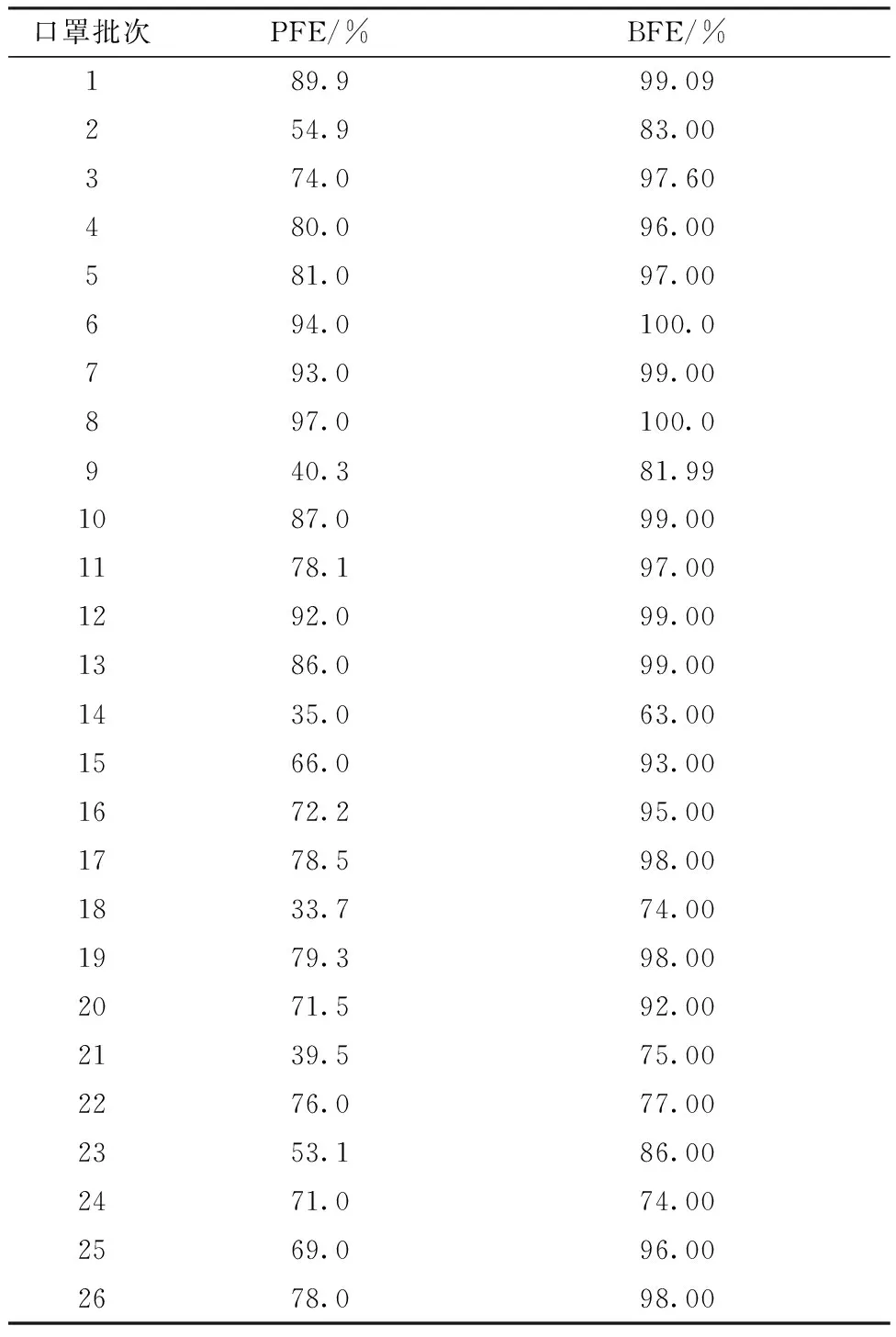
表1 过滤效率的实测值Tab.1 Measurement values of filter efficiency

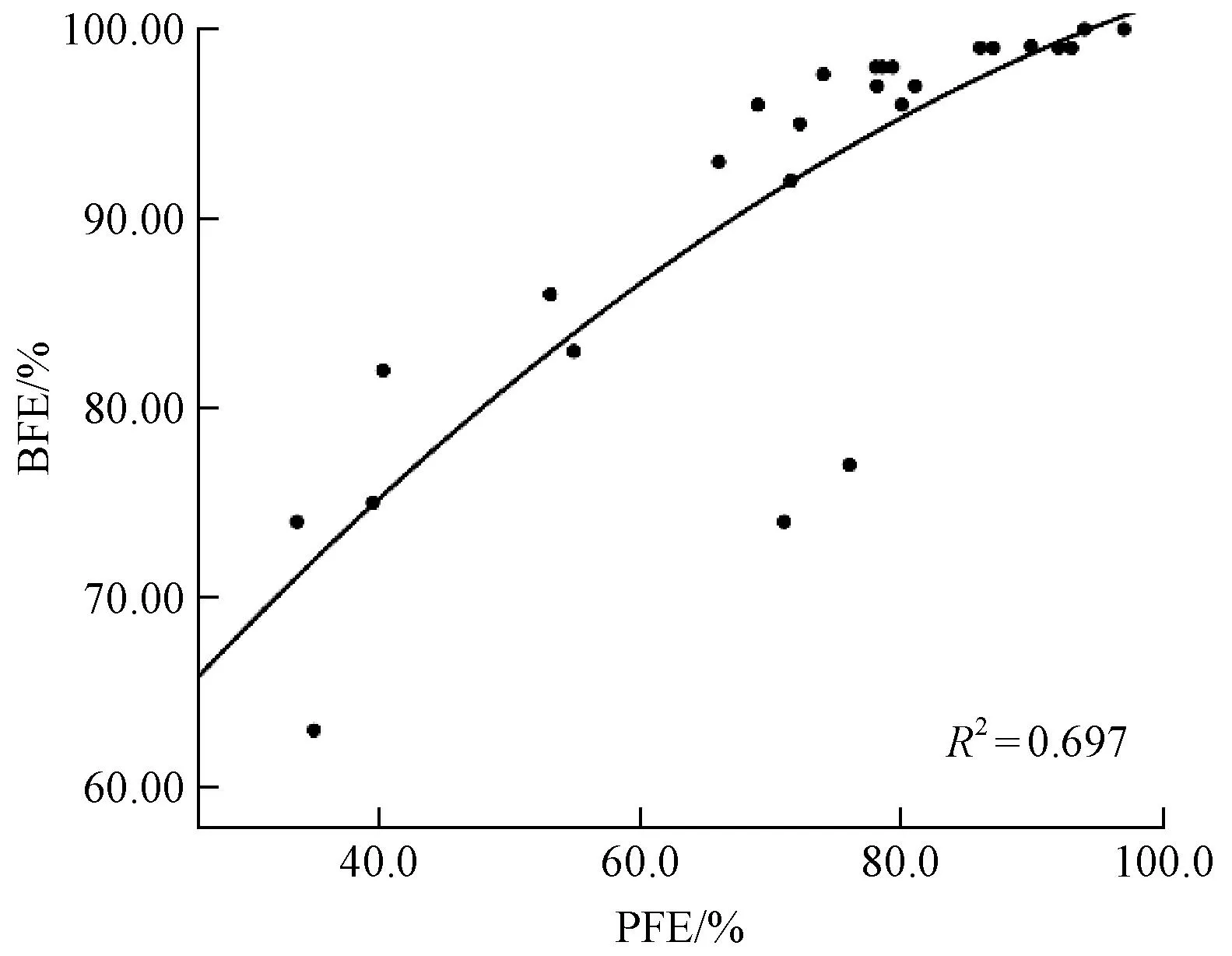
图3 过滤效率实测值的相关性Fig.3 Correlation of filter efficiency measurement values

过滤效率实测值的Pearson相关性分析结果如表2所示,相关系数为0.828,表明过滤效率在显著性水平0.01双侧显著相关。

表2 过滤效率实测值的Pearson相关性Tab.2 Pearson correlation of filter efficiency

2.1.2 剔除离群值后过滤效率实测值的相关性

为了更加直观准确地表达过滤效率间的相关性,将26批次口罩过滤效率的实测值中的3个离群值剔除后拟合的数学模型如图4所示,实测值数学模型的拟合系数R2=0.954,表明剔除离群值的数学模型可靠性更高。

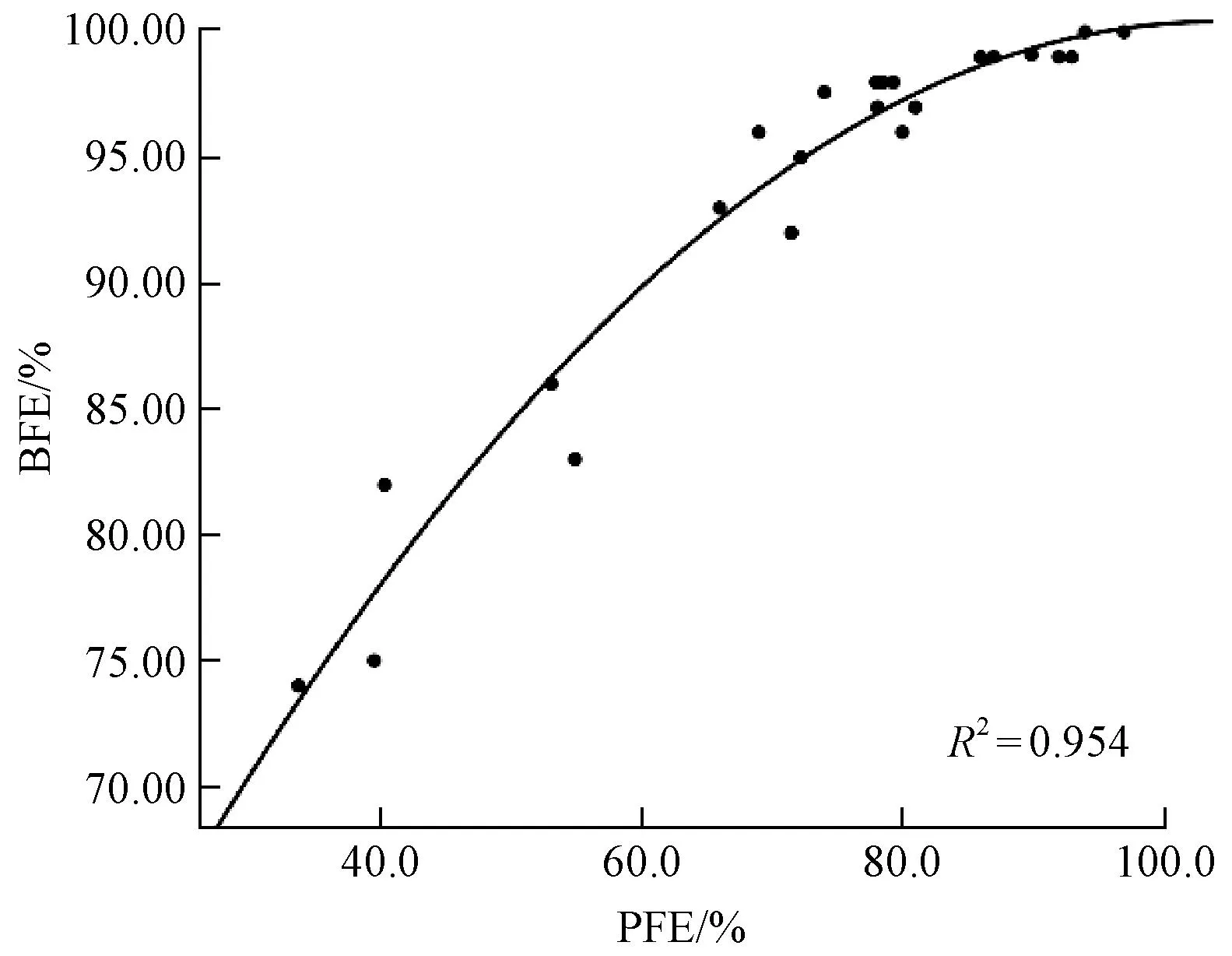
图4 剔除离群值的过滤效率实测值的相关性Fig.4 Correlation of filter efficiency measurement values after excluding outlier values

剔除离群值的过滤效率的Pearson相关性结果如表3所示,Pearson相关系数为0.950,结果表明过滤效率在显著性水平0.01双侧显著相关,相比未剔除离群值的结果,相关性更加显著。

表3 剔除离群值的过滤效率的Pearson相关性Tab.3 Pearson correlation of filter efficiency after excluding outlier values

2.2 过滤效率理论值的相关性

在已知颗粒过滤效率的前提下,可知穿透滤材的部分为S1,且该部分颗粒的粒径集中分布在0.3 μm的对称两侧。通过正态分布标准化和非标准化的换算关系,求得a、b点的坐标值(Xa,0)和(Xb,0),则函数C2在a、b点与x轴所围成的面积S2为金黄色葡萄球菌穿透滤材的部分,1-S2为细菌过滤效率。

以颗粒过滤效率PFE=87%为例,S1=1-PFE=13%,在0.3 μm对称两侧,各占6.5%。将图2中PFE的几何均值μ1标准化,转化为标准正态分布,转化后的PFE的几何均值μ=0。转化标准正态分布公式如式(1)(2)所示。

(1)

(2)

式中:Xa和Xb分别为PFE非标准正态分布标准化前a和b点的横坐标值;μ1为PFE的几何均值;σ1为PFE的几何标准差;X1和X2分别为PFE非标准正态分布标准化后a和b点横坐标值,其中X2=-X1。

标准正态分布中X2的函数值为X2对应的面积SX2,SX2=50%+6.5%=56.5%,查标准正态分布表(见表4)可知,符合SX2面积要求的数值为0.563 559,对应该面积的横列数值为0.1,纵列数值为0.06,则X2=0.16,X1=-X2=-0.16;固体颗粒气溶胶的空气动力学粒径约为0.3 μm,粒径分布呈对数正态分布,则几何均值μ1=ln 0.3,几何标准偏差σ1= 1.86,由式(1)(2)求得:

Xa=1.86×(-0.16)+ln 0.3

Xb=1.86×0.16+ln 0.3

同理,由去标准化公式(式(3)(4)),求解BFE非标准正态分布去标准化后a和b点的横坐标值X3、X4。

(1.86×(-0.16)+ln 0.3-ln 3)/1.5=

-1.73

(3)

(1.86×0.16+ln 0.3-ln 3)/1.5=

-1.34

(4)

式中:μ2为BFE的几何均值;σ2为BFE的几何标准差;X3和X4分别为BFE非标准正态分布去标准化后a和b点横坐标值。

查标准正态分布表(见表4),由a点横坐标值X3=-1.73可知,横列为1.7,纵列为0.03,对应的函数值SX3=95.82%。同理,b点对应的函数值SX4=90.99%,则S2=SX3-SX4=4.83%,即细菌过滤效率为95.17%。

同理,其他批次口罩的细菌过滤效率理论值如表5所示,当颗粒过滤效率达到87%时,细菌过滤效率可达到95.17%。

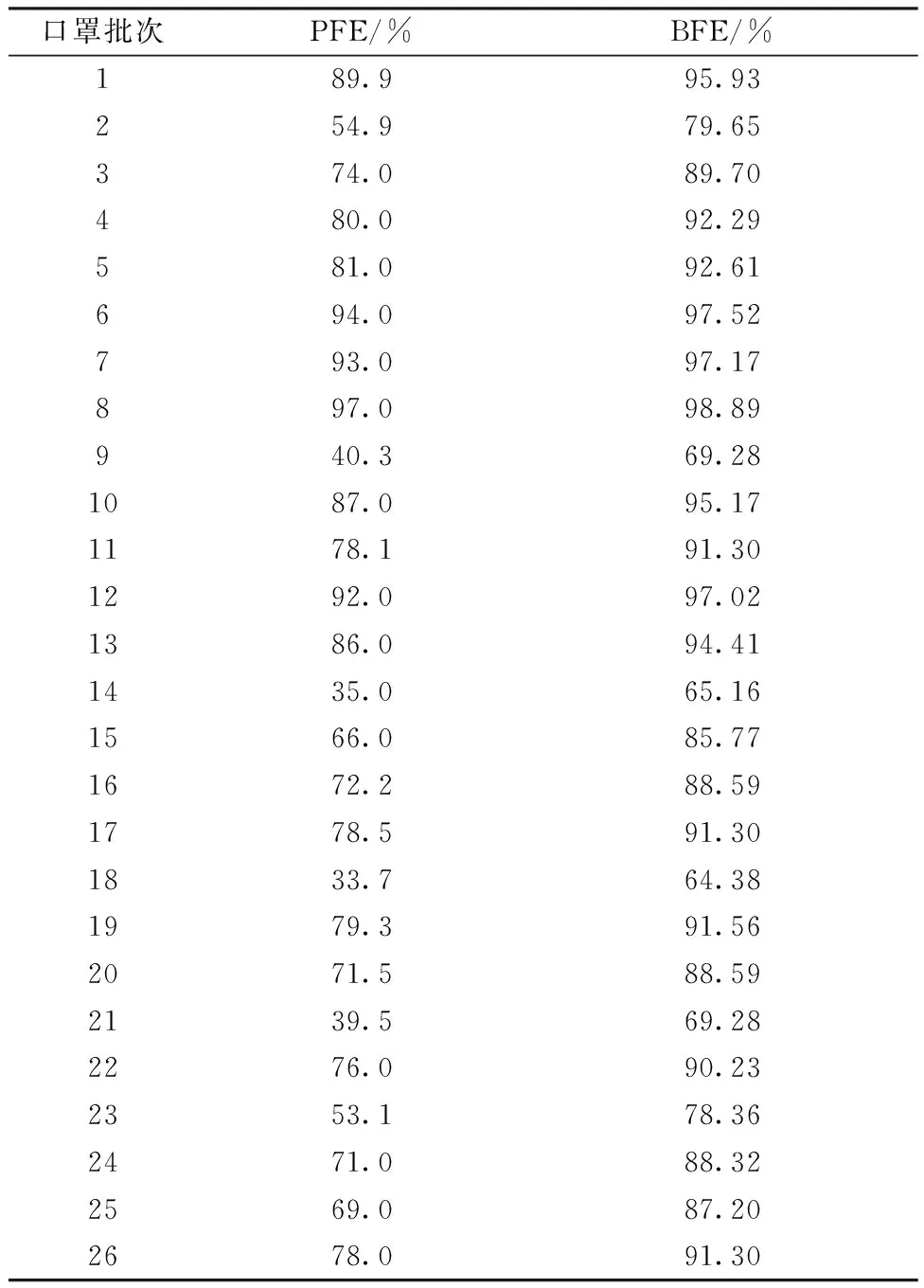
表5 过滤效率的理论值Tab.5 Theoretical values of filter efficiency

对比过滤效率实测值(表1)和理论值(表5)可知,理论值相对保守,这是由于理论值只考虑物理隔离对细菌过滤效率的影响,而实际检测中,静电吸附、滤材纤维直径等对细菌过滤效率的影响都存在差异。

对26批次口罩的细菌过滤效率的理论值进行相关性统计,结果如图5所示。过滤效率理论值的Pearson相关性如表6所示,Pearson相关系数为0.992,表明过滤效率在显著性水平0.01双侧显著相关。

表6 过滤效率理论值的Pearson相关性Tab.6 Pearson correlation of filter efficiency theoretical values

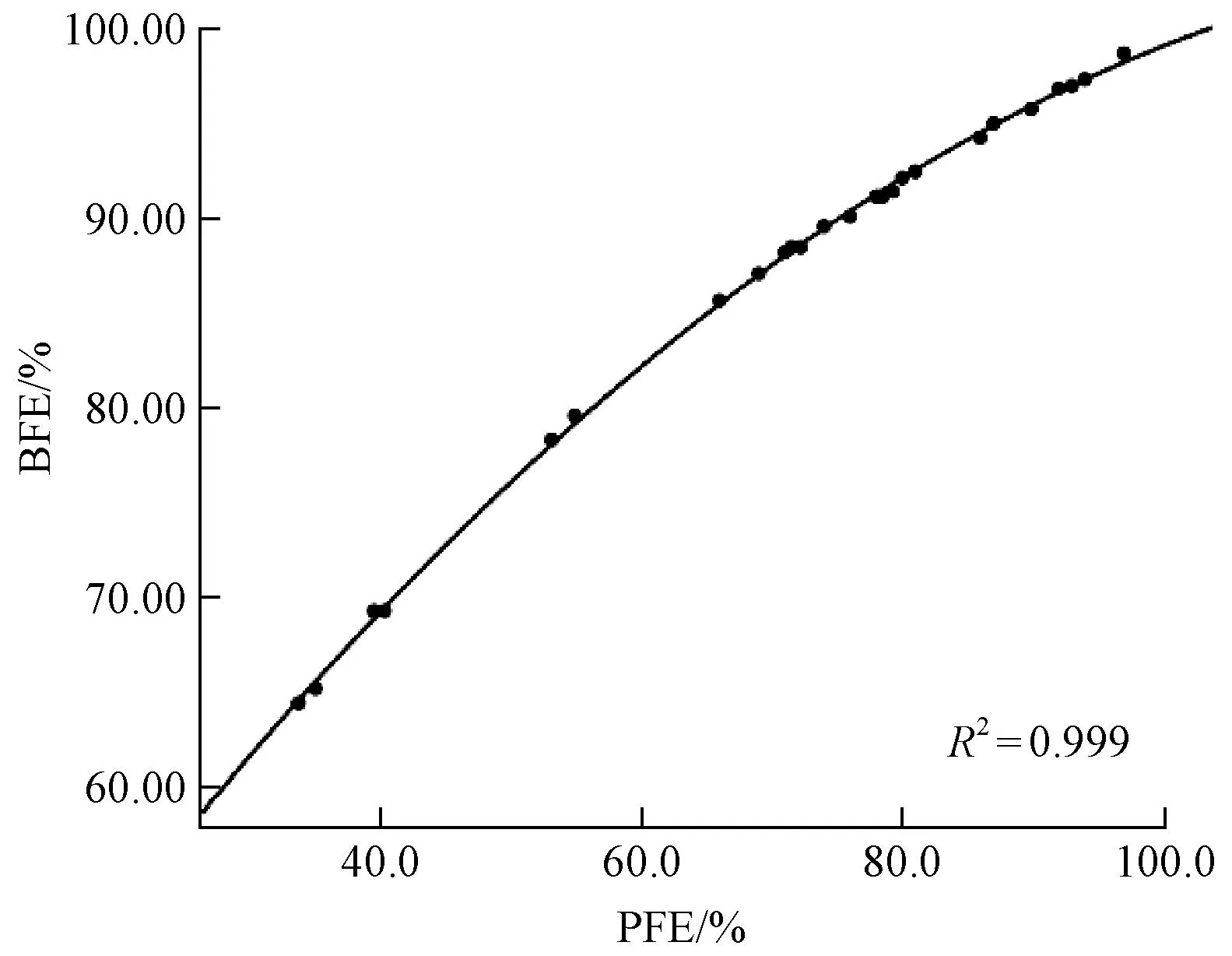
图5 过滤效率理论值的相关性Fig.5 Correlation of filter efficiency theoretical values

对比表2、表3和表6的Pearson相关性系数可知,剔除离群值前过滤效率的实测值具有一定相关性,剔除离群值后过滤效率实测值的相关性更加显著,过滤效率理论值的相关性与剔除离群值后过滤效率实测值相关性基本一致,且相关系数均大于0.9,进一步表明细菌过滤效率与颗粒过滤效率的强相关性。

3 结 论

通过正态分布标准化与去标准化的换算关系对医用口罩的颗粒过滤效率和细菌过滤效率的相关性进行理论分析和实例验证,结果表明在约30 L/min气体流量下,对实测值进行统计学分析得到的相关性系数为0.950,理论值得到的相关性系数为0.992,验证了细菌过滤效率和颗粒过滤效率在物理隔离方面有强相关性。

细菌气溶胶和固体颗粒气溶胶有着本质的区别,细菌气溶胶的传播易受外在环境的影响,环境的温度湿度等都会影响到生物气溶胶的颗粒大小、形状等,不同形状的生物气溶胶的过滤效率甚至呈倍数差异;细菌气溶胶自身的不稳定性、静电对固体颗粒气溶胶与细菌气溶胶的吸附差异均会使得细菌气溶胶过滤效率结果不稳定。因此,今后仍需针对生物气溶胶的特性,全面地分析细菌过滤效率和颗粒过滤效率的相关性。