黏土中隔舱吸力式钢圆筒安装及水平受荷试验研究
郭 伟,王吉轩,任宇晓,张 龙
(1.天津大学 建筑工程学院,天津 300072;2.天津大学 水利工程智能建设与运维全国重点实验室,天津 300350;3.天津大学 滨海土木工程结构与安全教育部重点实验室,天津 300350)
随着海洋资源开发利用及海洋贸易的不断发展,港口码头、人工岛、跨海大桥等一系列大型海洋工程建设如火如荼。由于近海区域多为淤泥质的软土地基,传统的重力式结构无法发挥其承载特性,或需对地基采用大规模的加固处理,成本较高。深埋式大直径圆筒结构因无需对软土地基进行处理的优点被广泛应用于深海人工岛[1]、防波堤[2-3]等项目建设中。但深埋式大直径圆筒结构在安装时往往需要配备振锤振动下沉,对施工环境条件、施工装备、施工控制技术等要求较高,且振动下沉过程中,会对地基土产生较大的扰动。
基于上述背景,结合深海吸力式基础[4-5]采用负压吸力安装的方式,提出新型的隔舱吸力式钢圆筒作为岛壁或码头岸壁结构,在钢圆筒内部设置隔舱板,将结构分为上下两个隔舱,通过对下舱抽气实现隔舱吸力式钢圆筒在负压吸力作用下的下沉安装,安装到位后向其上舱装入填料增加其整体稳定性。
吸力式基础在安装时受到的阻力包括筒壁与土体之间的摩阻力、筒裙端部的端阻力。吸力式基础安装理论比较完善[6-7],影响吸力式基础贯入深度的重要因素是“土塞效应”[8-9],土塞高度受基础尺寸、土壤性质以及负压大小影响[10-12],同时也有相应的土塞高度预测方法[13]为吸力式基础安装提供理论参考。
大直径钢圆筒岛壁结构以及类似的筒型基础式防波堤等结构,在安装完成后其所受的外荷载主要是水平荷载,破坏模式一般为平动或转动[14-16],结构承载力主要由地基土的法向土抗力、筒土间的切向摩阻力以及筒裙端部的端阻力提供,承载力理论计算方法主要是极限平衡法[17-20],结构的承载特性与筒土接触面积及地基土的土壤性质密切相关[21-25]。因此为保证钢圆筒承载力,应尽量保证地基土的均质性及完整性,提高筒土协同承载能力。
综上所述,目前关于大直径钢圆筒岛壁结构的研究主要集中于结构的承载特性,而对于如何优化传统大直径钢圆筒岛壁结构的安装过程尚存在空白。针对所提出的隔舱吸力式钢圆筒岛壁结构,设计完成了该隔舱吸力式钢圆筒关于安装和承载的室内模型试验,同时将传统大直径钢圆筒结构设置为对照组,对比了二者下沉阻力及水平承载特性等指标,在此基础上讨论了改变上下隔舱高度比对隔舱吸力式钢圆筒土塞发育及承载特性的影响。
1 模型试验设计
1.1 试验布置
图1和图2所示分别为贯入和承载试验布置,模型箱尺寸为1.5 m×1.0 m×1.0 m(长×宽×高),模型箱底部铺设200 mm 厚粗砂层用于固结过程排水,上覆500 mm 厚黏土,黏土层上加入20 mm 厚水层以模拟海洋环境。
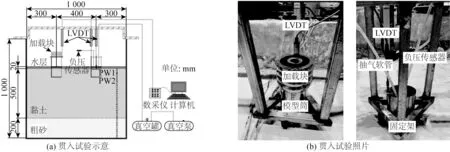
图1 贯入试验布置Fig.1 Schematic diagram of penetration test layout

图2 承载试验布置Fig.2 Schematic diagram of bearing capacity test layout
贯入安装试验中,为保证钢圆筒的垂直贯入,将钢圆筒放置于带有滑轮的固定架中,固定好LVDT,连接好负压传感器及抽气设备。钢圆筒首先在自重作用下,下舱形成密闭空间,之后打开真空泵通过逐级施加真空吸力控制钢圆筒匀速缓慢下沉至最终位置时结束负压贯入试验。作为对照组的压力贯入试验中,固定好LVDT后逐级添加加载块至钢圆筒贯入到指定位置时结束压力贯入试验。
贯入试验完成后,静置一周,进行水平承载力试验,在固定好LVDT、激光位移传感器及倾角传感器后,采取逐级加载的方式进行加载,每级荷载下钢圆筒位移稳定后施加下一级荷载,当某级荷载作用下位移开始急剧增大时,视为钢圆筒达到破坏状态,此时结束试验。
负压吸力由模型箱外的真空泵及真空罐逐级施加,通过在筒顶逐级施加加载块完成压力贯入,通过滑轮组将砝码的重力转化为施加在钢圆筒上的水平荷载。负压贯入过程中筒内负压通过负压传感器测量(型号:CYYZ11-B-62),量程-20 kPa,精度0.5%,贯入过程中土塞发育及钢圆筒的贯入深度通过固定在模型箱横梁上的位移传感器LVDT进行测量(型号:5G107),量程200 mm,精度0.25%。
承载力试验中钢圆筒水平位移通过固定在模型箱横梁上的位移传感器LVDT以及侧面的激光位移传感器进行测量(型号:AM-D100),量程100 mm,精度0.1%;钢圆筒的转角由固定在筒顶的倾角传感器测得,精度0.01°;试验数据通过数采仪(型号:DH3861N)实时记录。
1.2 模型筒
试验采用钢制钢圆筒模型,模型直径D=100 mm,长度L=200 mm,长径比L/D=2,上、下舱高度分别为L1、L2,钢圆筒筒壁厚度t1=1 mm,隔舱板厚度t2=2 mm。在隔舱板中间开口通过直线轴承连接一根不锈钢棒,不锈钢棒一端固定轻质垫片,用于测量内部土塞高度,隔舱板两侧分别设有出气口连接负压传感器和真空桶,模型筒结构如图3所示。
通过将隔舱板设置在不同高度,隔舱吸力式钢圆筒分为不同上下舱高度L1、L2,为揭示黏土地基上贯入方式及贯入深度对钢圆筒贯入阻力及承载特性的影响规律,设置了3 组不同上下隔舱高度比的隔舱吸力式钢圆筒以及1组传统钢圆筒结构模型,详细参数见表1。

表1 模型试验参数Tab.1 Parameters for model test
1.3 试验土体
高岭土是典型的海洋黏土地基,被广泛作为研究海洋工程承载特性的室内模型试验及原型试验的地基土体[26],试验采用规格为水洗1 250 目的高岭土模拟软黏土地基。采用堆载固结的方式提高试验槽中高岭土泥浆强度,固结压力15 kPa。试样具体制备方式:首先试验箱底部铺设排水管网,并在排水管上缠绕土工布,上覆厚度200 mm 的饱和粗砂作为反滤层,并在粗砂表面铺设土工布以增强排水效果;之后将高岭土粉末与水充分混合,制备成含水率46%的高岭土泥浆,将其倒入模型箱,厚度500 mm;最后在泥浆上部铺设土工布和50 mm厚的细砂层,依次放置加载板及加载块,使高岭土泥浆均匀受荷。
固结过程中,通过高岭土泥浆内距水面0.10 m、0.18 m 孔压计PW1、PW2 测量土体中超孔压消散情况如图4所示,超孔压数据采集时间为46 d。堆载初期土体内部超孔压升高,随着固结时间的增长超孔压逐渐消散,土体内部孔压趋近静水压力。

图4 超孔压消散曲线Fig.4 Dissipation curve of excess pore pressure over time
通过模型箱上布置千分表测量固结过程中土体沉降如图5所示,堆载初期土体沉降较快,随着时间的发展,土体沉降逐渐趋于稳定,固结完成后高岭土土体沉降26.04 mm。随着土体内部超孔压消散至静水压力,土体内部有效应力增大,土体固结沉降趋缓。

图5 土层沉降曲线Fig.5 Settlement curve of soil layer
固结完成后,采用十字板剪切仪测定不排水抗剪强度Su,采用烘干法测定含水率,采用环刀法测定密度,采用液塑限联合测定仪测定液塑限,得到土体主要参数见表2。

表2 高岭土物理力学参数Tab.2 Physical and mechanical parameters of kaolin clay
2 贯入试验结果与分析
2.1 所需负压及贯入阻力分析
Houlsby和Byrne[7]指出,黏土中吸力式基础贯入过程所需吸力可按式(1)计算:
式中:h为吸力式基础贯入深度;Do、Di分别为外径和内径;αo、αi分别为外、内摩阻力因子,钢圆筒外壁较光滑,分别取0.20、0.25;Nc为承载力系数,一般取9;γ'为黏土有效重度;V为吸力式基础自重。
得到采用吸力贯入的C1、C2、C3钢圆筒贯入过程所需吸力与Houlsby理论[7]计算值对比如图6所示。可以看出,在贯入初期,理论计算所需负压略大于实际负压,这是因为理论计算值并未考虑吸力式钢圆筒的初始贯入深度,试验中需要下舱在自重作用下贯入土中一定深度形成密闭空间才能继续施加负压。随着贯入深度的增加,理论计算结果与试验结果十分接近,Houlbsy和Byrne[7]关于吸力式沉箱下沉所需吸力值的计算方法同样适用于隔舱吸力式钢圆筒下沉吸力值的计算。
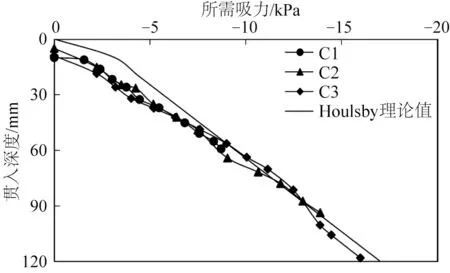
图6 所需吸力与理论值对比Fig.6 Comparison of required suction and theoretical value
贯入过程中,采用逐级加载的方式控制钢圆筒匀速缓慢下沉,因此钢圆筒的贯入阻力与施加压力相等,得到负压贯入的C1、C2、C3钢圆筒以及压力贯入的C4钢圆筒贯入深度与贯入阻力对比如图7所示。

图7 不同贯入方式贯入阻力对比Fig.7 Comparison of penetration resistance of different penetration modes
在贯入深度为0~27.8 mm时,采用负压贯入的C1、C2、C3隔舱吸力式钢圆筒贯入阻力与采用压力贯入的C4 传统大圆筒结构阻力近似相等,在贯入深度大于27.8 mm 时,负压贯入克服的阻力小于压力贯入克服的阻力。对于相同贯入深度C2、C4 钢圆筒,采用负压贯入的C2 筒达到最终贯入深度时,对应贯入阻力109.5 N,而采用压力贯入的C4 钢圆筒达到相同贯入深度时,贯入阻力为118.6 N,采用吸力贯入的贯入阻力相比压力贯入的贯入阻力减小了7.67%。这是因为施加负压吸力时,在渗流作用的影响下,减小负压下沉时筒裙端部端阻力,使得负压贯入的阻力小于压力贯入的阻力,减小值为吸力值与筒裙端部面积的乘积[7]。当施加负压较小时,负压对于端阻力的减小效果并不明显,随着负压的增大,减阻效果逐渐增大。且试验中的高岭土为黏性土,渗透系数较小,实际地基土一般是由黏土、粉土、砂土组成,其渗透系数较大,因此在实际工程中负压减阻效果更明显。
2.2 土塞特性分析
土塞发育的评价可根据m法[13],m值等于土塞体积与钢圆筒筒裙贯入深度体积的比值,如式(2)所示。可以用于预测特定尺寸吸力式筒型基础土塞高度。
式中:hp为土塞高度。
通过筒内的土塞测杆测得贯入完成后不同上下隔舱高度比L1/L2的钢圆筒内土塞高度如图8所示,L1/L2=2.28、1.00、0.56的C1、C2、C3钢圆筒的土塞高度分别为1.44、4.99、8.87 mm,土塞高度占下舱L2的高度比例分别为2.36%、4.99%、6.93%。下舱高度越大,负压贯入过程中其土塞所占比例越高。图8 中直线为m法预测土塞高度,m=0.6,m法在负压较小时预测土塞高度较为准确;随着贯入深度的增大,施加负压逐渐增大,过大的负压会导致地基土加速涌入舱内[27],使得C2、C3钢圆筒在贯入后期土塞高度增长较快,m值与试验误差较大。这是因为在确定m值时,便假定土塞高度随着贯入深度的增加成比例匀速增加,未考虑负压的增大会导致筒内土塞加速隆起。
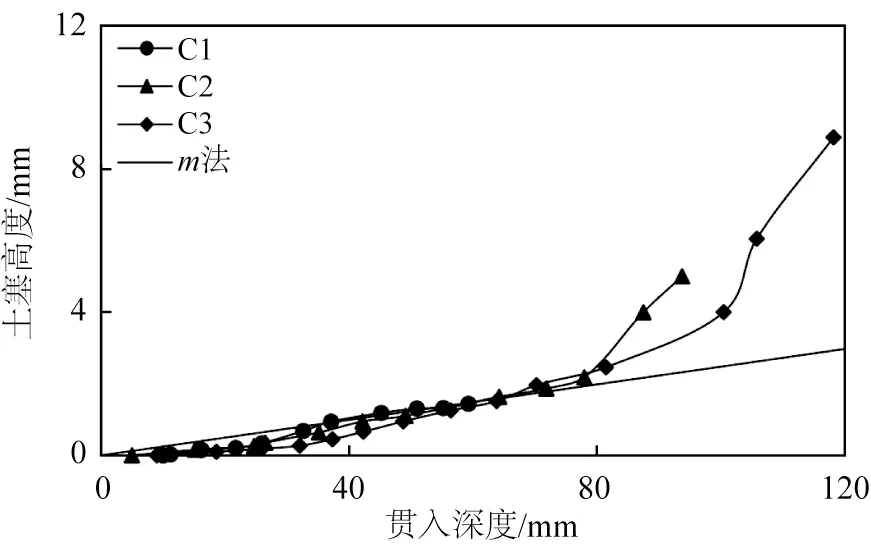
图8 不同上下隔舱高度比钢圆筒土塞高度Fig.8 Soil heave plug of bucket with different upper and lower ratio
3 水平承载力试验结果与分析
3.1 水平承载力分析
对比不同钢圆筒承载特性,根据Kelly等[28]的归一化方法,可用式(3)所示:
式中:H为水平荷载;Hm为平均水平承载力;u为水平位移;OOCR为黏土超固结比,f4表示Hm/(SuD2)和u/D关系的无量纲函数。
得到C1、C2、C3、C4 钢圆筒归一化荷载—位移曲线如图9 所示。从图9 中可以看出,当归一化水平位移位于0~0.02 之间时,相同贯入深度下,有、无隔舱板的C2、C4 钢圆筒承载力近似相等;当归一化水平位移位于0.02~0.05之间时,拥有隔舱板的C2钢圆筒承载力略大于C4钢圆筒;当归一化水平位移大于0.05时,拥有隔舱板的C2 钢圆筒与C4 钢圆筒承载力差值进一步增大。在C2 钢圆筒达到最大归一化水平位移0.178 时,归一化水平承载力为1.036;相同的位移下,C4钢圆筒归一化水平承载力为0.942,相比于无隔舱板的C4钢圆筒,拥有隔舱板的C2 钢圆筒承载力提高了9.98%。这是因为钢圆筒在受到水平荷载作用下发生转动,产生水平位移的同时,还会产生竖向位移。拥有隔舱板的C2钢圆筒下舱土体会限制钢圆筒竖向位移从而限制钢圆筒的变形,使其承载力获得提高。在受荷前期,钢圆筒变形较小,隔舱板对钢圆筒位移限制较小;随着施加荷载增大,钢圆筒位移的增大,隔舱板对钢圆筒位移限制效果逐渐明显,拥有隔舱板C2钢圆筒抵抗变形能力增强,承载力逐渐提高。在实际工程中,钢圆筒在振动下沉的过程中,地基土强度有所降低,其承载力相应也会降低。但由于试验条件所限,文中采用静压下沉,并未对地基土造成振动破坏,C4 钢圆筒承载力与C2钢圆筒承载力差幅大于试验中的差值。
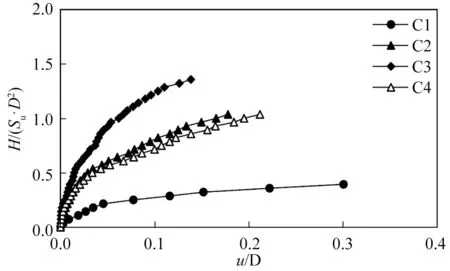
图9 不同钢圆筒归一化荷载—位移曲线Fig.9 Normalized load-displacement curve of different buckets
采用切线交点法[29]得到上下隔舱高度比L1/L2=2.28、1.00、0.56的C1、C2、C3钢圆筒归一化的极限水平承载力分别为0.290、0.680、1.036,对应的筒顶归一化水平位移分别为0.116、0.072、0.067,如图9 所示。L1/L2从2.28 降低到1.00、0.56,归一化的极限水平承载力提高了134.48%、257.24%,水平位移减少了37.93%、42.24%。说明在L/D为定值的情况下,提高钢圆筒下舱高度对提高承载力作用显著。而对于限制位移效果小于承载力。这是由于钢圆筒插入深度越大,地基土提供的土抗力越高,相应的承载力也越高,但由于土的强度远低于筒,随着施加荷载的增大,地基土变形增大,钢圆筒变形随之增大。
同时从试验中观察到,拥有隔舱板的钢圆筒C2,其破坏模式:如图10(a)所示的阶段1,钢圆筒与土体紧密贴合至远离受力侧土体与钢圆筒恰好分离出现裂缝,此时对应归一化水平荷载为0.5;如图10(b)所示的阶段2,筒土之间的缝隙逐渐发展,至钢圆筒与土体显著分离为临界破坏状态,此时对应归一化的极限水平荷载为1.036。

图10 C2钢圆筒破坏模式Fig.10 Failure mode of bucket C2
无隔舱板的传统钢圆筒C4,其破坏模式:如图11(a)所示的阶段1,钢圆筒与远离受力侧部分土体形成整体与地基土分离,且距钢圆筒0.6D处地基土出现裂缝,此时对应归一化水平荷载为0.5;如图11(b)所示的阶段2,阶段1的筒土整体出现分离且与地基土裂缝增大,达到临界破坏状态,此时对应归一化的极限水平荷载为1.036。

图11 C4钢圆筒破坏模式Fig.11 Failure mode of bucket C4
从图10 和图11 中可以看出,相同贯入深度下,有、无隔舱板的C2、C4 钢圆筒模型在水平荷载作用下其破坏模式都可分为两个阶段,但筒土破坏趋势有所区别:无隔舱板的C4在变形时,除筒土之间出现裂缝外,远离受力侧土体也会出现破坏。这是因为施加水平荷载时,钢圆筒内部土体会出现变形,隔舱板的存在会限制下舱内部土体隆起,下舱土体也会限制隔舱板的位移从而限制钢圆筒的变形,相较于传统薄壁钢圆筒结构其抵抗变形能力较强,在施加相同的归一化水平荷载时,C4 传统钢圆筒地基土破坏区域相较具有隔舱板的C2钢圆筒大,对发挥地基承载力不利。
上下隔舱高度比L1/L2=2.28、0.56 的C1 及C3 钢圆筒临界破坏状态如图12、图13 所示,C1 钢圆筒达到临界破坏状态时,除筒土接触位置外,远离受力侧地基土出现裂缝,对于发挥地基承载力不利,C3 钢圆筒在达到临界破坏状态时,远离受力侧地基土变形较小,远离受力侧土体几乎保持了完整性。因此长径比L/D为定值的情况下,上下舱隔舱高度比越小,钢圆筒变形时地基土变形较小,稳定性更高。

图12 C1钢圆筒临界破坏状态Fig.12 Critical failure state of bucket C1

图13 C3钢圆筒临界破坏状态Fig.13 Critical failure state of bucket C3
3.2 转动中心及弯矩分析
钢圆筒在水平荷载作用下达到临界破坏状态时的转动中心按式(4)及式(5)计算[19]求得。
式中:x0为转动中心到钢圆筒中轴线的水平距离,z0为转动中心到钢圆筒顶端的垂直距离,sv1、sv2为图2(b)中钢圆筒筒顶的两个位移传感器LVDT1、LVDT2测得的位移,l为LVDT1、LVDT2水平间距的1/2,sh为图2(b)中侧面激光位移传感器测得的位移。计算得到处于极限承载力时钢圆筒的转动中心位置如图14所示。

图14 水平极限承载力时转动中心位置Fig.14 Rotation center during horizontal ultimate bearing capacity
图14显示,4组试验中钢圆筒临界破坏状态时的转动中心在水平方向上位于钢圆筒中轴线附近,在深度方向上,以筒顶的荷载作用点为基点,转动中心都位于0.8L至1.1L深度范围内。对于有隔舱板的钢圆筒而言,随着上下舱高度比L1/L2的减小,转动中心逐级上移,L1/L2=2.28、1.00、0.56的C1、C2、C3钢圆筒转动中心深度z0=0.98L、0.90L、0.87L,对应的转动中心距荷载作用点(筒顶)高度分别为196.49、180.24、175.27 mm。
采用压力贯入的C4传统钢圆筒结构转动中心距筒顶深度为203.27 mm,相同贯入深度下有隔舱板的C2钢圆筒转动中心深度为180.24 mm,C2钢圆筒的转动中心深度减小了11.33%,在施加相同的水平荷载时,水平荷载产生的弯矩值更小,稳定性更高,隔舱板的存在能提高钢圆筒的抗倾覆稳定性。
采用类似3.1节的归一化方法,可按式(6)进行钢圆筒弯矩承载力的归一化[28]:
式中:M为弯矩荷载;V为竖向荷载,即钢圆筒自重;θ为钢圆筒的转角,f3表示M/(SuD3)和θ关系的无量纲函数。
得到C1、C2、C3、C4钢圆筒归一化弯矩—转角曲线如图15所示。

图15 不同钢圆筒归一化弯矩—转角曲线Fig.15 Normalized bending moment-angle curve of different buckets
从图15 中可以得到,相同贯入深度下,有、无隔舱板的C2、C4 钢圆筒转角位于0°~0.12°之间时,所受弯矩近似相等;当转角大于0.12°时,在施加相同的水平荷载时,拥有隔舱板的C2钢圆筒所受弯矩小于C4钢圆筒,在施加最大水平荷载1.036 时,C2 钢圆筒所受归一化弯矩为1.864,转角为4.760°,C4 钢圆筒所承受归一化弯矩为2.071,转角为5.152°,有隔舱板的C2钢圆筒所受弯矩相比无隔舱板的C4钢圆筒减小了10.00%,转角减小了7.61%。不仅是由于隔舱板的存在限制了钢圆筒的位移,提高钢圆筒的稳定性;而且由于C4 钢圆筒转动中心深度比C2钢圆筒转动中心深度更深,在施加相同的水平荷载时,其所受弯矩更大,更易产生倾覆现象。
采用切线交点法[29]得到上下隔舱高度比L1/L2=2.28、1.00、0.56的C1、C2、C3钢圆筒归一化极限弯矩承载力分别为0.571、1.221、1.761;钢圆筒转角分别为4.122°、2.271°、1.675°,如图15 所示。归一化的极限弯矩承载力提高了113.84%、208.41%;转角减少了44.91%、59.36%。减小钢圆筒上下隔舱高度比L1/L2,水平承载力提高的同时,钢圆筒转动中心上移,抗倾覆稳定性得到提高。
4 结 语
针对不同上下隔舱高度比L1/L2的隔舱吸力式钢圆筒及传统钢圆筒结构开展室内模型试验,获得采用负压贯入的隔舱吸力式钢圆筒及压力贯入的传统钢圆筒结构贯入阻力及承载特性。主要得到以下结论:
1)采用吸力贯入的钢圆筒,在贯入初期,其贯入阻力与采用压力贯入的钢圆筒贯入阻力近似相等,随着贯入深度的增加,由于负压减阻效应,负压贯入的阻力小于压力贯入的阻力。且Houlsby和Byrne[7]提出的吸力式沉箱贯入阻力计算理论和Guo 等[13]提出的吸力式沉箱土塞高度预测公式同样适用于隔舱吸力式钢圆筒。
2)相同贯入深度的钢圆筒,在承受水平荷载作用时,由于隔舱板对于钢圆筒变形的限制作用,在达到相同位移时,有隔舱板的钢圆筒水平承载力相比无隔舱板的传统钢圆筒有所提高。且有隔舱板的钢圆筒转动中心较浅,在施加相同水平荷载时,所受弯矩较小。
3)在长径比L/D为定值的情况下,随着隔舱吸力式钢圆筒下舱高度增大,转动中心上移,钢圆筒承载力将显著提高。相比于L1/L2=2.28的钢圆筒,L1/L2=1.00、0.56的钢圆筒转动中心位置上移,水平极限承载力及弯矩极限承载力显著提高。

