超声振动切削钛合金振动信号及表面结构分析

党迪，吕志杰，薛磊，孙中阳

（山东建筑大学机电工程学院，山东 济南 250101）

0 引言

随着加工技术的发展，钛合金等材料在航空航天等领域应用更加广泛［1-2］。由于钛合金本身的难加工特性，在加工过程中存在着诸多问题，如钛合金高强度造成刀具的磨损、出现不规则振动；伴随表面振纹和刺耳的噪声［3-4］、切削过程中温度过高［5］。因此，在钛合金加工过程中更重视降低加工过程中的不规则振动和提高已加工面的表面质量，由此提出了新的解决方案——超声振动辅助切削，其可以降低切削温度并提高工件的表面质量［6-8］。许东辉［9］通过有限元仿真研究了不同方向的超声振动对表面残余应力的影响，发现表面残余应力随着超声振动振幅和频率的增大而逐渐增大。SHUANG等［10］通过改变超声振动的频率发现在低频时超声振动对切削力和切屑的形态影响最强，材料不规则流动时形成的锯齿形切屑和高频时形成的连续切屑，是提升加工表面质量的潜在技术。PENG 等［11］通过对比超声振动切削和普通切削，发现高速超声振动切削可以使INCONEL 718 合金的表面硬度提高50%。LU等［12］首次研究了超声振动干涉对表面纹理生成的影响，并分析表征了干涉后的纹理形貌，揭示了超声铣削参数与加工质量的关系。赵芝眉［13］通过切削力与振动信号对切削颤振预测，发现切削力与振动信号的内在关系均能代表车削的不同状态。超声振动切削是在刀尖处施加一个高频率的微小位移，不同方向的超声振动切削可以瞬时改变切削中的切削速度、进给量和背吃刀量，并与切削本身产生的振动相互耦合，降低了切削过程中的振动，以达到改善切削环境的目的［14-15］。同时，振动切削通过不断地高频率分离刀具与工件，形成了断续切削的切削状态，可以极大程度地改善切削过程中的温升，减少了刀具的磨损，并在难加工结构件的加工过程中能够提升工件表面质量［16］。

综上所述，超声振动加工能够降低切削过程中的平均切削力、最大冯·米塞斯应力（常简称为Mises应力）等，但对其加工过程中的振动信号及已加工面的表面结构研究仍较少。因此，文章使用有限元软件ABAQUS建立切削模型，对切向超声振动和径向超声振动进行仿真试验，提取并分析了仿真结果中不同振幅下切削应力和切削力，得出超声振动切削的最优切削方案，以此为基础搭建试验，研究了超声振动切削对切削过程中振动信号的影响，以及对已加工表面的结构影响，以期为超声振动加工提供更详细的技术支撑。

1 钛合金车削有限元建模

1.1 材料本构模型

切削是一个复杂的过程，切削过程中工件会发生应力、应变、热软化等方面的变化，ABAQUS 中一般通过约翰逊·库克（Johnson-Cook，J-C）本构模型计算工件力与变形之间的关系，其可以直接影响仿真结果；切削热会使工件发生热软化，改变应力、应变过程，也是影响切削质量的重要参数，J-C本构模型中需要考虑到温度变化对材料强度的影响，因此应用J-C 等向强化模型为材料本构模型［17］。其方程σ由式（1）表示为

式中A＝1 089、B＝1 092、C＝0.014、w＝0.93、m＝1.1［18］；ε为塑性应变；为应变率；为参考应变率；T为材料实时温度，℃；Tm为材料熔点，℃；Tr为环境室温，℃，

1.2 材料分离失效准则

在切削过程中要定义一个分离失效准则，使单元在受刀具外力的情况下可以变形删除，并分离成切屑。J-C剪切失效准则经常运用到切削仿真中，材料的失效过程经过弹性变形阶段、应变强化阶段，当应变强化达到顶点材料开始失效，表现在有限元仿真中即为单元删除。本模型材料的失效过程基于网格的长度变化，当网格变量达到临界值时，单元删除。塑性应变方程由式（2）表示为

式中p为压应力，Pa；q为Mises应力，Pa；d1、d2、d3、d4、d5为常数，其中d1＝- 0.09、d2＝0.25、d3＝- 0.5、d4＝- 0.014、d5＝- 3.27。

1.3 建立有限元切削模型

ABAQUS是一种解决非线性问题的工具，在ABAQUS中建立二维切削模型，分为刀具和工件两部分，其中刀具的前角为5°、后角为7°，刀尖圆弧半径为0.2 mm，在实际切削过程中刀具在短时间磨损量极小，因此刀具设为三角形网格。为了加快计算速度，将刀具设为刚体。待加工件模型的尺寸为5 mm×3 mm、应变厚度设为0.5 mm。工件受切削力变形，采用四边形网格，分析类型选择温度-位移耦合、平面应变。切削部分设置小网格提高计算精度，非切削区域设置大网格减少计算时间。环境温度设置为20 ℃，无冷却液的方式，二维正交模拟几何模型图如图1所示。

图1 二维正交模拟几何模型图

刀具和工件的材料分别为DCMT11T304LF 涂层硬质合金刀具的TiAlN涂层、钛合金，刀具和工件主要性能参数见表1。

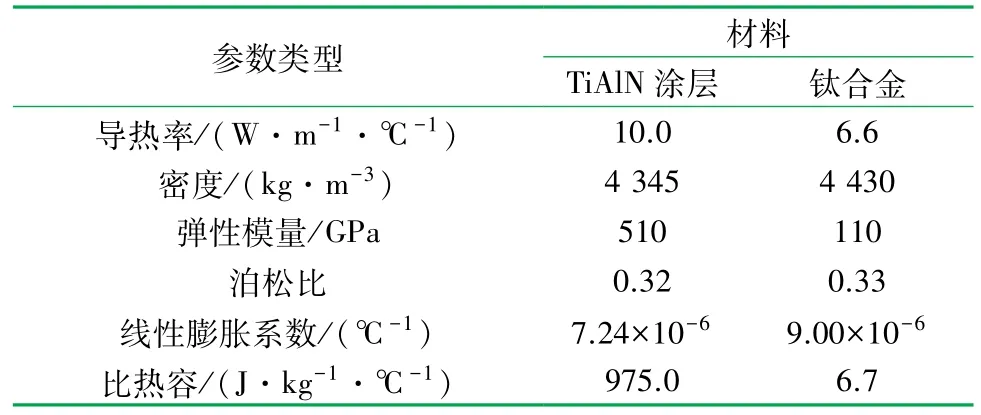
表1 TiAlN涂层刀具及钛合金材料参数表

1.4 超声振动参数设置

超声振动切削利用断续切削提高加工质量，工件与刀具接触时间称为切削有效时间，改变超声振动切削的振幅可以明显改变切削有效时间，频率对切削有效时间影响较小，因此在仿真中主要研究超声振动的振幅对工况的影响。刀具设置为刚体，参考点运动与刀具运动相同，在刀具参考点RP-1上设置超声振动位移，在设置超声振动时，选择位移边界条件，幅值选择以周期变化，在ABAQUS 中设置周期变化时，其内置的周期变化表达式a由式（3）表示为

式中傅里叶级数中的常数项A0为初始幅度；An为余弦项系数、Bn为正弦项系数，n＝1，2，3，…，N；ω为角频率，rad／s；t为时间，t0为开始时间，s。超声振动的幅值曲线可以看作一个仅包含sin 函数的简单正弦曲线，因此ABAQUS中的周期傅里叶函数可以简化，由式（4）表示为

式中ω＝125 600 rad／s；B1为所需的超声振动振幅，其值分别为0、5、10、15、20 μm。将所需的参数输入到ABAQUS 幅值周期选项中可得到刀具在切削过程中频率为20 kHz的超声振动。

将上述工件和刀具的材料参数导入ABAQUS切削仿真模型中。设置仿真试验，切削速度为60 m／min，超声振动方向选择径向和切向，振动的频率为20 kHz，考虑到超声振动切削是在刀尖添加一个微小位移，振幅过小对试验结果影响不明显，振幅过大会影响已加工表面结构，所以振幅选择为0、5、10、15、20 μm，工件的切削深度为0.5 mm，应变厚度为0.5 mm。仿真试验参数见表2。

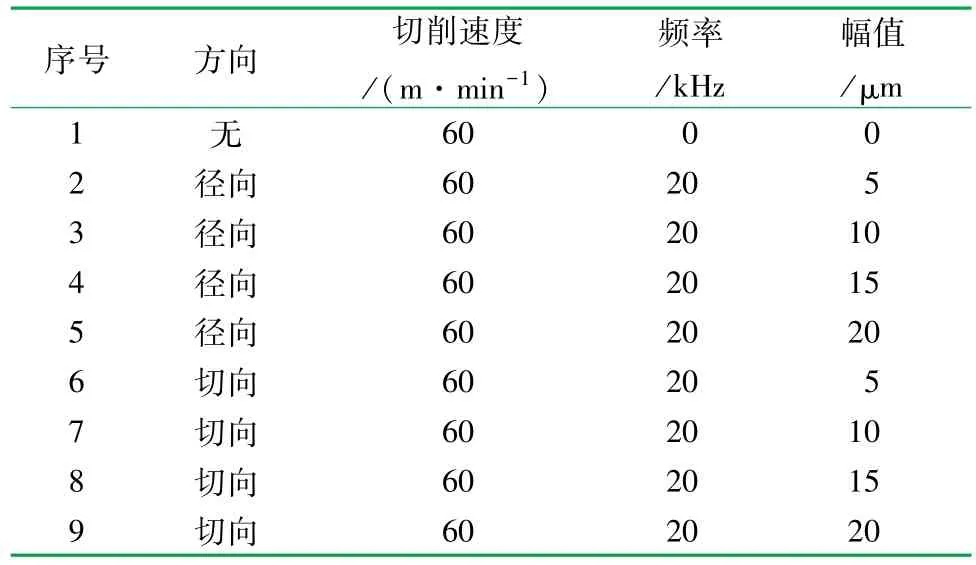
表2 超声振动模拟试验参数表

2 仿真结果及其分析

2.1 切削应力分析

Mises应力是基于剪切应变的一种等效应力，定义为当单元变形达到一定程度时材料开始屈服，一般用来衡量疲劳、破坏，最大Mises应力是切削仿真中的重要指标。将表2 中9 组试验参数导入到ABAQUS中，切削速度与切削深度不变，只改变超声振动辅助切削的振幅与方向设计仿真试验。最大Mises应力仿真结果如图2所示，不同切削条件最大Mises应力图如图3所示。

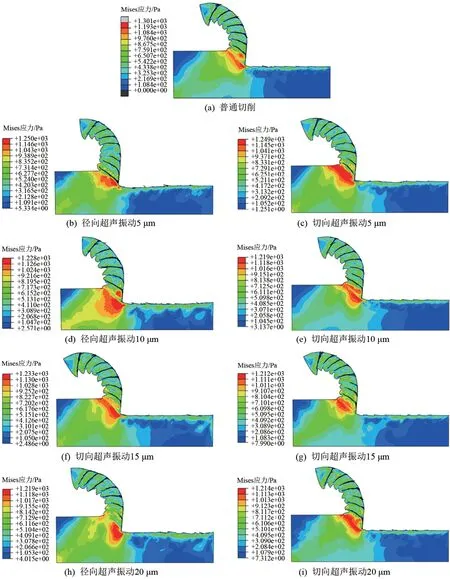
图2 普通车削与超声振动车削Mises应力云图

图3 不同切削条件最大Mises应力图

超声振动切削因其断续切削的特性可以降低过程中的加工应力，从图2、3可以看出，不施加任何方向的超声振动时最大Mises应力为1 301 Pa，由变化曲线可知在0 ～10 μm 范围内振幅对最大Mises 应力影响最为明显，其最大Mises 应力减小，振幅为10 μm时径向超声振动的最大Mises 应力为1 228 Pa、切向应力为1 219 Pa。在10～20 μm内应力趋于平稳并发生波动，说明在0～10 μm内振幅增大，最大加工Mises应力减小，并在10 μm时达到平稳，相比于普通切削约降低了6%，在10 ～20 μm 内振幅继续增大，最大加工Mises 应力不会持续大幅减小，说明在一定范围内Mises 应力会随着超声振动切削振幅增大而减小，超过了此范围，Mises 应力趋于平稳。从图3曲线可以看出径向和切向超声振动对最大Mises 应力的影响基本相同，其中切向效果略好于径向。

2.2 切削力分析

切削力的整体变化趋势与最大Mises应力减小应力的变化趋势相似，在超声振动振幅较小时切削力降低明显，随着超声振动振幅继续增大，切削力在测量范围内逐渐趋于平稳，其变化趋势如图4所示。

图4 不同振幅的平均切削力变化图

由图4 可知，当切削状态为普通切削时平均切削力最大为408.45 N，切向超声振动切削在振幅为0～10 μm时平均切削力不断减小并在振幅为10 μm时达到最小，随着振幅继续增大平均切削力增大，在超声振动振幅较小时，断续切削的作用可以减小平均切削力，当随着振幅继续变大，切向超声振动的方向与刀具的进给方向相同；随着振幅继续增大，材料容易在刀尖处形成聚集，使平均切削力变大。径向超声振动在振幅为0～10 μm时，平均切削力变化与切向超声振动相似，平均切削力在10 μm 时为365.86 N。随着振幅继续增大平均切削力继续减小，径向超声振动方向垂直与切削方向和进给方向，而随着断续切削的作用，超声振动的振幅增大，平均切削力减小；当振幅在10～20 μm后，平均切削力趋于平稳，但径向超声振动方向会改变切削的背吃刀量，超声振动的振幅过大将导致加工平面的精度降低，因此径向超声振动的振幅也不宜过大。根据径向、切向超声振动的变化可知，无论是在切向还是径向，振幅为10 μm时超声振动在降低平均切削力方面都有明显的优势，虽然继续增大振幅切向的最大Mises 应力与径向的平均切削力有继续降低的趋势，但继续增大振幅可能会对加工表面结构产生影响。

由工件切削应力分析可知，超声振动振幅在0～10 μm 时，超声振动对最大Mises 应力的影响最敏感，继续增大超声振动的振幅对最大应力并无明显影响，在分析平均切削力时振幅为10 μm 时相较于其他振幅也有明显的优势。因此选择10 μm 作为超声振动的振幅，对切削过程中平均切削力进一步分析，切削力对比图如图5所示。

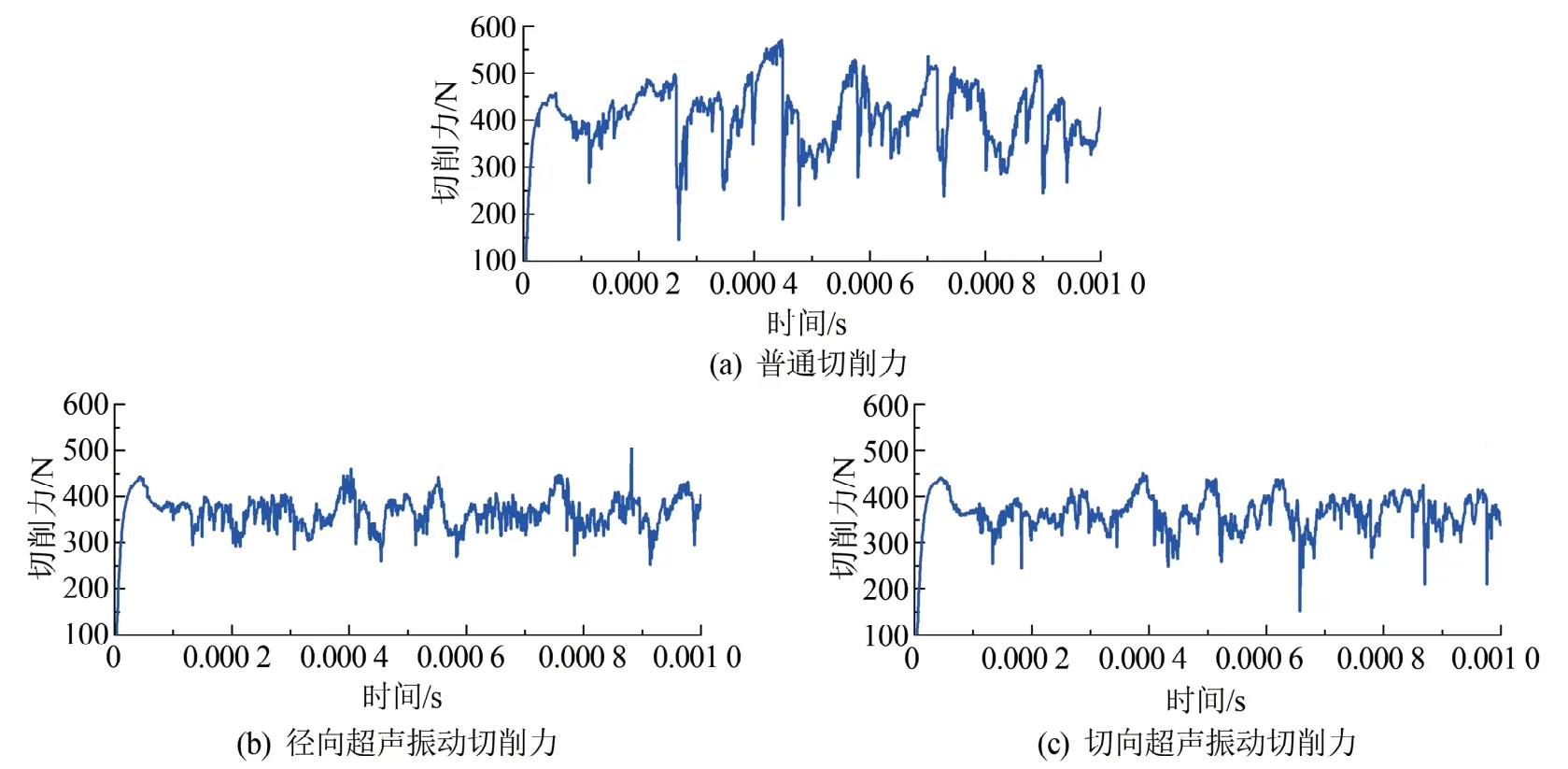
图5 各切削力对比图

钛合金切削时会形成锯齿形切屑，因此切削波动较大，由图5 可知，普通切削时平均切削力为408.45 N，并且由于锯齿形切屑的原因切削力波动非常大。径向超声振动切削的平均切削力为363.70 N，当在切削过程中施加超声振动后，虽然切屑仍为锯齿形切屑，但切削力的波动明显变小，相较于普通切削更加平稳。切向超声振动辅助切削的平均切削力为365.86 N与径向超声振动基本持平，振幅为10 μm超声振动切削可以有效降低切削过程中11.0%的主切削力。超声振动切削在切削过程中刀具与工件不断分离接触，从而形成断续切削，断续过程中刀具与工件分开时切削力大幅降低，因此超声振动切削降低了平均切削力。由径向和切向切削力分析计算可以得出径向超声振动切削切削力标准差为41.91，而切向超声振动切削力标准差为45.55，径向超声振动比切向更加平稳，切削力平稳有助于提高已加工表面的表面质量。因此试验时选择10 μm径向超声振动辅助切削。

3 试验设计及结果分析

3.1 试验设计

经过仿真分析不同切削状态下的最大Mises应力、切削力以及在振幅为10 μm 时切削过程中切削力的变化曲线，通过系统的分析对比，最终选择最优的切削方案为振幅为10 μm 时的径向超声振动辅助切削。为了探究超声振动辅助切削在实际应用中与普通切削的优缺点，必须通过实际试验验证。切削力和最大Mises应力主要受切削过程中的工件变形、切削热和加工过程中的振动耦合作用，其中最大Mises应力过大会导致切削过程不平稳，增大加工过程中系统的振动，加工过程中系统的振动会直接影响切削力是否平稳，切削力的周期性变化会使已加工表面的表面结构变差。测量切削力时，通过电阻应变式传感器测量刀杆上由切削力产生的变形，通过电路转换、放大、标定之后推算出被测的切削力。切削振动信号通过测量刀尖振动产生的位移而获得，并且信号分析可以侧面反映出切削力的大小和变化［19］。

设计一个实现超声振动辅助切削的试验，并采集振幅为10 μm 时的径向超声振动切削状态下的振动信号，与普通切削条件下的振动信号，并使用粗糙度测量仪，测量加工后的表面结构，对切削过程、试验结果两方面测量，观测超声振动辅助切削在实际工程应用中的表现，试验平台如图6所示。

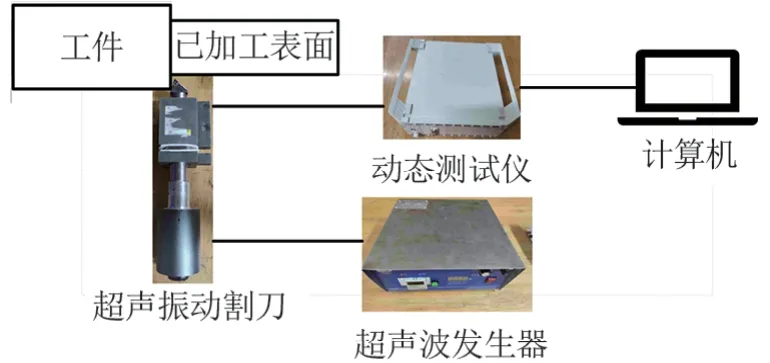
图6 试验平台图

试验平台主要由超声振动辅助加工系统、数控车削中心和动态测试系统3部分组成。超声振动辅助加工系统使用聚能超声波割刀，型号为SCQ-1500F，车床使用CY-K360n 数控车削中心，动态测试系统选用DH5923N动态信号测试分析系统，信号放大装置使用电桥应变片的方式。

由于信号频率较高，传感器选用加速度力传感器，加工件选用规格为Φ100 mm×400 mm的钛合金棒料，刀具使用DCMT11T304LF 涂层硬质合金刀具，刀具表面的涂层为TiAlN。切削试验参数见表3。

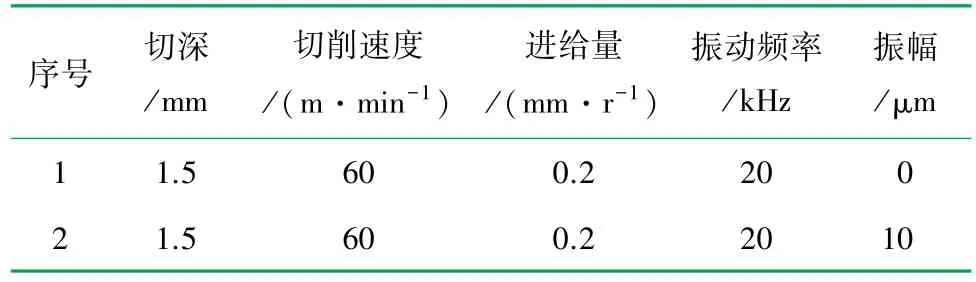
表3 切削试验参数表

3.2 振动信号结果与分析

由于在刀具与工件接触面积不变的情况下最大Mises应力过大会导致切削过程不平稳，增大加工过程中系统的振动，因此使用切削动态信号来验证仿真中的切削应力。

使用东华测试DH5923N 采集普通切削和超声振动辅助切削过程中的振动信号，利用系统中自带的算法对信号放大分析，采样频率设置为5 kHz，测量切削过程中＜1 kHz的振动信号，采样时间为10 s，可得不同切削状态下的时域信号和频域信号如图7所示。

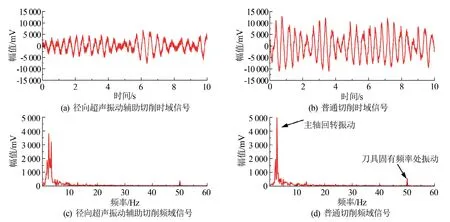
图7 切削时频域信号图

由图7（a）和（b）可以看出在相同切削条件下，普通切削采集到的时域信号从波形看信号跳动的范围比较大，证明切削过程中有比较大的振动产生。采用径向超声振动辅助切削时采集到的时域信号跳动的范围约减小了28%，说明径向超声振动辅助切削可以降低切削过程中的径向振动。由图7（d）可以看出信号的振动频率主要来源于主轴转动时产生的振动和刀具固有频率上产生的振动，由图7（c）与（d）对比峰值可以看出超声振动切削可以有效地降低切削过程中由主轴回转产生的振动和在固有频率上的振动，降幅约为22%。因此，超声振动辅助切削可以抵消机床坐标系中x轴方向的振动，提高了加工质量。

3.3 表面结构结果与分析

切削力的周期性变化会影响已加工表面的表面结构，表面结构在一定程度上体现了切削过程中切削力是否平稳，因此使用表面结构验证超声振动切削对切削力的影响。根据表3 的两组试验，分别测量普通切削与超声振动切削加工后的表面结构。选择仪器TR200粗糙度测试仪，为了保证测量准确无误，每个加工圆周面在不同地方测量3 组数据取其中间数据，可得原始表面轮廓曲线的测量数据如图8所示。

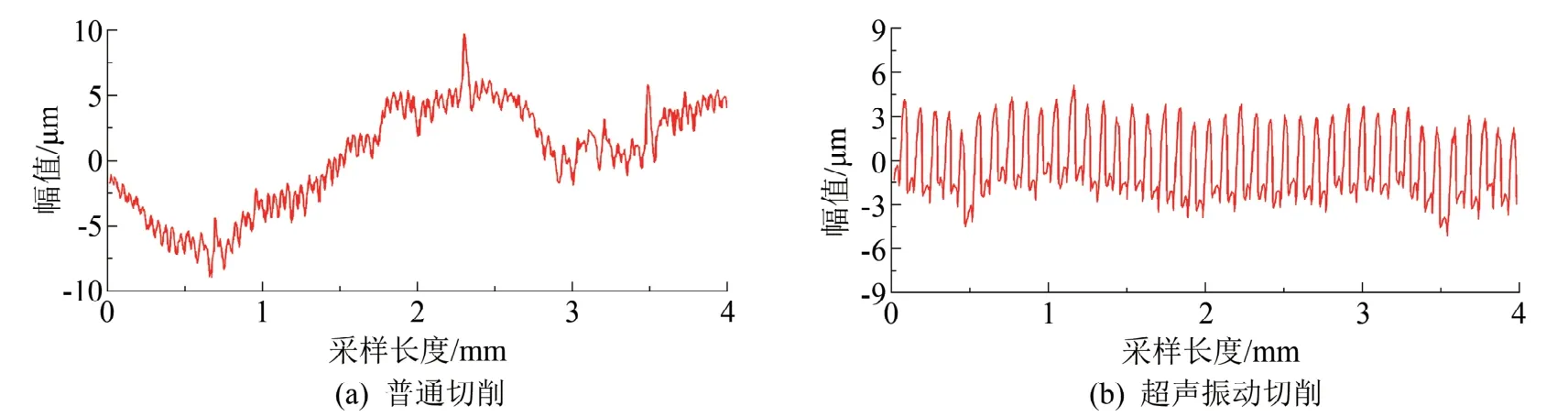
图8 不同切削状态下已加工原始表面轮廓曲线图

从加工表面原始轮廓图可以看出，普通切削状态下加工表面的表面波纹度轮廓有较大的起伏，因此采用表面结构比使用表面粗糙度和表面质量表达更合适。超声振动切削状态下加工表面的原始轮廓图的表面波纹度较小，表面粗糙度轮廓呈锯齿形曲线波动，这个波动是由于施加在刀具上的超声振动与机床在切削过程中产生的随机振动相耦合产生的，与超声振动的最大振幅相似，其频率相差较大，综合可得已加工表面原始轮廓的极差约降低了23%。结合对振动信号结果分析可知，刀具的超声振动抑制了主轴转动产生的振动和刀杆固有频率处产生的振动，但振幅过大时施加在超声振动上的规则振动会在加工表面上增大表面粗糙度轮廓，因此当超声振动方向为径向时，超声振动的振幅不宜过大，其值过大可能会使表面结构相较于普通切削变差。

4 结论

通过以上研究得出以下结论：

（1）超声振动振幅在10 μm 时，最大Mises 应力相比于普通切削降低了6%。振幅继续增大，最大加工Mises应力不会持续大幅减小，说明仅在一定范围内Mises应力会随着超声振动切削振幅增大而减小。

（2）当振幅为10 μm 时，普通切削与径向和切向平均切削力相比，超声振动切削可以有效降低切削过程中11%的主切削力，且径向切削的切削力方差小，切削过程更加平稳。

（3）超声振动辅助切削可以有效减小切削过程中振动信号的波动范围约为28%。对比频域信号可知，超声振动辅助切削能够减小主轴回转及刀架固有频率引起的振动约为22%。超声振动加工是通过耦合降低主轴回转与刀杆固有频率产生的振动。

（4）超声振动加工降低了已加工表面原始轮廓的极差约为23%，但振幅过大会影响表面粗糙度轮廓，因此当超声振动方向为径向时，超声振动的振幅不宜过大，其振幅过大可能会使表面结构相较于普通切削变差。