水合盐热化学反应器参数优化与供暖应用案例分析

葛继翔，纪明希，丁玉龙，罗伊默，王利明

（1湖南大学土木工程学院，湖南 长沙 410082；2英国伯明翰大学储能中心，英国 伯明翰 B15 2TT）

2021 年我国建筑运行能耗约占全国总能耗的21%，建筑运行产生的二氧化碳排放量占全国总排放量的19%[1]。可再生能源在建筑中的高效利用可有效减少二氧化碳的排放，其中太阳能被认为是最具潜力的可再生能源之一。然而，太阳能具有较大的波动性和间歇性，在建筑热利用过程中会造成供需不匹配的问题[2]，而储热技术可有效解决这一问题。储热技术根据原理可分为显热、潜热和热化学储热。热化学储热具有储热密度高、长期储存几乎无热损等优点，具有巨大的应用前景[3]。水合盐作为常见的热化学储热材料，具有热源温度要求低、廉价易得、环保和安全性高的特点，适用于中低温储热，其在建筑上的应用逐渐得到广泛关注[4]。水合盐储热的基本原理为：通入高温干空气，含水量高的水合盐脱水吸热；通入低温湿空气，含水量低的水合盐吸水放热，反应式可表示为：

对于水合盐储热系统而言，反应器的性能十分关键。水合盐反应器分为开式和闭式两种。总的来说，用于建筑供暖时，开式反应器比闭式更有优势，体现在易施工、体积更小、能量密度更高、初始成本低、传热效率、㶲效率和能量效率更高[5]，因此本工作针对开式反应器开展研究。目前，不少学者采用数值模拟的方法对开式反应器的性能进行了分析。Rui等[6]设计了一种新型结构反应器，通过COMSOL软件，分析了其内部反应更加均匀的原因。Humbert等[7]通过拓扑算法设计新型流道几何形状，采用COMSOL软件建立模型，分析了该结构应用于筛式反应器和圆柱反应器的性能。Li等[8]运用COMSOL软件模拟了采用溴化锶的反应器在不同工况下的充放热性能。可见，现有反应器的模拟通常采用多物理场仿真软件，在反应器的结构设计上具有一定优势，但因对计算资源要求高，无法用于反应器动态工况下的性能研究。因此，需建立适用于长时间尺度模拟的水合盐反应器动态仿真模型。

由于建筑用能的随机性以及太阳能的间歇性和波动性，水合盐热化学反应器应用于建筑储热供暖时一直在动态变工况条件下运行。因此，为提高反应器放热功率与建筑热负荷匹配度，需对其运行过程进行动态控制。Mukherjee 等[9]研究发现反应器在实际应用过程中性能会受室外空气温度和湿度影响，可通过改变湿度控制出口温度，而填充率和长径比对动态输入工况下反应器的性能有一定影响[10]。Mahon等[11]开发了一种热化学反应器与集热器耦合的储热系统并评估了其在住宅中运行的可行性，但未探讨其在供暖工况下的性能。Zondag 等[12]建立了反应器与恒温槽耦合的储热系统，仅研究了其在稳态工况下的储热与供暖性能。由于开式反应器一直在动态变工况条件下运行，工作过程是反应、热质耦合的非稳态过程。要保证反应器长期稳定运行，需对其运行过程进行动态控制。然而通过调研发现，目前有关反应器的动态性能研究还较少，缺少动态工况下反应器放热功率的控制方法研究。

因此，本工作建立了适用于长时间尺度模拟的水合盐反应器动态仿真模型；基于以上模型，对入口空气温度、水蒸气分压力、流速和反应器尺寸等因素对出口参数的影响进行了敏感性分析；以长沙某三层建筑为例，探索了提高反应器放热功率与建筑热负荷匹配度的控制策略。本工作可为水合盐热化学储热技术在实际工程中的应用提供指导。

1 数值模型

1.1 物理模型

反应器的物理模型如图1所示。为了简化反应器的模型，对控制方程做了以下假设：

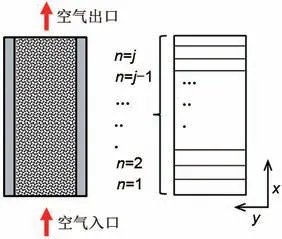
图1 反应器物理模型Fig.1 Reactor physical model

（1）假定多孔盐层中固体和气体之间存在局部热平衡，并且忽略辐射传热；

（2）湿空气由干空气和水蒸气组成，可视为理想气体；

（3）反应床的性质(比热容和导热率等)只是反应进程α的函数，不受温度的影响；

（4）反应器壁面绝热，可以忽略径向方面的传热；

（5）反应器中空气的流动是均匀的，空气流动遵循达西定律。

反应器壁面绝热，可将反应器简化为一维模型。由于溴化锶盐具有储热密度高，热源温度低，不易吸水液化，不易熔化(熔点温度88 ℃)的优点，因此选用溴化锶作为反应器中的储热材料，物性参数参考文献[6]。

1.2 控制方程

1.2.1 反应动力学方程

水合盐的吸附/脱附反应速率可以被描述为：

式中，α为反应进程，即SrBr2·6H2O的物质的量浓度与总反应盐的物质的量浓度之比；Af为考虑动力学的阿仑尼乌斯指前因子，通过特定的反应实验测量；Ea为阿仑尼乌斯活化能，kJ/mol；指数p和q在水合时取p=1，q=0，脱水时取p=0，q=1；Pv和Peq分别为水蒸气分压力和平衡压力，Pa。

在热力学平衡下，可以使用Clausius-Clapeyron方程来计算水蒸气的平衡压力：

式中，Pref为参考压力，Pa；ΔH为反应焓，kJ/mol；∆S为 反 应 熵，kJ/(mol·K)；Teq为 平 衡 温度；R为通用气体常数，J/(mol·K)。

1.2.2 守恒方程

在对以SrBr2为储热材料的热化学反应器进行模拟时需要用到质量守恒方程、动量守恒方程和能量守恒方程。本工作采用商用数学软件MATLAB对热化学反应器中的热质传递过程进行代码编写。如图1 所示将反应器划分成n个网格。采用有限容积法对传热传质过程进行数值计算，采用隐式和乘方格式对控制方程进行有限差分从而获得差分方程。使用转化式ρv=Mv×nv将质量方程中质量浓度统一转换为物质的量浓度。

湿空气的质量守恒方程为：

式中，εb为反应盐的孔隙率；nm为湿空气的物质的量浓度，mol/m3；Ψ为化学计量数，Ψ=5。

水蒸气的质量守恒方程为：

式中，ξw为湿空气中水蒸气的摩尔分数；Dwa为多孔盐层中水蒸气的扩散系数，m2/s；u为速度矢量，m/s。

空气的流动遵循达西定律，其动量守恒方程为：

式中，Pt为反应器中的局部压力，Pa；μa为空气的动力黏度，pa·s；κb为多孔盐层的渗透率，m2。

反应器中湿空气与反应盐的能量守恒方程为：

式中，nb为反应盐物质的量浓度，mol/m3；cb和cm分别表示反应盐摩尔比热容和湿空气摩尔比热容，J/(mol·K)；λeff为反应床的有效热导率，W/(m·K)。

λeff表示反应器内固体与气体的综合换热参数，可以用式(8)计算：

式中，λd和λh分别为脱水盐和水合盐的热导率，W/(m·K)。

1.3 初始和边界条件

本工作对反应器的放热/水合过程进行分析。在反应开始时，反应器中的盐被设置为完全脱水状态，对于水合过程：

反应器内部的初始温度和压力假定为与环境温度相等，水蒸气分压力等于初始温度下的水蒸气平衡压力：

气体匀速通过反应器，流速为：

式中，qm为流量，m3/h；Ab为反应器截面积，m2。

在水合阶段，环境空气直接通入反应器中，空气入口温度为：

在反应器出口设置边界条件：

式中，L为反应器长度，m。

1.4 模型验证与网格独立性验证

对反应器模型的水合过程进行了验证，将空气出口温度和湿度与Mukherjee 等[10]的模型进行比较，对比结果如图2所示。水合过程中温度的平均相对误差MRE和平均绝对误差MAE分别为4.36%和1.49 ℃，相对湿度的MRE 和MAE 分别为12.52%和1.06%。因此，本工作建立的模型和Mukherjee等[10]的模型具有良好的一致性。

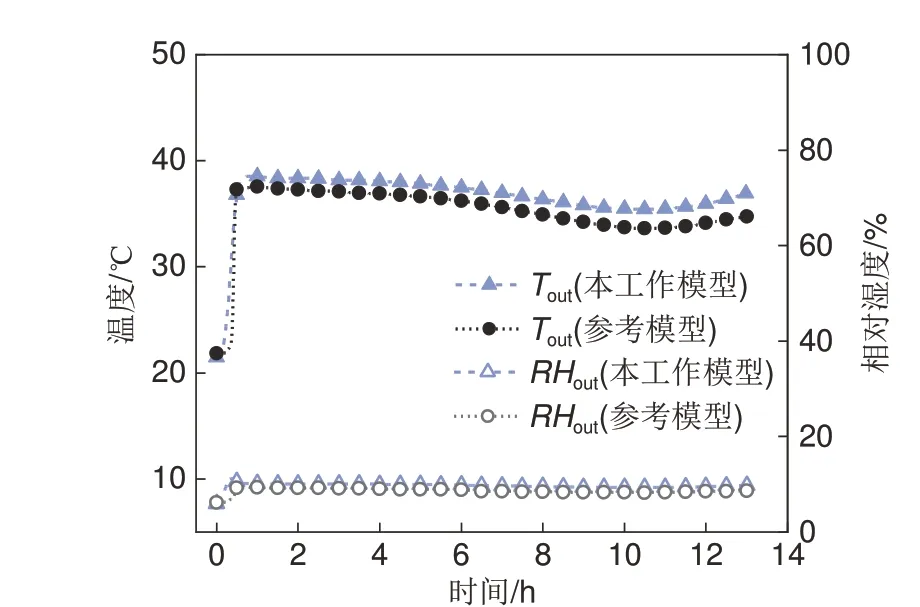
图2 水合过程模型验证Fig.2 Model validation of hydration process

合理的网格数量可以在保证模拟计算结果精度的条件下，避免计算资源的浪费，因此，对网格独立性进行检验是必要的。将5 h 的放热量作为网格独立性验证的指标。选取了50、100、150、200、250五种网格进行分析。如图3所示，随着网格数量的增加，放热量的偏差在逐渐减小，在200个网格数量上继续增加对放热量几乎没有影响，本工作最终采用200个网格作为数值模拟的网格数量。

图3 不同网格数量的放热量变化Fig.3 The change of heat output with different mesh quantities

1.5 评价指标

如图4所示，在恒定的空气入口参数输入条件下，反应器的出口空气温度会呈现先升高，再平稳输出一段时间，最后再降低到入口温度的趋势。本工作设置了以下评价指标对放热工况进行评估。

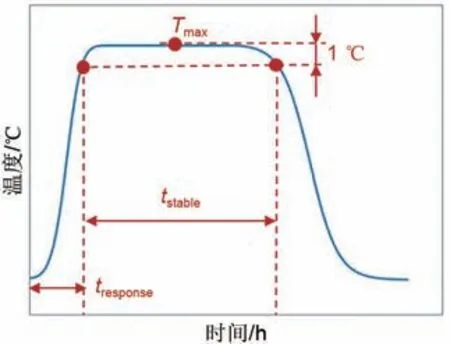
图4 评价指标示意图Fig.4 Schematic diagram of evaluation indicators

（1）出口空气温度维持在(Tmax-1，Tmax)范围内的时间，为反应器的稳定输出时间tstable。

（2）从反应开始到进入稳定状态所需时间，记为响应时间tresponse。

（3）稳定输出时间内出口空气温度的平均值与入口空气温度的差值，为空气平均温升ΔT。

（4）反应器出口的功率输出Pout，表达式为：

（5）反应器在稳定输出时间内的总放热量Qz，其表达式为：

2 参数敏感性分析

2.1 模拟参数

为了探究各参数对反应器放热性能的影响，选择了入口空气温度、入口空气水蒸气分压力、流速和反应器长度共4个参数进行分析。变化其中一个参数时，控制其他参数为基准值，具体的参数值如表1所示。

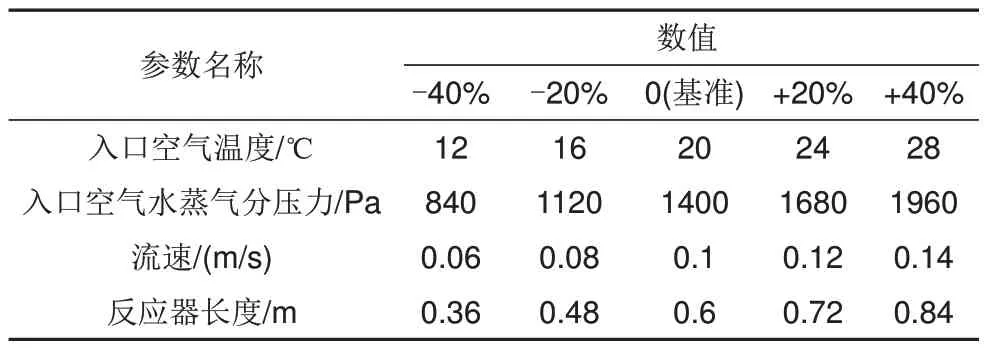
表1 敏感性分析参数设置Table 1 Parameter settings of sensitivity analysis

本工作引入敏感系数用于描述模拟结果对某参数的敏感度[13]，其表达式为：

式中，λ1为指标变化率，λ2为因素变化率。

2.2 入口空气温度的影响

图5展示了反应器空气出口温升随入口空气温度的变化。可以看到，随着空气入口温度的增加，空气平均温升和功率会降低，响应时间基本保持不变，稳定输出时间和总放热量会升高。这种现象可以用反应动力学方程进行解释，当温度升高时，反应速率会下降，因此温升和功率就会降低，总的反应时间就会增加，稳定输出时间也会增加。由于温升下降的幅度没有稳定输出时间上升的幅度大，总放热量升高。总而言之，各个因变量对空气入口温度敏感系数：稳定输出时间＞平均温升＞功率＞总放热量＞响应时间。

图5 不同入口空气温度下反应器出口温升随时间的变化Fig.5 The variation of outlet temperature rise with time under different inlet air temperature

2.3 水蒸气分压力、流速和反应器长度的影响

如图6(a)～(e)所示，将各参数变化对评价指标的影响进行分析。本工作采用4个层次的敏感系数对其进行分析：敏感系数值(-0.1，0.1)、(0.1，0.5)、(0.5，1)和(1，∞)依次用“0”“Ⅰ”“Ⅱ”和“Ⅲ”表示；若敏感系数小于0，则在前加上“-”。将整理后的结果汇总于表2，可以看到，因素对指标具有正面或负面的影响，反应器长度对稳定输出时间的影响最大，对响应时间影响次之，空气流速对响应时间和稳定输出时间的影响很大，水蒸气分压力对总放热量几乎没有影响，对其他指标有一定影响。

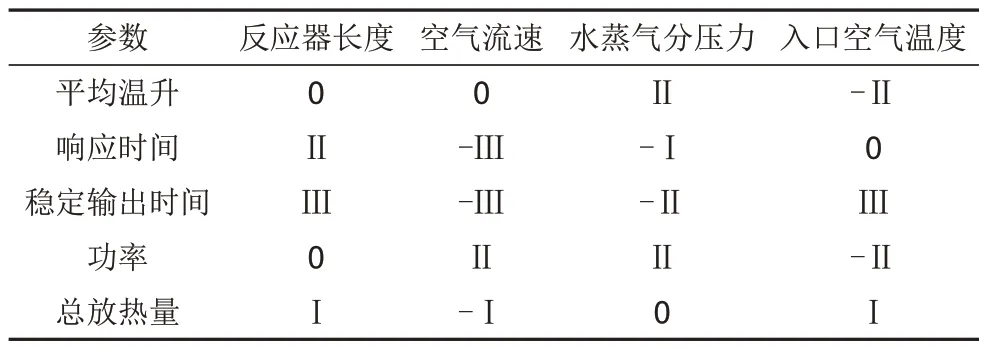
表2 敏感性分析结果Table 2 Sensitivity analysis results

图6 指标变化率 (a) 温升变化率；(b) 响应时间变化率；(c) 稳定输出时间变化率；(d) 功率变化率；(e) 总放热量变化率Fig.6 Change rate of indices (a) temperature rise; (b) response time; (c) stable output time; (d) power;(e) total heat release

3 案例分析

3.1 应用场景介绍

采用热化学反应器用于冬季供暖。假定反应器中的储热材料在供暖前完全脱水，在冬季水合释放热量，对建筑进行空间供暖。本案例的供暖对象是位于长沙市的一座三层住宅建筑(28.1°N，112.9°E)，建筑采暖面积为221 m2，层高2.2 m，建筑围护结构参数如表3所示。为了合理对反应器进行选型，需计算此栋建筑的热负荷。本工作采用EnergyPlus建立负荷模型，模拟计算长沙地区该建筑的负荷情况。

表3 建筑围护结构参数Table 3 Building envelope structural parameters

将以上参数输入EnergyPlus 软件中，可以计算得到采暖季逐时热负荷。选择12月20日作为典型天进行全天的放热工况模拟，当天的总热负荷为24.05 kWh。图7 是典型气象年12 月20 日0 时至24 时的环境温湿度变化。在14 时温度达到最高值11.4 ℃，在21时和24时达到最低值8.8 ℃。

图7 12月20日环境温度与相对湿度Fig.7 Environmental temperature and relative humidity on December 20th

反应器的能量密度为239.4 kWh/m3，假定反应器中盐处于完全脱水的初始状态，使用全天室外空气的逐时参数作为输入，出口空气参数作为输出。由于室内设定温度为18 ℃，有部分反应热用于将空气加热至18 ℃，超出18 ℃的部分才能为室内提供热量。考虑到室外空气温度与热负荷的大小，选择的反应器尺寸为1 m×1 m×0.5 m(长)。设置流量最大值为720 m3/h。

从上文有关放热阶段的敏感性分析中可以看出，空气入口湿度和流速对放热功率具有较大的影响。因此，本工作采用了湿度控制和流量控制两种控制策略，来获得合适的空气出口温度和放热功率。

3.2 控制策略

湿度控制策略如下，根据反应器出口空气温度值判断是否对入口空气进行加湿：

（1）如果出口空气温度Tout≤25 ℃，则对空气进行加湿，加湿后为100%相对湿度；

（2）如果出口空气温度Tout≥30 ℃，则不对空气进行加湿；

（3）如果出口空气温度Tout＞25 ℃且Tout＜30 ℃，则维持原状态不变。

流量控制策略如下，设定流量qs为0～720 m3/h，每间隔36 m3/h设置一个档位，共21个档位，同时每小时调整一次档位。0 h时设置为最大流量，其余时刻根据空气出口温度和室内设定温度的温差与下一小时的热负荷之间的关系来确定空气流量档位，流量q取设定流量中大于参考流量qc的最小值，若qc＞qs,max，则流量q=qs,max，qc的计算公式为：

式中，Pf为热负荷，W；ca为空气比热容，kJ/kg；ρa为空气密度，kg/m3；Tout为出口空气温度，℃；Tn为室内设定温度，℃。

逐时放热功率Pg计算公式为：

式中，t为反应时间(为3600的倍数)，s。

3.2.1 无控制策略下运行结果

不采用控制策略，将流量固定为360 m3/h，对反应器的放热性能进行分析。从图8(a)可以看出，反应器的出口空气温度呈现先降低后上升的趋势，在14.72 h时达到最大值30.5 ℃。与之相反，建筑热负荷呈现出先上升后降低的趋势，这是因为凌晨环境温度低，无太阳辐射得热，下午太阳辐射强烈，环境温度较高导致的。从图8(b)可见，由于环境温度随时间先降低后升高，反应器的放热功率在预热之后也大致呈现出先降低后升高的趋势，这正好与热负荷的变化趋势相反，在0～9 h热功率满足不了热负荷的需要，在10～24 h热功率远超热负荷。放热总量为29.32 kWh，负荷总量24.05 kWh，偏差达到21.9%。热负荷与放热功率间的平均绝对偏差为527.49 W，平均相对偏差为69.21%。

图8 不采用控制策略 (a) 空气入口与出口参数；(b) 功率与负荷Fig.8 Without control strategies (a) Air inlet and outlet; (b) Power output and thermal load

3.2.2 采用流量控制策略下运行结果

将流量控制策略应用于反应器运行过程中，可以看到图9(a)中，反应器出口空气温度与无控制策略下空气出口温度变化曲线相似，空气出口相对湿度也是维持在8.4%左右。如图9(b)所示，在采用流量控制策略后，放热功率与热负荷的偏差缩小。计算结果显示，反应器的有效放热量为25.71 kWh，比负荷总量仅高出6.9%，功率与负荷的平均绝对偏差为82.08 W，平均相对偏差为9.89%。

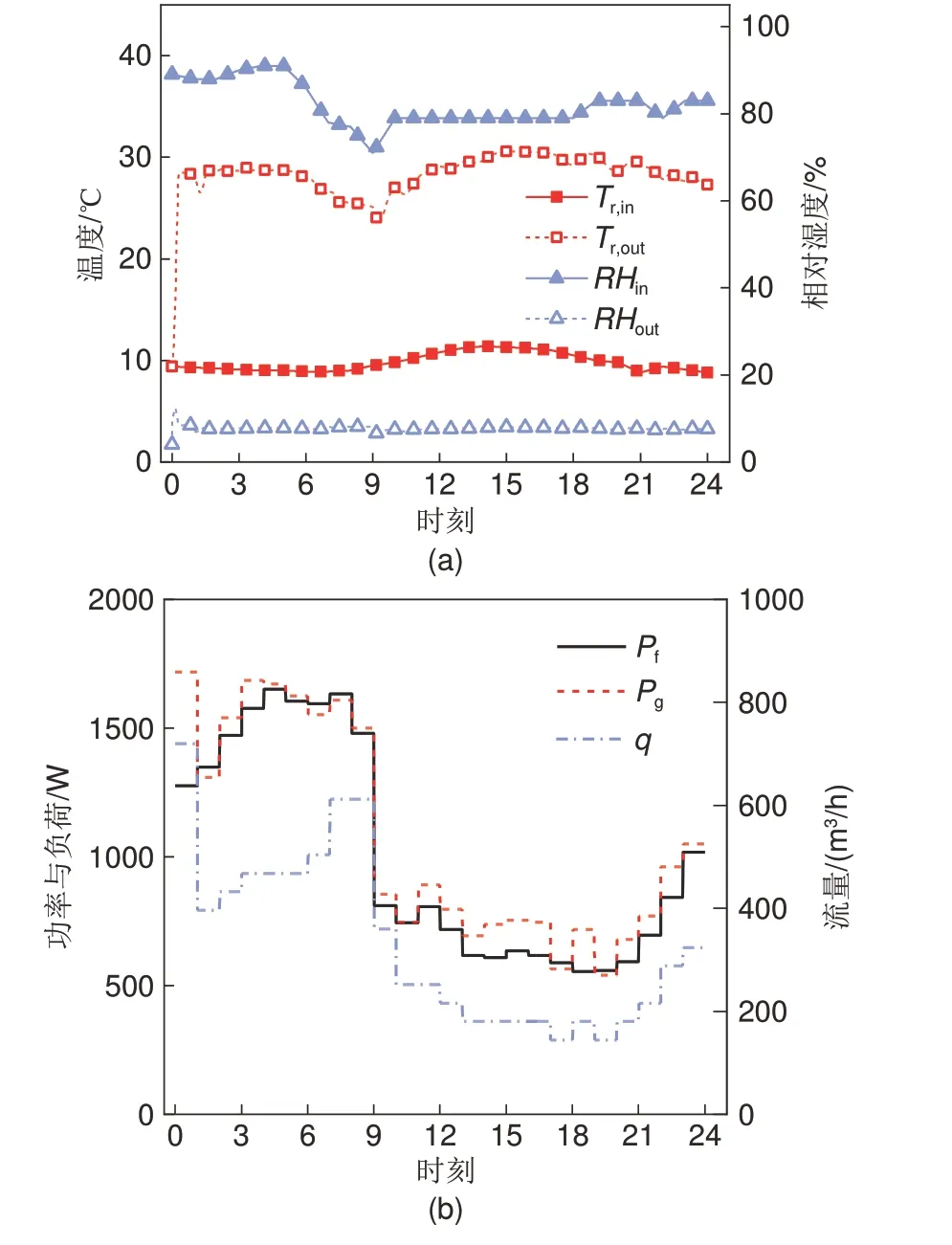
图9 采用流量控制策略 (a) 空气入口与出口参数；(b) 功率与负荷Fig.9 With flow control strategies (a) Air inlet and outlet; (b) Power output and thermal load

3.2.3 采用湿度与流量耦合控制策略下运行结果

如图10(a)所示，采用湿度与流量耦合控制策略后，分别在0 h和9 h左右对入口空气进行加湿，这是由于在这两个时刻，反应器的空气出口温度低于25 ℃。如图10(b)所示，在耦合控制策略下，反应器的有效放热量为26.24 kWh，比负荷总量高9.1%，放热功率与热负荷的平均绝对偏差为112.06 W，平均相对偏差为13.35%。

图10 采用湿度与流量耦合控制策略 (a) 空气入口与出口参数；(b) 功率与负荷Fig.10 With flow and humidity control strategies (a) Air inlet and outlet; (b) Power output and thermal load

3.2.4 三种运行模式对比如图11 所示，与无控制策略相比，采用控制策略可有效提高反应器放热功率与热负荷间的匹配率。而采用湿度与流量耦合控制策略的效果不如仅采用流量控制策略，原因在于根据空气出口温度值确定了空气流量后，如再对入口空气进行加湿或停止加湿，会导致空气出口温度升高或降低，从而使放热功率与热负荷之间差值增加。

图11 三种运行模式下功率与负荷差值Fig.11 Difference between power and load in three operating modes

4 结 论

本工作通过数值模拟的方法研究了以溴化锶为储热材料的热化学反应器的动态放热工况，将建立的数值模型与现有模型进行比较，水合工况下温度的平均相对误差为4.36%，相对湿度的平均相对误差小于12.52%，证明模型具有良好的准确性。基于以上模型，对入口空气温度、水蒸气分压力、流速和反应器尺寸等因素对出口参数的影响进行了敏感性分析。以长沙某三层建筑为例，探索了提高反应器放热功率与建筑热负荷匹配度的控制策略。主要结论如下：

（1）空气流速对响应时间、稳定输出时间和放热功率的影响较大，水蒸气分压力对温升有较大影响但对总放热量几乎无影响；反应器长度对响应时间、稳定输出时间和总放热量有影响而对温升和放热功率几乎无影响；入口空气温度对温升、稳定输出时间和功率影响较大，在实际应用中，入口空气温度越高，出口空气温度也会越高，供暖效果更好。

（2）无控制策略时，在典型日动态环境参数条件下，反应器的放热总量与负荷总量的偏差为21.9%，放热功率与热负荷的平均相对偏差为69.21%。

（3）采用流量控制策略时，典型日工况下放热总量和负荷总量的偏差为6.9%，放热功率与热负荷的平均相对偏差为9.89%。

（4）采用湿度与流量耦合控制策略时，相比无控制策略可以极大地减少放热量与负荷总量、放热功率与热负荷之间的差距，但相比只采用流量控制策略的匹配效果会稍差，这是由于反应器出口参数变化的滞后性与调节频率较小导致的，在后续研究中会对策略的约束条件进行优化。

本工作建立了适用于长时间尺度模拟的水合盐热化学反应器动态仿真模型，并初步探索了其在实际应用中的放热供暖性能。由于只对冬季典型日的放热工况进行了分析，反应器中盐的初始状态设置与实际情况存在一定偏差，在后续对整个采暖季放热工况或跨季节储热与放热的研究中需对这一条件进行调整与优化。