基于双延迟深度确定性策略梯度的卫星远程变轨控制

邱鹏鹏　张易诚　曹海涛　郑君铮

关键词：变轨控制；相对运动；目标轨道；深度强化学习

中图分类号：TP183 文献标识码：A 文章编号：1006-8228（2023）11-90-04

0 引言

近年来，随着航天技术的发展，航天器相对距离控制已成为一个活跃的研究领域，被广泛应用于卫星在轨维护、卫星组装[1]，以及空间碎片捕获[2]等多个场景，航天器相对距离控制要求卫星能够自主、安全地接近后者到达目标位置。通常，相对距离控制可分为近程控制和远程控制。近程控制一般要求探索卫星从几十公里内直接开始搜索目标[3]，而远程控制一般需要协调地面站，获取目标位置，从而引导探索卫星变轨到近程轨道。解决远程相对距离控制问题需要制定合理的变轨策略，然而这往往面临着许多困难。由于空间飞行环境多变且复杂，因此任务实现难度异常艰巨，代价巨大。传统的基于优化控制的方法，其有效性取决于动态模型的准确性，如果因环境不稳定等因素导致的引导模型的精准度不足，那么飞行任务则极易失败。因此，需要使用健壮且具有较强自适应能力的策略以应对各类空间飞行问题。

深度强化学习（DRL）是机器学习领域的一个热门研究课题。智能体根据自身状态及其他已知信息做出相应的动作，通过与环境的交互作用来获取奖励，不断优化策略指引智能体向奖励高的方向行动，直到获得最优策略。因此，一方面DRL 代理能够降低计算频率，这使得其广泛应用于具有有限计算能力的卫星上；另一方面通过减少代理自主性对优化方法的依赖从而降低行为间相关联性。

针对以上方法及問题，提出一种基于深度强化学习双延迟深度确定性策略梯度算法（Twin DelayedDeep Deterministic Policy Gradient Algorithm，TD3），从而解决在复杂多变的连续空间环境下的变轨任务。具体来说，通过引入合适的数据处理方式、设置合理的奖励函数，令卫星与环境不断进行交互，进而引导卫星做出点火决策的同时更新策略，并最终从高轨道逐步变轨到达目标轨道附近。最后，利用可视化方法验证TD3 算法解决卫星相对距离控制问题的有效性。本文的贡献是：①考虑卫星真实情况下间断性点火特性，解决了在算法控制与状态变化不同频率状况下的卫星椭圆轨道变轨控制；②引入轨道动力学模型，采用动态Z-score 数据处理方法，提出了一种TD3 控制算法，，有效地解决了高轨道、高维度下卫星变轨问题。

1 背景及现状

随着航天技术的快速发展，卫星变轨控制引起越来越多的学者关注，这使得变轨飞行可行性和关键性技术被充分挖掘，许多方案都取得了良好的效果。

卫星变轨到达目标轨道的问题，本质上是一种相对距离协调控制问题，国际上目前常见的卫星相对距离飞行控制方法包括系绳法、库仑力法[4]、人工势函数法[5]、李亚普诺夫函数法等。在库仑力卫星控制中，采用一定的技术手段使得卫星带电（正电荷或负电荷），通过控制卫星带电量来控制卫星受力大小及方向，进而实现卫星变轨到达目标轨道。库仑力法解决了卫星近距离相对距离控制时设定卫星同性电荷从而避免发生碰撞。然而，库仑力法受到卫星间的间距限制，它无法支持远程卫星引导控制。

深度强化学习在解决复杂的非线性控制问题方面具有很大的优势，因此常被用于处理航天领域的相关研究。为了实现卫星的交会对接，作者引入近端策略优化算法（Proximal Policy Optimization，PPO），设定防碰撞区域以及安全区域，结合相对轨道的动力学方法[6]。为了解决近距离的航天器对接问题，介绍了一种能够在真实航天器平台上使用的基于分布式深度确定性策略梯度的算法[7] （Distributed DistributionalDeep Deterministic Policy Gradient，D4PG），用于拟合出最佳制导轨迹从而反馈到常规控制器上以进行卫星轨迹跟踪。然而，上述基于深度强化学习的卫星变轨控制策略大都基于卫星间距仅为几千米的范围，目前针对卫星远程相对控制的文章少之又少。因此，本文将采用TD3 算法来解决卫星在椭圆轨道变轨下到达目标轨道问题。

4 仿真实验及结果分析

4.1 实验环境及参数

实验中，卫星和地球的半径分别90km、6371km，质量分别为4474kg、5.965E24kg。

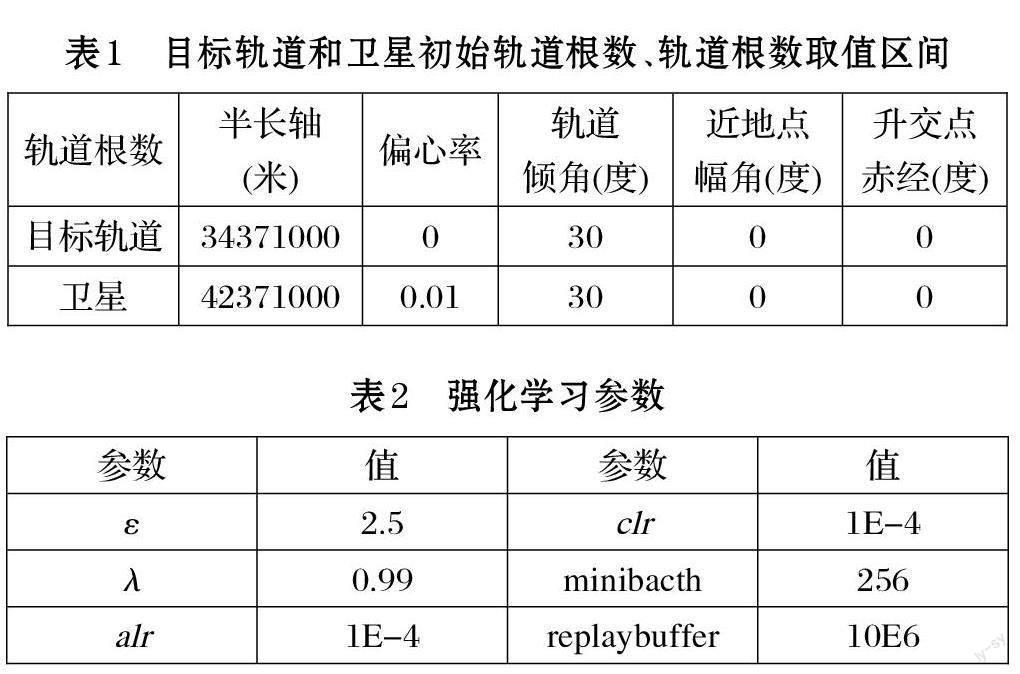
卫星轨道根数半长轴、偏心率、轨道倾角、近地点幅角、升交点赤经取值范围分别为[6.371E3，3.6E7]、[0，1]、[0，π]、[0，π]、[0，2π]。初始化目标轨道和探索卫星的轨道六根数如表1 所示。设定卫星初始真近点角为0，则可以计算出卫星的初始位置矢量和速度矢量分别为：（3.02E7，0，1.91E7）、（0，2798.17，1615.52）；同时，可以计算出目标轨道加速度和速度大小分别为：0.34m/s^2、3403.32m/s。我们设定卫星点火作用时间为一秒钟，依据网络输出的动作，可计算出相应的速度变化量和位置变化量。同时，在下一次点火动作到来之前，卫星受万有引力作用自由飞行五分钟。

定义神经网络为三层全连接层，即5*128*128*3。神经网络状态输入为卫星轨道根数，网络输出为三轴方向的加速度，其取值范围为[?10m/s^2，10m/s^2]。同时，TD3 算法中参数具体设置如表2 其中，ε表示高斯噪声的均方误差，λ 表示式⑺中的目标函数折扣因子，alr 和clr 分别表示Actor 网络与Critic 网络的学习率。minibacth 表示从replaybuffer 采样的最小单元。同时将噪声切割的上下限c 设置大小为5。

在奖励设置中，奖励系数α₁，α₂，α₃，γ₁，γ₂分别为20，10，10，100，100， 而βi = 15， i = 1…5。奖励函数设计为偏差的一次反比例函数。

4.2 结果分析

在本文中，我们设定卫星距离目标轨道500 米以内即判定系统收敛。经过TD3 算法引导，系统产生的奖励与轨迹图分别如图1 和图2 所示。从图1 中看出系统在约300 步左右就收敛，系统奖励值收敛在-1E-5附近。从图2 中可以看出卫星从开始位置逐渐变轨到终点位置从而到达目标轨道（更浅色的圆）附近。

我们同样利用TD3 算法与DDPG 算法进行实验，如图3 所示。对比图3（a）可以看出，经过了Z-score 数据处理过的网络更加稳定，也更加适用于处理像卫星这样各数据量级不在同一量级上的问题；而对比图1与图3（b）易看出，我们所提出的基于Z-score 的TD3算法相较DDPG 算法具有更快的收敛特性。

5 总结

本文提出在深度强化学习下的TD3 控制算法，来处理卫星通过远程变轨到达指定目标轨道的问题。实验结果表明，该算法能够有效解决卫星变轨到达目标轨道的控制问题。然而在本算法中，并未考虑多颗卫星情况，真实空间任务多是基于多卫星完成的，接下来考虑多个卫星在强化学习作用完成到达目标轨道任务。