基于GPU并行加速变压器二维瞬态流场问题的研究及应用

任增强， 刘 刚， 靳立鹏， 武卫革

(1.河北省输变电设备安全防御重点实验室(华北电力大学)，河北 保定 071003；2.保定天威保变电气股份有限公司 河北省输变电装备电磁与结构性能重点实验室，河北 保定 071056)

0 引 言

油浸式电力变压器作为电网关键设备之一,确保其安全稳定工作对电网的安全稳定运行具有重要意义[1,2],而热点温升是衡量变压器安全稳定运行的一个重要指标。计算油浸式电力变压器瞬态温升问题涉及电磁场、流体场和温度场,是一个多物理场耦合计算问题[3-5],包括热源(即损耗)的确定、油流和温升的分布。在计算二维油浸式电力变压器瞬态多场耦合问题时,流体场网格较密,方程自由度较大,方程求解耗时较长,同时由于是瞬态问题,在各时刻的逐场迭代求解过程中都要先对流体场迭代求解,因此流体场求解次数多,整个耦合仿真的计算耗时主要在求解流体场这一部分,所以提高流体场计算效率对加速求解油浸式电力变压器的瞬态多场耦合问题具有重要意义。

流体场常用数值计算方法有:有限体积法、有限元法和有限差分法。有限体积法守恒性好,但对于边界条件需单独处理,增大工作量[6]。文献[7]采用有限体积法计算了油浸式变压器二维流体场—温度场,在模型和参数简化的前提下获得了温度和热点的分布。有限元法的网格剖分灵活,对边界条件无需单独处理。有限差分法离散形式简单,但对网格的划分要求严格。文献[8]结合了有限差分法和有限元法,对变压器三维温度场进行数值计算,提高了计算精度。文献[9]基于有限元计算了变压器流体场—温度场,并充分考虑油道结构对绕组散热的影响,进行了合理的优化。

最小二乘有限元法保留有限元法优点的同时,还能得到对称正定的稀疏矩阵,在求解流体场时数值稳定性高,并且最小二乘有限元程序编写形式统一、易于修改、通用性高。文献[10]采用最小二乘有限元法计算了二维方腔顶盖驱动流模型的瞬态解。

本文采用最小二乘有限元法对二维瞬态流体场求解,通过引入无量纲最小二乘有限元法的离散格式[10],降低刚度阵的条件数,并且采用预处理共轭梯度法迭代求解流体场在不同时刻的速度分布。

为解决计算耗时大的问题,本文基于GPU对瞬态流体场程序进行并行加速,将无量纲最小二乘有限元程序中计算量最大的两部分,即单元刚度阵的形成和稀疏线性方程组的求解[11-15],移植到GPU上运算,充分利用GPU的计算资源进行加速,大幅减少计算时间。同时,采用稀疏存储技术,以减少计算机的内存需求[17,18]。基于方腔驱动流模型验证了基于GPU并行程序的有效性,并将该GPU并行程序应用于大型变压器绕组的流体场仿真。

1 二维瞬态流体场的无量纲最小二乘有限元法

最小二乘有限元法的思路是在流体场计算问题中引入涡量ω,把Navier-Stokes方程转化为一阶偏微分方程,将构造的最小二乘泛函通过泛函变分以及数值离散得到最小二乘有限元方程。瞬态流体场的最小二乘有限元离散过程概述如下。

1.1 不可压缩流体的Navier-Stokes控制方程

在计算过程中,将变压器油密度ρ视为常量,根据质量守恒方程和动量守恒方程求得油流速度分布,控制方程可表示为[4]

▽·U=0

(1)

(2)

式中:U为速度矢量;ρ为密度;p为压力;μ为动力粘度系数;f为外力密度矢量。

将式(2)中的二阶项通过引入涡量ω转化为一阶项,得到U-p-ω耦合Navier-Stokes方程,表示如下:

ω-▽×U=0

(3)

(4)

1.2 瞬态流体场无量纲最小二乘有限元及其离散形式

参考文献[10],将基本变量变换为无量纲量,用下标带星号的符号表示,并在直角坐标系中展开:

(5)

(6)

(7)

(8)

式中:下标带星号的变量为对应的无量纲量,Re为雷诺数。

采用Crank-Nicolson方法将上述方程中的时间微分项进行离散,同时将式中非线性项进行牛顿线性化处理,可得

(9)

(10)

(11)

(12)

上式可写为如下矩阵形式:

(13)

各矩阵运算符A1,A2,A0,b以及g参考文献[13],本文不做过多赘述。

由式(13)定义残差函数:

R=A(g)-b

(14)

根据最小二乘有限元法基本原理,构造残差泛函为

(15)

对残差泛函取一阶变分得

即

(16)

对计算区域用四边形八节点单元进行剖分,选取合适插值基函数,构造各单元解ge的近似函数:

(17)

可得全离散格式的最小二乘有限元方程组统一格式如下:

KGk+1=F

(18)

式中:Gk+1是待求解向量。根据流体边界条件,即可通过式(18)获得各时刻的油流速度。上述详细推导过程请参考文献[10],本文不再赘诉。

需要说明的是,虽然最小二乘有限元法形成的刚度阵K具有稀疏、对称正定以及方程组收敛快的特点,但是相较于有限体积法或迎风有限元法,最小二乘有限元法在每个节点存在较多的待求解变量,当问题规模变大时,方程组整体阶数较大,总计算时间较长。为提高计算效率,本文拟通过GPU并行计算减小瞬态流体场计算时间,程序并行化实现过程如下。

2 基于GPU并行计算二维瞬态流体场

根据NVIDIA GPU构架特点,将无量纲最小二乘有限元程序中计算量最大的两部分,即单元刚度阵K、F的形成和稀疏线性方程组的求解[14],通过CUDA中的kernel函数调用GPU线程进行并行运算,第一部分需要调用的GPU线程数为剖分网格单元的个数,第二部分需要调用的GPU线程数为方程组的阶数。从存储格式、任务划分和线程映射对二维瞬态流体场程序进行并行加速,并结合CUDA平台编程特点在该平台完成程序的并行加速,流程如图1。

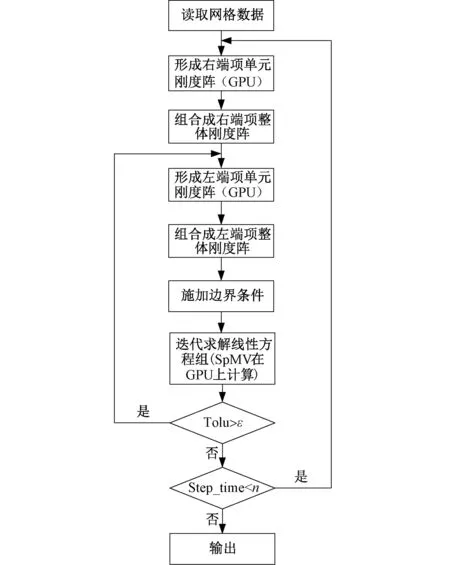
图1 瞬态流体场程序并行计算流程图Fig. 1 Flow chart of transient flow field program parallel calculation

2.1 二维瞬态流体场程序的任务划分

CPU与GPU的设计目标不同,因而在硬件内部结构上体现差异。如图2所示,CPU基于低延时设计的,内部Cache占据大量空间,大的缓存可以有效降低数据访问带来的延时,同时复杂的控制逻辑单元通过提供分支预测的能力来降低延时,CPU内部只含有少量的运算器(ALU)。GPU基于大吞吐量设计的,内部拥有大量的ALU和大量的thread来达到非常大的吞吐量的效果,而内部的缓存是为Thread提高服务而并非像CPU一样保存之后需要访问的数据,因此GPU广泛应用于密集型计算问题。NVIDIA GPU用Grid和Block来分配线程,Thread是最小分配单位。将计算问题细分成多个更小且重复执行的子问题,分配在多个线程上,以线程块的形式同步计算,减少计算耗时。

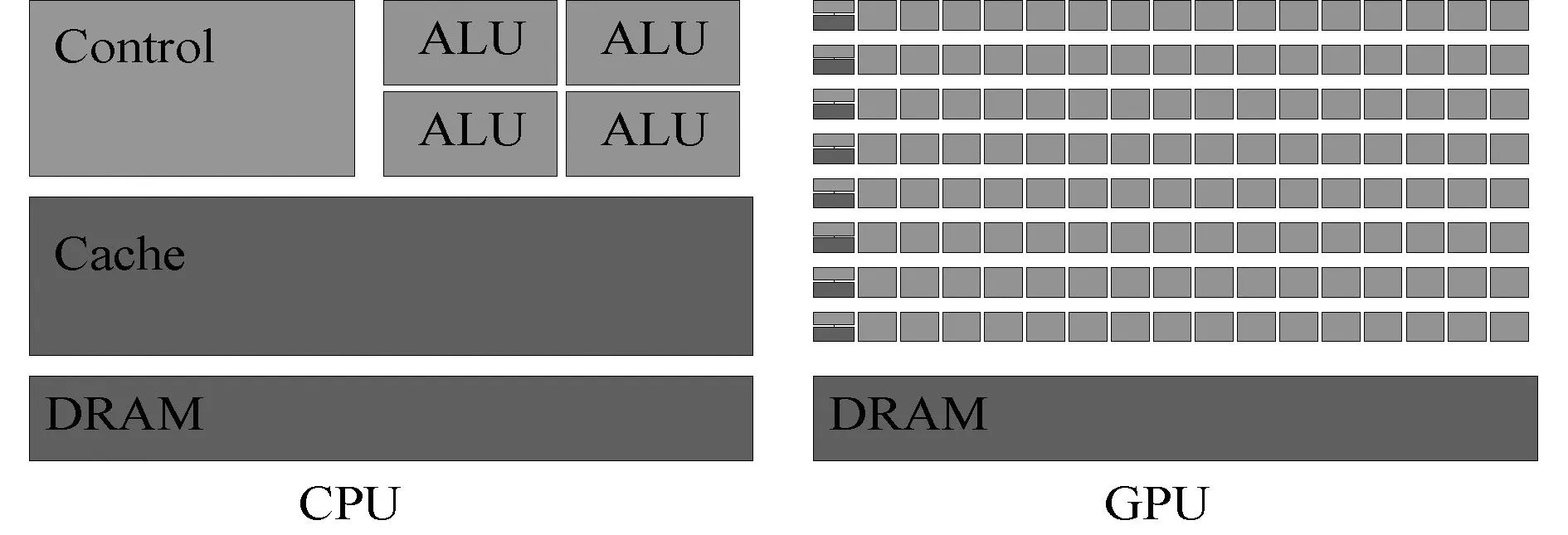
图2 CPU和GPU的结构图Fig. 2 CPU and GPU structure diagram

CUDA提供了GPU线程块调用平台,通过Kernel函数将各细化后的数据或子问题分配到GPU线程块(block)中各线程(thread)上,各线程块之间以协作的方式实现数据互通。而每个block是独立自主的以任何次序去运行的。

在二维瞬态流体场程序中,通过Kernel函数调用与流体区域单元数相匹配的线程数,将各单元刚度阵的形成在多个线程块上同时执行,__global__ void youduanxiang和__global__ void gangduzhen 两个函数分别执行右端项列向量F和左端项单元刚度阵K的并行计算。需要注意的是,在调用线程时,是以线程块为单位去选择各线程块上的线程数,所以计算调用的线程数要大于等于流体区域的单元数。同时由于内核函数的启动是异步的,所以在形成整体刚度阵之前,需要通过调用cudaDeviceSynchronize()函数实现kernel函数的同步。

2.2 稀疏矩阵的存储格式

在形成单元刚度阵时,首先采用三元组(COO)的格式来记录单元中各节点的物理量以及该值在整体刚度阵中的横、纵坐标,然后在形成整体刚度阵时,因为整体刚度阵具有稀疏性,如果通过形成满阵的方式去形成整体刚度阵,则会浪费大量的内存去存储矩阵中的零元素,随着模型规模的增大会发生内存不足的情况,因此,本文采用十字链表法形成整体刚度阵,然后采用更适合并行计算的Compressed Sparse Row (CSR)格式存储整体刚度阵。

十字链表是一种链式存储结构,采用动态存储分配,不会造成内存浪费和溢出,不存在空间的限制。图3(a)为十字链表存储稀疏矩阵非零元素的示意图,图3(b)为链表中节点结构图,两个指针域分别指向该行下一个非零元素以及该列下一个非零元素。

将单元刚度阵中行、列坐标相同的物理量进行相加,如图4,通过十字链表的方式去形成整体刚度阵,在提高存取效率的同时也大大降低了内存需求。

图4 十字链表形成整体刚度阵Fig. 4 Form an integral stiffness matrix by cross chains

相较于十字链表格式,CSR更适合于矩阵向量乘操作,因此本文最后采用CSR格式存储刚度阵非零元素,需要三个数组:

sra_k—用来存储矩阵中非零元素的值;

clm_k—第i个元素记录了sra_k[i]元素的列号;

fnz_k—第i个元素记录了第i行元素在sra_k数组的位置,在数组最后补上矩阵非零元素的个数。

图5(a)为矩阵k的CSR存储示意图,图5(b)为矩阵k与向量p相乘。

图5 矩阵Fig. 5 Matrices

2.3 稀疏线性方程组的迭代求解

因为线性方程组的系数矩阵是对称正定的,因此采用预处理共轭梯度法(PCG)求解。对稀疏矩阵进行预处理来降低其条件数,以提高方程组计算的收敛性,更好地改进共轭梯度法的收敛性。PCG方法计算过程中SpMV耗时占了超过80%的计算总时间,如图6所示,用__global__ void SpMV函数实现SpMV并行操作,用__global__ void Diag函数实现对角预处理共轭梯度法中对角矩阵与列向量相乘并行操作。采用GPU并行实现的方法就是使用Thread为最小分配单位来计算矩阵的某一行与列向量相乘的操作,使得方程求解也充分利用了GPU资源。

图6 矩阵与列向量相乘并行程序Fig. 6 Matrix and vector multiplication parallel programs

3 二维瞬态流体场并行程序有效性验证及性能分析

方腔几何参数参照文献[4],如图7所示,方腔模型边长L=0.1 m,方腔模型上边界施加恒定向右的速度,其余边界速度为0,材料特性:ρ=1 000 kg/m3,μ=0.25 Pa·s。并进行如下假设:

图7 方腔模型几何图Fig. 7 Square cavity model geometry

(1) 方腔左右两侧以及底部为无滑移壁面;

(2) 初始条件为u=1 m/s,顶部v=p=0,其他边界u=v=p=0。

在求解方腔瞬态流体场的过程中,时间步长设为Δt=0.02 s,运行200个时步。

本文仿真采用的电脑CPU型号为Intel(R) Core(TM) i9—10900K CPU @ 3.70GHz,逻辑处理器个数为20。在Visual Studio 2019软件中用C语言实现二维瞬态流体场的最小二乘有限元法的串行程序。随后在NVIDIA CUDA 10.2平台上实现程序并行,GPU型号为NVIDIA Quadro P2200。

3.1 串并行程序有效性验证

串行程序与GPU并行程序对方腔模型进行计算,第两百个时步已达到稳态,获得的流体场分布如图8(a)、(b)所示,为验证串、并行程序的有效性,本文采用Fluent软件对该模型进行仿真,其流体场分布如图8(c)所示。

图8 流体场分布云图Fig. 8 Flow field distribution cloud diagrams

由图8可知,基于无量纲最小二乘有限元的串、并行程序计算结果与Fluent软件仿真结果得到的流体场分布云图趋势基本一致,无明显差异。为了进一步说明串、并行程序的准确性,提取方腔模型中心点(x=0.05 m,y=0.05 m)随时间变化的速度模值以及第两百个时步模型竖直中心线(x=0.05 m)上各点的速度模值,并绘制成曲线,如图9和10所示。

由图9可知,串行、并行程序和Fluent软件计算出方腔模型中心点速度模值的趋势均为先增大后减小,并且在2.5秒左右趋于稳定。串行、并行程序计算结果吻合完好,第4秒程序计算中心点的速度模值为0.122 4 m/s,Fluent软件计算结果为0.119 8 m/s,相对误差为2.2%,精度满足要求。由图10可知,串、并行程序的计算结果与Fluent软件计算结果基本一致,验证了串、并行程序的有效性。

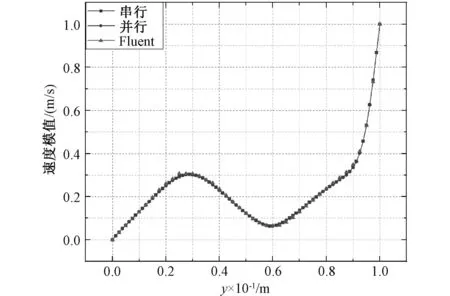
图10 中心线上各点速度模值Fig. 10 Velocity of each point on center line

3.2 十字链表稀疏存储对内存消耗影响分析

本文采用十字链表法形成瞬态流体场程序的整体刚度阵K,为探究该方法与通过形成满阵来形成整体刚度阵的方法相比,对数据存储内存消耗的影响,对于图7的方腔模型,本文采用十种不同规模的剖分网格,分别计算出使用十字链表法和满阵法时整体刚度阵所占内存,如表1所示。

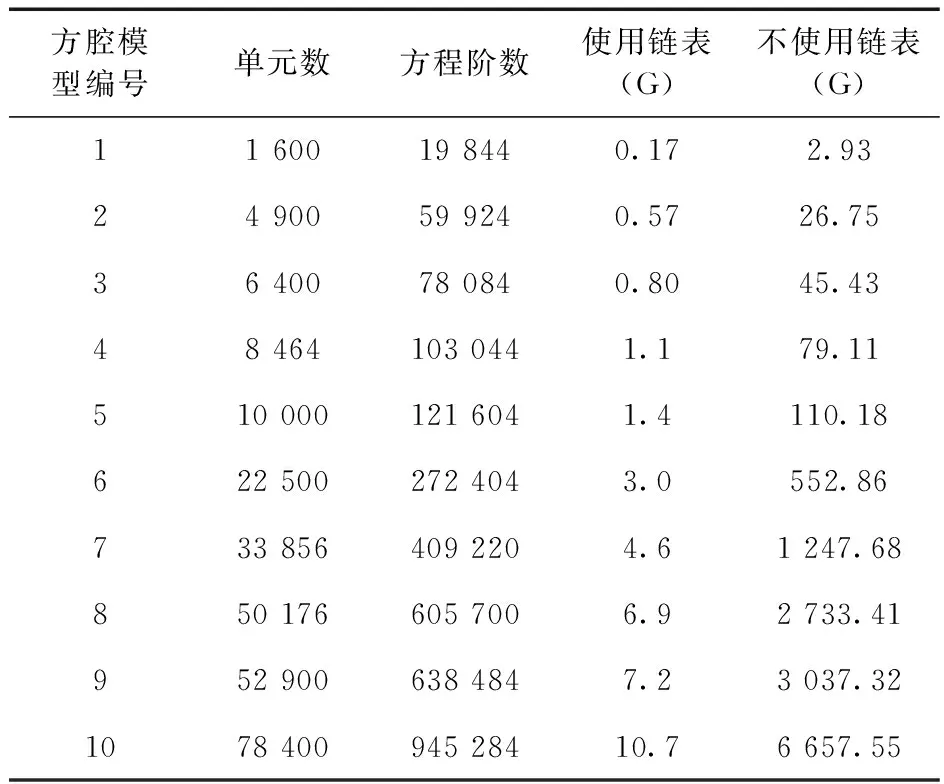
表1 是否使用十字链表所用内存

由表1可知,采用十字链表法之后,整体刚度阵对内存的需求大幅度降低,减少了计算机读取数据的时间。在实际工程问题中,模型规模越大,最小二乘有限元形成的整体刚度阵的阶数也随之增大,若不采用十字链表法形成整体刚度阵,则计算机内存将无法满足要求。

3.3 不同网格规模的并行程序加速比

为了比较串行程序与并行程序在计算流体场时的耗时以及加速比,分别对表1中10种不同规模下的方腔模型进行求解,记录程序求解第一个时间步Δt=0.02 s流体场问题所需要的时间,如图11(a),并比较各规模的加速比,绘制出曲线如图11(b),各数据如表2所示。

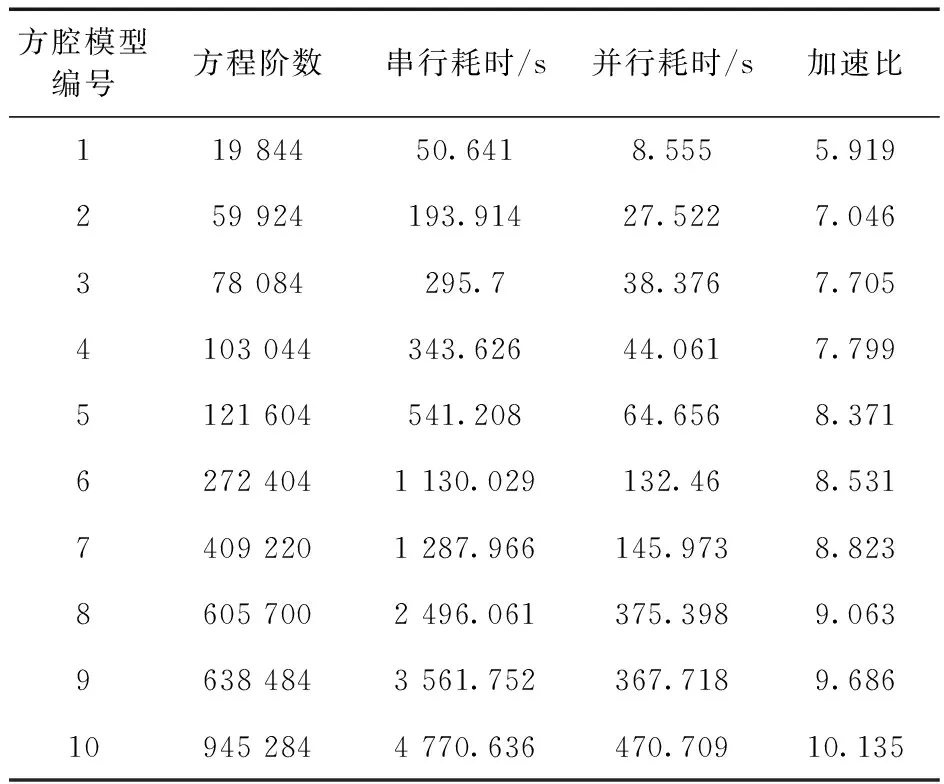
表2 串行、并行程序耗时及其加速比

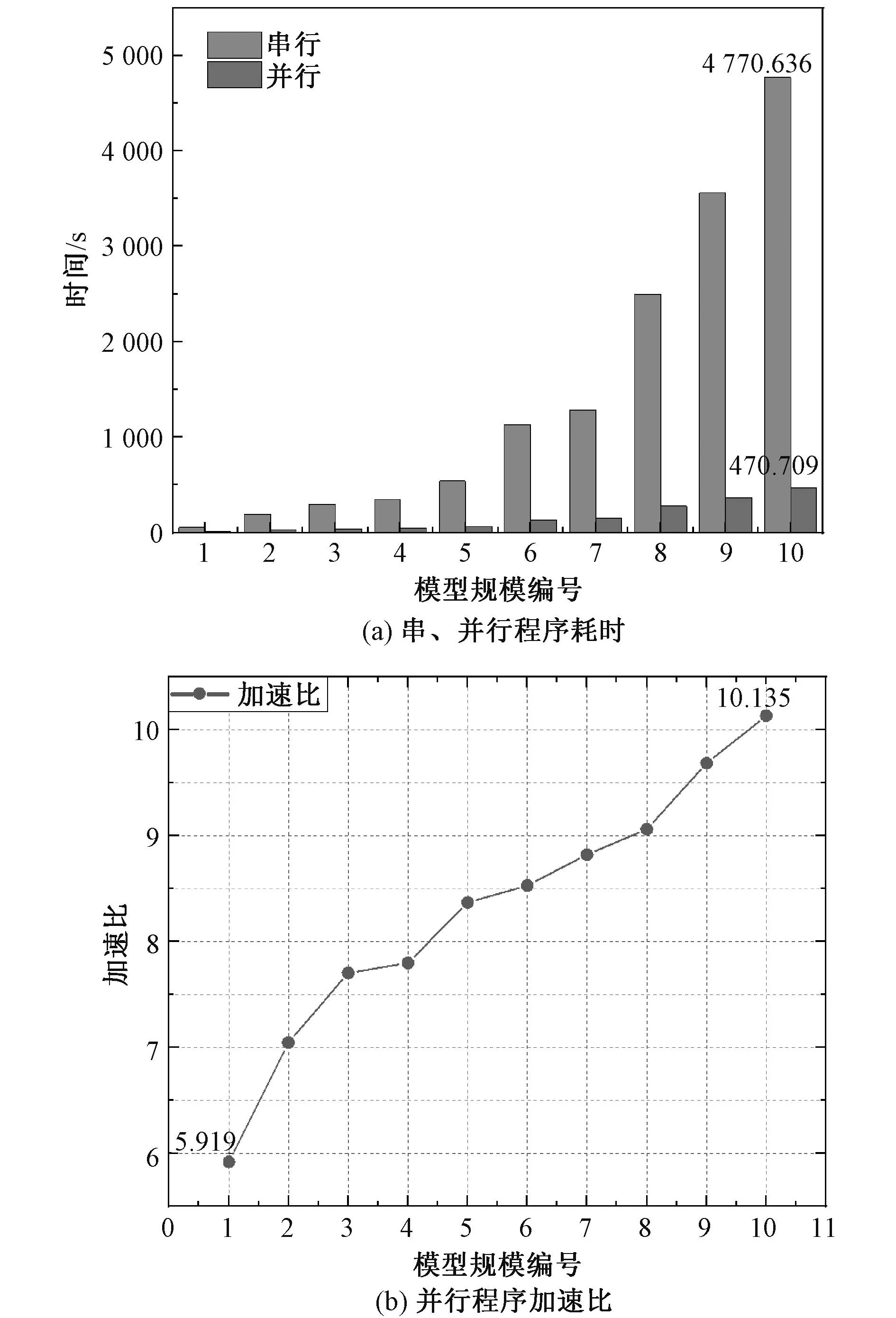
图11 串并行计算效率对比Fig. 11 Comparison of efficiency of serial parallel computing

由表2和图11(a)可知,网格剖分越密,计算流场形成刚度阵的阶数越大,串、并行程序在求解流场时消耗时间增加。定义加速比=串行程序耗时/并行程序耗时,由图11(b)知,并行程序加速比与模型规模有关,模型规模越大,并行加速效果越显著,本文对10组方腔模型并行加速,最小加速比为5.919,最大加速比为10.135。上述实验是研究计算瞬态流体场问题在第一个时间步的耗时情况及加速比,由此可见,如果通过并行程序完成整个瞬态流体场的计算,其节省的时间将是相当可观的。

4 GPU并行加速在产品级变压器中的应用

4.1 变压器绕组模型的几何参数

本节将本文所提的二维瞬态流体场串、并行程序应用到一个大型油浸式变压器绕组流体场分析中。大型变压器整个绕组分为8个分区,从上到下编号为1～8。1号分区到3号分区各有7段线饼,4号分区到8号分区各有9段线饼,线饼从上到下编号从1到66[13]。建立变压器绕组的二维仿真模型时,将不考虑撑条和垫块,二维模型的各项尺寸参数如表3所示。

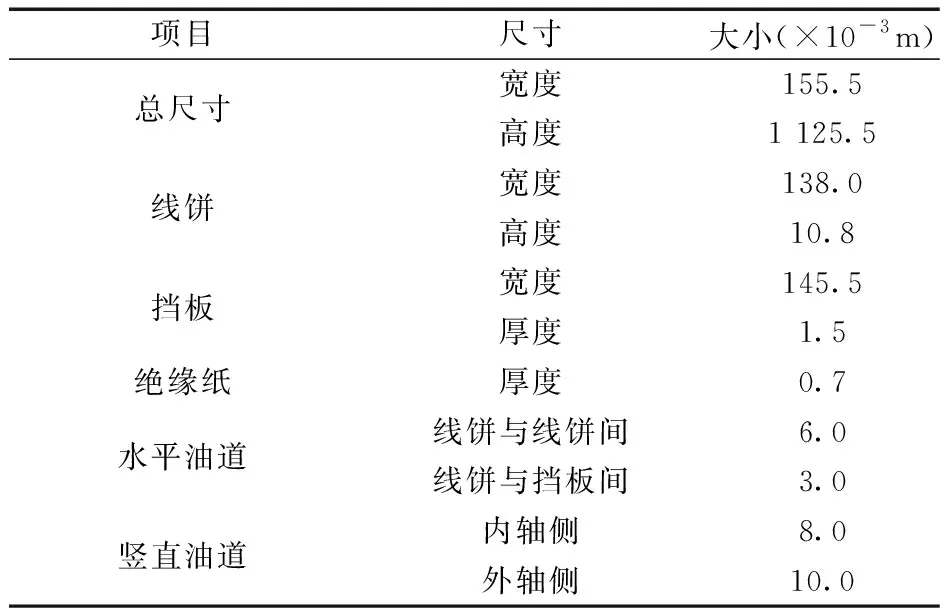
表3 绕组模型尺寸

4.2 绕组模型的物性参数和边界条件

本文在求解绕组瞬态流体场问题时,只需考虑变压器油中与流体场计算相关的各项物性参数,并且忽略变压器绕组的材料属性。变压器油的各项物性参数是温度的函数,参数见表4。

表4 材料物性参数

为了简化分析,本文假设模型的整体油温T=330 K,因此可认为变压器油的物性参数是定值。模型入口边界条件设为u=0,v=0.2 m/s;出口设置压力边界条件为u=0,p=0;绕组、垫圈以及绝缘筒为流-固耦合的无滑移的壁面边界条件,u=0,v=0。

4.3 计算结果、加速比及分析

采用二维瞬态流体场串、并行程序对上述变压器绕组模型进行数值计算,时间步长设为Δt=0.05 s。图12为第100个时步时流场分布云图。

由图12可知,串行程序和并行程序计算得到的绕组流体场分布基本一致,无明显差异。提取绕组模型第八个分区第100时步10条水平油道竖直中心线(x=0.077 75 m)上各点的水平速度模值以及第八分区由下至上第1,5,9号油道中心点水平速度模值随时间变化,并绘制成曲线,如图13和14所示。

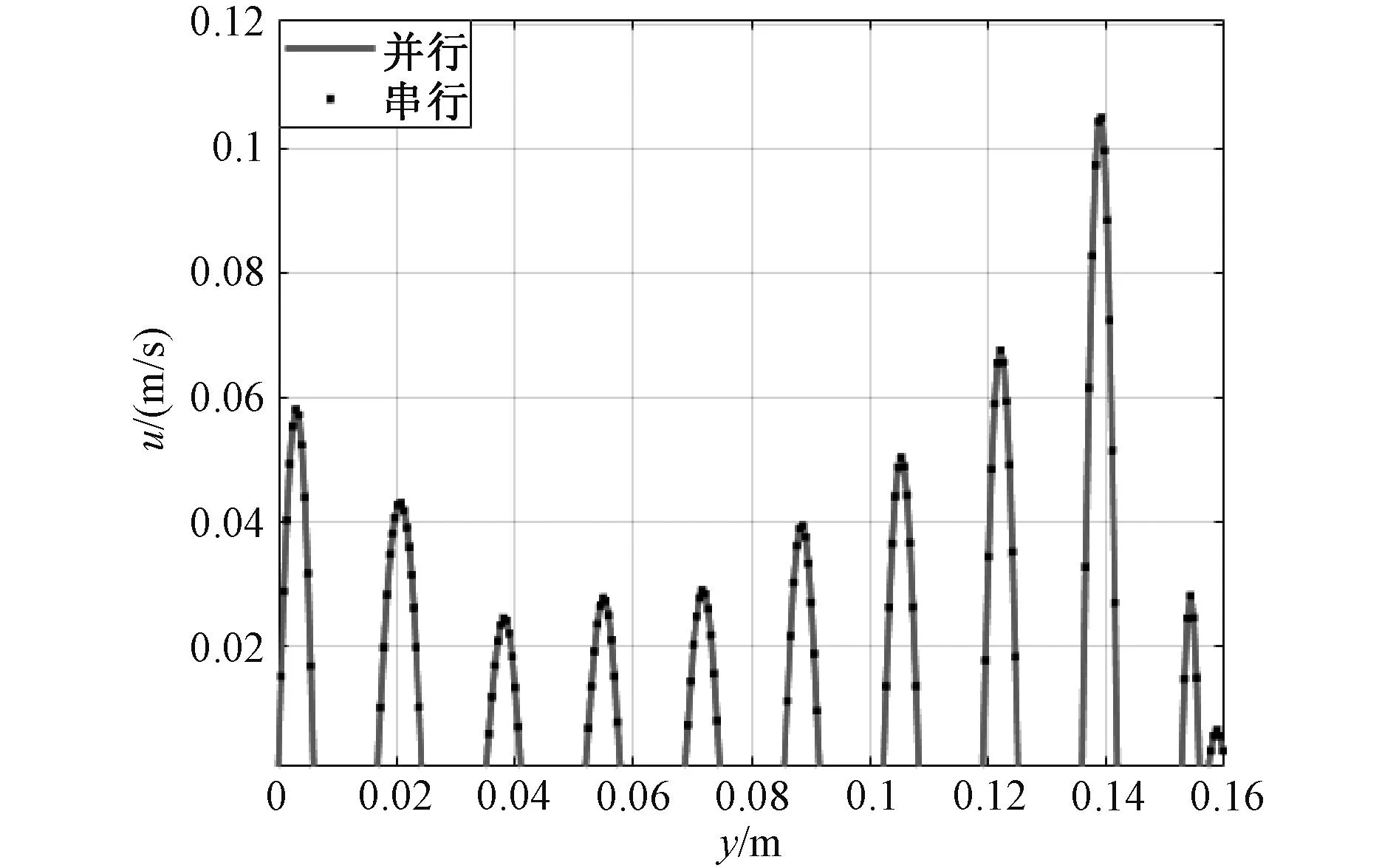
图13 中心线上各点水平速度Fig. 13 Horizontal velocity of each point on the center line

由图13可知,在第100个时步,变压器绕组模型第八分区十条水平油道油流速度的最大值出现在第九条油道,最小值出现在第三条油道。由图14可看出,1,5号油道中心点水平速度随时间先增大后减小然后趋于稳定,9号油道先增大然后趋于稳定,三条油道中心点水平速度都在2 s左右达到稳定。

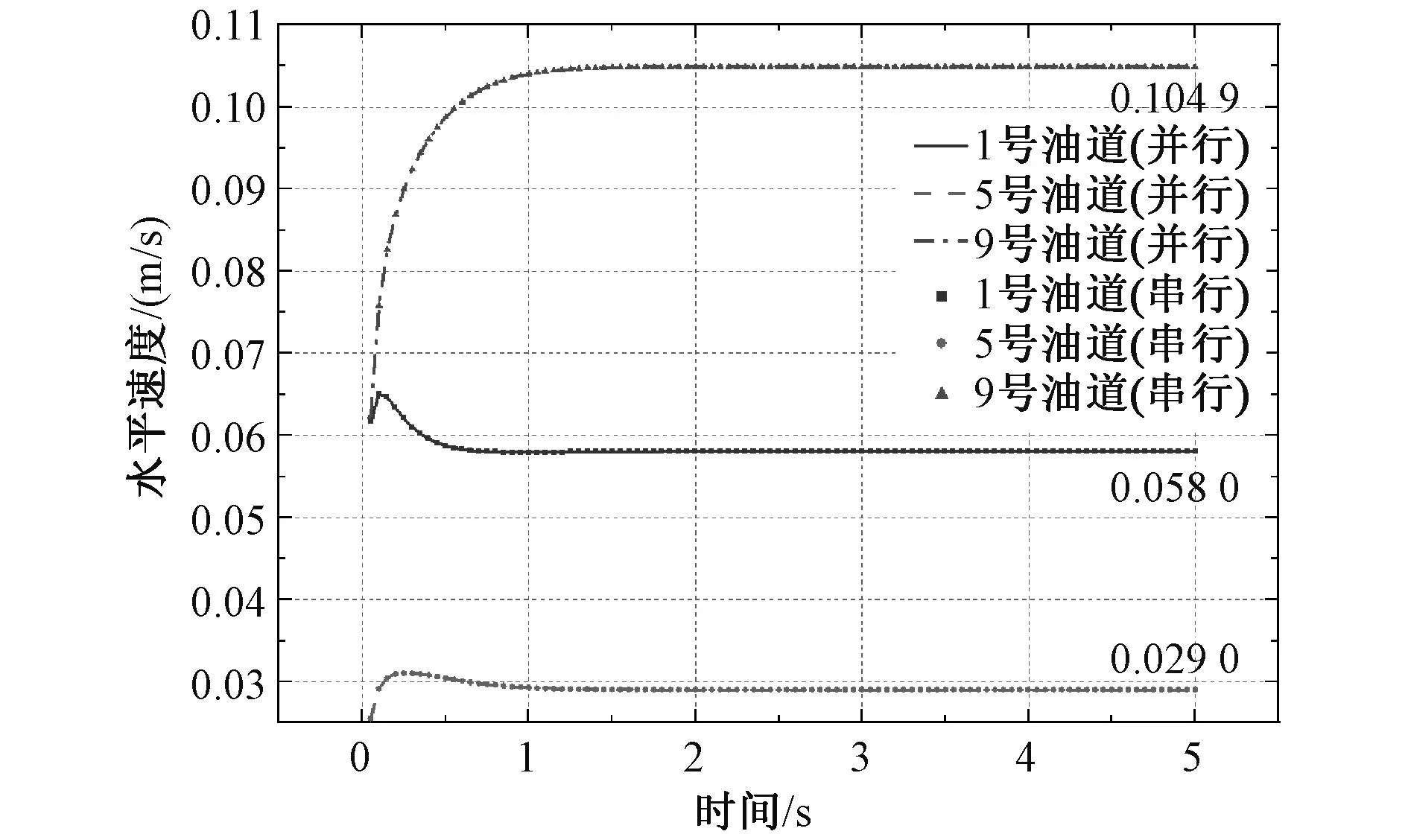
图14 1,5,9号油道中心点水平速度随时间的变化Fig. 14 Horizontal velocity change at center point of No.1, 5 and 9 oil lanes with time

进一步比较串行程序与并行程序在计算时间上的差异,记录串、并行程序计算变压器绕组模型瞬态流体场前20个时间步所用时间、每个时间步内方程求解次数并计算每个时间步内的加速比,绘制出曲线图,如图15所示。

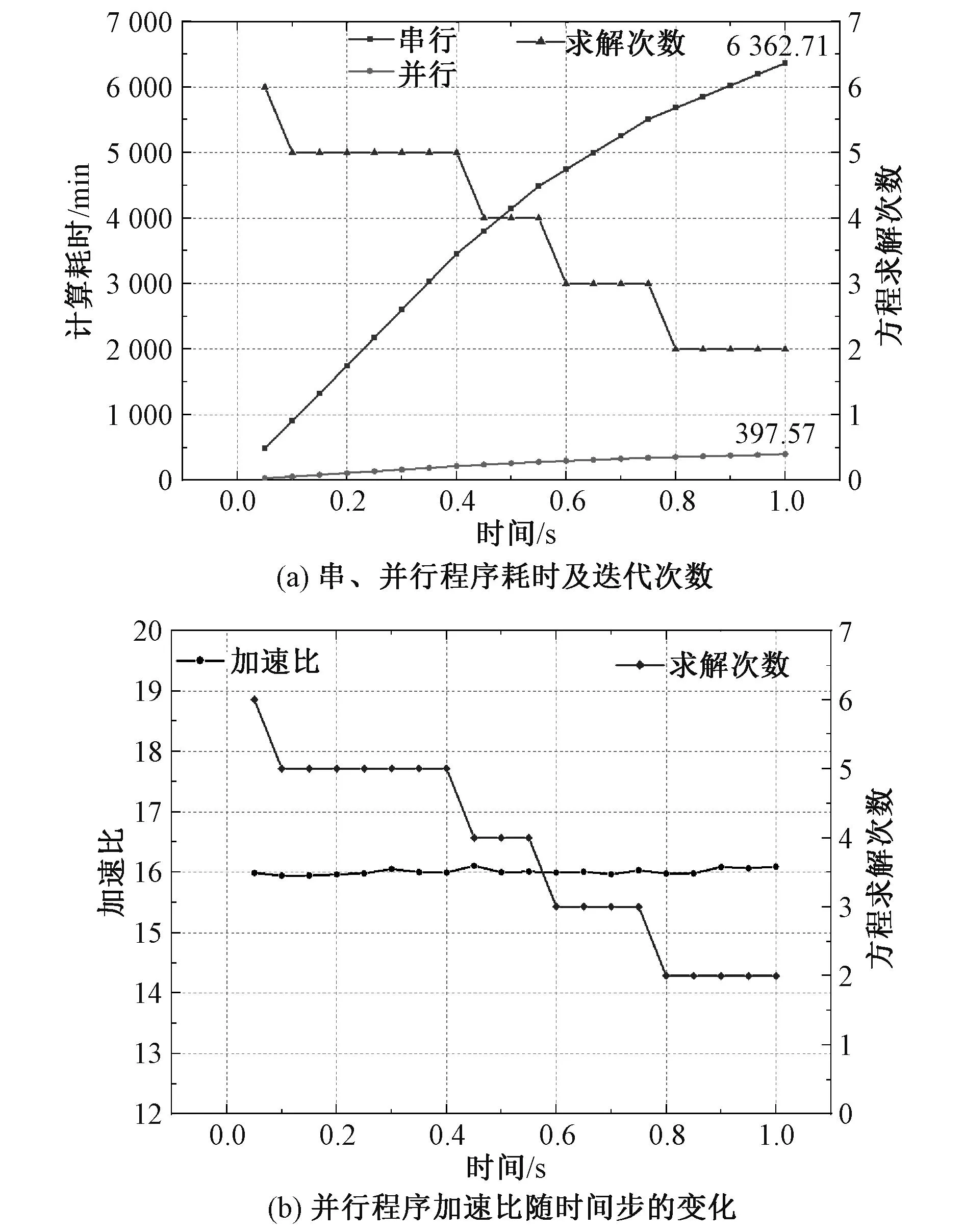
图15 串并行计算效率对比Fig. 15 Comparison of efficiency of serial parallel computing

从图15(a)可以看出,串、并行程序耗时曲线相邻两点之差即为一个时间步内的计算耗时,在计算瞬态流场问题时,串、并行程序每个时间步的耗时与该时间步内方程求解次数有关,一个时间步内求解次数越多,串、并行程序耗时越多,串、并行耗时曲线越陡峭。计算前20个时间步,串行程序的耗时为6 362.71 min,并行为397.57 min,并行程序前20个时间步的加速比为11.277。图15(b)中并行程序加速比定义为串行程序第n个时间步的耗时与并行程序第n个时间步的耗时之比,由图可知,变压器绕组模型并行程序加速比的整体趋势在16倍左右,方程迭代次数对加速比的影响不大,这是因为方程迭代次数多,会增加串行程序耗时的同时也会增加并行程序耗时,且两者的增大趋势一致,从而使得两者的比值,即加速比不受方程迭代次数的影响。

5 结 论

本文采用十字链表法存储有限元刚度阵非零元素,并采用GPU实现了无量纲最小二乘有限元法的瞬态流体场并行计算程序,在验证瞬态并行程序有效性的基础上,分析了大型变压器绕组的瞬态流体场,结论如下:

(1)相较于串行程序,基于GPU加速的并行程序计算耗时大幅度降低,本文采用NVIDIA Quadro P2200对变压器绕组模型二维瞬态流体场计算的并行加速比在16倍左右。

(2)并行程序的加速比与模型的规模有关,与最小二乘有限元程序每个时间步内方程求解次数无关:模型规模越大,并行程序的加速效果越显著;而方程迭代次数只会影响串、并行程序的计算时间,不影响并行程序的加速。