基于多边法的多轴转台相交度测量方法

陈雨婷， 薛 梓， 谢胜龙， 邹 伟， 朱 进， 肖美梁

（1.中国计量大学 机电工程学院， 浙江 杭州 310018； 2.中国计量科学研究院， 北京 100029；3.浙江省计量科学研究院， 浙江 杭州 310018）

0 引 言

多轴转台作为空间角度的发生装置，被广泛应用于飞行器姿态测量、惯性导航测试与校准、精密加工等领域[1]。多轴转台的精度由多个环节的指标精度综合而得，其中回转轴线相交度是其重要的指标。安装、调整多轴转台的过程中会导致各轴之间存在相交误差而不能完全相交，从而影响多轴转台实际测量时的精度，转台转动过程中负载和转速会导致轴线相交度发生变化。转台安装、调试、校准、应用环节对轴线相交度的实时快速测量，有助于提高转台的测量精度[2]。

针对多轴转台轴线相交度的求解问题，众多研究人员提出了测量方法。Zhou J 等使用打表法测量安装于三轴转台上的三维实体棒转动角度并对其调同轴，通过测量三维实体棒得出影响轴线的长度及角度信息[3]；毕超等将三坐标机作为辅助测量仪器，移动转台找到最佳测量位置，测量标定物标定轴线[4]；Guo X T 等采用单站相机测量转台上若干靶标，建立转台坐标系，测量一定范围的靶标位置信息进而计算轴线[5]；仁顺清等采用水平仪测量轴线铅垂度，再用经纬仪观测安装于轴端的靶标，结合细丝引出各轴轴线，得到了五轴转台非整周回转的轴线[6]；于之靖等提出一种基于单CCD 相机多基站测量法，建立了单点多站光线交会模型，通过整周空间点位姿拟合球面获得球心，进一步拟合轴线[7]；鲁亚楠等将多站相机固定于转台上，通过对相机自身标定来测量转台平面[8]；王明元等人采用激光跟踪仪跟踪轴两端靶镜，静态测量整周转动中的若干点，构造两圆并通过连接两圆心获得轴线方程[9]；余佳焕等提出一种室外全站仪跟踪棱镜测量太阳能发电系统装置轴线的方法，对测量点进行平面拟合与球拟合，得到轴线方程，精度在毫米级[10]。

目前相交度测量方法分为接触式测量和非接触式测量两种。接触式测量主要有打表法、细丝法等依靠辅助工件测量的方法，需要考虑工件安装精度且操作繁琐，不适用于实时测量[11-12]。非接触式测量按照测站数量分为单站和多站，常规的单站测量通过长度和角度结合测量被测物的空间位置，测量盲区较大；多站法可以减小测量盲区，以激光跟踪干涉仪为例，仅通过长度量实现目标的位置测量，不需要引入角度，避免了引入角度测量带来的误差，是当前测量精度较高的方法[13-14]。

本文利用多台激光跟踪干涉仪，构建了一个可实时跟踪测量多轴转台转动轨迹的多站测量系统。

1 基于激光测距的转台相交度测量原理

1.1 测量系统参数标定

为获取多轴转台的空间位置，首先采用四路激光跟踪干涉仪（基站）S1、S2、S3、S4组成测量网，构建坐标系，四路是实现系统参数标定的最小单元，标定布局如图1 所示。

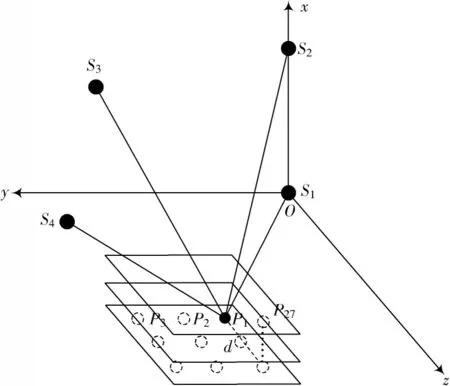
图1 坐标系及参数标定布局

通过标定确定仪器参数（xsn,ysn,zsn），n=1,2,3,4。其中设S1为坐标系原点（0,0,0），S2在x轴上设为（xs2,0,0），S3在xOy平面内设为（xs3,ys3,0），S4为靠近xOy平面的基站，设为（xs4,ys4,zs4）。采用若干动点以及z方向的距离d作为约束进行系统参数和初始点P1位置的标定[15]。在x方向分布的三个平面上均匀选取27 个标定点，4 台激光跟踪干涉仪同时跟踪靶球，通过移动靶球依次获取所有标定点对应的干涉测长值。利用最小二乘原理求解系统参数，为避免迭代出现奇异值，使用Levenberg-Marquardt[16]进行求解。

1.2 双轴转台转动轨迹点测量

双轴转台轴测量示意图如图2 所示。双轴转台具有水平轴与竖直轴（对应卧式转台与立式转台），两者相互的空间关系如图2a）所示，水平轴被测面面向坐标系xOy平面，竖直轴的被测平面与xOy平面近似垂直。系统参数标定后，任意三路或四路基站可实现目标点坐标测量，由于双轴转台的高度与地面基站S4相近，靶球水平放置于竖直轴被测面转动时容易导致S4断光，故采用基站位置较高的S1、S2、S3进行测量。基站和初始点P1的空间坐标均已知，初始点对应的初始长度ln1已知，保持靶球不断光，通过将靶球转移至转台被测面的靶座上跟随转台转动，得到靶球转动轨迹任一动点对应的干涉测长lni，即可得基站测得的目标点相对于初始点的距离变化量Δl。根据距离变化量与初始点坐标，得到每台基站到任一目标点的实际测量距离公式为：

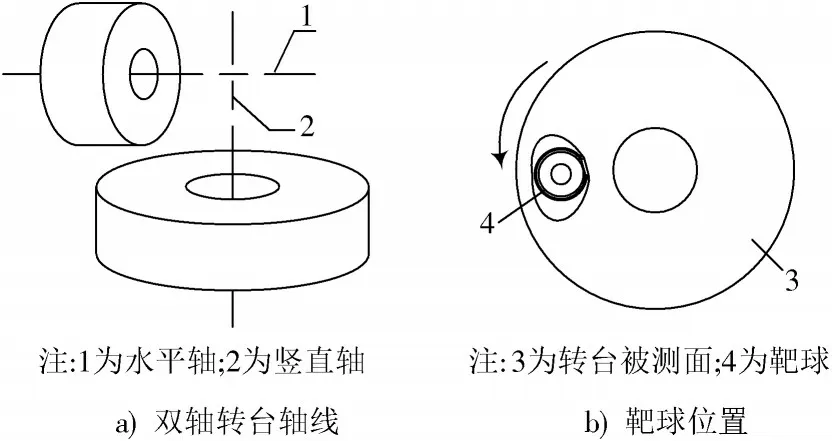
图2 双轴转台轴测量示意图

根据三球交会原理，任意3 台基站测量的目标点在空间中存在正解与负解，均取正解作为目标点的坐标。将基站测量的距离值代入式（2）即可解算目标动点Ti(xi,yi,zi)，i=1,2,…,n的坐标值。

靶球接收光范围为-60°～60°，对于水平轴，基站组成的测量网位于卧式转台被测面一侧，转台转动过程中不存在遮挡现象，可获取完整的转动轨迹点；对于竖直轴，为避免立式转台转动时卧式转台遮挡光路，分段获取转动轨迹点。轨迹点为空间中分布在圆轨迹附近的散点，将散点拟合于平面，得到平面对应的法向量与拟合轨迹的圆心，以此获得回转轴的平均轴线方程。

1.3 回转轴轴线相交度求解

根据1.2 节中动态测量原理，获取轴线的关键在于确定被测平面。为使求解的离散点尽可能在一个平面上，构建不过原点的平面方程：

将离散点代入式（3）表示为矩阵形式：

式中：X为待求平面参数，X=[A,B,C]T；I=[1,1,…,1]，构成超定方程。根据离散数据最小二乘拟合方式，由式（6）求出平面参数。

另外，圆上任意两点连线的中垂线经过圆心M（xc,yc,zc），则两垂直向量关系可用下式表示：

根据平面参数得到竖直轴、水平轴法向量为N1=(a1,b1,c1)、N2= (a2,b2,c2)，两个向量叉乘得到两异面轴线公垂线的向量：

两个拟合圆心M1、M2为水平轴与竖直轴上两点，异面两轴线间最短距离为两圆心向量在公垂线向量方向上的投影，即回转轴线相交度，公式如下：

2 基于激光跟踪干涉仪的多站测量系统的不确定度分析

对于激光跟踪干涉仪测量的目标点坐标以及多轴转台轴线相交度解算结果，影响结果不确定度的因素主要有激光干涉测距误差、坐标系统参数标定引起的测长误差、多光路交会于光学中心不一致造成的测长误差和转台端跳误差。除此之外，存在空气温湿度等环境因素造成的测长误差，因实际实验时在恒温恒湿隔振实验室进行，环境影响较小，故仅研究对测量结果影响较为明显的误差因子。实际应用中使用多台仪器（数量≥3）进行动态测量，本文按照3 台基站（最小测量单元）对测量方法展开分析。

2.1 多站激光干涉测长误差引入的不确定度

由于每个基站位置不同，与被测目标点的距离不同，目标点在空间中移动时每个基站对应的测距并不是同时增大或减小，对于测距误差引入的空间点坐标不确定度无法统一衡量，所以需要通过仿真进行分析。

按照1.2 节中原理在仿真中建立坐标系，选择S1、S2、S3作为测量基站，设置基站坐标真值分别为（0，0，0）、（1 965，0，0）、（1 452，4 132，0）、（-897，4 154，460），初始点P0（-1 300，1 000，3 000），设定测量区域x∈[-1 500，500]，y∈[0，4 000]，z∈[3 000，8 000]，单位为mm，在该区域布置三个方向上的若干散点，如图3 所示。

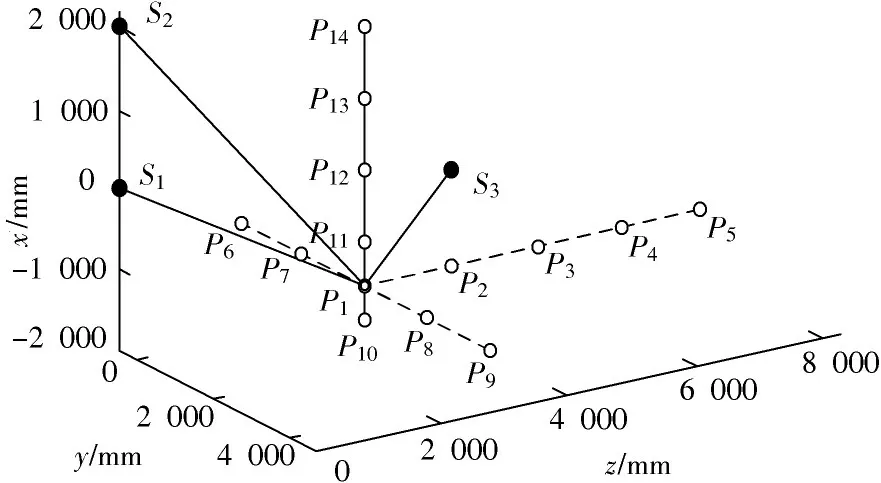
图3 仿真点分布

将每个基站与每个目标点间的距离lni、基站距离初始点的长度ln0作为理论真值的代入量。

基于激光跟踪干涉仪的多边法，依靠长度变化量解算坐标，初始点固定，长度变化量Δl的误差与目标点到测量网的距离有关，且随着距离增加，激光干涉测距带来的误差也在增大，其单站的测距不确定度U=0.2 μm+0.3 μm/m。

为了分析多站激光跟踪干涉测长误差对空间内不同方向上分布的点坐标测量不确定度的影响，将图3 中x、y、z方向上均匀分布的所有三维点作为被测点，对基站与各点之间的距离真值加入[-U,U]之内的随机噪声模拟测量值，进行10 000 次仿真，测量求解所有空间点三维坐标，并对三个方向的每个点进行坐标分量的不确定度计算。被测点在z方向上分布时，即被测点在垂直于测量网的方向上移动，点坐标分量不确定度如图4 所示。随着空间点z值增加，点坐标分量z的不确定度增大趋势较为明显；z值变化对点坐标分量y的不确定度几乎没有影响，对点坐标分量x影响较小，在测量空间内其不确定度不超过0.2 μm。

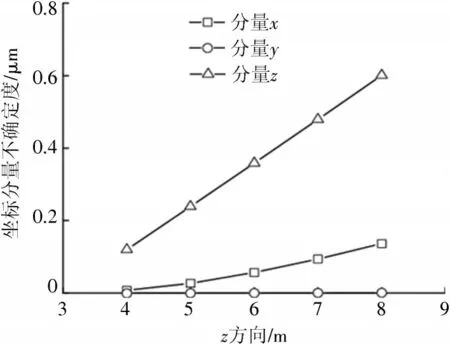
图4 z 方向上不确定度变化规律

被测点在y方向上分布时，即被测点相较于测量网横向移动，点坐标分量不确定度如图5 所示。

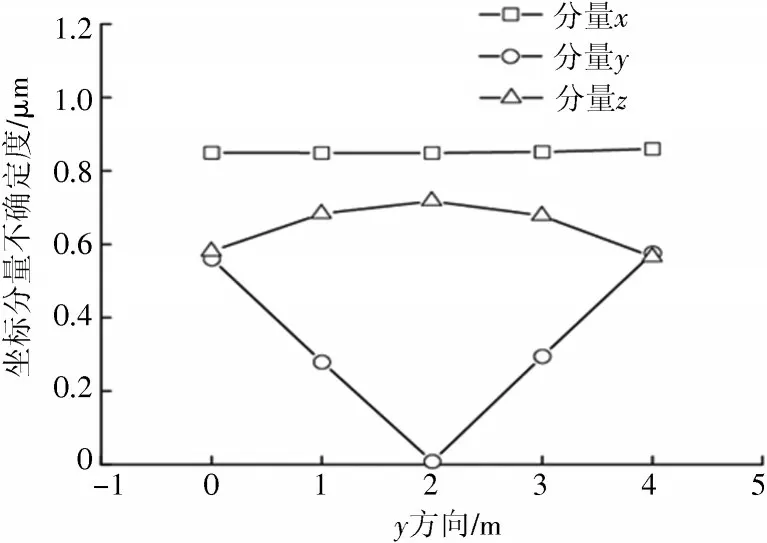
图5 y 方向上不确定度变化规律

由图5 可知：空间点坐标分量x的不确定度变化较为稳定，约为0.85 μm；分量y不确定度在被测点处于中间位置（y=2 m）时最小，对坐标标准不确定度的影响可以忽略不计，向两段移动时逐渐增大。

被测点在x方向上分布时，即被测点相较于测量网纵向移动，点坐标分量不确定度如图6 所示。在测量空间内被测点的高度越接近坐标原点S1，其坐标分量x的不确定度越小，坐标分量z与之相反，坐标分量y的不确定度几乎不受被测点的纵向移动影响，较为稳定。

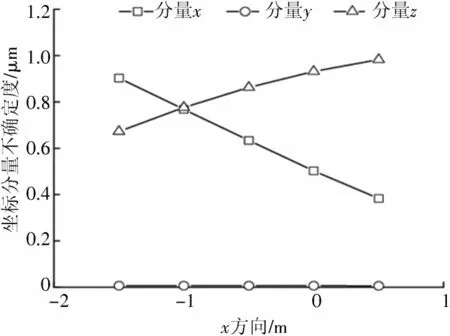
图6 x 方向上不确定度变化规律

经分析，测距误差对空间点坐标分量不确定度的影响在x、y、z方向上分别呈现不同的规律，点坐标分量y的不确定度只有在点坐标y值变化时有明显改变，当被测点为点P8（x=-1 300 mm,y=3 000 mm,z=4 000 mm）时，其坐标分量x、y、z的不确定度为0.85 μm、0.29 μm、0.68 μm，则实际的激光干涉测长误差导致的三维空间点坐标的标准不确定度为：

2.2 系统参数标定误差引入的不确定度

测量目标点坐标之前需先对系统参数进行标定，再对目标进行跟踪测量。系统参数标定是误差的主要来源，根据测量原理式（2）可知，系统参数误差会直接引起目标点的坐标测量误差，导致解算结果出现误差，从而影响目标点测量不确定度。引入标定误差后基站坐标变 为(xe,ye,ze) =[xn+ Δx,yn+ Δy,zn+ Δz]，由 基 站 坐 标偏差引起的测距误差Δd为：

被测点以P8为例，标定的系统参数误差为30 μm时，代入式（14）计算得到基站与空间点间距离的最大误差为23.7 μm，通过仿真判断，参数标定结果的分布服从正态分布，k=3，则以最小测量单元测量时，参数标定引入的三维空间点坐标标准不确定度为：

2.3 多光路交会误差引入的不确定度

理想情况下，激光跟踪干涉仪在跟踪靶球时射入光线从靶球反射镜光学中心返回，多路光交于一点；而实际测量中靶球发生转动，激光跟踪干涉仪的激光随靶球而动并不断调整光路以跟踪靶球球心，因此存在实际测量球心位置误差，进而造成光路光程差[17]，示意图如图7所示，其中虚线光路为理论光路，实线光路为实际光路。

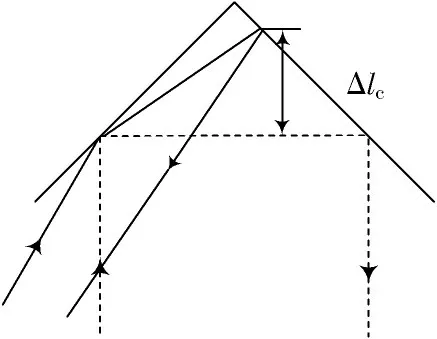
图7 光程差示意图

理论上认为多光路跟踪靶球时对准靶球中心一极小区域内，使得三路光交会于光学中心P，但由于光程差的存在，多路光各自对准靶镜上不同的位置，导致解算的实际交会点P′位于灰色误差区域，如图8 所示。

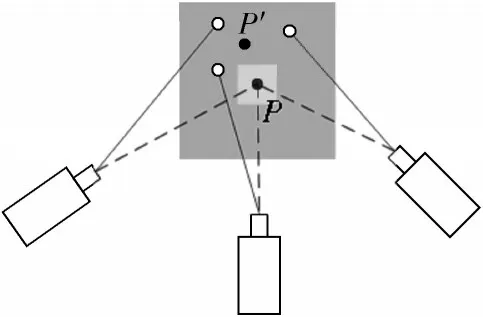
图8 多光路交会误差

多光路实际交会中心与理论光学中心存在误差，靶球光学中心测量误差[18]约为±3 μm，截面圆度误差[19]为±0.2 μm，按照靶球区域内均匀分布考虑，则多光路交会中心引入的三维空间点坐标的标准不确定度为：

2.4 转台端面跳动误差引入的不确定度

转台转动过程中会发生端面跳动，转台自身转动轨迹并非是平滑的，实际测量轨迹点受到端跳影响，拟合圆心位置也随着轨迹点的变动而发生偏移，需要通过拟合计算对轨迹进行一定的修正，对转台存在端跳误差的轨迹进行拟合，分析端跳误差对轨迹圆心的影响。

仿真设定测量空间内生成一段完整的参考圆轨迹，对所有轨迹点加入0～1 μm 的端跳噪声，截取0°～ 90°的弧段，对比不同端跳噪声在拟合后对拟合结果的影响，其中拟合圆半径不确定度在10-9量级，可忽略不计，拟合圆心的坐标不确定度如图9 所示，转台端跳噪声引入的三维空间点坐标的不确定度u4均在10-4μm 级。

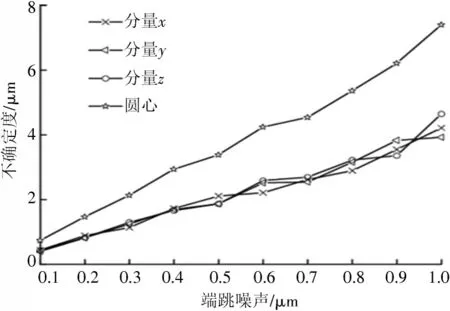
图9 端跳误差引入的不确定度

2.5 空间点测量合成不确定度

由前文分析可知，转台端跳噪声对测量结果的干扰较小，另外3 个主要的系统误差对空间点坐标不确定度影响较为明显，空间点坐标的合成不确定度由3 个主要系统误差引入的不确定度进行合成，因实际测量位置位于图3 中点P8（x=-1 300 mm,y=3 000 mm,z=4 000 mm）附近，故以该点坐标为例，该方法测量的空间点坐标合成不确定度为：

3 双轴转台动态测量实验

为进一步验证测量方法的可行性，设计激光跟踪干涉仪测量轴相交度实验，激光跟踪干涉仪布局如图10所示。

图10 激光跟踪干涉仪布局

3.1 标定结果及干涉测距误差验证实验

测量前按照1.1 节中的方法对测量系统进行参数标定，参考距离d为1 158.514 0 mm，参数标定结果依次为S2（1 964.787 4,0,0）、S3（1 452.330 2,4 132.171 9, 0）、S4（-896.358 9,4 503.933 4, 487.189 5），d=1 158.515 0 mm，参考距离d的标定误差为1 μm。

采用长导轨与一台激光干涉仪对测量系统进行精度验证，长导轨与测量网的径向距离约为6 800 mm，测量装置如图11 所示。

图11 标准距离测量装置

将靶球安装于导轨移动平台的靶座上并使三路激光跟踪干涉仪跟踪靶球，控制导轨使移动平台移动多段标准距离，记录起点和终点时的激光干涉仪示值与三路激光跟踪干涉仪的示值，根据式（2）原理测量每段位移起点和终点的空间坐标，以干涉仪的测量示值作为真值进行对比，比较不同距离下激光跟踪干涉仪的测量误差，3 次实验的测量结果如表1 所示。

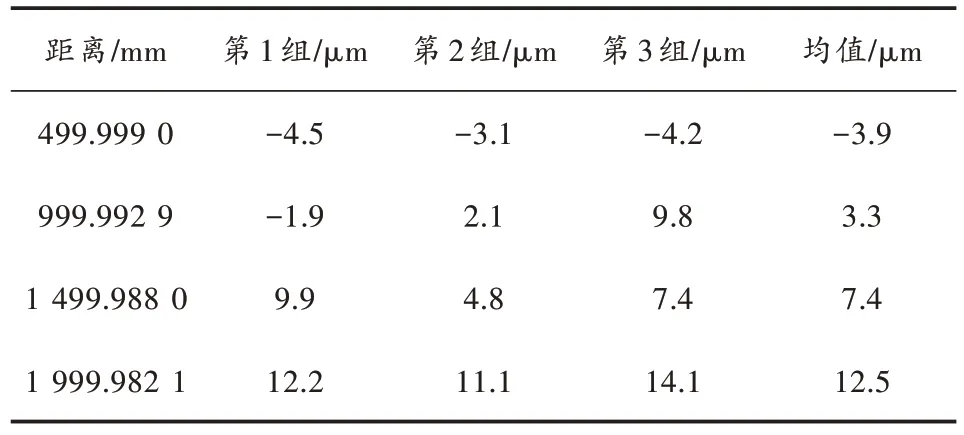
表1 标准距离测量误差

在距离测量网径向距离为6 800 mm 时，三路激光跟踪干涉仪测量横向分布的标准距离最大误差为14.1 μm。常规采用的激光跟踪仪因引入了角度误差，其点位测量不确定度为15 μm+6 μm/m，在此径向距离下跟踪仪的测量误差约为56 μm，本文方法的测量误差显然低于激光跟踪仪测量误差，可满足测量需求。

3.2 双轴转台轴线相交度测量

双轴转台由立式转台（竖直轴）、卧式转台（水平轴）组成，如图12 所示。

图12 双轴转台

靶球安装于竖直轴负载平面时，转台转动导致靶球实际接收光范围小于120°，使靶球边缘尽可能与负载平台呈大约40°，能够保证不断光情况下增大靶球接收光范围，测量步骤如下：

1） 将已接光的靶球放置在初始点固定靶座上，采集3 台激光跟踪干涉仪的初始信息ln0；然后保持光路无阻断情况下，将靶球转移至竖直轴负载平台的固定靶座上。

2） 3 台激光跟踪干涉仪通过同步触发开始测量，水平轴处于锁紧状态，竖直轴从0°起逆时针转动80°，采集靶球轨迹对应的激光跟踪干涉仪长度信息。

3） 竖直轴回到零位，重复测量3 次，完成后保持靶球不断光将其放置于水平轴所在平面。

4） 将转台水平轴所在平面面向基站一侧，竖直轴锁紧，水平轴从0°起转动360°，转速相同，获取靶球轨迹对应的激光跟踪干涉仪长度信息。

5） 将采集的测长信息通过1.2 节中算法进行转动轨迹散点坐标解算，采用前述拟合方法对圆轨迹进行拟合，竖直轴测量结果如表2 所示，水平轴测量结果如表3 所示。

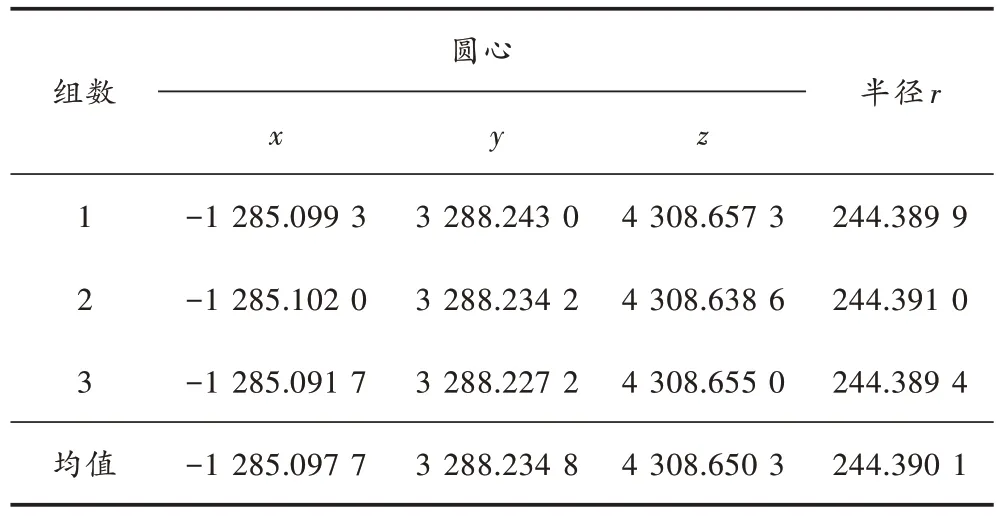
表2 竖直轴转动轨迹拟合结果

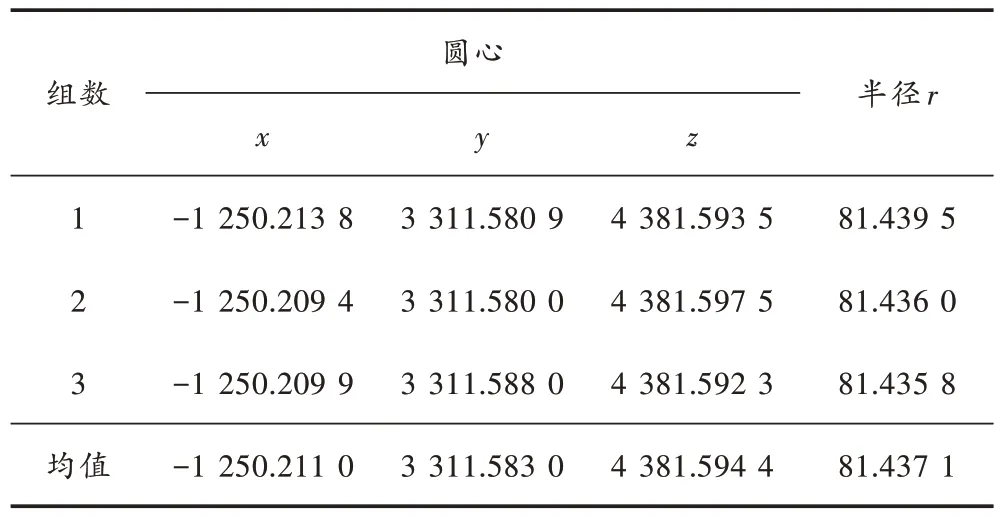
表3 水平轴转动轨迹拟合结果

竖直轴的3 组轴线方向向量分别为[1.000,0.001 8,-0.004 7]、[1.000, 0.001 9, -0.004 8]、[1.000, 0.001 7,-0.004 7]，取均值得[1.000,0.001 8,-0.004 7]，单位为mm。

水平轴的3 组轴线方向向量均为[0.007 2,0.291 9,0.956 4]，单位为mm。获得轴线所过圆心与轴线方向向量的均值后，根据测量原理式（12），可计算本文所采用的方法测量该双轴转台轴相交度为0.904 0 mm。

4 结 语

本文提出一种基于多边法的多轴转台回转轴线相交度测量方法，重点分析了测量方法的主要误差源，并对测量不确定度进行评价。采用长导轨结合激光干涉仪形成不同大小的标准距离以验证该方法的测量精度，并与常规单站法使用的激光跟踪仪进行对比，因其仅依靠长度实现目标的坐标测量，避免了角度误差带来的影响，所以测点误差相比单站法的误差小。该方法比接触式方法操作容易，能够实时测量并获得双轴转台的轴线参数，计算得到双轴转台的轴相交度为0.904 0 mm，减小了传统方法测量的盲区且不受轴数限制，同样适用于其他回转轴的测量，能够达到非接触、快速、高精度的动态测量要求。