面向灰色区间的三支概念分析

孟 茜 ,万仁霞,3* ,苗夺谦 ,赵公杰

（1.北方民族大学数学与信息科学学院，银川，750021；2.同济大学电子与信息工程学院，上海，201804；3.宁夏智能信息与大数据处理重点实验室，北方民族大学数学与信息科学学院，银川，750021）

形式概念分析［1］（Formal Concept Analysis，FCA）是1982 年德国学者Wille 提出的一种有效的知识表示与知识发现的工具，具有层次性和可视化的特点，已被广泛应用于知识工程、机器学习、信息检索、数据挖掘和语义Web 等多个领域［2-5］.在多学科多理论交叉融合的研究趋势下，形式概念分析与其他相关理论的交叉和互补研究使其进一步蓬勃发展，特别是与粗糙集、模糊集、三支决策理论的结合，有效地拓宽了形式概念分析的应用领域.Qi et al［6］基于三支决策理论与经典概念分析提出三支概念分析理论（Three-way Concept Analysis，3WCA），将形式概念二支表达拓宽为三支表达.三支概念一经提出便引起众多学者的广泛关注［7-10］.龙柄翰和徐伟华［11］将三支概念分析融入模糊集合论，提出模糊三支概念分析与模糊三支概念格，对标处理模糊不确定信息，从而实现不确定对象的有效识别和分类.然而，三支概念理论及其推广理论可以处理“非此即彼”的布尔数据，又或是“亦此亦彼”的模糊数据，但对于“范围已知，内部未知”的灰色区间数据的处理却涉及较少，因此本文考虑将灰色系统理论中处理灰色区间信息的方法引入三支概念，以拓展三支概念分析研究的理论背景.

灰色系统理论［12-14］最早由我国数学家邓聚龙提出，其主要理论包括灰色观念、灰色预测、灰色决策和灰色数学等，其中灰色数学是其核心理论之一.在灰色数学中，灰数是指“某个只知道大概范围而不知道确切值的数”，在此基础上，王清印［15］分析并结合模糊集合的表示方法，基于灰数的概念给出灰集合与灰数的描象描述.2005 年Yamaguchi et al［16］将粗糙集理论与灰色数学理论相结合，提出基于灰格的分类提取与约简的决策规则，并定义了灰数运算.随后，Yamaguchi et al［17］针对包含区间数据的信息系统，提出了一种基于灰色系统理论的粗糙集模型.2009 年Wu and Liu［18］在概念格约简的灰色粗集方法中将基于灰数包含关系的灰色粗糙集模型融入到经典形式概念分析中，提出了一种基于灰色粗糙集理论的区间数据形式概念分析方法，将灰色这一概念融入到形式概念分析中.

一方面，由于现实生活中的信息表示的复杂性、不确定性和不精确性等因素，许多观测值常以区间数据的形式存在，如电流、电压等，而灰色数学理论为这些区间数据的处理提供了理论基础；另一方面，三支概念分析突破了经典形式概念中只能表示“共同拥有”的特点，可以同时表示“共同拥有”和“共同不拥有”两个部分，基于三支决策的思想，通过全域、正域和负域的相关运算表达出边界域，使三支概念分析较经典形式概念分析更具有优越性.因此，本文考虑将灰色数学与三支概念分析相结合，基于包含区间值的灰色形式背景提出灰色三支概念，并为解决区间数据的建格问题提供一种可行性方案，拓宽三支概念分析研究的理论支持及实际应用范围.

1 预备知识

1.1 三支概念分析用P(·)表示集合的幂集，用DP(·)表示P(·)×P(·).

定义1［6］一个形式背景K=(U，V，I)由两个集合U和V以及U和V之间的关系I组成，其中U为对象集，V为属性集.若(x，a)∈I（也写作xIa），则表示对象x具有属性a或对象x拥有属性a.

对于X⊆U和A⊆V，定义两对对偶算子分别如下：

正算子*：P(U)到P(V)上的映射和P(V)到P(U)的映射被定义为：

负算子*ˉ：P(U)到P(V)上的映射和P(V)到P(U)的映射被定义为：

其中，Ic=(U×V)-I.

结合正算子*和负算子*ˉ，可以得到以下两对三支算子.

定义2［6］给定一个形式背景K=(U，V，I)，对于X，Y⊆U和A⊆V，一对由属性诱导的三支算子，⊲∶P(V)到DP(U)的映射及⊳∶DP(U)到P(V)的映射定义为：

它们简称为AE算子.

定义3［6］给定一个形式背景K=(U，V，I)，对于X⊆U和A，B⊆V，一对由对象诱导的三支算子，⊲∶P(U)到DP(V)的映射及⊳∶DP(V)到P(U)的映射定义为：

它们简称为OE算子.

定义4［6］给定一个形式背景K=(U，V，I)，对于X，Y⊆U和A⊆V，若有A⊲=(X，Y)且(X，Y)⊳=A，则称((X，Y)，A)为属性导出三支概念，简称AE概念.其中，(X，Y)为AE概念((X，Y)，A)的外延，A为AE概念((X，Y)，A)的内涵.

设((X，Y)，A)和((Z，W)，B)是AE概念，它们的偏序关系定义如下：

若((X，Y)，A)≤((Z，W)，B)，则((X，Y)，A)称为((Z，W)，B)的亚概念，同时((Z，W)，B)称为((X，Y)，A)的超概念.

所有AE概念组成的集合记为AEL(U，V，I)，称为属性导出三支概念格，简称为AE概念格.对于AE概念格，有以下结论.

定理1［6］一个形式背景K=(U，V，I)的AE概念格AEL(U，V，I)是一个完备格，对于任意的((X，Y)，A)，((Z，W)，B)∈AEL(U，V，I)，其上确界和下确界分别为：

其中，∨和∧分别表示上确界和下确界符号，也经常称为并和交.

类似地，也可以定义对象导出三支概念（OE概念）.

定义5［6］给定一个形式背景K=(U，V，I)，对于X⊆U和A，B⊆V，若有X⊲=(A，B)且(A，B)⊳=X，则称(X，(A，B))为对象导出三支概念，简称OE概念.其中，X为OE概念(X，(A，B))的外延，(A，B)为OE概念(X，(A，B))的内涵.

设(X，(A，B))和(Y，(C，D))是OE概念，它们的偏序关系定义如下：

若 (X，(A，B))≤(Y，(C，D))，(X，(A，B))称为(Y，(C，D))的亚概念，同时(Y，(C，D))称为(X，(A，B))的超概念.

由所有OE概念组成的集合记为OEL(U，V，I)，称为对象导出三支概念格，简称OE概念格.对于OE概念格，有以下结论.

定理2［6］一个形式背景K=(U，V，I)的OE概念格OEL(U，V，I)是一个完备格，对于任意的(X，(A，B))，(Y，(C，D))∈OEL(U，V，I)，其上确界和下确界分别为：

1.2 灰数

定义6［17］G是论域U上的灰集合，由上隶属度函数(x)和下隶属度函数(x)两个映射共同定义，如下：

定义10［17］对∀x，y∈R，则其对应的灰数为⊗x和⊗y，灰数的基本运算定义如下：

（1）并运算

（3）补运算

定义11［19］灰度设灰数⊗x产生的背景或论域为Ω，μ(⊗x)为灰数⊗x取数域的测度，则：

称g∘(⊗x)为灰数⊗x的灰度.

2 基于灰色形式背景的三支概念分析

本节将灰数理论与三支概念分析结合，在灰色形式背景下构造灰色三支概念格，用来处理灰色区间数据.

以下用G(·)表示灰集合的幂集，用DG(·)表示G(·)×G(·).

定义12称=(U，V，)为一个灰色形式背景，其中U为所有对象的集合，V为所有属性的集合，是定义在U×V上的灰集合，对于∀(x，a)∈U×V，有(x，a).其中，

注本文中(x，a)表示对象x在a属性上的值的上隶属度和下隶属度，即属性a在对象x上可能存在值的最小值和最大值；(X，a)表示对象子集X在属性a上的共同可能存在值的最小值和最大值；(x，A)表示属性子集A在对象x上共同可能存在值的最小值和最大值；表示(x，a)的灰度，即(x，a)的未知程度；灰数⊗s则表示某对象在某属性上的值的合格灰色区间.

基于灰色形式背景，定义正、负灰色算子如下.

定义13给定一个灰色形式背景=(U，V，)以及灰数⊗s，X⊆U，A⊆V，γ(X)和γ(A)分别为X与A上的灰度组成的集合，则灰色正算子⊗*：G(U)到G(V)上的映射和G(V)到G(U)的映射定义为：

它们称为灰色AE算子.

定义15给定一个灰色形式背景=(U，V，)，对于X⊆U和A，B⊆V，一对由对象诱导的三支算子，⊲∶G(U)到DG(V)的映射及⊳∶DG(V)到G(U)的映射定义为：

它们称为灰色OE算子.

下面为灰色AE概念和灰色OE概念的定义.

定义16给定一个灰色形式背景=(U，V，)以及灰数⊗s，X，Y⊆U，A⊆V，记：

若X⊲=(γ(A),γ(B))，且(γ(A),γ(B))⊳=X.则称(X，(γ(A)，γ(B)))为对象导出灰色三支概念，简称GYOE概念.其中，X叫作GYOE概念的外延，(γ(A)，γ(B))叫作GYOE概念的内涵.

命题1给定一个灰色形式背景=(U，V，)以及灰数⊗s，X，X1，X2，X3，X4⊆U为对象子集，A，A1，A2，A3，A4⊆V为属性子集，则下列结论成立：

同理可证X⊆X⊲⊳.

（3）由命题（2）可知A⊲⊆A⊲⊳⊲，再由命题（1）知A⊆A⊲⊳，得A⊲⊳⊲⊆A⊲，故A⊲=A⊲⊳⊲得证.

同理可证X⊲=X⊲⊳⊲.

（4）因为有：

由命题（1）得：

因此，

同理可证：

故证得：

同理可证：

由命题（1）得：

故命题（5）得证.

同理可证：

（6）令(γ(X1)，γ(X2))=A⊲，由命题（2）可知A⊲⊆A⊲⊳⊲.

又因为：

命题（6）可证.

同理可证：

（7）由命题（6）可知：

再由命题（5）可知：

可证.

同理可证：

由命题（4）知：

同理可证：

定义18设=(U，V，)为灰色形式背景，AEGL(U，V，) 表示由灰色形式背景=(U，V，)生成的所有GYAE概念的集合.

对任意：

定义其偏序关系如下：

定理3设=(U，V，)为灰色形式背景，AEGL(U，V，) 表示由灰色形式背景=(U，V，) 生成的所有GYAE概念的集合，则AEGL(U，V，在偏序关系≤下是一个完备格，称灰色AE概念格，简称GYAE概念格.

对任意：

其下确界和上确界分别为：

证明由于上确界与下确界证明类似，这里只证明下确界.因为，

由命题（3）得：

再由定义18 得：

为一个下界.

定义19设=(U，V，)为灰色形式背景，OEGL(U，V) 表示由灰色形式背景=(U，V，)生成的所有GYOE概念的集合.

对任意：

定义其偏序关系如下：

定理4设=(U，V，)为灰色形式背景，OEGL(U，V，) 表示由灰色形式背景=(U，V，) 生成的所有GYOE概念的集合，则OEGL(U，V，)在偏序关系≤下是一个完备格，称灰色OE概念格，简称GYOE概念格.

对任意：

其下确界和上确界分别为：

其证明同定理3 类似.

3 实例分析

例1给定一个灰色形式背景=(U，V，)，其中，U={x1，x2，x3，x4}表示供货商备选集合，V={a，b，c}表示供应商的产品质量、产品价格及运送时间三个属性(x，a)表示某个供应商某个属性的普遍评价区间，且(x，a)区间在[0，1]范围之内，如表1 所示，取⊗s=[0.6，1]为合格区间.

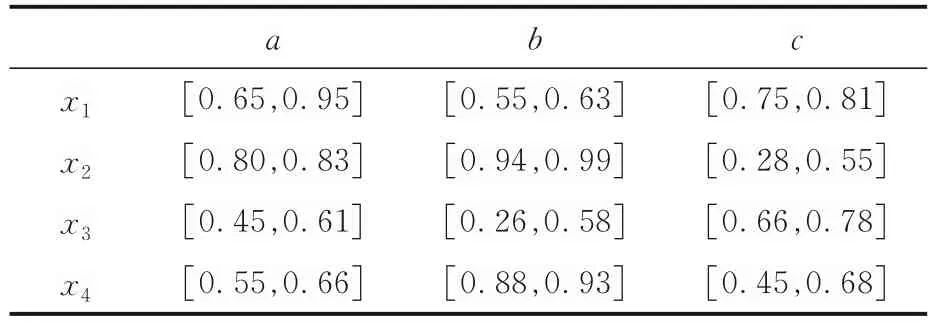
表1 灰色形式背景Table 1 A grey context

对于∀(x，a)∈U×V，(x，a)在[0，1]，根据定义11，此时μ(Ω)=1，则本示例分析中灰度计算如下：

由表1 可得属性导出灰色三支概念的外延与内涵（表2）以及对应的GYAE概念格（图1）.从AE5可以看出，同时具备a和b属性合格的是x2，且合格的共同评价区间为∅，故灰度为0，而a和b属性同时不合格的是x3，且未能合格的共同评价区间为[0.45，0.58]，则灰度为0.13，表明供应商2 号在产品质量和产品价格方面评价较好，且并未有重合部分，供应商3 号在这两方面普遍评价较差，未能合格，且重合部分的灰度为0.13.

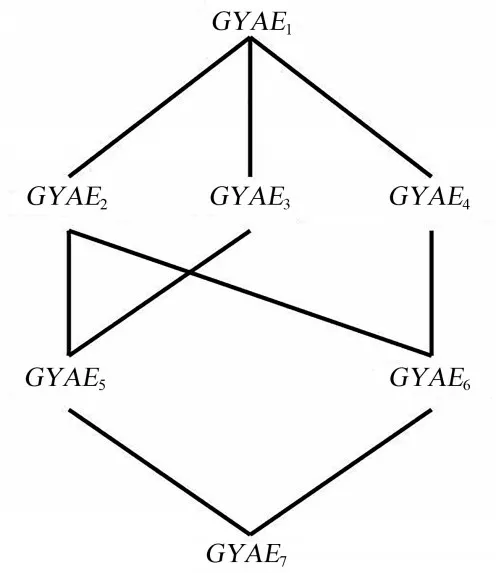
图1 GYAE 概念格Fig.1 GYAE concept lattice

表2 属性导出灰色三支概念的外延与内涵Table 2 The extension and intension of grey three-way concept induced by attributes

对偶地，根据表1 可得对象导出灰色三支概念的外延与内涵（表3）以及对应的GYOE概念格（图2）.其中，从OE8可以看出x2和x4的b属性同时合格，且合格共同评价区间为∅，因此灰度为0；x2和x4的c属性同时不合格，且评价区间为[0.45，0.55]，则此时灰度为0.1.因此，表示供应商2 号和供应商3 号在产品价格方面评价较好，且评价区间并未重合，在运送时间方面评价较差，未能合格，且重合部分的评价灰度为0.1.

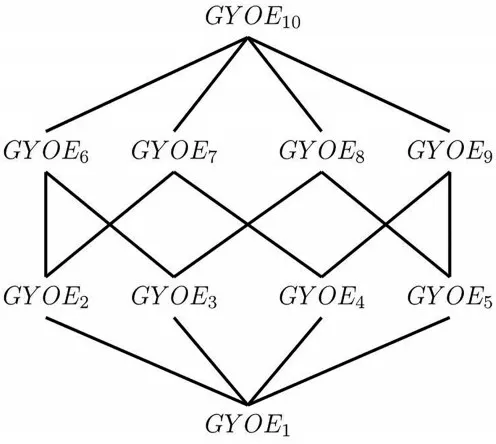
图2 GYOE 概念格Fig.2 GYOE concept lattice

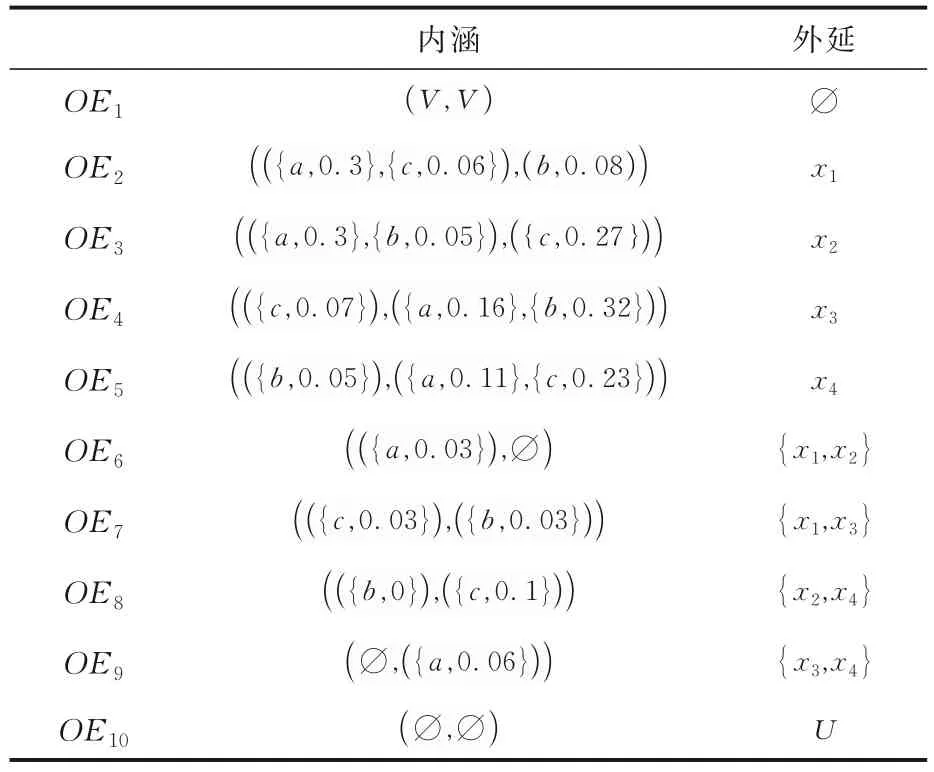
表3 对象导出灰色三支概念的外延与内涵Table 3 The extension and intension of grey three-way concept induced by objects

通过上述实例的概念格图，可以直观地看出各供应商所具备的属性、评价区间以及各概念的结构关系.

4 结论

在现实生活的信息系统中，数据的类型不仅包括“非此即彼”的布尔数据、“亦此亦彼”的模糊数据，还包括一些“范围已知，内部未知”的灰色区间数据，而以往的概念格信息处理中鲜有涉及这类数据.本文将灰度和灰格运算融入三支概念分析，提出灰色三支概念及灰色三支概念格，给出了灰色三支的正负算子、灰色三支概念的相关定义、定理及其性质，并通过实例说明灰色三支概念和灰色三支概念格的实用性.一方面可以将得出的结论清晰地表示在图中，另一方面也通过灰度展示灰色信息的未知程度，为分析灰色区间数据提供一种合理的方法.

本文实例中的(x4，a)=[0.55.0.66]，故(x4，a)属于合格区间⊗s=[0.6，1]的可能性较大，实例则将其直接归入不合格区间，虽然杜绝了所有不合格数据归入合格区间，但还需进一步考虑将这些“中间数据”进行更合理地分类.下一步将考虑结合变精度的相关概念，进一步优化灰色三支概念分析理论.