基于改进Stacking与误差修正的短期太阳辐照度预测

王珊珊 吴霓 何嘉文 朱威

太阳辐照度;光伏发电;Stacking算法;回归预测算法;交叉验证

0 引言

太阳能因其典型的波动性与间歇性[1],造成光伏发电系统输出功率的不稳定性,对光伏发电并网与电网的安全稳定运行构成巨大挑战[2-3],同时也阻碍了大规模光伏发电并网．在光伏功率预测的众多影响因素中,太阳辐照度的影响是最直接、最显著的,因此准确的辐照度预测能够提高光伏发电系统输出功率的预测精度,有着重要的理论与应用价值[4]．

近年来,随着机器学习技术的兴起,国内外许多学者将以SVR(Support Vector Regression)[5]、神经网络和随机森林为代表的机器学习算法用于辐照度预测问题中[6-8]．文献[9]通过对9项气象参数的不同组合作为输入,对模型的预测精度进行分析,提出一种基于非线性自回归神经网络的辐照度预测模型,有效提高了预测精度．文献[10]利用EMD(Empirical Mode Decomposition,EMD)和LMD(Local Mean Decomposition)将原始数据分解为多个分量序列,然后对各分量分别进行LSSVM(Least Square Support Vector Machine)预测,最后将各分量的预测结果进行叠加得到最终预测值,相比LSSVM单独预测,精度有了明显提升．单一的预测模型都是对特定假设空间进行预测,所以用单一模型来预测辐照度不可避免会存在预测误差．而集成模型相比单一模型能够集成多个模型的不同特点,对各个模型取长补短,从而提高预测性能,Stacking模型便是目前最热门的集成模型之一．文献[11]通过构建一种基于同质SVM(Support Vector Machine)弱学习器的Stacking模型,得到了比单一模型更精确的预测效果．文献[12]提出一种新的向量表示法来稳定模型数据维度,并根据预测精度来调整Stacking基模型赋权,减少了输出的噪声和时间开销．目前大多研究专注于提升预测模型的精度来提高辐照度预测效果,却忽略了模型的预测误差中也存在非常多的有用信息,这导致现有研究难以进一步提升短期辐照度预测的准确度．

为了解决以上问题,本文提出一种基于改进Stacking集成学习与误差修正的短期辐照度预测模型．在数据优化层面,利用梯度提升决策树(Gradient Boosting Decision Tree,GBDT)模型计算辐照度数据集各分量的重要度并排序,清除其中的冗余特征,提高预测精度和运算效率．在算法创新方面,预测模型采用Stacking集成模型将4种差异性较大的算法融合,通过异质集成得到优于个体学习器的预测精度和泛化能力．针对Stacking模型平均处理测试集预测结果而带来的掩盖学习器优劣的问题,提出对初级层的输出根据各模型的预测精度进行加权处理．同时,将Box-Cox变换嵌入Stacking,此举可有效提高数据的正态性、可加性和同方差性．在误差修正层面,针对Stacking模型的预测误差构建了基于随机森林(Random Forest,RF)的辐照度误差预测模型,并最终将改进Stacking模型的预测结果与辐照度误差预测结果进行叠加以获得最终预测结果．实验结果表明,该集成模型具有优于单一模型和传统Stacking模型的预测精度．

1 相关理论和方法

1.1 GBDT算法

GBDT是一种由多个弱学习器组成的迭代决策树算法．该方法利用梯度增强算法来最小化损失函数,达到逼近真实值的目的,具有灵活性高、鲁棒性强、预测精度高等特点．

将GBDT应用到特征重要度计算中,通过对决策树中分裂节点增益进行计算并积累求和,从而对某个特征进行重要度评价．其中,特征j的全局重要性是以特征重要度平均值来度量的,其计算公式为

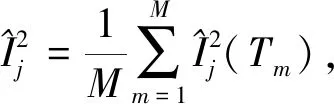
(1)

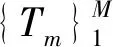
(2)

1.2 RF随机森林

随机森林[13]是一种基于决策树的集成式机器学习算法,它在每一棵回归树建立随机采样样本空间与特征空间,随机属性的引入减少了回归树模型间的相关关系,通过结合大量回归树来提高模型泛化能力,从而使算法具有效率高、精度高的特点．

1.3 Box-Cox变换

Box-Cox变换是一种基于极大似然估计的数据变换技术,计算过程简单且无需先验信息,能够有效提升观测的同方差性、正态性和可加性[14]．

Box-Cox变换一般形式如下:

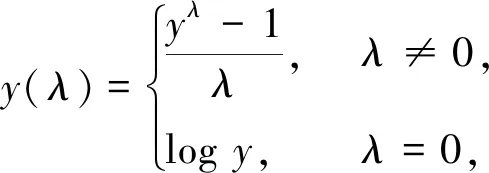
(3)

式中,λ为变换参数,y为原始因变量,y(λ)为新变量,Box-Cox逆变换为

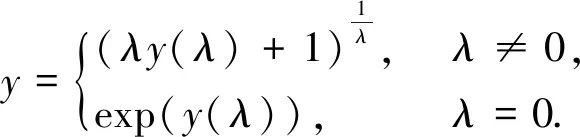
(4)

参数λ采用最大似然估计进行计算,构造似然函数L*(λ)如下:

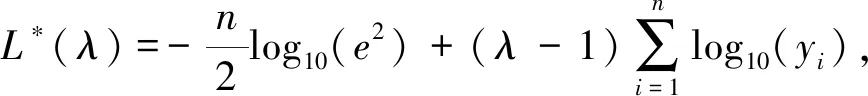
(5)

式中,n表示采样次数,e2表示y(λ)方差的极大似然估计值,通过式(5)求解出使得L*(λ)取最大值的最优λ,利用该参数进行Box-Cox变换可以很大程度上提升数据的正态性和数据间的相关性．

1.4 其他模型

1)K最邻近算法(KNN)原理

K最邻近算法(k-Nearest Neighbor,KNN)作为一种经典的机器学习算法在理论上十分完善,具有算法简单、容易实现、训练效率高、对异常值不敏感等特点．该算法核心思想是对不同特征值之间的距离进行度量,通常采用欧式距离和曼哈顿距离．

2)XGBoost算法

XGBoost(eXtreme Gradient Boosting)算法是基于GBDT算法改进而来的,它通过增加正则项控制模型计算复杂度,并利用二阶泰勒展开式并行计算特征分裂增益以提高模型预测精度、减少计算时间．

3)支持向量回归机(SVR)原理

支持向量机应用于回归问题形成了SVR,输入向量按照既定非线性映射映射至高维特征空间进行线性回归以获得空间内非线性回归的效果．在回归运算时,将不敏感损失函数引入到构造中,以搜索到最优的分类面使得训练样本和该分类面之间的综合误差达到最小值．支持向量回归在小样本、高维、复杂数据上进行非线性回归预测时展现出了优异的性能．

4)岭回归原理

岭回归(Ridge Regression)是一种正则化方法,通过舍弃最小二乘的无偏性和部分精确度,获得了效果更好且回归系数更符合实际的回归过程．岭回归通过对损失函数增加惩罚项以控制线性模型复杂程度,增强了模型的稳健性．

2 基于Box-Cox变换的改进Stacking短期辐照度预测方法

2.1 Stacking集成学习模型

Stacking算法是一种分层集成的方法．不同于Bagging和Boosting算法整合同类型模型,Stacking算法能够集成异质模型[15]．在 Stacking 集成模型(图1)的训练过程中,通常使用K折交叉验证法来划分数据集和进行模型训练,以减少过拟合的风险．首先将原始数据集以8∶2的比例划分为训练集和测试集,接着将训练集等分地划分为k个子集,分别选择其中k-1个子集的并集作为训练集,余下的1个子集作为验证集,由此可获得k组训练集和验证集．对每个基模型都采用这k组训练集和验证集进行学习器的训练和验证,并将预测结果配合样本真实值标签构造为新的训练集输入第二层元学习器训练,最终得到的预测结果即为Stacking模型的最终预测结果．Stacking算法最突出的优势是集不同模型之长,能够对原始数据进行多角度的分析,使得模型获得相比基模型更好的预测性能．所以基学习器应选择性能优越且原理各异的模型,元学习器则应选择泛化能力强的算法,以融合各基学习器预测的优点,达到最优的预测效果．本文选择 SVR、XGBoost、KNN、岭回归作为基学习器,元学习器则使用泛化能力较强的岭回归算法．

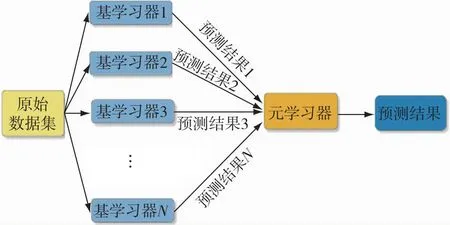
图1 Stacking模型结构Fig.1 Stacking model structure

2.2 改进Stacking

2.2.1 基于GBDT算法的特征筛选

利用GBDT对辐照度数据进行特征选择,对各个特征进行重要度排序．各特征与实际辐照度之间的相关系数如表1所示．由表1的相关系数数据,剔除掉风向、气压2个相关性弱的特征,最终选择温度、时刻、风速、湿度作为模型输入,降低计算复杂度,提升模型训练效率．

表1 相关系数

2.2.2 基模型赋权与Box-Cox变换

Stacking算法中元学习器输入向量来自基学习器的输出,使得训练数据被各层学习器重复学习,造成模型的严重过拟合．因而需要在模型建立前对数据进行交叉验证划分,提升模型的泛化能力[16]．如果训练得到的基学习器模型预测效果比较好,那么该模型的预测结果也会更接近真实值．但传统的Stacking模型初级层对测试集预测结果的处理方式为直接平均处理,使得优秀模型的优越性被其他模型掩盖．同理,效果较差的模型也会因与其他模型平均而掩盖其预测性能的不足．因此,本文针对同一基学习器在每折上训练得到的不同预测模型,依据其验证集预测值和真实值之间的误差求得权值,再给测试集对同一种基模型的不同预测结果赋权．设学习器所训练出的模型预测误差为eit(i=1,…,k),以此误差在e1t,e2t,…,ekt精度总和中所占比例来分别确定权值ρ1,ρ2,…,ρk,然后对测试集的输出结果赋权,可以使精度更高的预测模型发挥其优越性,增大其对最终结果的影响,并降低精度较低的模型对最终输出的影响．

针对数据特征与辐照度数值相关程度不高的问题,本文对第一层输入第二层的训练集进行Box-Cox变换处理,此举可提高训练集的正态性和可预测性,提升各个特征与辐照度数据的内在联系,进一步减小预测误差．经过Box-Cox变换后的训练集输入元学习器,训练完成后用此学习器输入经加权处理后的测试集进行预测,得到预测结果．精度加权改进和Box-Cox预处理流程如图2所示．

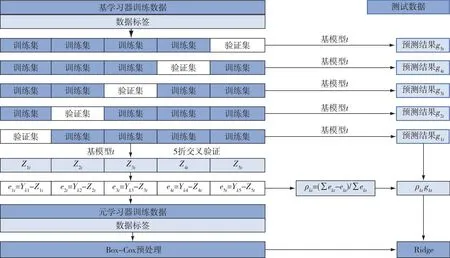
图2 精度加权改进和Box-Cox预处理Fig.2 Accuracy-weighted improvement and Box-Cox preprocessing

精度加权和Box-Cox改进后的Stacking预测模型的流程如算法1所示.

2.2.3 基于RF模型的误差修正方法

通过RF模型来寻找辐照度预测系统误差的变化规律,有助于发现提高模型效果的有益规律,达到提升预测精度的目的．

辐照度预测误差:

e=p′-p,

(6)

式中,e表示辐照度预测误差,p′表示辐照度预测值,p表示辐照度真实值．

算法1:基于Box-Cox的改进Stacking模型Input:训练集 D={(x1,y1),(x2,y2),…,(xk,yk)}1for t=1,2,…,T do2for i=1,2,…,k do3第零层第t个同质基学习器k次训练学习:{Zit=ht(xm,ym),i=1,…,k,t=1,…,T}→{Z1t,Z2t,…,Zkt}4第零层第T个异质基学习器学习训练并构成新的数据样本:{Zit=ht(xm,ym),i=1,…,k,t=1,…,T}→{(Z11,Zk1),…,(Z1Tt,…,ZkT)}5构成新的数据据样本:Dnew={((Z11,…,Zk1),…,(Z1T,…,ZkT),ym)}6对新数据样本作Box-Cox变换处理后输入第一层7第一层预测算法δ训练得到模型:H=δ((Z11,…,Zk1),…,(Z1T,…,ZkT))8计算第零层同质基学习器的误差:{[(y1,y2,…,yk),…,(y1,y2,…,yk)]-[(Z11,Z21,…,Zk1),…,(Z1T,Z2T,…,ZkT)]}=9{[(e11,e21,…,ek1),…,(e1T,e2T,…,ekT)]}10权重计算:ρ11=(e21+…+ek1)/(e11+e21+…+ek1)︙ρk1=(e11+…+ek-1,1)/(e11+e21+…+ek1)︙ρkT=(e1T+…+ek-1,T)/(e1T+e2T+…+ekT)11对第零层测试集数据输出进行权重分配:(ρ11g11,ρ21g21,…,ρk1gk1)(ρ12g12,ρ22g22,…,ρk2gk2)︙(ρ1Tg1T,ρ2Tg2T,…,ρkTgkT)12end13end

计算辐照度初步预测值p′与实际值p误差e,将其作为校正因子,将辐照度校正的补偿值e添加到预测值p′中,获得校正后的辐照度预测值．

2.2.4 改进Stacking模型总体流程

基于上述的GBDT算法、基模型赋权与Box-Cox变换、RF误差修正,本文搭建了短期辐照度预测模型,如图3所示．

图3 基于改进Stacking与误差修正预测模型流程Fig.3 Prediction process based on improved Stacking with error correction

具体思路如下:

1)利用GBDT算法对辐照度原始数据进行特征筛选,去除掉相关程度较低的冗余特征后,其余数据输入改进Stacking模型．

2)采用XGboost、SVR、岭回归、KNN作为Stacking的基学习器,岭回归作为元学习器．对于同一基学习器用不同样本进行训练,基学习器训练出的模型对验证集的预测误差为eit(i=1,…,k),以此误差在e1t,e2t,…,ekt精度总和之中所占比值来确定权值ρ1,ρ2,…,ρk,然后对第一层输入第二层测试集的输出结果进行赋权．

3)对第一层输入第二层的训练集进行Box-Cox变换来提高训练集的正态性和可预测性．

4)经过Box-Cox变换处理的训练集输入元学习器,训练完毕之后,用此学习器对加权过后的测试集进行预测,得到预测结果．

5)采用上述模型进行初步预测后,将初步预测的误差数据输入RF模型中训练,由此获得误差分布模型．将初步预测结果与误差预测值进行叠加得到最终预测结果．RF误差修正模型可以有效弥补初步预测模型本身存在的误差,进一步提高预测的准确度．

3 算例分析

3.1 数据选取

为验证本文模型对于短期辐照度预测的有效性,将中国北方某光伏电站作为具体研究对象．选取2017年2月1日至2018年1月31日的辐照度数据作为原始数据集,共2 920个样本数据．辐照度数值采用太阳总辐射量,采样间隔为3 h,每日采样8个点,包括地表太阳辐照度和风速、风向、温度、湿度、气压共5项观测指标．将数据集按8∶2划分,前80%的数据作为训练集,后20%数据作为测试集,进行回归预测．

3.2 模型评价指标

本文选取均方根误差(ERMSE)、平均绝对误差(EMAE)和决定系数(R2)作为辐照度预测模型的效果评价指标,其中:R2用来检验模型的拟合度,R2越大表明模型拟合程度越好;MAE、RMSE则用来检验预测模型的精度,它们值越小说明精度越高．具体的计算公式如下:

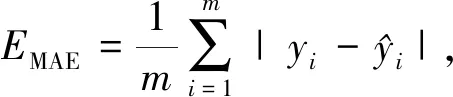
(7)

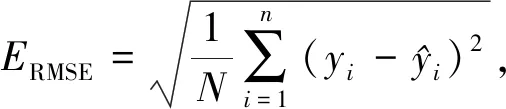
(8)

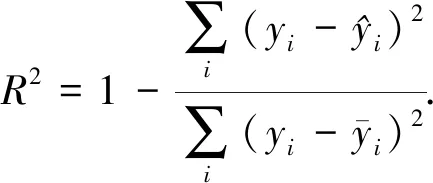
(9)

3.3 仿真实验及结果分析

首先,设计第一组实验,对比Stacking模型与其各个基模型在辐照度短期预测上的性能,各模型预测值与辐照度实际值的横向对比结果如图4所示,各模型的绝对误差如图5所示,各模型的评价指标值如表2所示．

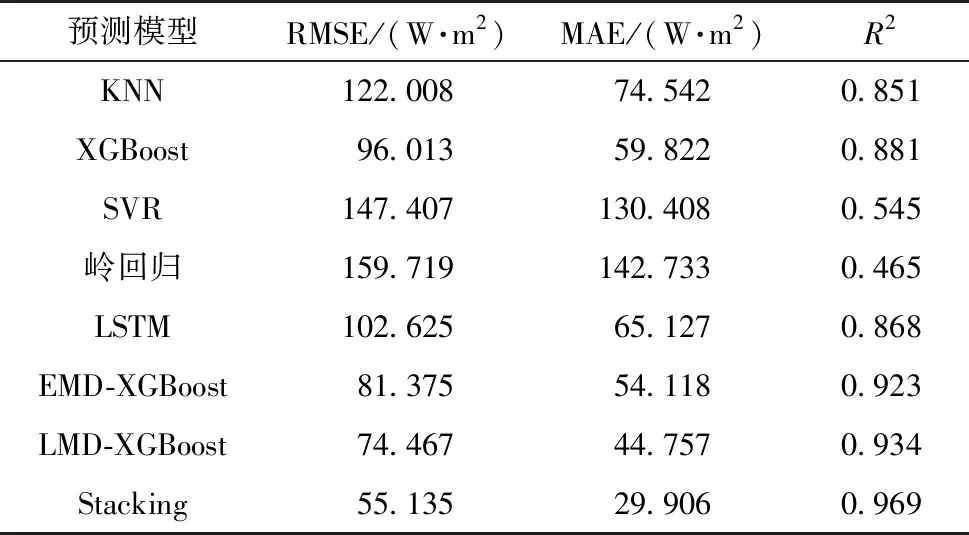
表2 不同模型的评价指标

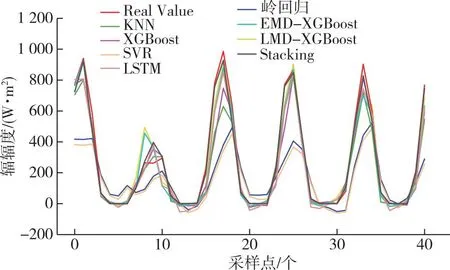
图4 不同模型预测结果对比Fig.4 Prediction result comparison between Stacking method and traditional models

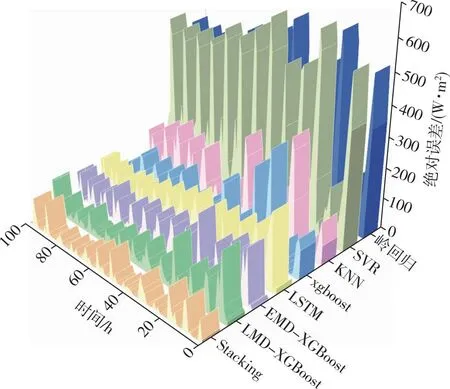
图5 不同模型的预测误差对比Fig.5 Prediction error comparison between Stacking method and traditional models

由图4、5和表2分析可知:Stacking模型相较于其基模型中的单一模型KNN、SVR和岭回归,R2分别提升0.118、0.424和0.504,与深度学习模型LSTM相比,R2指标提升0.101;将EMD和LMD分解与集成模型XGBoost结合后,R2分别达到0.923和0.934,与XGBoost直接预测相比分别提升0.042和0.053,但仍低于Stacking的0.969．因此,相较于其他传统机器学习、深度学习方法和集成学习模型XGBoost,Stacking模型在太阳辐照度的短期预测上有着更高的精度,拟合能力更强．

为了显示本文模型的优越性和各改进点的有效性,搭建了以下4种Stacking对比模型:

1)模型1:经典Stacking模型(Stacking)．

2)模型2:对传统Stacking模型进行GBDT特征筛选的模型(GBDT-Stacking)．

3)模型3:对传统Stacking模型预测结果使用RF算法进行误差修正(Stacking-RF)．

4)模型4:对传统Stacking模型进行权重分配与Box-Cox处理的模型(赋权Stacking)．

由此设计了消融实验来分析各个改进点对Stacking模型预测性能的影响,并将各模型的预测结果与辐照度实际值进行横向对比,结果如图6所示,各消融实验模型的绝对误差如图7所示,消融实验模型的评价指标值如表3所示．

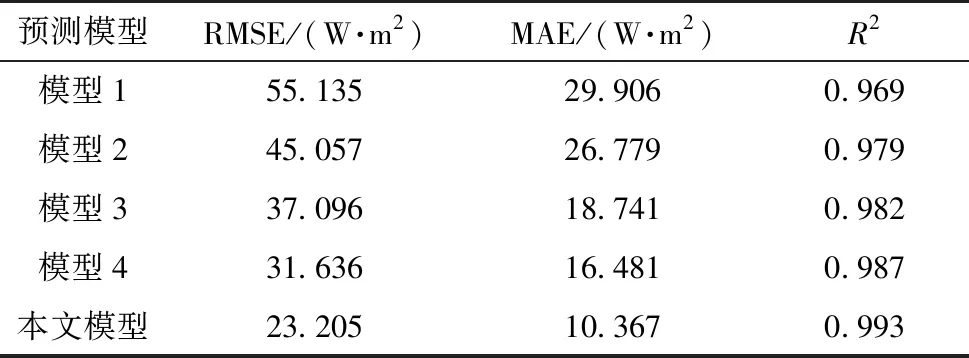
表3 不同模型的评价指标

图6 对比模型与本文所提模型的预测结果Fig.6 Prediction result comparison between the proposed method and classic or modified Stacking models

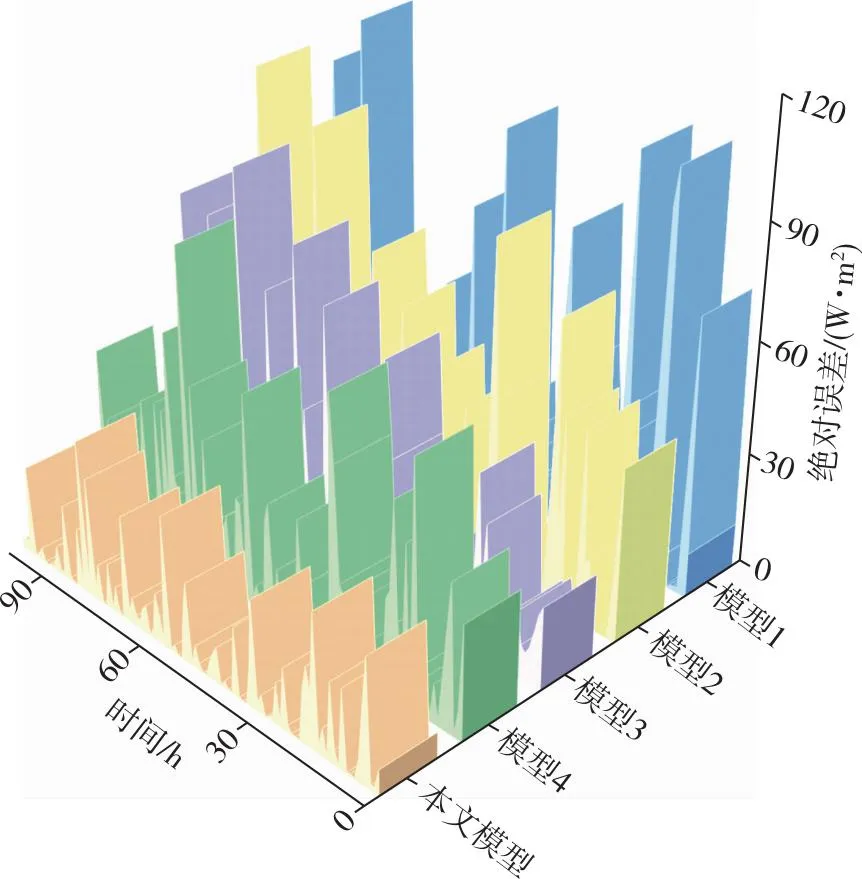
图7 对比模型与本文所提模型预测误差Fig.7 Prediction error comparison between the proposed method and classic or modified Stacking models

由表3可知:本文模型相较于Stacking、GBDT-Stacking、Stacking-RF及赋权Stacking模型,R2分别提升0.024、0.014、0.011和0.006,MAE分别降低65.3%、61.3%、44.7%和37.1%．另外还可以看出:模型4相较于拥有相同学习器的模型1预测效果提升明显且误差波动较小;模型2和模型3也可显著提升Stacking集成模型的预测精度,其MAE分别降低10.4%和37.3%．因此,本文模型能准确预估不同时期的辐照度变化趋势,预测准确度较Stacking模型有较大提升．

4 结语

本文将基于Box-Cox变换和权值分配的改进Stacking模型应用于短期辐照度预测领域,使用4种相互异质的算法作为学习器,充分利用各算法在数据特征结构与特征空间上的不同视角,从而使Stacking集成模型的优越性得以充分发挥．同时,采用GBDT算法进行特征选取和RF算法对误差进行修正,达到了简化计算复杂度和提升辐照度预测精度的目的．实验结果表明:

1)通过对数据进行特征重要度分析,筛选掉相关度较弱的特征,达到了过滤冗余特征,构造出效率精度更高、复杂度更低的独立预测模型的目的．

2)引入误差修正算法计算拟合Stacking集成模型预测结果的动态误差,获得余项预测值,通过加法模型融合预测值与余项得到最终辐照度预测值．结果表明,通过将余项融合进预测结果能降低预测误差．

3)通过与单一预测模型以及传统Stacking模型相比,表明本文所提出的改进Stacking模型具有良好的稳定性和较高的预测精度．